TO CONSTRUCT SOLUTIONS OF THE DIMENSIONALLY REDUCED VARIABLE-COEFFICIENT B-TYPE KADOMTSEV-PETVIASHVILI EQUATION

ZHANG Yan-ni,PANG Jing

(College of Science,Inner Mongolia University of Technology,Hohhot 010051,China)

Abstract:In this paper,we investigate a generalized(3+1)-dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation in fluid dynamics.Based on bilinear forms,the solutions to dimensionally reduced generalized variable coefficient B-type Kadomtsev-Petviashvili equation in(3+1)-dimensions are computed through symbolic computation.The property of solutions is investigated and exhibited vividly by three dimensional plots and contour plots.

Keywords: rational solution;Bell polynomial theories;bilinear forms; fluid dynamics

1 Introduction

The study of nonlinear evolution equations which are regarded as the models to describe nonlinear phenomena became more attractive topic in physical science[1].Many methods were proposed over years to address the nonlinear evolution equations,such as inverse scattering transformation[2,3],Darboux transformation[4],Hirota method[5],Bcklund transformation[6],Bell polynomials[7].Through these methods,many kinds of solutions are presented.As a kind of solutions,the rational solution to some nonlinear partial differential equations are studied.The aim of this study is to use the Hirota bilinear equations to generate the generalized(3+1)dimensional variable coefficient B-type Kadomtsev-Petviashvili equation and then study the solutions to its two dimensionally reduced cases in(2+1)-dimensions.

The Kadomtsev-Petviashvili equation[8],

is a nonlinear partial differential equation.The rational solutions were exhibited by symbolic computation[9].Furthermore,the bilinear formulation plays a key role in the study of rational solutions,which is defined as[10]:

Extended from(1.1),a generalized(3+1)dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation[11],

wherea(t)andb(t)are the real function oftandρis a real non-zero constant.

In this study,we would like to present the bilinear form for(1.2)generated from a generalized bilinear differential equation.The solutions will be generated from polynomial solutions.In Section 2,the solutions to the first dimensionally reduced case,the second dimensionally reduced case,forz=xandz=y,are constructed.Finally,some conclusions are given in Section 3.

2 Bilinear Forms and Solutions

wherefas a function ofx,y,z,andt,the bilinear differential operators,are the Hirota bilinear operators.

Iffsolves generalized equation(2.1),thenpresent the solutions to(1.2).In this study,we construct positive quadratic function solution to the dimensionally reduced Hirota bilinear equation(2.1)for two cases:z=xandz=y,and begin with

whereai(1≤i≤9)are all real parameters to be determined.

2.1 With z=x

The dimensionally reduced Hirota bilinear equation(2.1)in(2+1)dimensions

which is transformed into

Through the link betweenfandu,substituting(2.2)into(2.3)to the following set of constraining equations for the parameters

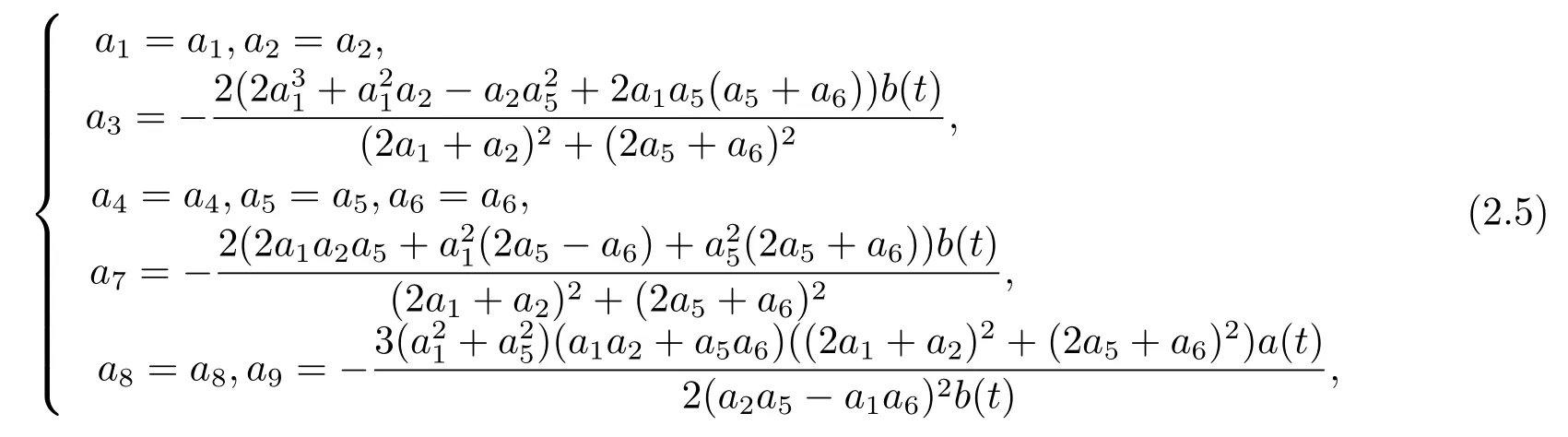
which satisfies the conditions

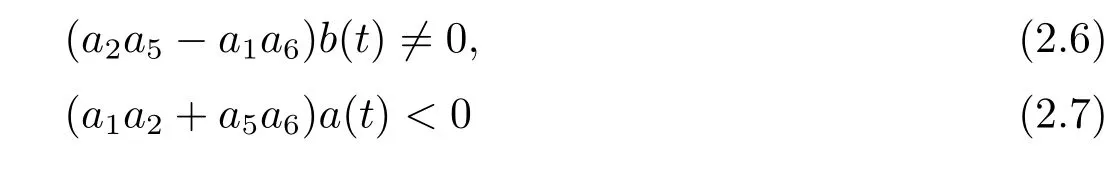
to guarantee the rational localization of the solutions.The parameters in set(2.5)yield a class of positive quadratic function solution to(2.2)as

through transformation as

and the functiong,hare given as follows

Figure 1:Profiles of(1.1)with t=−2,0,4:3d plots(left)and contour plots(right)

The solutionuinvolves six parametersa1,a2,a4,a5,a6anda8.All six involved parameters are arbitrary and the rest are demanded to satisfy conditions(2.6)and(2.7).We choose the following special set of parameters

2.2 With z=y

The dimensionally reduced Hirota bilinear equation(2.1)turn out to be

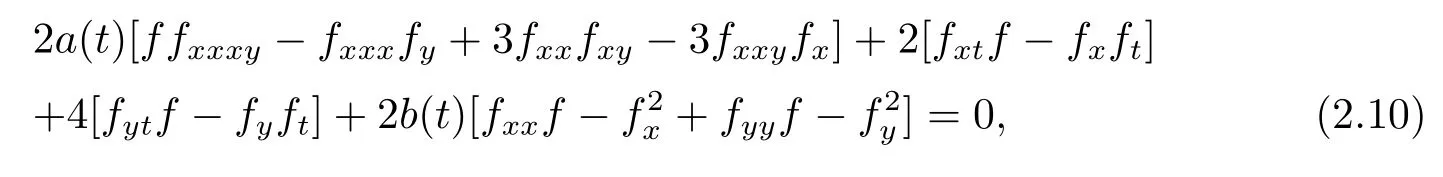
which is transformed into

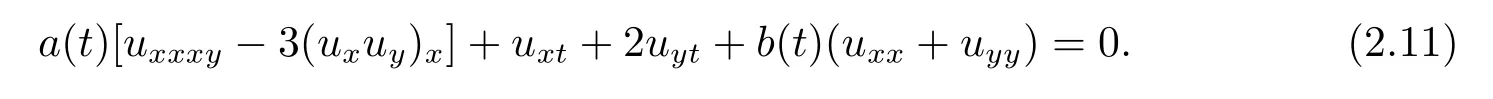
Through the link betweenfandu,substituting(2.2)into(2.10),the following set of constraining equations for the parameters

which needs to satisfy the conditions

to guarantee the analyticity and rational localization of the solutions.The parameters in set(2.12)yield a class of positive quadratic function solution to(2.10)as

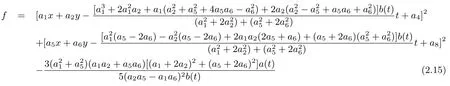
through transformation as

and the functionsg,hare given as follows

The solutionuinvolves six parametersa1,a2,a4,a5,a6anda8.All six involved parameters are arbitrary and the rest are demanded to satisfy(2.13)and(2.14).To get the special solutions of the equation,let us choose the following special set of the parameters

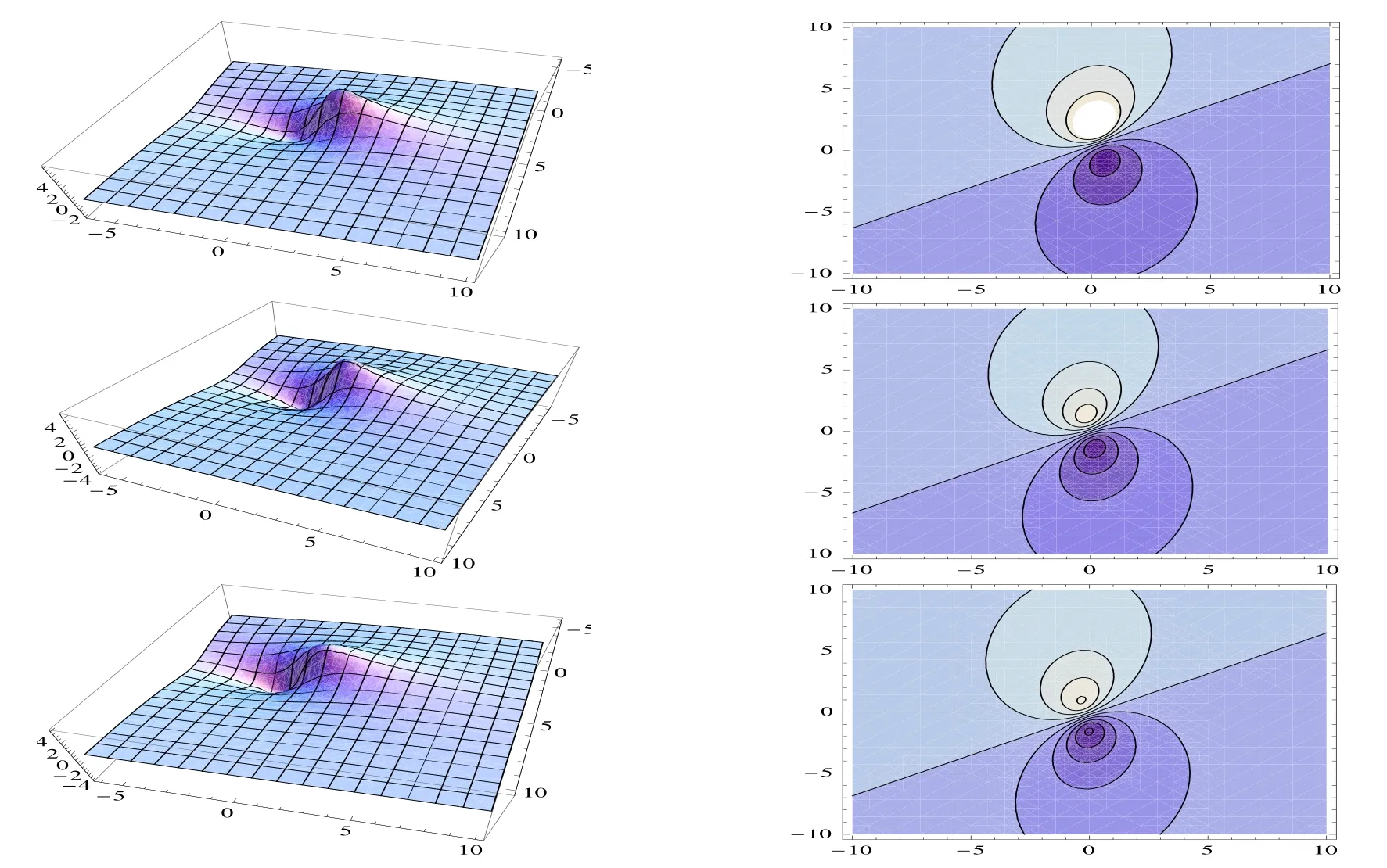
Figure 2:Profiles of(1.1)with t=−1,0,:3d plots(left)and contour plots(right)

3 Conclusion

In this paper,via the Bell polynomials and Hirota method,we have derived bilinear form for(1.2).Then by searching for positive quadratic function solutions to(2.3)and(2.10),two classes of solutions to the dimensionally reduced equations are presented.These results provide some salutary information on the relevant fields in nonlinear science.Therefore,we expect that the results presented in this work will also be useful to study lump solutions in a variety of other high-dimensional nonlinear equations.