等离子鞘套随机特性对电波传播影响分析

刘江凡，李 慧，焦子涵，白光辉，席晓莉

(1.西安理工大学自动化与信息工程学院，陕西西安7100482.中国运载火箭技术研究院 空间物理重点实验室，北京100076)

高超声速飞行器在大气层中飞行时，飞行器与其周围空气剧烈摩擦，使空气分子及飞行器表面材料发生电离，形成等离子鞘套。等离子鞘套的存在，使得投射其上的电磁波产生反射、折射及散射，而在其中传播的电磁波受到衰减，从而影响飞行器的导航、遥测和通信信号的传输，在某些条件下甚至会导致飞行器与卫星和地面的无线电联系完全中断，形成黑障效应。

早在20世纪60～90年代，已有学者对再入黑障问题开展了大量理论与试验研究，取得了许多重要进展[1-6]。总体来看，这些早期的研究主要从无线电频段选取、电波传播特性计算、鞘套对天线性能影响以及黑障的削弱技术等方面开展。

近些年来，针对等离子鞘套引起的通信中断问题的研究，除采用更为完善的电磁数值计算方法，分析计算稳态情况下等离子鞘套中电波传播特性[7]、鞘套的电磁散射特性[8-9]以及其对天线特性的影响[10-11]外，在研究鞘套中电波传播特性方面，研究者开始更多地关注再入湍流等离子的随机变化特性对电波传播的影响[12-18]。

本文将色散媒质的线性分段递归卷积(Piecewise Linear Recursive Convolution， PLRC)FDTD方法[19]与S-FDTD方法结合，提出了S-PLRC-FDTD方法，并采用该方法进一步分析了典型鞘套电子密度分布下，电子密度随机特性对电波信号影响。

1 等离子体的S-PLRC-FDTD算法

各向同性、碰撞的冷等离子体中，电磁波满足的Maxwell相关方程和本构方程如下：

(1)

(2)

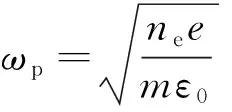
1.1 场量均值的迭代方程

采用FDTD方法计算时，需要将式(2)转换到时间域，并对其进行离散后得FDTD递推公式。本文采用色散媒质中常用的PLRC[19-20]方法，得到等离子体中电场的迭代方程。以电场x分量为例，其的迭代方程如下：

(3)

式中C1与C2是与等离子体参数相关的两个系数，可表示为：

(4)

其中g1=Δt/2υ+a1/υ3Δt,g2=Δt/υ-a2/υ2-g1,a1=-1+(1+υΔt)exp(-υΔt),a2=1-exp(-υΔt)。

φxn=k1ωp2Exn+k2ωp2Exn-1+

exp(-υΔt)φxn-1

(5)

其中:k1=-a2a1+a2υΔt/υ3Δt，k2=a1a2/

υ3Δt。

磁场的均值迭代方程与普通媒质一致，在此不再赘述。

1.2 场量方差的迭代方程

本小节将推导等离子体中电场及其辅助变量标准差的迭代公式。在推导过程中，仍遵循文献[16, 18]给出相关准则。

首先推导电场方差的迭代公式，将式(3)两端同乘(ε+ωp2g2)可以得到：

εEx|n+1+g2ωp2Ex|n+1-ε

(6)

对式(6)左右两端同时取方差：

σ2εEx|n+1+g2ωp2Ex|n+1-εEx|n+

g1ωp2Ex|n-φx|n=σ2Δt/ε0·

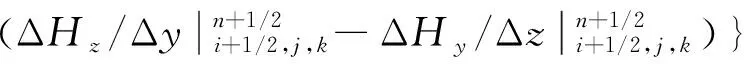
(7)

当相关系数取如下近似时：

(8)

式(7)可简化为：

(9)

对式(9)中左端σωp2Ex|n+1和σωp2Ex|n两项使用delta法[16, 18]进行展开，第一项可以写为：

(10)

σωp2Ex|n+1≈2ρωp,Ex|n+1ωpEx|n+1σωp+ωp2σEx|n+1

(11)

类似地，σωp2Ex|n项可以化简为：

σωp2Ex|n≈2ρωp,Ex|nωpEx|nσωp+ωp2σEx|n

(12)

将式(11)～(12)代入式(9)中可以得到σEx|n+1的迭代方程：

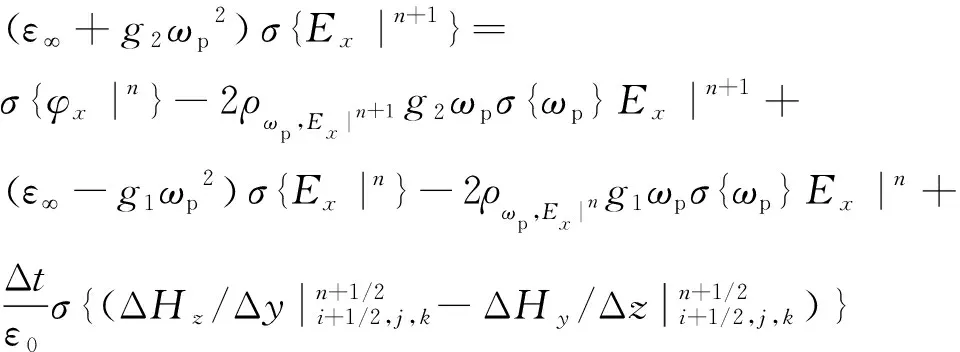
(13)

式(13)即为等离子体中的S-PLRC-FDTD场值方差迭代公式。

接下来我们将进一步推导辅助变量φx的方差迭代公式。对式(5)两端同时取方差得：

(14)

对式(14)中k1σ2ωp2Exn和k2σ2ωp2Exn-1两项使用delta法[18]，可得：

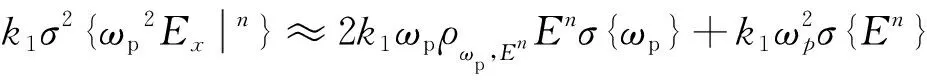
(15)

k2σ2ωp2Exn-1≈2k2ωpσωpExn-1+k2ωp2σExn-1

(16)

将式(15)～(16)代入式(14)中，可以得到等离子体中的S-PLRC-FDTD辅助变量标准差的迭代公式为：

(17)

需要指出的是，式(13)与式(17)中等离子体频率与电场相关系数ρωp,Ex仍需要进一步确定，其取值会直接影响S-PLRC-FDTD对场量标准差的估计。

2 计算模型与结果分析

鞘套电子密度分布常采用双指数或双高斯模型描述。在本文计算中，假设鞘套内稳态(平均)电子密度分布具有如下双高斯分布特性：

(18)

式中：ne,peak为电子密度峰值，zT为等离子体厚度，zB为峰值电子密度所处位置，a1,a2为描述电子密度衰减程度的参数。

由于电子密度分布受飞行高度，飞行速度，再入攻角，再入湍流等因素的影响，鞘套中电子密度并不恒定，电子密度具有一定的随机特性，其电子密度可用如下模型描述：

ne(z)=ne_steadyz1+Δδne

(19)

式中：Δ表示电子密度相对变化幅度，δne为一标准正态分布随机变量，因此电子密度标准差σne可以表示为σne=Δ·ne_steady，相应的等离子体角频率方差可以表示为σωp=0.5Δωp_steady。

选取鞘套参数如下：a1=1 cm-2，a2=0.5 cm-2，zT=15cm,zB=5cm，峰值电子密度均值ne,peak=1×1017m-3，碰撞频率υ=1×109rad/s。采用S-PLRC-FDTD方法，分别计算了电子密度相对变化幅度Δ=5%，Δ=10%，Δ=20%时，其对电波传播的影响。S-PLRC-FDTD采用1 mm均匀网格剖分，时间步长Δt=Δz/2c。计算模型见图 1，等离子体占据50～199网格(15 cm)。所加源为电场x方向极化的正弦平面波，其振幅为1 V/m，位于z方向第40网格处，观测点位于第210网格处。

图1 计算模型Fig.1 Simulation model

图2给出了入射波频率为1 575 MHz和4 000 MHz正弦波时，不同电子密度变化下，S-PLRC-FDTD方法计算得到的观测点电场平均值。由于等离子鞘套的存在，透射电磁波存在衰减，透射波电场振幅分别衰减到0.544 V/m(衰减5.3dB)和0.941 V/m(衰减0.45 dB)。入射波频率越高，衰减越小。

图2 平面波入射时观测点电场均值比较Fig.2 Comparison of mean electric field values in plane wave incident

为了验证S-PLRC-FDTD方法的正确性，将Monte Carlo结合传统PLRC-FDTD计算结果也绘于图2中(Monte Carlo方法共采用1000组样本)。可以发现S-PLRC-FDTD方法与Monte Carlo方法计算的电场平均值几乎重合。

图3分别给出1 575 MHz平面波入射下，电子密度相对变化幅度分别为Δ=5%，Δ=10%，Δ=20%时，观测点电场在不同时刻的电场的方差值。与预期结果一致，当电子密度变化(标准差)越大，电场的方差也就越大。

在S-PLRC-FDTD方法中，Ex与ωp互相关系数ρEx,ωp的选取，会直接影响到电场方差的计算结果。ρEx,ωp=1时S-PLRC-FDTD会过高地估计电场的方差，相应的，当ρEx,ωp=0.8时，估计值偏低。在本例中，当ρEx,ωp=0.95时，S-PLRC-FDTD与Monte Carlo结果吻合最好。

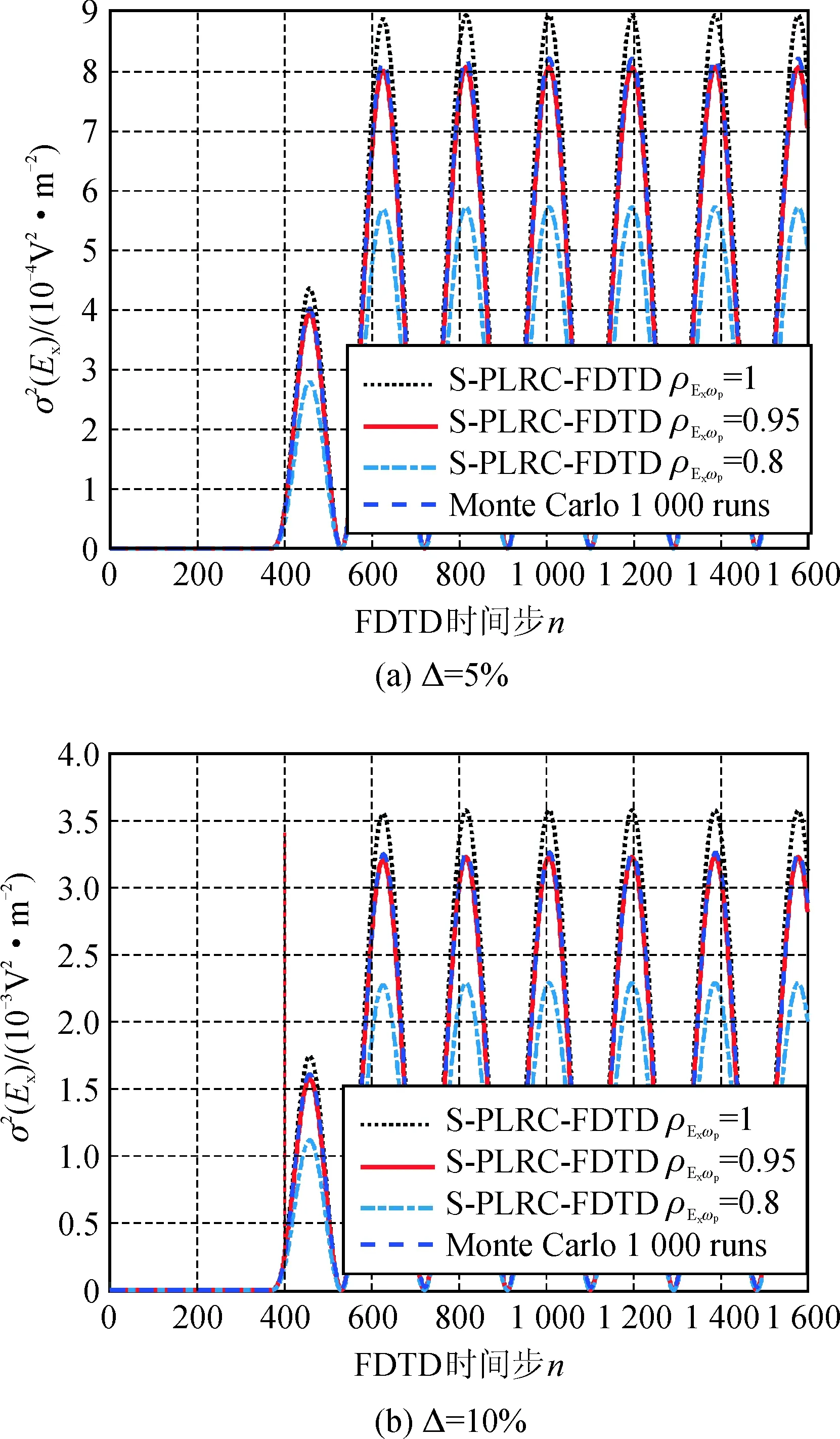
图3 1 575 MHz平面波入射时观测点方差比较电子密度相对变化幅度Fig.3 Comparison of observation point variances in 1 575 MHz plane wave incident

笔者也对4 000 MHz平面波入射情况进行了计算，同样当ρEx,ωp=0.95时，S-PLRC-FDTD结果与Monte Carlo结果吻合最好。

由于S-PLRC-FDTD在每次迭代过程中，需要额外计算各场量的标准差，因此S-PLRC-FDTD内存占用及每步计算用时约为传统PLRC-FDTD的2倍。但相比于传统PLRC-FDTD需要通过1 000次甚至更多的Monte Carlo仿真获得统计特性，S-PLRC-FDTD具有显著优势。

为进一步评估电子密度随机变化对电磁波相位和幅度的影响，采用S-PLRC-FDTD方法，计算了上述鞘套在不同入射波频率以及不同碰撞频率情况下，透射系数幅度与相位的变化情况。

图4给出了电子密度相对变化幅度Δ=10%时，透射系数幅度1σ误差棒图。从图4中可以发现，当入射波频率较低ω/ωp≪1时，透射系数随着碰撞频率的增加而增加，当入射波频率较高时，透射系数随着碰撞频率的增加而减少。

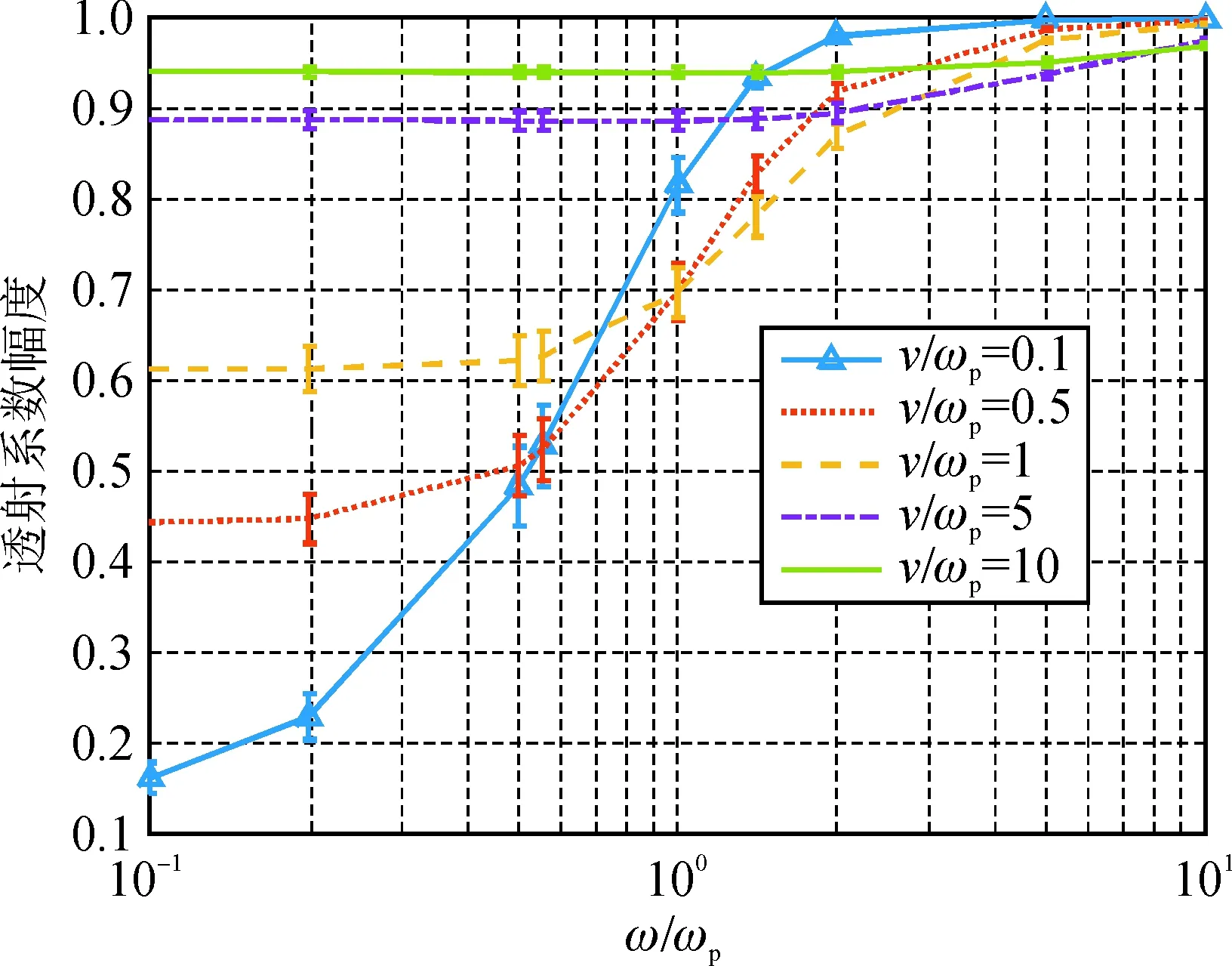
图4 电子密度相对变化幅度Δ=10%时不同碰撞频率下透射系数幅度的1σ误差棒图Fig.4 1σ error bar graph of transmission coefficientamplitude at different υ/ωp in the relative intensity of electron density variability Δ=10%

图5给出了电子密度相对变化幅度分别为Δ=5%，Δ=10%，Δ=20%时，不同碰撞频率下，透射系数幅度的标准差随入射波频率的变化。

从图5可以发现，透射系数幅度标准差正比于电子密度相对变化幅度变化。从图5中还可以发现，等离子碰撞频率越高时，透射系数标准差随入射波频率变化越缓慢，当υ/ωp>1时，低频段透射系数标准差基本不变；对高频入射波ω/ωp>1，透射系数标准差随着入射波频率的增加而减小，并且碰撞频率越小，透射系数标准差减小越快。总体而言，提高入射波频率有利于减低电子密度变化对透射系数幅度的影响。

图6给出了电子密度相对变化幅度分别为Δ=5%，Δ=10%，Δ=20%时，透射系数相位标准差随入射波频率的变化。

从图6中可以发现，透射系数相位标准差同样正比于电子密度相对变化幅度。在电子密度变化幅度相同时，碰撞频率越高，透射系数相位标准差越小，随入射波频率的变化也越缓慢，并且对于低碰撞频率υ/ωp≤1的等离子体，透射系数相位标准差最大值出现在ω/ωp≈1附近，随着碰撞频率的提高，透射系数相位标准差最大值逐渐向高频方向移动。

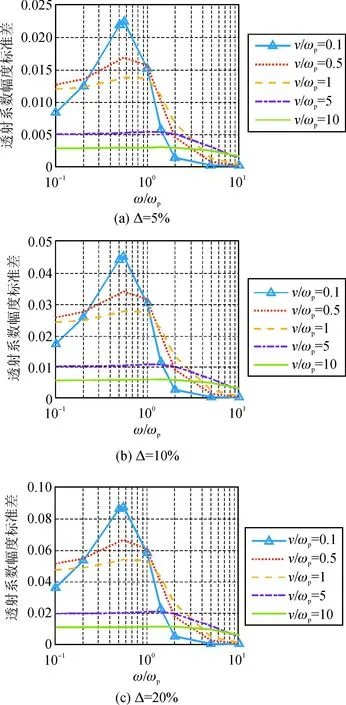
图5 不同碰撞频率下透射系数标准差比较Fig.5 Comparison of standard deviations of transmission coefficient amplitude at different υ/ωp

表1和表2进一步给出了电子密度相对变化幅度Δ=10%时，S-PLRC-FDTD方法与Monte Carlo结合SMM方法(1 000次样本)计算结果比较。

从表1～2中可以发现，S-PLRC-FDTD方法的计算结果与Monte Carlo结合SMM方法的计算结果具有很好的一致性。与Monte Carlo结合SMM方法相比，S-PLRC-FDTD方法的优势在于它可以通过一次计算，获得观测点波形在所有时刻的均值与方差。

此外，对于更为复杂的鞘套模型(二维或三维情况)，S-PLRC-FDTD方法也具有适用性。

图6 不同碰撞频率下透射系数相位标准差比较Fig.6 Comparison of standard deviations of transmission coefficient phase at different υ/ωp

υ/ωpMonte Carlo + SMM方法下的标准差/(°)S-PLRC-FDTD方法下的标准差/(°)ω/ωp=0.2ω/ωp=0.5ω/ωp=1ω/ωp=2ω/ωp=0.2ω/ωp=0.5ω/ωp=1ω/ωp=20.10.877 03.165 04.004 92.037 50.848 33.142 93.913 32.064 80.50.088 41.048 42.426 61.873 10.072 50.958 22.436 21.846 510.048 70.380 51.263 71.523 50.035 80.388 41.238 71.515 550.006 00.023 30.084 00.228 90.004 50.024 00.081 90.224 2100.001 80.006 40.021 80.062 80.001 40.006 50.020 90.056 4

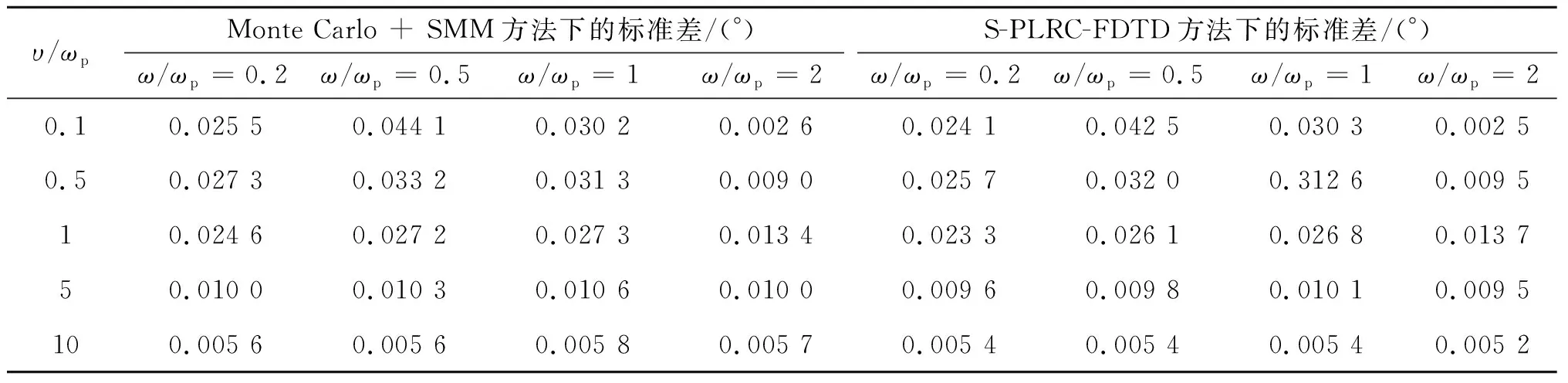
表2 透射系数幅度标准差

3 结 语

本文采用S-PLRC-FDTD方法，计算了电子密度为高斯分布的等离子鞘套中电子密度随机变化对入射信号的影响，分析了电子密度抖动引入的相位抖动和振幅抖动。结果表明：电子密度的随机变化与其引起透射电磁波的幅度与相位的抖动具有显著的正相关性；在相同电子密度变化条件下，υ/ωp越大，透射系数幅度与相位的标准差随频率的变化越小；对于低碰撞频率υ/ωp≤1的等离子体，透射系数相位标准差最大值出现在ω/ωp≈1附近，随着碰撞频率的提高，透射系数相位标准差最大值逐渐向高频方向移动；总体而言，提高入射波频率，有助于有减少透射电磁波幅度与相位抖动。