重力姿轨耦合效应引起的太阳能电站轨道共振

刘玉亮，邬树楠，张开明，吴志刚

1. 大连理工大学 航空航天学院，大连 116024 2. 大连理工大学 工业装备结构分析国家重点实验室，大连 116024

空间太阳能电站(Space Solar Power Station, SSPS)的概念是由美国科学家Peter Glaser博士于1968年提出[1]。其工作原理可概述为：通过放置在地球轨道上的超大型太阳能电池阵列收集太阳能，并将其转换成微波传输到地面，之后再将微波转换成电能供用户使用。相比于地面太阳能发电系统，SSPS具有发电效率高，不受昼夜和天气的影响等优点[2]。

与传统卫星相比，SSPS具有超大型的结构，其结构尺寸常达至千米甚至几十千米的量级[2-6]，这个特点使得重力姿轨耦合效应对其轨道运动和姿态运动带来的影响将不能再忽略不计。实际上，卫星在轨运行过程中的轨道运动和姿态运动是通过重力梯度弱耦合在一起的；这种耦合效应的大小与卫星的质量分布，特征尺寸及其指向有关[7]。传统卫星因具有较小的结构尺寸，在关于其轨道运动和姿态运动的研究中常忽略它们之间的重力姿轨耦合效应。这种做法也应用在一些关于SSPS轨道运动和姿态运动的研究中[8-13]。但对于SSPS这种具有超大型结构的卫星而言，应当重新分析重力姿轨耦合效应带来的影响。

目前，在关于SSPS在轨运行中重力姿轨耦合效应的研究中，国内外的学者已取得了一些初步的成果。基于Hamilton体系，邓子辰[14]，文奋强[15]，魏乙[16]等建立起了不同构型SSPS在轨运行过程中的重力姿-轨-结构振动耦合动力学方程，并通过数值仿真结果分析了其在轨动力学特性，但上述工作并没有研究重力姿-轨-结构振动耦合效应对其轨道，姿态，及其结构振动带来的影响。通过对耦合动力学方程进行线性化处理，Ishimura和Higuchi[17]研究了一种绳系SSPS在轨运行过程中轨道，姿态和结构振动之间的重力耦合动力学特性；研究结果表明该耦合作用对其轨道运动影响较小，可忽略不计。此外，通过借鉴天体力学领域中的一些方法和成果[18-19]，一些学者采用了相似的方法对SSPS在轨运行过程中的重力姿-轨-结构耦合动力学特性进行了分析[20-22]。其研究思路可大致概括为：首先将SSPS的结构简化成板或者梁的形式；之后将其受到的重力，重力梯度力矩和结构振动受到的广义重力进行级数展开，保留至有限项，进而得到一组具有较高计算精度但同时具有强非线性特性的动力学方程；最后通过数值仿真结果来评估重力姿轨耦合效应对其姿态运动，轨道运动和结构振动带来的影响。

然而，上述关于SSPS重力姿轨耦合效应的研究中，大都是仅仅通过数值仿真的方法进行研究[7,14-16,18-22]，并没有从动力学方程上揭示其内部的耦合机理。此外，由于上述研究中所建立动力学方程强非线性的特点，其所获得的仿真结果也往往具有随机性。其主要原因为：对于强非线性方程，其数值仿真结果常常与方程中变量的初值有关，而在上述研究中变量初值的选取是随意的。因此，为了更好地了解SSPS在轨运行过程中重力姿轨耦合效应带来的影响，有必要从解析的角度对其耦合动力学方程进行分析。先前一些学者的工作为可我们的研究提供参考[23-25]。

本文将重点研究任意相控阵天线式[6]SSPS在地球引力场中的重力姿轨耦合问题，并采用解析法与数值仿真相结合的方法对其耦合动力学特性进行研究。本文大致脉络如下：首先，通过Hamilton原理推导出SSPS的重力姿轨耦合动力学方程；之后，通过解析法对动力学方程进行分析；最后，进行数值仿真与分析，并给出本文的结论。

1 太阳能电站动力学方程建立

1.1 坐标系与假设

为了便于描述SSPS在空间中的运动，本小节将给出一些坐标系和符号的定义。这里忽略结构柔性振动带来的影响，将任意相控阵天线式SSPS简化为刚体，且只考虑轨道平面内的运动，如图1所示。Oe和O分别为地球质心和SSPS的质心。OeXeYe和OXoYo分别为惯性坐标系和轨道坐标系。OXbYbZb为SSPS的固联坐标系，其中，OXb、OYb和OZb均为惯性主轴，且共同构成右手坐标系。R为O相对于Oe的位置矢量。ρ为SSPS上任一质量微元dm相对于其质心O的位置矢量。r为dm相对于Oe的位置矢量，且满足：r=R+ρ。φ为OXb轴相对于OXo轴的转角，同时也是SSPS姿态运动的俯仰角。θ为位置矢量R相对于OeXe轴的转角。

图1 SSPS姿态运动和轨道运动示意图Fig.1 Schematic of orbital and attitude motions of SSPS

1.2 动力学方程

在本节中，将通过Hamilton原理推导出SSPS在地球引力场中的重力姿轨耦合动力学方程。

SSPS在轨运行过程中所具有的动能可表示为

(1)

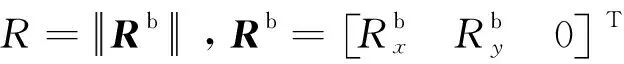
在地球引力场中，质量微元dm所具有的引力势能可表示为

(2a)

(2b)

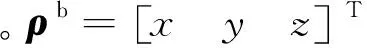
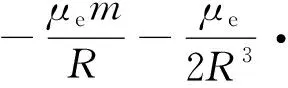
[(1-3sin2φ)Ixx+(1-3cos2φ)Iyy+Izz]

(3)

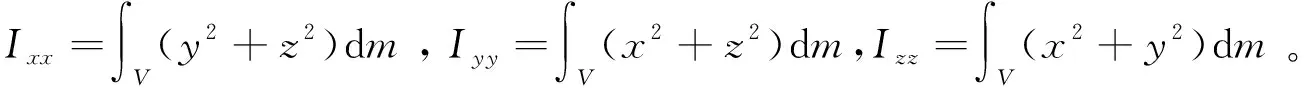
将式(1)和式(3)代入到Hamilton原理中：

(4)

可得到SSPS在地球引力场中运动时的重力姿轨耦合动力学方程为

(5a)

(5b)

(5c)

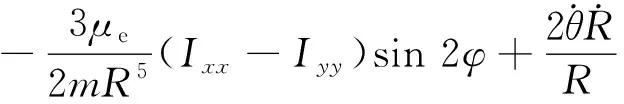
2 动力学特性分析

在本节中，将采用解析法对式(5a),式(5b)和式(5c)进行处理，进而分析SSPS在轨运行过程中的重力姿轨耦合动力学特性。

R=R0+ΔR

(6a)

(6b)

式中：ΔR和Δn分别为重力姿轨耦合效应作用下，SSPS的轨道半径和轨道角速度相比于圆形轨道的偏差。

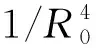
(7a)

(7b)

C1=R0Δn(t0)+2n0ΔR(t0)

(7c)

(7d)

式中：t0为起始时间，在本文中设t0=0。将式(7b) 和式(7d)中的sin 2φ和cos 2φ两项进行Fourier级数展开：

(8a)

(8b)

将式(8a)和式(8b)代入式(7b)和式(7d)，可得ΔR和Δn的解析解形式如下所示：当Tφ≠2iπ/n0(i=1,2,3,…)时，其解析解为

(9a)

(9b)

(9c)

(9d)

当Tφ=2kπ/n0(k=1,2,3,…)时，其解析解为

(10a)

(10b)

式中:ΔRp1、Δnp1、ΔRp2和Δnp2均表示方程中的周期变化的项；C2、C3为常数。

从式(9a)、式(9b)、式(10a)和式(10b)中还可以看出，当C2≠0和C3≠0时，ΔR和Δn中将存在常数项，这就意味着SSPS的实际轨道半径和实际轨道角速度将会产生相对于圆形轨道半径R0和轨道角速度n0的恒定偏差；由于Δn中存在常数项，SSPS的位置将会产生相对于圆形轨道的线性漂移，即Δθ将会随着时间线性增加(或减小)。当C3=0时，即满足条件：

(11)

SSPS的位置漂移将会消失。从式(11)中可以看出，当SSPS的姿态运动规律确定时，通过选择适当的C1，即Δn(t0)和ΔR(t0)的值，即可消除重力姿轨耦合效应引起的位置漂移。设SSPS的姿态运动为角速度为n0的恒定转动，φ的初始值为φ0=0 rad，将上述参数代入式(11)，并设Δn(t0)=0 rad/s(或ΔR(t0)=0 km)，可得

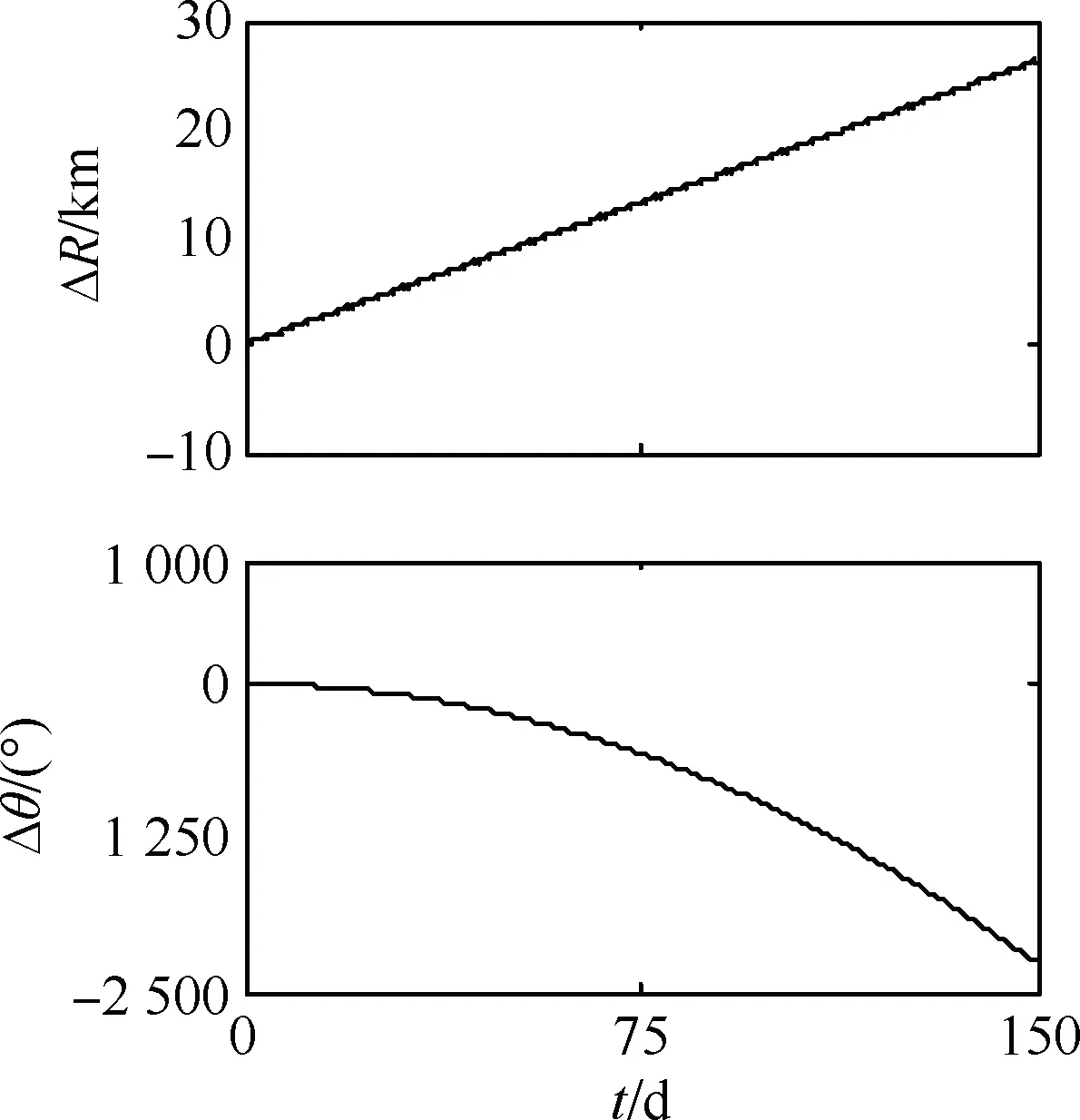
图2 存在恒定对地指向误差时线性模型SSPS的轨道动力学行为Fig.2 Orbital dynamic behaviors of SSPS computed by the linear model when there exists a constant earth-pointing error in the pitch angle

(12a)

(12b)

不同轨道初始条件下，ΔR和Δθ随时间的变化规律如图3所示。其中，情况1所对应轨道运动初值为：ΔR(t0)=(2Izz-2.5Ixx+0.5Iyy)/(4mR0)，Δn(t0)=0 rad/s；情况2所对应轨道运动初值为：ΔR(t0)=0 km，Δn(t0)=0 rad/s。从图3中可以看出，当SSPS的姿态运动规律已知时，通过合理地选择轨道运动的初始条件即可消除重力姿轨耦合效应引起的位置漂移。

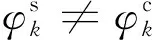
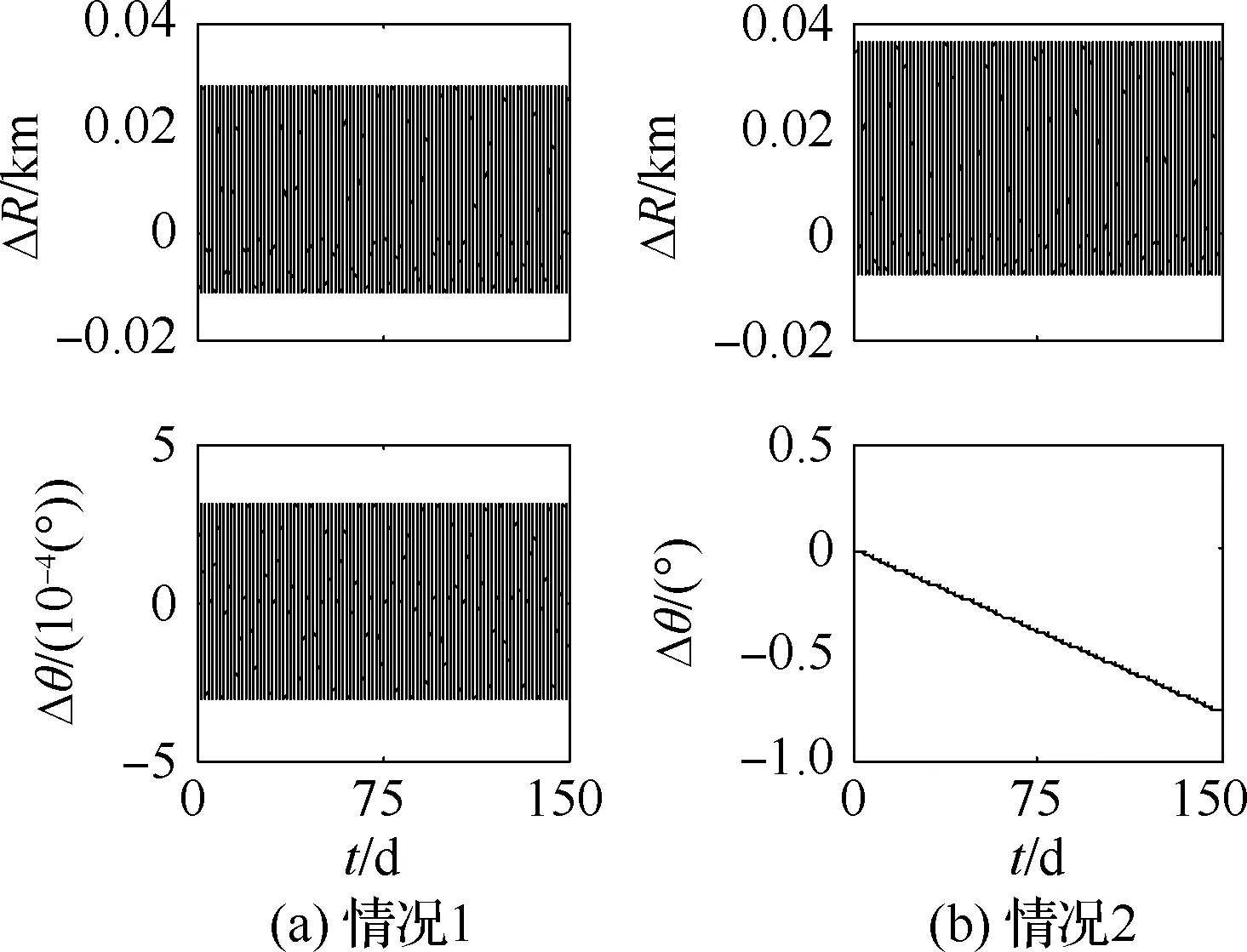
图3 不同轨道初始条件下线性模型 SSPS的轨道动力学行为Fig.3 Orbital dynamic behaviors of SSPS computed by linear model corresponding to different initial conditions of orbital motion

图4 共振发生时线性模型SSPS的轨道动力学行为Fig.4 Orbital dynamic behaviors of SSPS computed by linear model when resonance in orbital motion occurs

3 重力梯度稳定式空间太阳能电站

为了节约运行成本，SSPS的主体结构常被设计成重力梯度稳定式的[3-4,6]。接下来将讨论无外界作用力下，重力梯度稳定式SSPS的姿态和轨道动力学特性。相比于SSPS受到的重力梯度力矩，重力姿轨耦合效应对其姿态运动产生的干扰为小量[20-22]。设外界作用力矩τ=0，且先忽略重力姿轨耦合效应带来的影响，其姿态运动方程为

(13)

式中：kz=(Ixx-Iyy)/Izz。

在本文中仅考虑姿态运动为摆动的情况，设φ0=0 rad，则式(13)的解为[26]

(14a)

(14b)

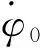
(15)

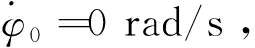
将式(14a)代入sin 2φ和cos 2φ，并进行Fourier级数展开可得

(16a)

(16b)

式中：k=1,2,3…；从式(16a)和式(16b)可以看出，由于Jocobian椭圆函数特殊的性质[23]，sin 2φ的Fourier级数中仅含有奇次项谐波分量，而cos 2φ的Fourier级数中则仅含有偶次项谐波分量。由第2节的分析可知，由于A0=0，故在此种运动模式下，ΔR和Δn中将不存在随时间线性增长的项。此外，当Ixx≠Iyy，且满足条件：Ts=2kπ/n0(k=1,2,3，…)，Ak≠0或Bk≠0时，SSPS的轨道运动将会产生共振。将式(16)与式(15) 进行联合可得

(17)

图5 不同初始姿态角下K(d)的值Fig.5 Values of K(d)corresponding to different values of initial pitch angles

从式(17)可以看出，当SSPS的初始姿态条件d和其质量分布特性参数kz满足一定条件时，其轨道运动将会产生共振。然而，当k取值较大时，共振常不易发生；其主要原因有3个：① 当k取值较大时，式(16a)和式(16b)所对应的共振分量的幅值很小，几乎为零；② 对于固定kz，越大的共振周期对应的初始姿态角φ0越大；由图5可知，φ0越大，其摆动周期对φ0的变化越敏感，这就意味着由微小的外界扰动(如上述分析中所忽略的重力姿轨耦合效应带来的扰动)引起的φ0微小变化将会引起摆动周期很大的变化，进而会抑制共振的产生；③ 对于很小的kz，其所对应的重力梯度力矩也会很小(如式(13)所示)。此时，重力姿轨耦合效应产生的干扰力矩将会对其姿态运动产生较大影响，从而会抑制共振的产生。

从图6中可以看出，当SSPS的初始姿态角较小时，其共振情况所对应的kz约为kz=1/3，kz=1/12 及kz=1/27。其原因为：当d取值较小时，即SSPS的姿态运动为小角度的摆动时，K(d)≈0.5π，将其代入式(17)可得小角度摆动时轨道运动共振所对应的kz为

(18)

由于重力梯度稳定的卫星常常在平衡位置附近做小角度的摆动，因此在对SSPS的质量分布特性参数kz进行设计的过程中，应当尽量避开式(18) 中所对应的kz的值。

图6 共振条件下不同kz对应的初始姿态角φ0Fig.6 Values of initial φ0 corresponding to different values of kz under the resonance condition

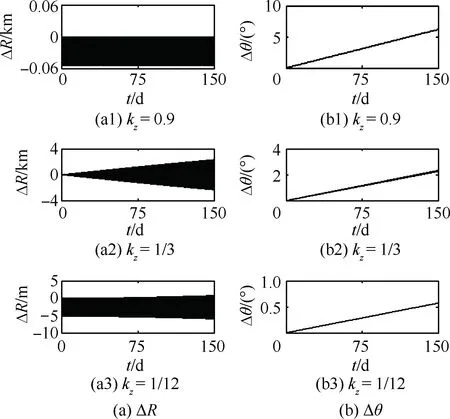
图7 不同kz下线性模型SSPS的轨道动力学行为Fig.7 Orbital dynamic behaviors of SSPS computed by linear model corresponding to different values of kz

4 数值仿真与分析

为了验证第2节和第3节中分析的正确性，本节将采用未简化后的方程组(式(5a)，式(5b)和式(5c))进行仿真，并与第2节和第3节的仿真结果进行对比。当SSPS存在恒定的对地指向误差时的轨道动力学特性如图8所示，其中，仿真初值与图2相同。

从图8中可以看出，ΔR和Δn的变化规律与变化范围均与图2相同，说明了第2节中理论分析的正确性。

不同轨道初始条件下，SSPS的轨道动力学特性如图9所示，其中，仿真条件和初值与图3相同。从图9中可以看出，两种情况下，ΔR和Δn的变化规律与变化范围与图3大致相同，但略有区别，其微小的差别是由忽略的高阶非线性项导致的。

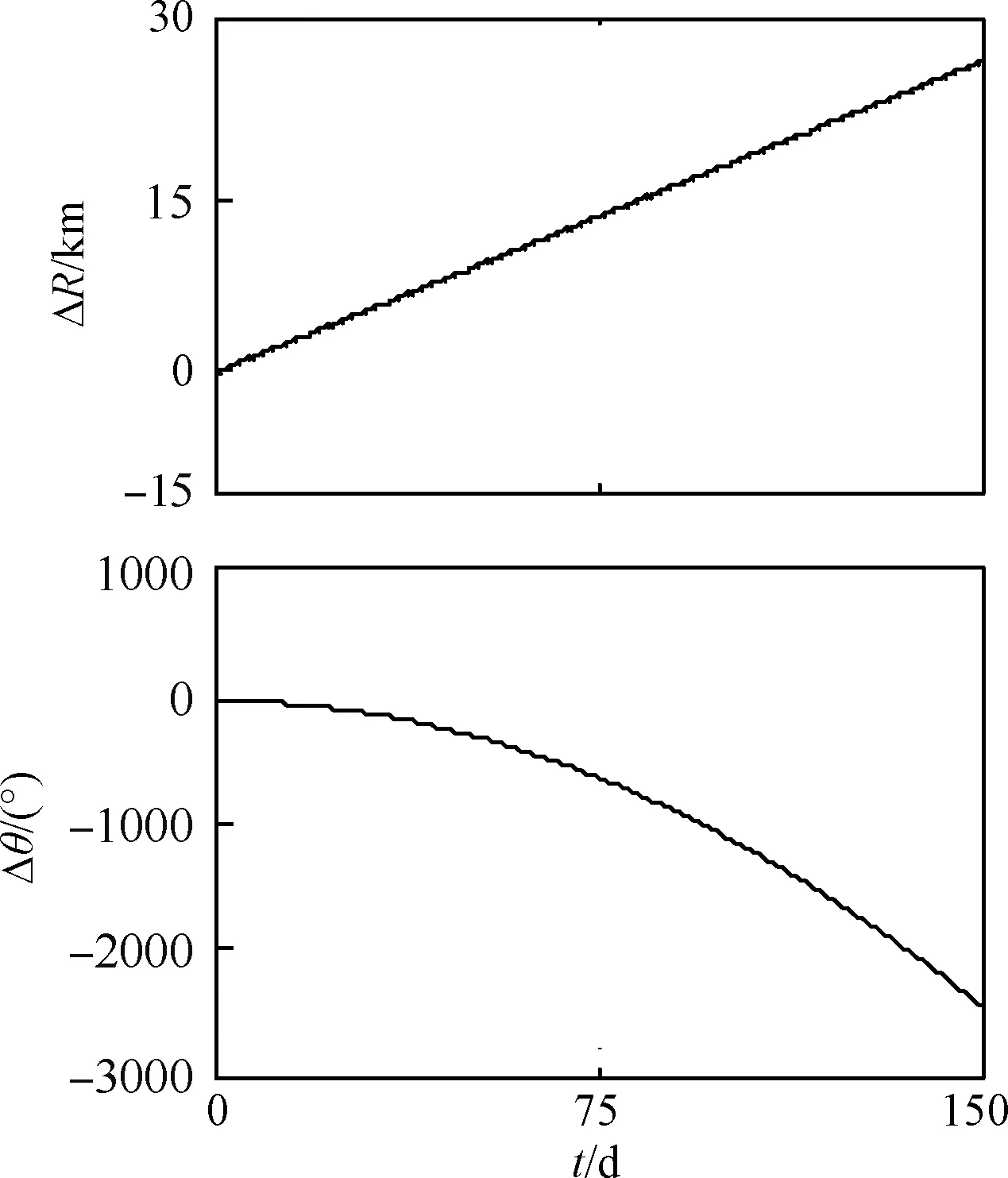
图8 存在恒定对地指向误差时非线性 模型SSPS的轨道动力学行为Fig.8 Orbital dynamic behaviors of SSPS computed by the nonlinear model when there exists a constant earth-pointing error in the pitch angle

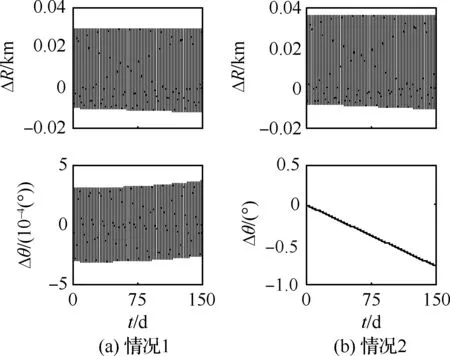
图9 不同轨道初始条件下非线性模型 SSPS的轨道动力学行为Fig.9 Orbital dynamic behaviors of SSPS computed by nonlinear model corresponding to different initial conditions of orbital motion

当SSPS的姿态角φ以0.5n0的恒定姿态角速度旋转时(即满足共振条件时)的轨道动力学特性如图10所示。其中，仿真的初始条件与图4相同。从图10中可以看出，ΔR和Δn的变化规律和变化范围与图4差别较大，其主要原因是随着ΔR的增加，图4中所忽略的高阶非线性项将会改变式(7a)的共振频率，进而会抑制共振的发生。相似的分析已在第2节中进行了说明。

当仅考虑SSPS受到的保守力，且其质量分布特性参数kz取不同的值时，其轨道动力学特性如图11所示，其姿态动力学特性如图12所示。其中，仿真的初始条件与图7相同。

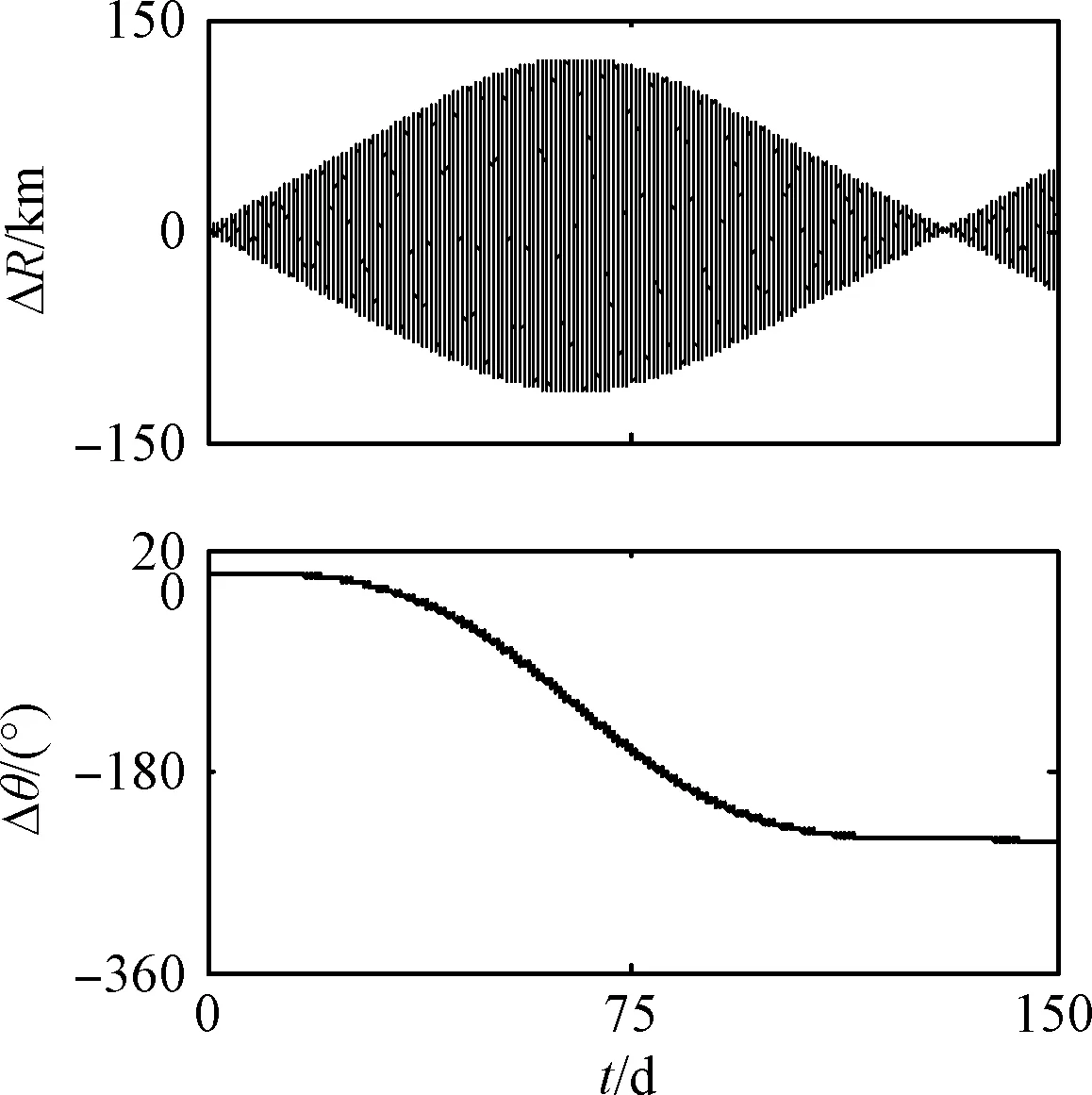
图10 共振发生时非线性模型SSPS的轨道动力学行为Fig.10 Orbital dynamic behaviors of SSPS computed by nonlinear model when resonance in orbital motion occurs

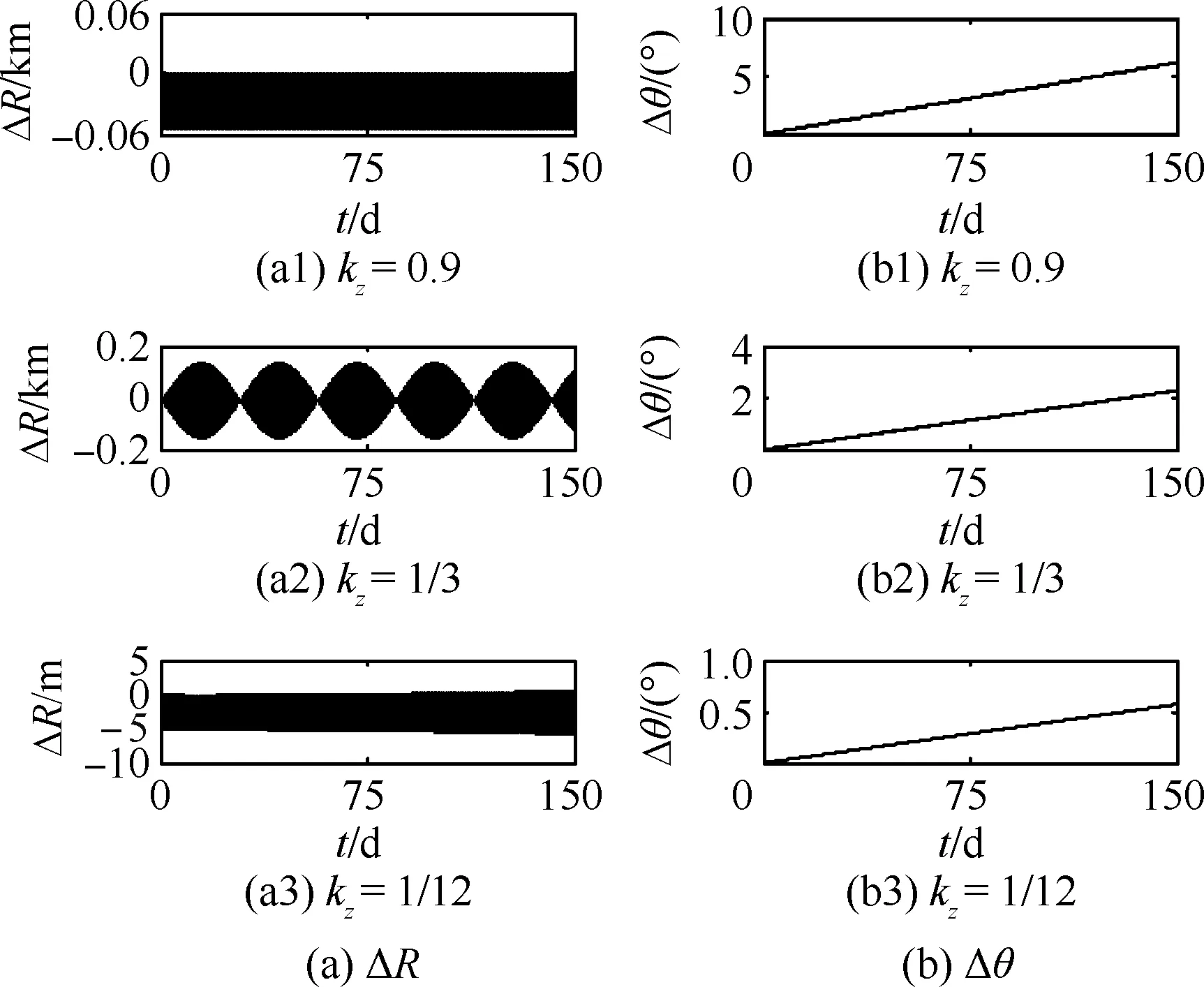
图11 不同kz下非线性模型SSPS的轨道动力学行为Fig.11 Orbital dynamic behaviors of SSPS computed by nonlinear model corresponding to different values of kz

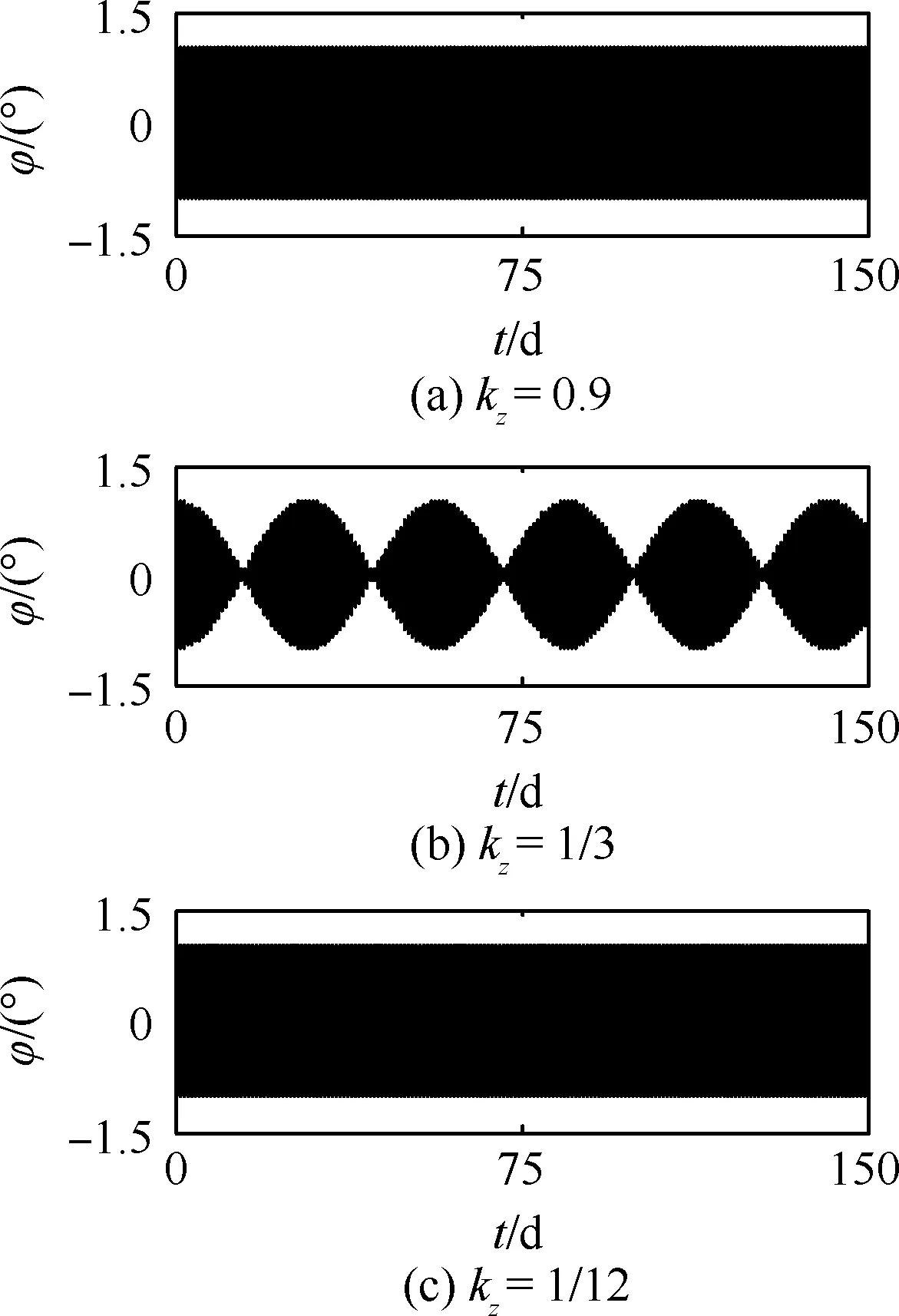
图12 不同kz下非线性模型SSPS的姿态动力学行为Fig.12 Attitude dynamic behaviors of SSPS computed by nonlinear model corresponding to different values of kz

从图11和图12可以看出，当kz=0.9和kz= 1/12时，ΔR和Δn的变化规律和变化范围与图7相同；其姿态运动也均为等幅振动，说明了第3节中分析的正确性。其中，当kz=1/12时未发生共振的原因为：式(16a)和式(16b)中的共振分量幅值很小，几乎为零，且此时SSPS受到的重力梯度力矩较小，其姿态运动周期易受到重力姿轨耦合效应的影响，进而抑制了共振的产生。此外，从图11和图12中还可以看出，当kz=1/3时，ΔR和Δn的变化规律和变化范围与图7差别较大，其主要原因为：随着ΔR的增加，其姿态运动的周期将会受到轨道运动的影响而产生变化(如式(5c)所示)，进而会抑制共振的发生。而且从图12中还可以看出，当kz=1/3时，姿态运动的振动幅值产生了周期性的变化，其主要原因是由于当仅存在保守力时，重力姿轨耦合效应会引起轨道运动和姿态运动之间的周期性能量交换。在起始时刻，SSPS姿态运动摆动周期为共振周期，轨道运动产生共振，能量从姿态运动向轨道运动进行转移，由于总能量恒定，故姿态运动能量变小，即振幅减小；随着ΔR振幅的增加，重力姿轨耦合效应产生的干扰力矩会改变姿态运动摆动周期，进而轨道运动共振会受到抑制，能量又从轨道运动向姿态运动进行转移，如此循环往复。类似的现象也存在于Mohan等[25]的分析中。

5 结 论

通过采用解析的方法研究了任意相控阵天线式空间太阳能电站在轨运行过程中重力姿轨耦合作用对其姿态运动和轨道运动的影响，并进行了数值仿真，研究结果表明：

1) 当空间太阳能电站的姿态运动满足一定规律时，轨道运动将会产生共振。

2) 重力姿轨耦合效应会引起轨道运动的长期漂移，通过选择合适的轨道运动初始条件可以消除漂移；而且，当空间太阳能电站存在恒定的对地指向误差时，重力姿轨耦合效应还会引起轨道运动的发散。

3) 当空间太阳能电站只受到保守力作用，且kz=(Ixx-Iyy)/Izz=1/3时，其中，Izz为俯仰轴转动惯量，Ixx和Iyy为另外两轴转动惯量；小角度摆动下，重力姿轨耦合效应将会引起轨道运动产生共振，且姿态运动的振幅也将产生周期性变化，轨道运动和姿态运动之间存在周期性的能量交换。