考虑液质润滑的多自由度永磁球面电机设计与分析

李争 陈晴 郭鹏 王群京

摘要：为优化多自由度永磁球面电机结构设计，在考虑液质润滑球面轴承理论的基础上，确定合适参数以改善电机工作情况。对其基本结构建模并进行工作原理分析，基于混合驱动模式，实现电机多自由度运动;建立了适用于永磁球面电机润滑分析的数学物理模型，推导出Reynolds方程和油膜厚度方程，运用有限差分法和编程对方程进行数值求解。分析了偏心率，定转子间隙，电机转速，速度系数以及油膜粘度等参数对电机润滑性能的影响;并构建了实验样机和润滑油粘温实验平台，获取了粘度和测试温度与运转时间的关系。结果表明：在球坐标下所建立的润滑理论适用于多自由度永磁球面电机;在油膜厚度没有达到最小临界值时，偏心率，转速，速度系数和油膜粘度的增大以及定转子间隙的减小，能够有效提高油膜压力和承载能力。

关键词：永磁电机;球面轴承;多自由度;雷诺方程;润滑理论

中图分类号：TM301       文献标志码：A         文章编号：1007-449X

Abstract：  In order to optimize the structural design of multi-degree-of-freedom permanent magnet spherical motor， the appropriate parameters are determined to improve the operation conditions of the motor considering the fluid lubrication theory. The basic structure was modeled and its principle of work was analyzed. Based on the hybrid drive mode， the multi-degree-of-freedom movement is achieved. The mathematical physical model for the lubrication analysis of permanent magnet spherical motor was established， and the Reynolds equation and the oil film thickness equation were derived. The finite difference method and programming were applied to solve the equation numerically. The influence of eccentricity， the clearance between the stator and rotor， rotation speed， velocity coefficient and oil film viscosity on the lubrication performance of motor is analyzed. And the experimental platform for the prototype motor and oil film viscosity-temperature test was also built with the relationship between viscosity and test temperature and operation time derived. The results show that the lubrication theory established under the spherical coordinates is suitable for the spherical multi-degree-of-freedom motors. In the case of the thickness of oil film not up to the minimum critical value. When the eccentricity， rotational speed， velocity coefficient and oil film viscosity are increased and the clearance between stator and rotor is reduced， the oil film pressure and load-carrying capacity can be improved.

Key words： Permanent magnet motor; spherical bearing; multi-degree-of-freedom; Reynolds equation; lubrication theory

中图分类号：TM301     文献标志码：A      文章编号：

0 引言

多自由度永磁球面电机应用于机器人，航空航天，卫星通讯及人体关节仿生等需要精确定位的多自由运动领域[1-6]。传统的多自由度电机机械轴承的支撑结构复杂[7-8]，磨损问题严重，實用性低，而考虑液质悬浮机理的多自由度永磁球面电机采用润滑支撑结构，在流体动力动力润滑条件下，定子与转子间隙内形成一层动压油膜，使定子、转子隔离，并支撑负载，能实现高精度定位，驱动灵活，无摩擦运行，耗能低，同时还具有除锈、缓冲减振和降噪的作用，因此，球面轴承的润滑性能对电机的稳定运行有着至关重要的作用。

由于动力润滑的优良性能，研究者将其应用到工作轴承上。Lijes提出一种流体膜轴承和磁轴承配置成的混合轴承，并研制了一套实验装置，对油膜轴承和混合轴承进行了实验，比较两种轴承在相同工况下的磨损结果，得知在边界润滑条件下工作的轴承的磨损可以大大降低[9]。Polyakov提出一种滚动轴承和液膜轴承的结合体，可以提高轴承的稳定性和可靠性，并利用速度分割法建立混合轴承动态特性计算和分析[10-12]。永磁球面轴承实质属于球面滑动轴承，其润滑力学计算与普通的球面滑动轴承类似。球面轴承的理论研究方面，Dowson考虑了润滑剂粘度、密度沿膜厚方向变化的情况，推导出球面轴承用于Newton流体的Reynolds方程[13]。Tian等提出一种新的柔性多体动力学弹流润滑球形关节模型，采用逐次超松弛（ SOR ）算法求解Reynolds方程，得到球形接头的润滑压力，针对润滑油网格与套筒内表面节点网格之间存在的润滑界面不一致性问题，提出了一种新的润滑油有限差分网格旋转方案[14]。汤占岐等通过建立球面关节轴承的三维润滑模型，考虑转动、倾斜和摆动运动等因素，推导出球坐标下适用于非Newton流体润滑的Reynolds方程，分析不同的幂律指数、内圈倾斜角度及摆动角度下，脂润滑膜的压力分布、最大压力、承载力和流量[11]。何畏等考虑了球面固定套轴承的特殊结构，推导出Reynolds方程，研究偏心率、转速及轴承间隙对压力及承载力的影响[15]。

目前国内外缺少对多自由度电机这类装置的润滑轴承及其支承特性进行深入的理论分析，又鉴于在直角坐标系和柱坐标系的润滑理论不能直接应用于这类球面轴承的电机，而其流体动压润滑方程及其求解过程等问题的研究较少，为此有必要对多自由度永磁球面电机开展润滑理论方面的研究，推导出球坐标系下适用于球面轴承润滑的Reynolds方程和油膜厚度方程并进行数值求解。

1几何模型及工作原理简介

1.1结构特点

多自由度永磁球面电机结构示意图如图1所示，主要有电磁结构和球面轴承结构组成。图2（a）为电机的电磁结构示意图，在XY平面上垂直分布四极瓦状永磁体，由十字型的转轴连接，在其尾部有单极圆盘状精细调节永磁体，杆状输出轴将两部分永磁体连接固定。在永磁体外围有五个爪形空心线圈结构，分布在永磁体的上、下、左、右及其尾部。图2（b）为电机的球面轴承结构示意图，转子球壳为完整的球面，定子球壳存在球缺部分，为非完整的球面，在两个球面之间充满粘性油膜，旋转运动时形成的油膜能使得转子实现悬浮并自动定位，因此电机在运转时，转子与定子没有直接接触，最大程度上克服了摩擦对运动控制的影响，进而实现无摩擦运动。

1.2工作原理

该电机采用混合驱动模式，瓦状永磁体与其主线圈即上、下、左、右的线圈完成大范围运动，圆盘状精细调节永磁体与尾部线圈实现小范围精细位置的调节。其工作原理是电机的永磁体的磁极产生的磁场和通电空心线圈通过电生磁原理获得的磁场相互作用产生的电磁力，同极性相排斥，异极性相吸引来驱动电机完成自转及偏转运动。改变和组合定子线圈的电流大小及方向，可实现转子在各个方向的运动。

利用多物理场计算平台，对永磁体和电磁系统进行分析，如图3所示为永磁体磁极截面磁通密度分布图。永磁体的边缘部分磁通密度高于永磁体的内部，两极永磁体的磁极交界处磁通密度最大。线圈安匝数设置为300A并添加激励。首先进行线圈几何分析，再稳态计算，图4为线圈磁通密度分布图，改变空心线圈通电电流大小及方向，产生的磁场也随之改变。图5为空心通电线圈产生的磁场沿Z方向的分布图，可见在空心线圈的中心最近处磁场强度最大，随着Z值越大，磁场强度逐渐递减。图6为四个空心线圈的磁场流线分布图，增加线圈的个数能够提高磁场的均匀性。

2液体油膜润滑理论分析

以球面电机为研究对象，在球坐标系下推导出球面雷诺方程和油膜厚度方程来进行研究。解析法很难计算出来，基于数值计算方法的流行，利用有限差分法编程求解。由多自由度电机结构并结合分析条件，简化为[16-17]：

1） 忽略油膜的质量，不存在重力和惯性力;

2） 油膜在接触的边界面上没有相对滑动;

3） 油膜液体为牛顿流体;

4） 不计油膜厚度方向上的密度的变化;

2.1雷诺方程的推导

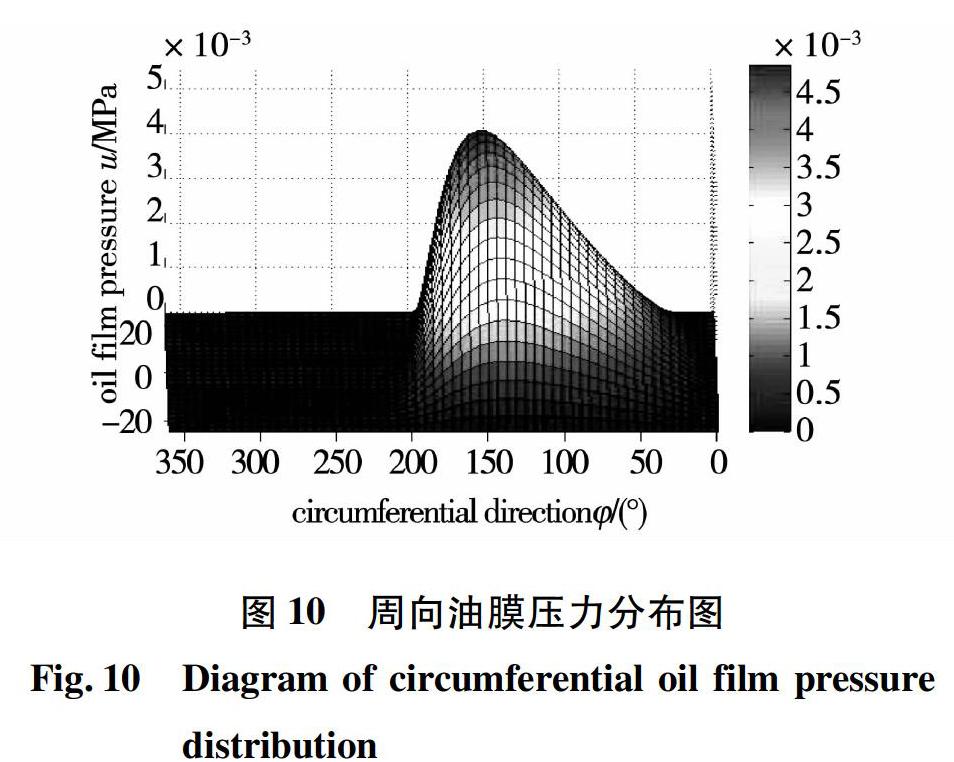
图10为周向油膜压力分布曲线图，可知在 至 的区域上，油膜压力逐渐增大到最大压力值后急剧下降，在 的某一区域，油膜压力几乎突变为零，此时油膜发生了自然破裂，这符合楔形油膜的变化情况。对此，可做如下解释：起初在最大油膜间隙处，由于压力梯度的作用，油膜压力逐渐增大， ，直到压力达到最大值， 随后压力逐渐减小， 在最小间隙处后间隙空间开始增大，由压力梯度引起的油膜流动能够充满增大的空间，从而使压力流动消失。

4.3偏心率对润滑性能的影响

定、转子的偏心率取值如表2所示，利用控制变量法，得到不同的偏心率下产生的不同油膜压力，再根据最大压力值所在的点得到周向压力分布和轴向压力分布，如图11（a）和（b）所示。在偏心率不同的情况下，润滑油膜的最大压力分布曲线形状相同，变化规律也相同。随着周向和轴向偏心率的增大，压力峰值增大，压力分布曲线所包围的面积也相应的增大，所以润滑油膜的平均压力值也增大，承载能力也增强。

由图11（c）可知，偏心率和电机转速的改变，反应了转子偏离了静平衡位置，发生不同速度的变位运动时油膜压力的相应变化情况，随着电机周向偏心率、轴向偏心率和转速的增加，楔形间隙间存在的压力差也增大，油膜需要提供足够大的承载力平衡外载荷，以避免定转子表面摩擦，摩擦越小电机寿命越长。

4.4定转子间隙对润滑性能的影响

电机定转子间隙相对直径来说较小，但其直接影响电机运行状况。电机以不同的速度运转，定转子间隙在改变，油膜厚度也相应变化，进而影响油膜压力分布，为了能很好地说明定转子间隙对润滑性能的影响。以定转子间隙分别取值为0.35， 0.40， 0.45， 0.50， 0.55 mm时，保证其他参数不变时，分别计算出这五种情况下油膜的最大压力值和承载力。如图12所示，将其结果做成曲线以便于观察其变化规律，油膜压力与定转子间隙成反比关系，电机转速一定时定转子间隙越小，油膜的压力越大，承载能力越强。转速增加，间隙减小时，油膜压力最大。这是由于电机转动时，不断地把油膜带入收敛的楔形间隙中，油膜受到压迫就产生抗力，来平衡外载荷，间隙越小，油膜越薄，其承载力越大。但油膜厚度不能太小，若其承受的最大压力超过电机对油膜的压力，容易使油膜发生震荡而失稳，所以选取合适的定转子间隙是至关重要的。

4.5速度系数Λ对油膜承载力的影响

速度系数Λ是一个综合参数，是由油膜黏度，供油压力，转速和定转子间隙等电机参数共同作用的结果。取速度系数Λ分别为0.08， 0.12， 0.241， 0.29時，得到不同的偏心率下油膜的承载力如图13所示。当Λ=0时，油膜承载力也为0，这是由于此时电机转速为0，油膜的状态没有发生任何改变而无压力产生。而在电机偏心转动时，油膜由收敛间隙的大端向小端流动，形成流体动压力。在其它参数不变时，油膜承载力随着速度系数Λ增加而明显增强，二者成正比关系。在速度系数Λ相同时，增加周向和周向偏心率，油膜承载力增加的幅度逐渐加大。这是因为在偏心率没有达到最小临界值时，电机转动形成的动压效果随着偏心率增大而增强。

4.6 油膜粘度對润滑性能的影响

电机的原型如图14所示，样机结构包括圆柱定子线圈、转子永磁体、转矩传感器、驱动器、计算机、外壳和底座。为了方便测量输出转矩，输出轴与转矩传感器相连，经检测获得频率信号，由频率计显示直接送计算机处理。

在润滑介质的特性参数中，粘度是表示液体粘滞程度的一项最重要的质量指标，也是影响润滑特征的关键参数[23-24]。在电机运行一段时间后会有能量损耗转化成热量，且热量不能完全耗散掉，造成电机温升，而润滑油作为球面轴承的润滑介质，其粘度受温度和时间变化的影响非常大，因此搭建了实验装置，采用旋转法测量润滑粘度特性。

如图15为润滑油粘温实验装置，主要包括旋转式黏度计、红外线测温仪、水浴加热器、永磁球面转子、润滑油等。采用恒温水浴加热器对润滑油进行加热至所设定的温度，同时利用旋转式粘度计测量其粘度，采集获得初始粘度数据。然后选择转子球面轴承和合适的转速测量运行 后的润滑油粘度。通过采集润滑油在一定的时间后，其温度变化时的粘度数据，绘制了润滑油在永磁球面转子随时间变化的粘温特性曲线，如图16所示，其中包括了转子运行 后润滑油粘度所测值和初始时所测值，比较可知运行 后润滑油粘度高于初始粘度，随着温度升高都呈现出急剧下降的趋势，且在低温区粘度下降更为明显，高温区两曲线差距很小，几乎重合。

通过以上试验可知运转时间及温度对转子球面轴承润滑油粘度的影响，实际工况下的球面轴承润滑油在运转一定时间后的粘度特性的变化规律对润滑理论分析具有重要的意义。由此分别对五种不同粘度为0.023、0.033、0.043、0.053、0.063Pa.s的润滑油产生的油膜压力进行数值计算。图17表明油膜粘度越低，转速越慢时，油膜的压力越小。这是由于电机运转过程中，油膜粘度会降低，而油膜粘度的降低会使油膜厚度变薄，造成油膜的抵抗能力也减弱，降低了油膜的压力及承载能力，易引起局部油膜破坏和表面磨损，润滑失效，甚至发生润滑油碳化，从而影响电机的润滑性能。

5 结论

（1） 通过对该电机建模与分析其工作原理，得到转子永磁体可产生稳定的磁场和多个爪形定子线圈的能够产生均匀的磁场，两磁场相互作用驱动电机运转。

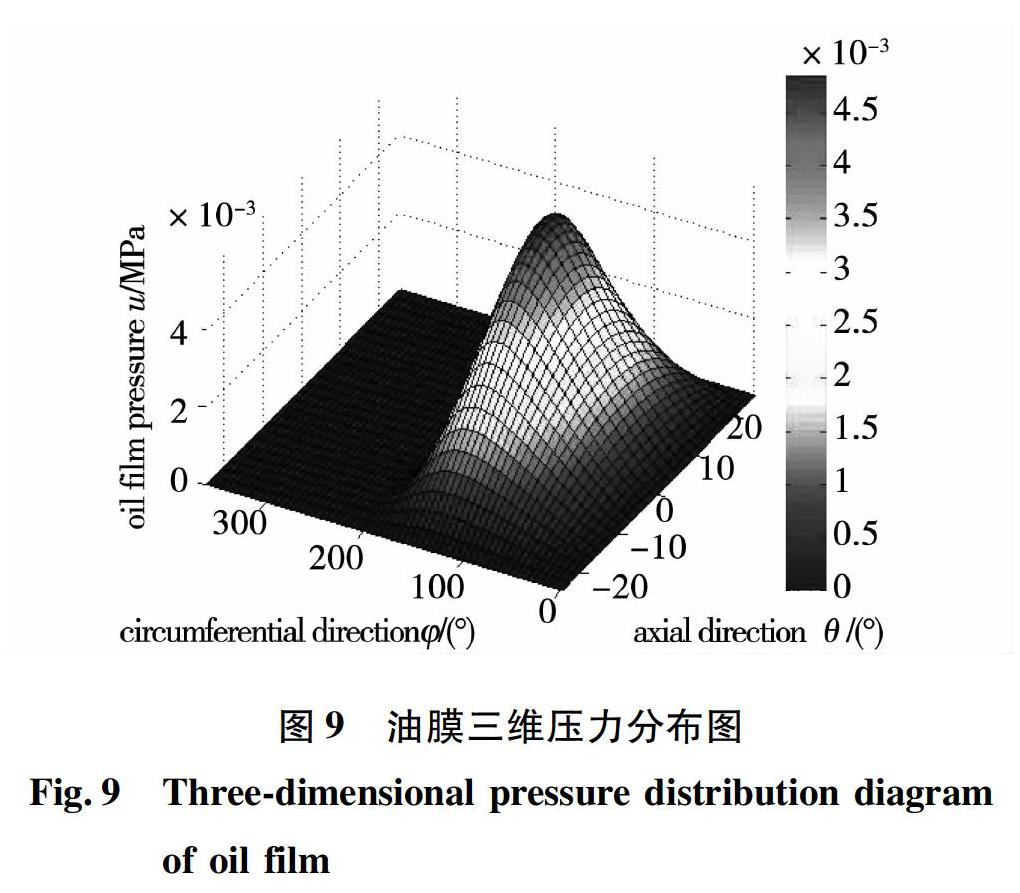
（2） 利用微元体分析方法，依据动量和能量守恒推导出球面电机润滑油膜条件下的Reynolds方程，并忽略微小项等进行一系列化简，结合周向和轴向偏心率的膜厚方程，通过有限差分法、数值编程计算得到油膜压力分布图，并从理论上揭示了偏心率、定转子间隙、电机转速、速度系数Λ及油膜黏度与油膜压力及承载力的关系，并通过实验获取润滑油在不同运转时间的黏温特性曲线图。

（3） 在合适的润滑条件下，多自由度电机润滑油膜能够产生流体动压润滑，压力分布合理，符合多自由度电机实际情况。

（4） 在油膜厚度没有达到最小临界值时，增大周向偏心率、轴向偏心率、电机转速、油膜黏度及速度系数，减小定转子间隙，都会引起油膜压力和承载力的增大，从而提高油膜承载能力，使参数保证在合适的范围内，优化考虑液质润滑球面轴承的多自由度永磁电机结构设计，延长使用寿命，为电机工作中球面轴承的润滑性能分析和安全运行提供参考。

参考文献：

[1] 李争，王群京.永磁多维球形电动机的研究与发展现状[J].微特电机， 2006，33（10）： 7-11.

LI Zheng， WANG Qunjing. The present research and development situation of permanent magnet spherical motor of multi-dimensions[J]. Small & Special Electrical Machines， 2006， 33（10）： 7-11.

[2] 李争， 聂雅盟， 薛增涛， 等. 液质悬浮式三自由度电机电磁特性的计算分析[J].电机与控制学报， 2017， 21（4）： 44-52.

LI Zheng， NIE Yameng， XUE Zengtao， et al.Calculation and analysis of electromagnetic properties of liquid-suspended three-degree-of-freedom motor [J] .Electric Machines and Control， 2017， 21 （4）： 44-52.

[3] 李争，孙克军，王群京，等.一种多自由度电机三维磁场分析及永磁体设计[J]. 电机与控制学报， 2012， 16（7）： 65-71.

LI Zheng， SUN Kejun， WANG Qunjing， et al. 3D magnetic field analysis and permanent magnet design of a Multi-degree-of-freedom motor[J]. Electric Machines and Control， 2012， 16（7）： 65-71.

[4] Z. LI， D. H. XING. Analysis of magnetic field and oil film characteristics of a novel hybrid drive multi-degrees-of-freedom permanent magnet motor[C]. IEEE International Conference on Industrial Electronics and Applications， 2016： 239-244.

[5] B. Li， G.D. Li， H.F. Li. Magnetic Field Analysis of 3-DOF Permanent Magnetic Spherical Motor Using Magnetic Equivalent Circuit Method[J]. IEEE Transactions on Magnetics， 2011， 47（8）： 2127-2133.

[6] 李争. 一种液质悬浮式仿生电磁驱动三自由度运动电机， CN104617691A[P]. 2015.

[7] 张文，郑晓钦，吴新振.多相感应电机三维电磁分析与损耗计算[J].电工技术学报， 2018， 33（S2）： 331 - 337.

Zhang Wen. Zheng Xiaoqin. Wu Xinzhen. Three-Dimensional Electromagnetic Analysis and Loss Calculation of Multiphase Induction Motor[J]. Transactionsof China Electrotechnical Society， 2018， 33（S2）： 331-337.

[8] 李立毅，张江鹏，闫海媛，于吉坤.高过载永磁同步电机的电磁特性[J].电工技术学报， 2017， 32（02）： 125 - 134.

Li Liyi. Zhang Jiangpeng. Yan Haiyuan. Yu Jikun. Electromagnetic Characteristics of High Overload Permanent Magnet Synchronous Motor[J]. Transactions of China Electrotechnical Society， 2017， 32（02）： 125 - 134.

[9] Lijesh K P， Hirani H. Design and development of permanent magneto-hydrodynamic hybrid journal bearing[J]. Journal of Tribology， 2017， 139（4）： 044501-9.

[10] 王小飞，代颖，罗建.基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报， 2019， 34（S1）： 22 - 29.

Wang Xiaofei. Dai Ying. Luo Jian. Design and Temperature Field Analysis of Vehicle Permanent Magnet Synchronous Motor Waterway Based on Fluid-solid Coupling[J]. Transactions of China Electrotechnical Society， 2019， 34（S1）： 22 - 29.

[11] Polyakov R. Interaction of rolling-element and fluid-film bearings dynamic characteristics in hybrid bearings[J]. Procedia Engineering， 2017， 206：61-67.

[12] Dowson D. A generalized Reynolds equation for fluid-film lubrication[J]. International Journal of Mechanical Science，1962， 4（2）： 159-170.

[13] Tian Q， Lou J， Mikkola A. A new elastohydrodynamic lubricated spherical joint model for rigid-flexible multibody dynamics[J]. Mechanism & Machine Theory， 2017， 107：210-228.

[14] 汤占岐， 刘焜， 王伟，等. 转动与摆动复合运动下脂润滑关节轴承的数值分析[J]. 应用数学和力学， 2015， 36（2）：207-219.

Tang Zhanqi， Liu Xun， Wang Wei， et al. Numerical analysis of grease-lubricated joint bearings with combined rotation and swing[J]. Applied Mathematics and Mechanics， 2015， 36 （2）： 207-219.

[15] 何畏， 贺军超， 熊尉伶， 等. 新型球面固定套轴承球坐标润滑理论研究[J]. 润滑与密封， 2016， 41（10）：62-67.

HE Wei， HE Junchao， Xiong Weiling， et al. Study on the ball-point lubrication of a new spherical plain bearing [J]. Lubrication and Seal， 2016， 41 （10）： 62-67.

[16] M. A. REZVANI， E. J. HAHN. Floating ring squeeze film damper： Theoretical Analysis. Tribology International， 2000， 33 （3-4）： 249-258.

[17] 邢殿輝. 液质悬浮式混合驱动多自由度永磁电机的设计与分析[D]. 河北科技大学， 2016.

Xing Dianhui. Design and analysis of liquid-suspended suspension hybrid multi-degree-of-freedom permanent magnet motor [D]. Hebei University of Science and Technology， 2016.

[18] 楊金福， 刘占生， 解永波， 等. 关于Reynolds方程求解的动态边界条件研究[J]. 黑龙江电力， 2004， 26（5）： 346-349.

Yang Jinfu， Liu Zhansheng， Xie Yongbo， et al. Study on dynamic boundary conditions for solving Reynolds equation[J]. Heilongjiang Electric Power， 2004， 26 （5）： 346-349.

[19] 杨沛然. 流体润滑数值分析[M]. 北京： 国防工业出版社， 1998.

YANG Peiran. Numerical Analysis of Fluid Lubrication[M]. Beijing： National Defense Industry Press， 1998.

[20] 张文涛， 马腾， 等. 基于CFD的新型斜面推力滑动轴承承载性能分析[J]. 润滑与密封， 2017（9）：70-75.

Zhang Wentao， Ma Teng， et al. Analysis of bearing performance of a new inclined thrust sliding bearing based on CFD[J]. Lubrication Engineering， 2017（9）： 70-75.

[21] 王宁. 基于MATLAB的滑动轴承压力分布的数值计算[D]. 大连理工大学， 2006.

WANG Ning. Numerical calculation of pressure distribution in sliding bearing based on MATLAB [D]. Dalian University of Technology， 2006.

[22] 谢帆， 荆建平， 万召， 等. 基于有限差分法的径向滑动轴承油膜压力分布计算[J]. 润滑与密封， 2012， 37（2）：12-15.

Xie Fan， Jing jianping， Zhao， et al. Calculation of oil film pressure distribution of journal bearings based on finite difference method [J]. Lubrication and Seal， 2012， 37（2）： 12-15.

[23] 康建峰， 王建梅， 马立新， 等. 油膜轴承油润滑性能试验研究[C]. 全国摩擦学大会， 2013.

Kang Jianfeng， Wang Jianmei， Ma Lixin， et al. Experimental research on oil lubricated performance of oil film bearings [C]. National Tribology Conference， 2013.

[24] 张亚南， 王建梅， 张艳娟， 等. 时间累积效应对油膜轴承油粘度的影响研究[J]. 太原科技大学学报， 2016（1）：64-67.

Zhang Yanan， Wang Jianmei， Zhang Yanjuan， et al. Effect of time cumulative effect on the oil viscosity of oil film bearings[J]. Journal of Taiyuan University of Science and Technology， 2016（1）：64-67.