基于半参数时间序列模型的我国人均国内生产总值的预测研究

王明辉

一、引言

将一个国家核算期内（通常是一年）实现的国内生产总值与这个国家的常住人口（或户籍人口）相比进行计算，得到的人均国内生产总值（人均GDP），不仅是衡量各国人民生活水平的重要标准，而且是人们了解和把握一个国家的宏观经济运行状况的有效工具，常作为经济学中衡量经济发展状况的指标，是最重要的宏观经济指标之一。特别是从2010年起，我国GDP总量超越日本位居世界第二后，主流意识都逐渐强调起人均GDP的重要性，这是一种必要的戒骄戒躁、理性清醒和自觉，因为我国的人均GDP和发达国家相比差距还很大，要认识到“第二大”并不等于“第二强”。所以，较为精确地分析并预测人均GDP的变化趋势是非常有必要的。

在过去的70多年里，时间序列分析，尤其是线性时间序列ARIMA模型[1]发展迅速、成果丰富。其研究日趋成熟，并得到广泛且非常成功的应用。然而在很多领域，例如在经济、金融、环境、气象和生物等诸多领域，存在着大量涉及非线性时间序列的问题，用线性时序分析方法去研究和解决这些问题，易丢失信息，效果欠佳。经验表明，非线性时间序列分析方法在这些领域已经取得成功的应用。非线性时间序列，哪怕是很简单的非线性时间序列，都能显示出奇异的现象，足以令人新奇不已。况且，非线性时间序列分析与许多非线性科学领域有着密切的联系，例如与混沌、分形和神经网络等领域均有密切的关系。这也说明非线性时间序列能表现出更丰富、更复杂的客观现象，比线性时间序列有着更广阔的应用前景，能解决许多复杂的实际问题。事实上，在很多领域，已经显示出非线性时间序列分析的应用前景。因此，近年来对非线性时间序列分析的研究受到广泛关注[2]。

研究非线性时间序列，很难仿效或沿用已有的线性时间序列的理论与方法，而且所面临的困难也远远超过线性情况。正像在其他非线性科学领域一样，人们遇到了许多新的激动人心的挑战。常见的处理非线性关系的方法有数据转换方法和神经网络、支持向量机、投影寻踪和基于树的方法等高计算强度方法。然而，这些方法要么在实际使用过程中有很大的局限性，要么得到的结果无法解释。使用半参数模型来模拟非线性关系则在一定程度可以避免这些问题。

半参数模型是二十世纪八十年代发展起来的一类重要的统计模型。这类模型由于引入了表示模型误差或其他系统误差的非参数分量，因而既含有参数分量，又含有非参数分量，兼顾了参数模型和非参数模型的优点，较之参数模型或非参数模型有更大的适应性，也具有更强的解释能力，同时又可避免许多“维数灾难”问题。

因此，本文采用1978～2016年的人均GDP数据，尝试建立半参数时间序列模型，通过分析其变化特征，预测未来三年的数值，并给出其95%的置信区间，以期对现有模型进行一定程度的扩充，同时给未来的研究者提供一定的借鉴意义，也可为促进经济更好更快地发展提供参考依据。

二、半参数时间序列模型

半参数时间序列模型是一类非线性时间序列模型的统称，包括可加、单指标和变系数等模型，其中一种较为简单的模型为具有自回归误差项的部分线性模型。Yu等[3]对于具有独立同分布误差项的自回归模型，假定回归函数来自某个参数分布族，使用条件最小二乘方法得到参数估计后，再运用非参数核方法进行调整，最后证明了回归函数估计量具有弱相合性。Farnoosh和Mortazavi[4]则将该方法运用到具有一阶自相关误差项的自回归模型中。Farnoosh等[5]研究了具有独立同分布误差项的部分线性自回归模型中回归函数的半参数估计和性质。

本文主要采用具有一阶自回归误差项的部分线性模型：

三、人均GDP的实证分析

1.数据预处理

图1 人均GDP时序图

本文主要研究1978～2016年的人均GDP（1978年=100），原始数据Yt来源于《中国统计年鉴—2017》，对于=Yt/1000绘制时序图。

图2 一阶差分序列时序图

从图1可看出该序列在这39年间呈曲线增长趋势，显然非平稳，一阶差分后的时序图见图2，仍显示不平稳，但二阶差分后在显著性水平0.05下，变为白噪声序列，因此不适合采用ARIMA模型进行拟合。

2.模型建立

取 g（x，θ）=θex，采用上节所述方法建立具有一阶自回归误差项的部分线性时间序列模型，所得拟合方程如下：

图3 的真实值（实线）与估计值（虚线）对比

3.模型检验

对参数进行显著性检验，结果显示在表1中，因此在0.05的显著性水平下，三个参数均显著。

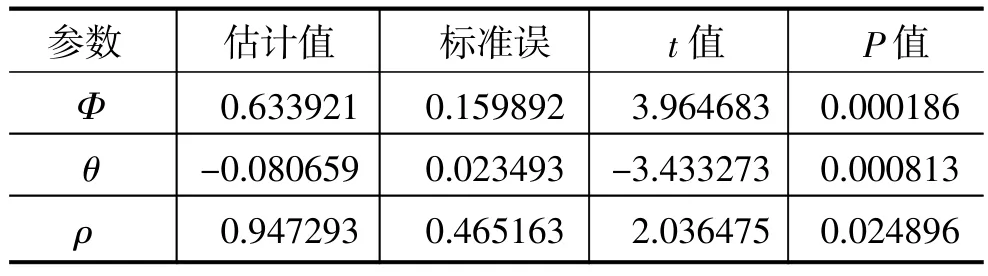
表1 参数显著性检验结果

图4 残差序列Q-Q图

图4为残差序列的Q-Q图，用来描述残差序列是否服从正态分布。图中的数据点基本上按照对角直线排列，趋于一条直线，并被对角直接穿过，且有95%的样本点落在[-2，2]值区间内，故应认为残差序列近似服从正态分布。再加上采用Shapiro-Wilk正态性检验方法，所得统计量的值为0.9682，对应的P值为0.3618，更加印证了残差序列具有正态性。两者从侧面反映了本节方法的拟合效果。

4.模型预测

利用上节模型预测2017～2019年的，并还原为人均GDP，所得结果见表2，同时给出它们的95%置信区间，预测结果延续了该序列的增长趋势，2019年的数据将突破3000，会是1978年的30倍。

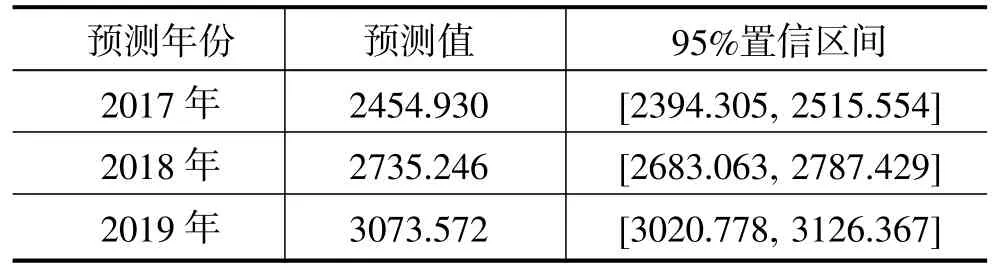
表2 2017～2019年的预测值

5.与其他模型的比较

前面已经做过分析，该人均GDP序列不适合采用ARIMA模型进行拟合，为了说明本文方法的可行性，我们采用二次回归、三次回归、指数回归和幂模型进行建模，各方法所对应方程如下：

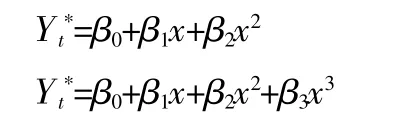
表3列出了本文所用方法与其他方法的参数估计和模型汇总。经过显著性检验，发现上述模型的拟合方程均在0.05的显著性水平下显著，同时模型残差也能通过正态性检验。只有两个参数在该显著性水平下不显著，删除这两个参数后的拟合方程也包含在表中。与其他方法相比，本文采用的方法拟合效果较好，具有一定的优越性。

四、结语

本文以我国人均GDP为研究对象，利用1978～2016年的数据，通过建立半参数时间序列模型分析其变化特征，并预测了未来三年的数值，给出了其95%的置信区间。该方法不仅是对现有模型的扩展，而且具有一定的参考价值和实用价值。

不可否认，该建模方法也存在一定的难点和不足。首先，模型的定阶存在一定难度，即Yt和ut滞后阶数的确定暂时没有较为完善的方法。其次，参数分布族{g（x，θ）；θ∈Θ}的确定也具有一定的难度，且直接影响模型的拟合效果。这些难点都对研究者提出较大挑战，需要其较为准确地把握数据本身的趋势，这将是我们下一步的研究重点。

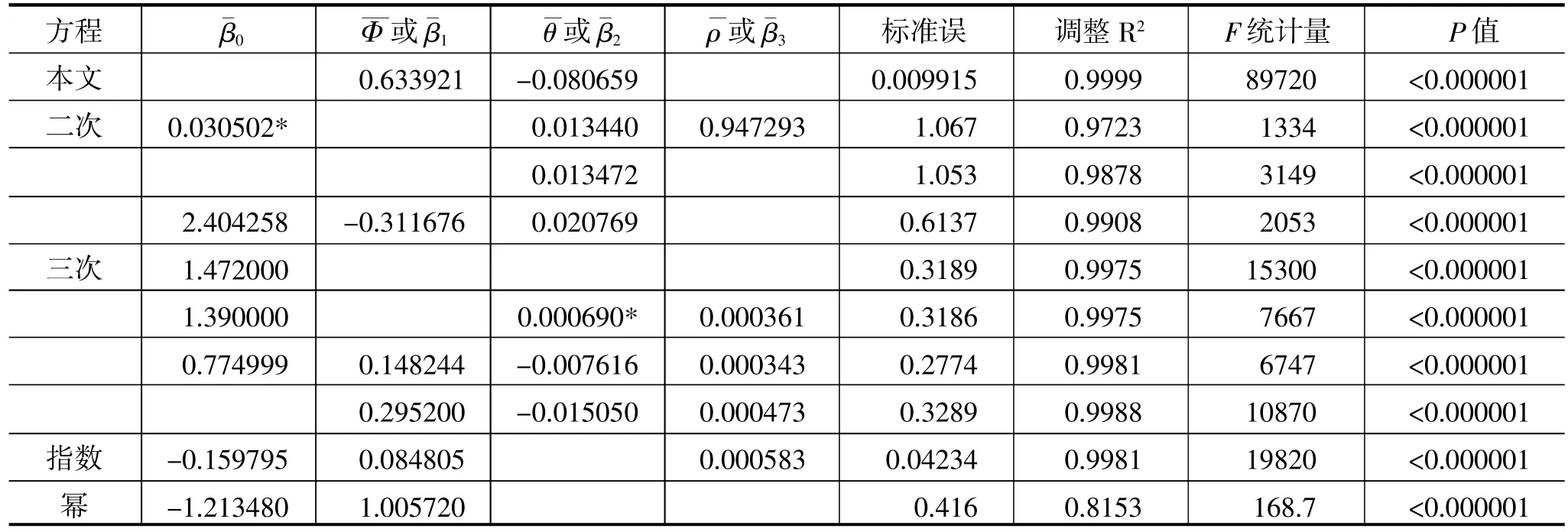
表3 参数估计和模型汇总