喷丸强化对Ti6Al4V半椭圆表面裂纹J积分和裂纹扩展速率的影响

侯 帅，朱有利，邱 骥，倪永恒

(陆军装甲兵学院 装备保障与再制造系，北京 100072)

喷丸强化是使材料表面发生循环塑性变形的过程，在表层形成残余压应力的同时改善组织结构，达到提高构件抗疲劳性能的目的。喷丸强化被广泛应用于航空、军工和汽车等领域[1-3]，而且随着对机动性和疲劳可靠性要求的不断提高，其应用受到越来越多的关注，除了对喷丸强化工艺和设备的不断改进之外，对喷丸强化构件的寿命评估也成为领域内的研究热点和重点之一。但目前对喷丸强化件的寿命评估主要依赖于疲劳实验，这不仅耗时、费力，而且实验结果的离散性较大，特别是定量评估喷丸强化层对疲劳裂纹扩展寿命的作用，目前尚缺乏有效的方法。因为评估裂纹扩展寿命需要计算或测量裂纹前沿的J积分或应力强度因子等断裂力学参量，但由于喷丸强化层较浅，很难制备标准CT试件，因此很难通过实验方法测量喷丸强化层的J积分，这也是目前在设计阶段考虑喷丸强化层对扩展寿命作用的主要困难之一。采用断裂力学方法计算喷丸强化对裂纹前沿J积分的影响是一种可行的方法，但目前这种方法主要是基于线弹性断裂力学理论，将残余应力与外载荷单独作用下的应力强度因子进行线性叠加[4-6]。残余应力主要有两种方法获得，一是采用X射线衍射剥层测量法，二是喷丸残余应力分布的拟合方法。Gao等[7]采用XRD法获得喷丸残余应力沿深度的分布曲线，然后采用权函数法计算了单边缺口拉伸试样的应力强度因子。吕鹤婷等[8]采用Robertson公式[9]拟合喷丸残余应力分布曲线，建立二维四点弯曲有限元模型，计算了裂尖应力强度因子并考虑了裂纹闭合效应。Liu等[10]建立了二维内聚力有限元模型，拟合文献中的喷丸残余应力，计算了循环载荷下裂尖应力强度因子。上述研究方法仅拟合了喷丸后的残余应力分布，而未考虑喷丸强化所形成的加工硬化(塑性变形)和残余应变能，而且简化为二维问题忽略了喷丸残余应力的复杂性，这势必带来对裂纹前沿断裂参数计算的误差。而存在喷丸残余应力、残余应变和残余应变能的情况下，传统J积分的计算不再具有路径无关性，因此不能作为断裂参数使用。Lei等[11]提出了在不计体力和裂纹面力条件下修正的J积分计算公式，并证明了其路径无关性，在该公式中考虑了残余应力、残余应变和残余应变能等参量。

本工作首先对喷丸强化工艺进行三维有限元建模仿真，并通过改变约束条件生成疲劳裂纹并施加远场载荷，然后采用修正的J积分计算公式，在考虑喷丸残余应力、残余应变和残余弹性应变能的条件下定量计算半椭圆表面裂纹的J积分值和裂纹扩展速率，考察喷丸工艺和裂纹深度对上述断裂参量的影响，为定量评估喷丸强化层对疲劳裂纹扩展寿命的作用提供计算方法。

1 修正的J积分

J积分的概念由Rice[12]提出：

(1)

式中：W为裂纹体的应变能密度；σij为作用在弧元ds上的应力张量；uj为弧元ds上点的位移矢量；δij为Kronecker记号；ni为弧元ds外法线的方向余弦；Γ为围绕裂尖曲线，起始于裂纹下表面，沿逆时针方向(弧元ds正向)止于裂纹上表面。

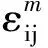
(2)

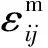
(3)

(4)

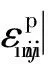
(5)

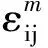
(6)

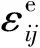
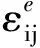
(7)

W=Wt-Wp|ini

(8)

式中：Wt为总应变能密度；Wp|ini为初始状态中的塑性功密度。

2 喷丸与三维半椭圆表面裂纹有限元模型

几何模型及参数为：靶材的长、宽、厚分别为x=10mm、y=6mm、z=3mm，对称面建立半椭圆表面裂纹，裂纹半长c=1mm，建立4种深度分别为0.3，0.5，0.8，1.0mm的裂纹(半椭圆表面裂纹最大深度记为a),以研究喷丸强化层对含不同深度裂纹结构的影响。

靶材材料为Ti6Al4V，弹性模量112GPa，泊松比0.34，密度4430kg/m3，采用双线性随动强化模型，屈服强度860MPa，硬化模量200MPa[15]。丸粒为刚体(采用R3D4单元划分网格)，直径0.8mm，密度7800kg/m3，初速度分别为25，30，40m/s。为均匀覆盖含裂纹区域使用了31个丸粒，喷丸覆盖率约为100%。丸粒与靶材表面的摩擦因数为0.2[16]，裂纹面之间的相互作用(引入裂纹后)设为硬接触(hard contact)[17]。接触状态的跟踪采用小滑动(small sliding)方法，接触算法采用罚函数法。

裂纹前沿第1层单元采用含有1/4节点的楔形奇异单元(C3D6)，裂纹前沿的第2环至第7环采用线性六面体单元(C3D8)，其他部分采用四面体单元(C3D4)，有限元模型网格划分如图1(a)所示。由于喷丸区域应力应变梯度较大，为保证计算精度，进行了网格细化，见图1(b)，网格尺度约为0.005mm。计算过程：(1)采用显式动力学算法仿真喷丸过程，约束底面Z=0上节点所有自由度，采用绑定约束来约束两个裂纹面节点自由度，弹丸参考点给定初速度。(2)采用隐式算法仿真卸载过程，复制模型，删除弹丸，保持其余边界条件不变，通过ABAQUS的预定义场进行数据传递，导入上一步计算的应力和应变等，分析步改为静态分析，采用隐式算法计算喷丸后的平衡状态。(3)引入裂纹，删除对底面Z=0上节点的约束，约束Y=0面上节点的所有自由度，删除裂纹面节点的绑定约束，计算平衡状态，并将这一状态作为初始状态。(4)施加远场拉伸载荷，在Y=6的表面节点上施加750MPa拉伸载荷，并采用式(3)计算裂纹前沿的J积分。为进行对比分析，对相同的半椭圆表面裂纹和远场载荷，采用式(1)计算未经喷丸强化处理的裂纹前沿J积分值。

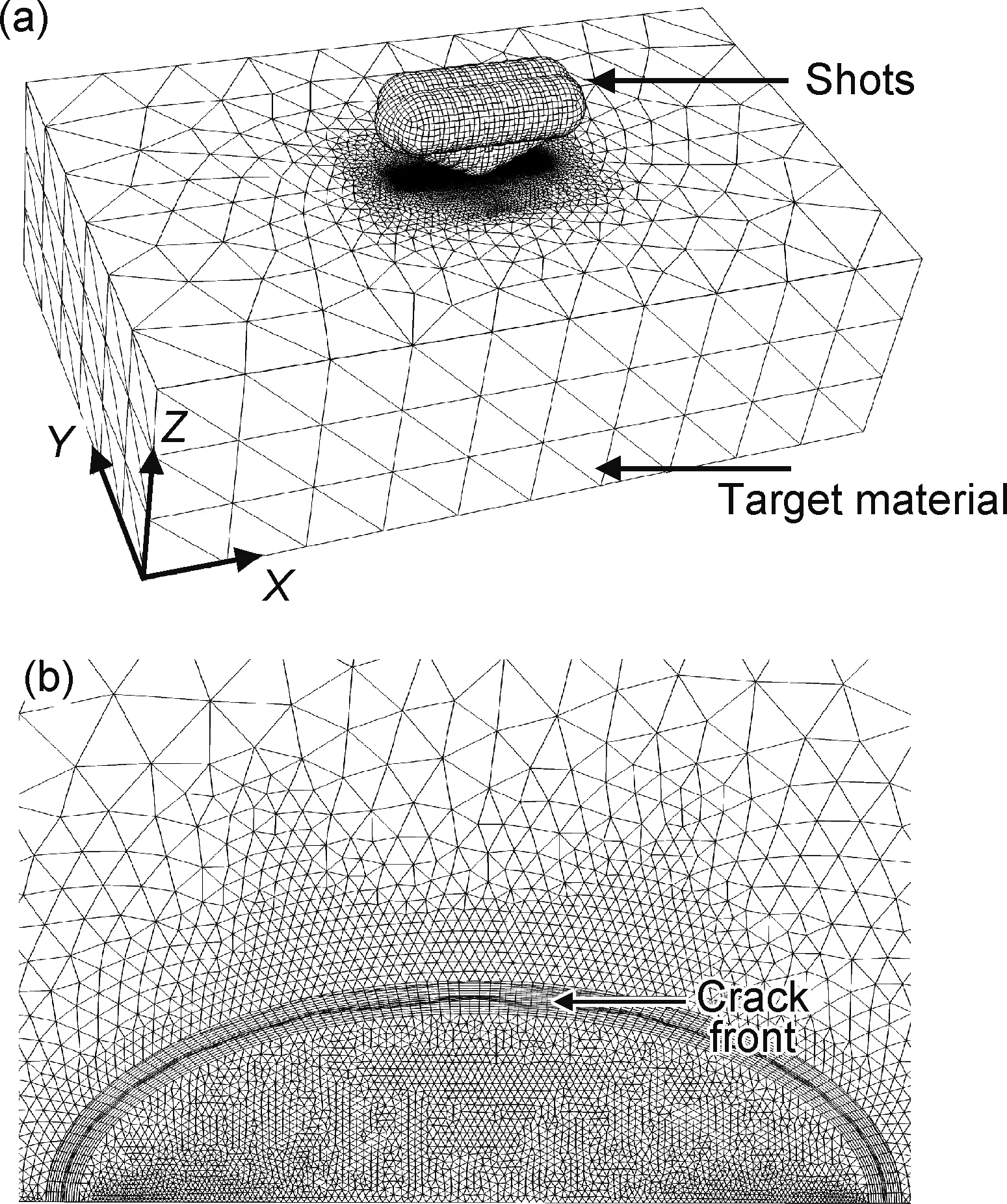
图1 喷丸有限元模型网格划分(a)与裂纹面网格细化(b)Fig.1 FEM model of shot peening(a) and mesh refinement of crack face(b)

3 结果与分析

3.1 喷丸并引入裂纹后的应力应变状态变化

以喷丸、卸载并引入0.5mm深裂纹的计算为例，得到裂纹面上的残余应力、残余应变和残余弹性应变能密度等参量，如图2所示。喷丸、卸载并引入裂纹后，距表面0.25mm的范围内为垂直于裂纹面的残余压应力σzz，超过0.25mm为残余拉应力，但在裂尖表现出较大的奇异性(图2(a))，表层产生了约0.2mm深的塑性变形层，即加工硬化层(图2(b))，弹性应变能密度影响层深约为0.22mm(图2(c))。由式(3)可知，喷丸产生材料状态(残余应力、残余应变和残余弹性应变能)变化将影响裂纹前沿断裂参数。

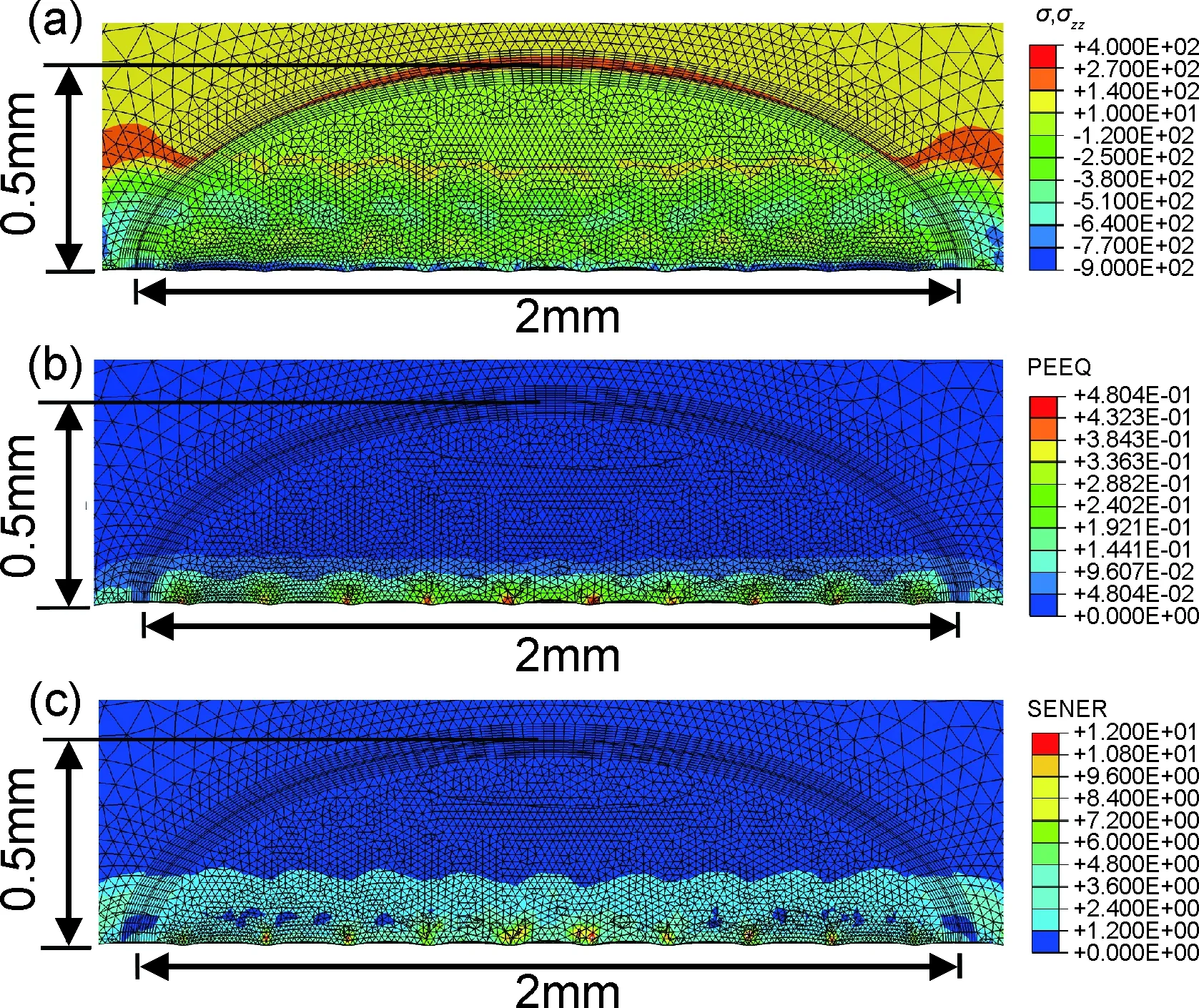
图2 喷丸并引入0.5mm深裂纹后裂纹面上各参量云图(a)垂直于裂纹面的残余应力σzz；(b)等效塑性应变；(c)弹性应变能密度Fig.2 Contour maps of three parameters after shot peening and generating 0.5mm deep crack(a)residual stress σzz perpendicular to the crack surface;(b)equivalent plastic strain;(c)elastic strain energy density

3.2 修正的J积分的路径无关性

由于裂纹尖端不可避免地会产生应力奇异性，因此靠近裂纹前沿的J积分值计算精度较差，且趋近于裂纹前沿的J积分没有物理意义[18]。另外，Brocks和Scheider认为，在小范围屈服条件下，J积分的积分域应尽可能绕过裂尖塑性区以提高数值计算精度[19]。图3是裂纹最深点的等效塑性应变云图，第5环包围整个塑性区，因此选择第5～7环进行J积分计算。图4为喷丸(丸粒初速度30m/s)强化后引入不同深度的裂纹，并施加远场拉伸载荷后由式(3)计算得到的J积分分布曲线。为便于比较，横坐标采用归一化的裂纹长度φ=Δl/L，其中Δl为裂纹上某点到裂纹表面端点的长度，L为半椭圆表面裂纹总长度。可见，对4种不同深度(0.3，0.5，0.8，1.0mm)的裂纹，第5环与第7环的J积分最大值分别相差为2.3%，3.5%，3.5%，2.9%，表明由式(3)计算的J积分值的路径相关性很小，这种误差主要源于有限元数值计算的误差。

图3 裂纹最深点的等效塑性应变Fig.3 Equivalent plastic strain at the deepest point of the crack

3.3 喷丸强化对不同深度裂纹的作用

3.3.1 喷丸强化对J积分值的影响

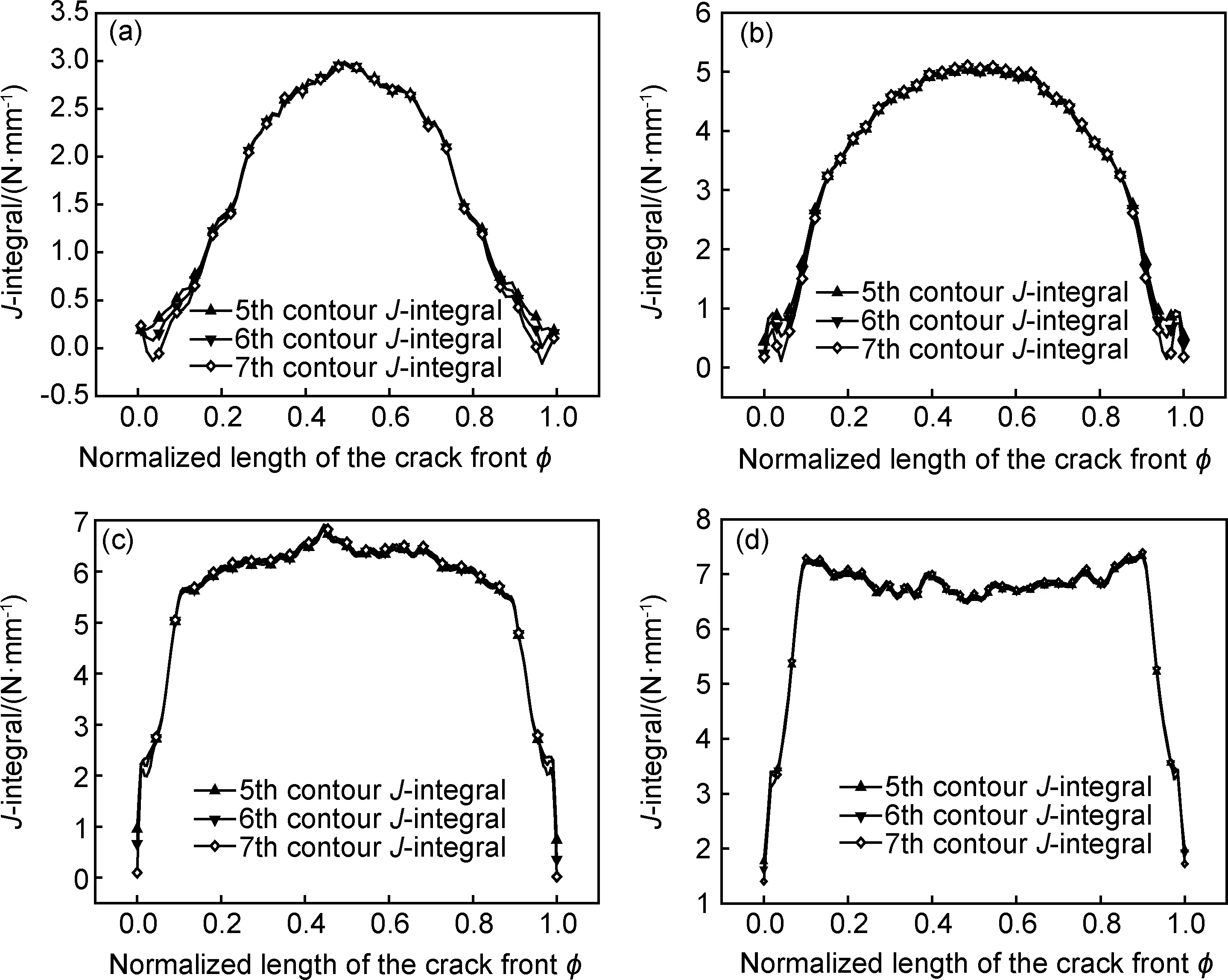
图4 喷丸强化后不同深度的J积分沿裂纹前沿的分布(a)a=0.3mm；(b)a=0.5mm；(c)a=0.8mm；(d)a=1.0mmFig.4 Distribution of the J-integral along the crack front of the different depths after shot peening(a)a=0.3mm;(b)a=0.5mm;(c)a=0.8mm;(d)a=1.0mm

图5是未喷丸和喷丸强化(丸粒初速度30m/s)后不同深度的裂纹前沿J积分计算结果。裂纹较浅时，J积分最大值位于裂纹最深点处，喷丸件的J积分值分布曲线低于未喷丸件。裂纹深度为0.3mm时(图5(a))，裂纹最深点的J积分值由4.25N/mm降低到2.99N/mm，降幅约30.1%。裂纹深度为0.5mm时(图5(b))，降幅约9.15%。裂纹深度为0.8mm时(图5(c))，裂纹最深点的J积分值差别较小。表明在强化层内时喷丸后J积分值的降幅随裂纹深度的增加而减小，即喷丸强化有益于抑制疲劳浅裂纹的扩展。当裂纹深度达到1.0mm时，疲劳危险点转移到裂纹两端，此时，紧邻表面的裂纹两端仍处于强化层内，喷丸后J积分最大值降低约9.3%，如图5(d)所示。

3.3.2 喷丸强化对裂纹前沿应力分量的影响

图6为喷丸件与未喷丸件裂纹前沿的正应力分量。与未喷丸件相比，裂纹两端(靠近近表面)的正应力分量降幅较大，裂纹最深点处应力分量的降幅较小。对于0.3mm深的裂纹(图6(a))，喷丸强化后裂纹前沿最深点处3个正应力分量σrr，σθθ，σzz的降幅分别为23.3%，12.3%，9.0%。裂纹深度增大到0.8mm时(图6(c))，喷丸强化后裂纹前沿最深点处σrr，σθθ，σzz的降幅分别为4.2%，2.7%，2.2%。当裂纹深度达1mm时(图6(d))，喷丸强化后裂纹前沿最深点处正应力与未喷丸件差别很小，但裂纹两端降幅仍较大。表明喷丸强化使裂纹前沿应力水平降低，这有益于提高结构的抗疲劳性能。

图5 喷丸件与未喷丸件裂纹前沿J积分(a)a=0.3mm；(b)a=0.5mm；(c)a=0.8mm；(d)a=1.0mmFig.5 J-integral along the crack front of shot peening and non-shot peening(a)a=0.3mm；(b)a=0.5mm；(c)a=0.8mm；(d)a=1.0mm

图6 喷丸件与未喷丸件裂纹前沿的正应力分量(a)a=0.3mm；(b)a=0.5mm；(c)a=0.8mm；(d)a=1.0mmFig.6 Normal stress distribution along the crack front of shot peening and non-shot peening(a)a=0.3mm；(b)a=0.5mm；(c)a=0.8mm；(d)a=1.0mm

3.3.3 喷丸强化对裂纹扩展速率的影响

在平面应变条件下，应力强度因子K可由J积分计算得到：

(9)

式中：E为弹性模量；ν为泊松比。

由Paris公式[21]，可得到裂纹扩展速率da/dN：

da/dN=C(ΔK)m

(10)

式中：ΔK为应力强度因子幅。疲劳载荷受应力比R=0，最大应力σmax=750MPa，Ti6Al4V材料的疲劳裂纹扩展参数[21]：C=1.681×10-10，m=2.6。应力强度因子幅度门槛值[22]ΔKth=5.37MPa·m1/2。

裂纹扩展条件为：

ΔK>ΔKth

(11)

丸粒初速度30m/s，由式(9)和式(10)计算得到裂纹前沿最大裂纹扩展速率，如表1所示。可见，裂纹深度较浅时，喷丸后裂纹扩展速率显著降低，特别是裂纹深度为0.3mm时，给定载荷下的裂纹最大扩展速率降幅约为36.7%。随着裂纹深度的增大，喷丸强化抑制裂纹扩展的作用降低。裂纹深度达到0.8mm时，裂纹扩展速率差别较小。当裂纹扩展到1.0mm深时，最大J积分值(疲劳危险点)转移到裂纹两端，该处仍处于喷丸强化层内，裂纹最大扩展速率降低约12.0%。这进一步表明，在裂纹由浅向深扩展过程中，喷丸强化层都会对其扩展起到抑制作用。

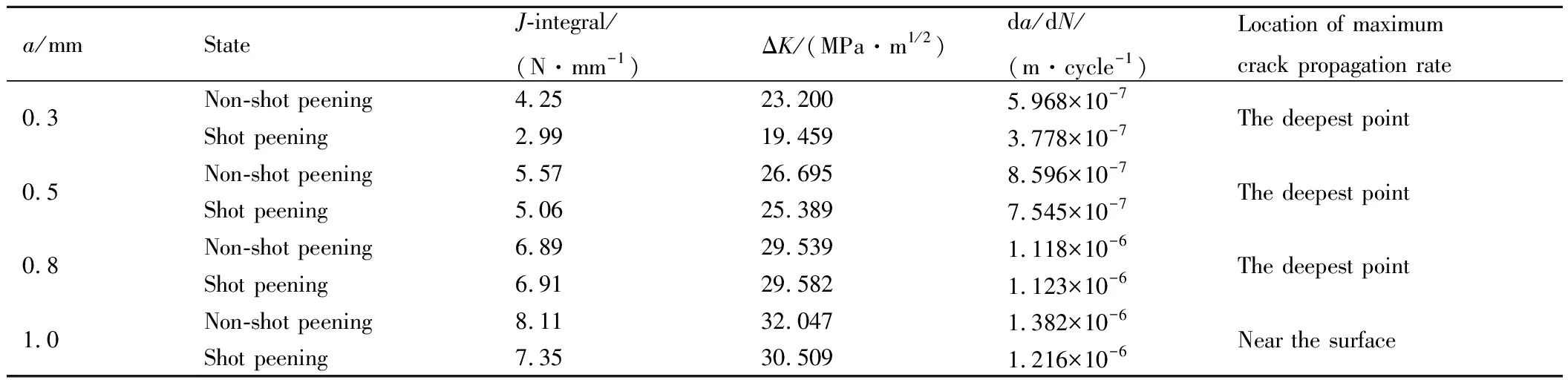
表1 喷丸件与未喷丸件的裂纹前沿最大裂纹扩展速率Table 1 Maximum crack propagation rate at crack front of shot peening and non-shot peening

3.4 丸粒速率对裂纹扩展的作用

3.4.1 丸粒速率对J积分值的影响

分别采用25，30，40m/s的初速度进行喷丸强化后，改变约束条件引入0.5mm深的裂纹并加远场拉伸载荷，由式(3)得到的裂纹前沿J积分值如图7所示。在丸粒速率较小的情况下，裂纹前沿的J积分值与未喷丸处理的J积分值差别较小，J积分值随丸粒速率的增大而降低，当丸粒初速度为40m/s时，裂纹前沿J积分值降幅约42.6%。表明较大的丸粒速率对抑制裂纹的扩展更有益。

图7 不同丸粒速率下的裂纹前沿J积分Fig.7 J-integral along the crack front with different shot velocities

3.4.2 丸粒速率对裂纹面张开位移的影响

提取加载后上下裂纹面对称线的节点坐标得到裂纹面轮廓曲线，如图8所示。由裂纹轮廓曲线可以直接计算和观察裂纹张开位移，丸粒速率为25m/s时，约0.22mm深范围内受到喷丸强化层的作用，裂纹张开位移降低。随丸粒速率的增大，约0.5mm深的范围内，裂纹张开位移显著下降，这从另一方面证明了喷丸强化对裂纹扩展的抑制作用。

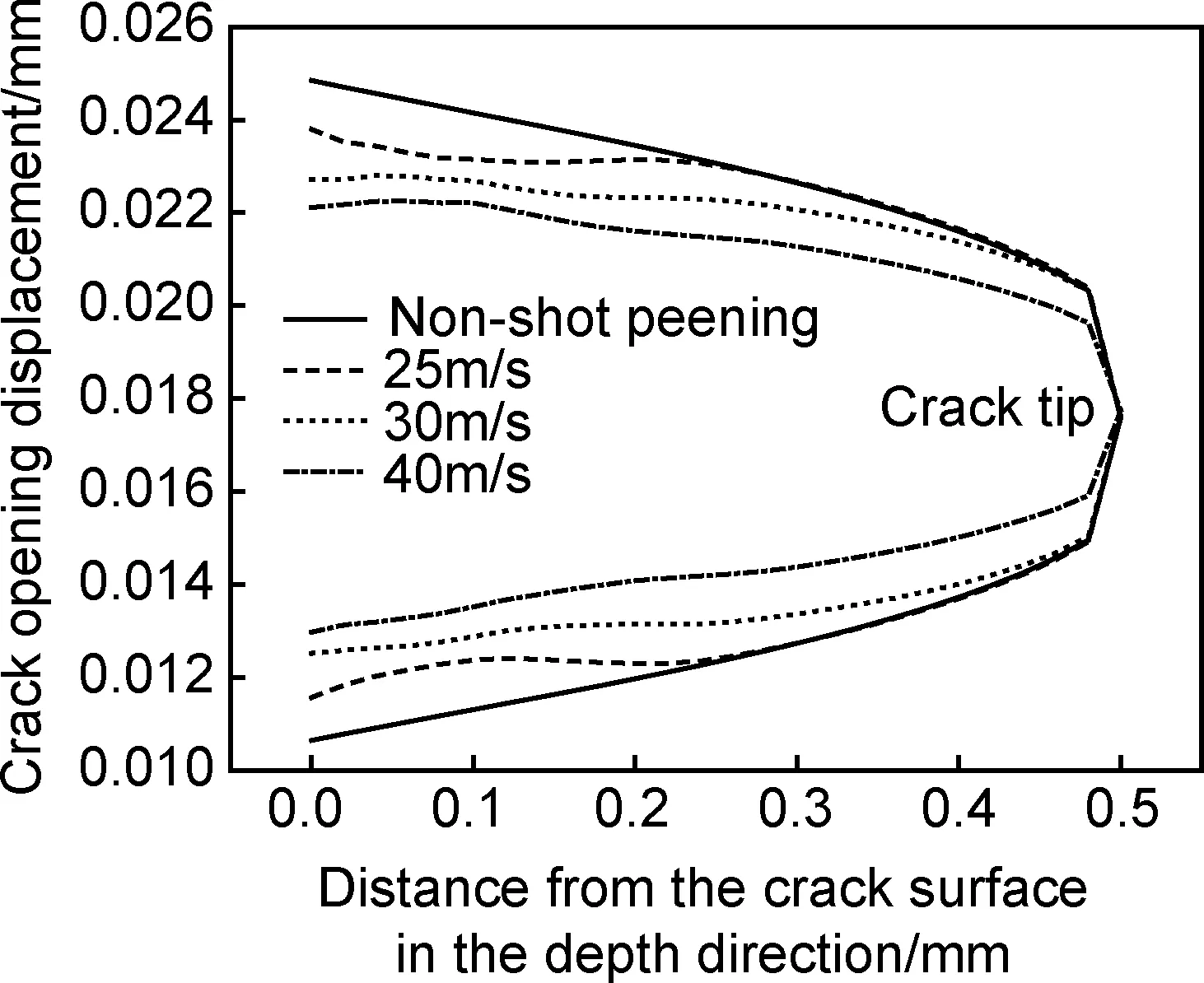
图8 不同丸粒速率强化后远场载荷下的裂纹张开轮廓Fig.8 Crack opening profile after strengthened by different shot velocities and under far field load

3.4.3 丸粒速率对裂纹扩展速率的影响

不同丸粒速率喷丸强化后，引入0.5mm深的裂纹并加载，裂纹最深点的最大扩展速率结果见表2。与未喷丸相比，在丸粒速率较小时(初速度为25m/s)，裂纹最深点的扩展速率差别很小。随丸粒速率的增大，给定载荷下的裂纹扩展速率明显降低，40m/s时降幅达45.1%。表明裂纹深度一定时，提高丸粒速率对抑制裂纹扩展更有益。

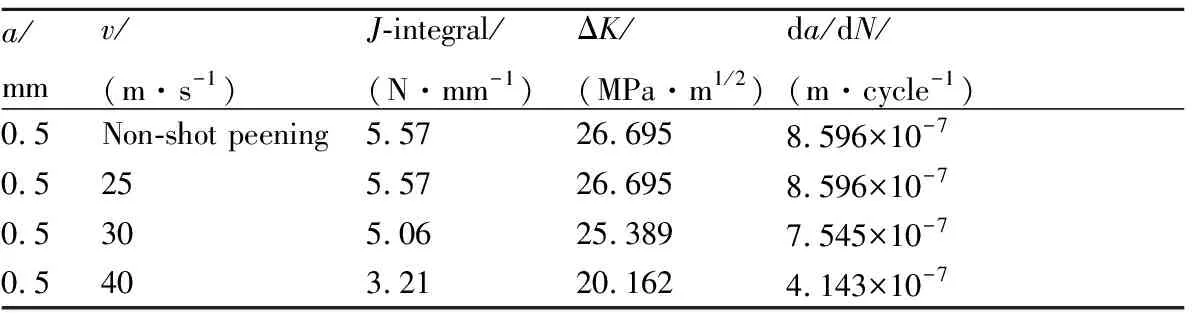
表2 不同丸粒速率下喷丸裂纹最深点的最大裂纹扩展速率Table 2 Maximum crack propagation rate at the deepest crack point with different shot velocities

4 结论

(1)采用修正的J积分计算得到的喷丸强化后裂纹前沿的J积分值的路径相关性很小，表明采用该公式计算的J积分值可以作为裂纹前沿断裂力学参数，用于评价喷丸强化件在远场应力作用下的裂纹前沿应力场强度。

(2)丸粒速率一定时，与未喷丸相比，喷丸后J积分值的降幅随裂纹深度的增加而减小，表明喷丸强化有益于抑制疲劳浅裂纹的扩展。当裂纹深度为0.3mm时，裂纹最深点的J积分值降幅约30.1%。

(3)裂纹较浅时，喷丸强化后裂纹前沿局部坐标系下的3个正应力分量降幅较大，且裂纹两端(靠近近表面)比裂纹最深点处的正应力分量的降幅小。降幅随着裂纹深度的增加而减小。

(4)裂纹深度一定，较大的丸粒速率更有益于抑制裂纹扩展，裂纹前沿J积分值、裂纹张开位移与裂纹扩展速率均有降低。丸粒速率为40m/s时，0.5mm深的半椭圆表面裂纹的最大J积分值降幅约42.6%，扩展速率降幅达45.1%。