基于小波变换域的数字图像嵌入和提取方法*

刘 琰，周 理

(1.福建工程学院 信息科学与工程学院，福州 350118；2.湖南城市学院 机械与电气工程学院，湖南 益阳 413000)

计算机技术、数字技术和互联网技术的进步使人们的生活发生了翻天覆地的变化.人们可以轻松地通过网络得到所需的各种视频、音频和图像等资源.这种变化在方便人们的工作和生活的同时，也带来了版权保护问题.版权保护一方面需要严格的法规制度，另一方面需要采用相应的技术措施.水印技术[1-2]作为一种有效的版权保护措施，近年来成为一个研究热点.水印技术是指通过特定的手段在图像或音频文件中嵌入带有特定标识的信息，需要时可以利用相应的手段将该信息提取出来的技术.目前，数字图像水印嵌入技术主要在空域和变换域两个方面进行.在空域中的水印嵌入技术比较容易实现，但是存在鲁棒性弱等缺点.在变换域中的水印嵌入技术是指先将数字图像进行特定变换，在变换结果中嵌入水印的方法.该技术虽然比较复杂，对计算资源要求较多，但是其隐身性和鲁棒性均较高，成为目前主流的水印嵌入技术.基于离散余弦变换的水印技术、基于压缩感知的水印技术、基于奇异值分解的水印技术等[3-7]，这些技术在一定程度上解决了水印技术中的隐身性、鲁棒性和安全性等问题，但是都不能全面地覆盖所有要求.本文在结合各种技术优点的基础上，提出了一种基于小波变换域[8]的数字图像水印嵌入和提取方法，将小波变换、Arnold置乱变换和奇异值分解有机结合，实现了具有较高安全性、隐身性和鲁棒性的数字图像水印的嵌入和提取功能.

1 算法模型

1.1 离散小波变换模型

(1)

式中：WTf(j，k)为离散小波变换系数；Ψj，k为离散小波函数.相应的逆变换为

(2)

式中，Q为离散小波基函数的上界.

小波变换用于图像处理就是利用小波变换将数字图像分解成不同频率和不同空间下的子图像，利用小波变换实现对数字图像多尺度的时频分解.利用一次小波变换可以将图像分成低频、垂直、水平和对角线四个频带.低频部分(LL)是图像在水平和垂直两个方向上经过低通滤波器后剩下的概貌子图，可以对其进行二次小波分解.垂直部分(LH)是垂直方向上高频细节，代表数字图像中垂直方向细节信息在水平方向上的概貌.水平部分(HL)是水平方向上高频细节，代表数字图像中水平方向细节信息在垂直方向上的概貌.对角线部分(HH)是数字图像经过高通滤波器后剩下的概貌子图.图像经过一次和两次小波变换的结果如图1所示.低频部分包含了图像的大部分能量，垂直、水平和对角线部分主要反映图像的边缘和纹理信息，数字水印主要嵌入到图像的低频部分.

图1 小波变换示意图Fig.1 Schematic wavelet transform

利用小波变换对数字图像水印进行处理需要选择合适的小波基函数.小波基函数是小波母函数经过伸缩或平移变换得到的.选择合适的小波基函数对于实现优秀的数字水印具有重要的意义.Haar小波函数具有严格正交、计算复杂度低、支撑长度短等特征，运用到数字图像水印中具有优秀的性能.Haar小波函数为

(3)

该小波函数是一种正交小波，满足条件

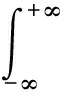
(4)

1.2 Arnold置乱变换模型

Arnold变换又叫猫脸变换.Arnold变换的重要特征是其具有周期性，图像变换一定次数后可以恢复到变换前图像的状态.由于嵌入了水印的数字图像在传输和保存等过程中可能出现损坏或信息丢失等情况，嵌入其中的水印图像也会发生损坏或信息丢失等情况.利用Arnold变换的周期性特征，通过对水印图像进行多次Arnold变换，可以将损坏的水印信息平均分配到整个水印图像中，减少损失信息对人眼视觉感受的影响.因此，数字水印中采用Arnold变换对水印图像进行预处理，可以提高水印算法的鲁棒性.Arnold变换公式为

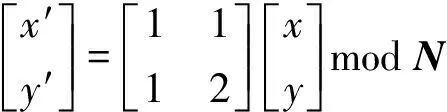
(5)

式中：(x，y)为变换前像素点的坐标；(x′，y′)为变换后像素点的坐标；N为图像的大小；mod为取模运算.利用P表示变换前的像素坐标向量，P′表示变换后的像素坐标向量，H表示变换矩阵，则单次Arnold变换可以表示为

P′=(H·P)modN

(6)

n次变换可以表示为

P(n)′=(Hn·P)modN

(7)

1.3 奇异值分解模型

奇异值分解是矩阵论中将矩阵对角化的方法.数字图像水印技术中应用奇异值分解主要是由于奇异值分解具有以下特点：一是图像的奇异值矩阵稳定性较高，不会因为对图像进行处理而剧烈变化；二是奇异值矩阵代表了图像的内在性质，改变矩阵的奇异值不会使人眼对图像的视觉感受产生较大变化.

将图像中的像素点用矩阵中的元素表示，像素点的灰度值为元素的值，则将图像表示成二维矩阵A，其大小表示为m×n.A的奇异值分解可以表示为

A=USVT

(8)

式中：U和V分别为m×n的正交矩阵；S为对角矩阵，其对角线上的元素满足

σ1≥σ2≥…≥σr≥σr+1=…=σm=0

(9)

其中，r为矩阵A的秩，σi为A的奇异值.A的奇异值分解是唯一的，每个奇异值是矩阵AAT的特征值平方根，而U的列向量和VT的行向量分别为AAT的特征向量.将U和V表示成向量形式，则奇异值分解可表示为

(10)

式中：ui为U的列向量；vi为V的列向量.

1.4 基于小波变换的水印嵌入和提取算法

小波变换具有与人类视觉系统相似的特征，将小波变换应用于数字水印具有其他方法无法代替的优势.本文提出了一种结合小波变换和奇异值分解的数字图像水印算法.该算法通过对待加入水印图像进行小波变换后再进行奇异值分解，将经过奇异值分解的水印图像加入到变换后的待加入水印图像中实现水印的嵌入过程，并通过逆变换实现水印的提取.

1.4.1 水印嵌入模型

对待加入水印的原始图像B进行两次离散小波变换，得到变换后的结果D，根据低频、垂直、水平和对角线四个频带将D分成七个部分，分别为LL2、HL2、LH2、HH2、HL1、LH1和HH1.

对水印图像S进行Arnold置乱变换得到置乱图像S1，变换的次数根据实际需要设定.将S1进行奇异值分解，得到奇异值矩阵SW，即

SVD(S1)=[UW，SW，VW]

(11)

选择原始图像B二次小波变换后的低频部分LL2作为嵌入水印的对象.对LL2进行奇异值分解，得到奇异值矩阵SLL2，即

SVD(LL2)=[ULL2，SLL2，VLL2]

(12)

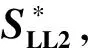
(13)

利用逆奇异值变换得到添加水印之后的低频部分LL2*，并对其进行两次小波逆变换得到嵌入水印的图像B*，表达式为

(14)

1.4.2 水印提取模型

(15)

(16)

2 实验及分析

2.1 水印效果及可见性分析

选择大小为256×256的Lena灰度图像作为需要嵌入水印的原始图像，水印图像为64×64的灰度二值图像，算法中Arnold变换的次数为10次，幅度调整比例α的值为50，选择Haar小波基函数.嵌入水印后的图像及水印提取结果如图2所示.

图2 实验结果Fig.2 Experimental results

由实验结果可知，嵌入了水印之后的图像和原始图像在视觉上基本没有任何差别，水印的嵌入没有对人眼的视觉感受产生影响.经过提取得到的水印图像与原始水印图像基本没有差别.因此，该算法能够很好地实现水印的嵌入和提取功能，并且提取出的水印图像准确度满足使用要求.实验中设置的Arnold变换次数为10次，变换的次数越多，对水印的置乱效果越好，某种程度上对水印的保护效果就越好，但是会明显地增加运算量，实际应用时需要根据实际情况灵活选择变换次数.实验中设置的幅度调整比例α的值为50，该值的大小会影响水印图像在原始图像中的可见度，需要根据使用要求决定.

为了定量表征水印的可见性，采用峰值功率信噪比(PSNR)作为该指标的度量.峰值功率信噪比定义为原始图像和嵌入水印后图像在各个像素点的灰度差值的函数，该值越大说明水印的效果越好，其表达式为

(17)

式中：X(i，j)和X′(i，j)分别为原始图像和嵌入水印后图像在位置(i，j)处像素的灰度值；I、J分别为图像的长度和宽度.在不同的α值时PSNR的结果如表1所示.

由表1可知，随着α值增大，PSNR减小，表示水印在结果图像中越来越可见.经验数据表明，PSNR大于30 dB时基本不会影响人眼对图像的观察.当α增大到100时，PSNR小于30 dB，从实验结果可以看出，结果图像较原始图像有细微变化，因此，需要根据实际情况灵活调整α值.

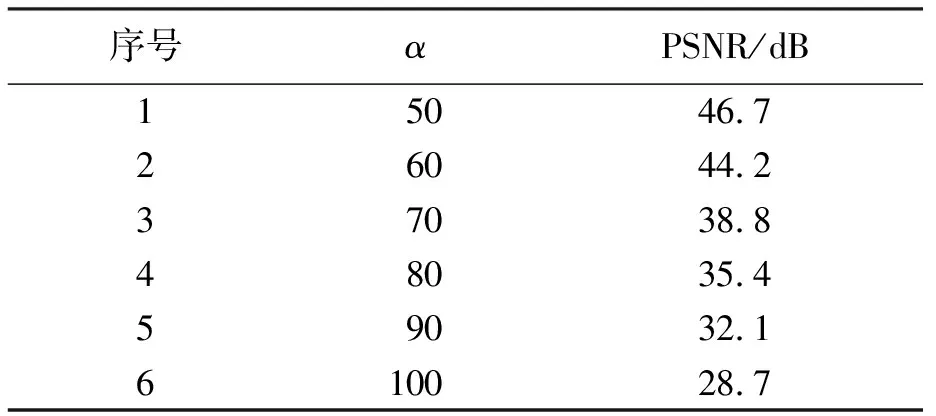
表1 PSNR数值表Tab.1 PSNR values

2.2 水印鲁棒性分析

水印的鲁棒性是指嵌入水印的图像受到各种噪声污染、压缩或裁剪等操作后，还能可靠提取出原始水印图像的能力.实验中采用归一化相关系数(NC)作为衡量水印鲁棒性的指标，其表达式为

(18)

式中：K和L分别为水印图像的长度和宽度；W′(i，j)和W(i，j)分别为提取的水印图像和原始水印图像在位置(i，j)处像素的灰度值.NC值越接近1，表示水印的质量越好，通常有效的水印算法中NC值必须大于0.5.

分别对在不同强度的椒盐噪声、高斯噪声和JPEG压缩、高斯平滑、裁剪操作等攻击方式下水印的NC值进行实验，每项NC值采用20次实验后取平均结果作为最终结果.实验数据如表2所示.

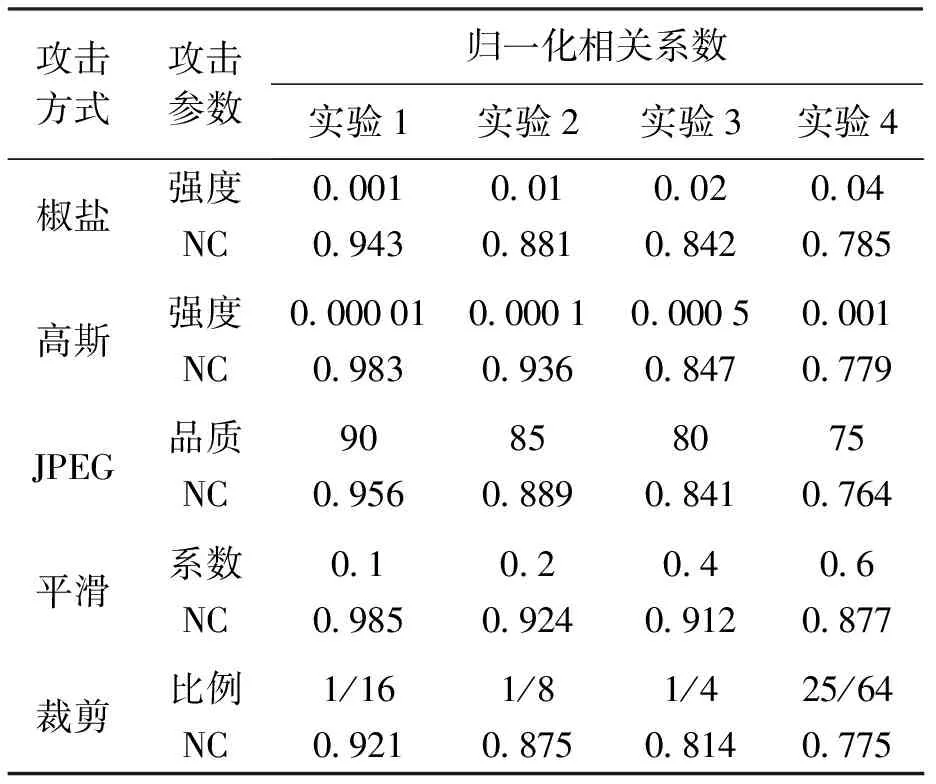
表2 鲁棒性实验结果Tab.2 Experimental results of robustness

由实验结果可知，在各种强度的椒盐噪声和高斯噪声的污染下，水印图像的NC系数均大于0.77，远高于0.5的标准，说明该算法具有较好的抗噪声干扰能力.在JPEG压缩、高斯平滑和裁剪操作等攻击方式下，水印图像的NC系数均大于0.76，同样远高于0.5的标准，说明该算法在各种常见攻击下均具有良好的效果.图3为表2中最后1列所示参数攻击下提取的水印图像.由图3可知，各种噪声污染和处理攻击下人眼均能较清晰地辨别出水印图像的内容，因此，该算法具有优秀的鲁棒性.

图3 各种操作后的水印提取结果Fig.3 Results of watermark extraction after various operations

3 结 论

本文提出了一种基于小波变换域的数字图像水印嵌入和提取方法.该方法将离散小波变换、奇异值分解和Arnold置乱变换有机地结合在一起，利用Arnold置乱变换对水印图像进行变换，增加水印算法的安全性，通过二次离散小波变换得到原始图像的低频部分，然后对原始图像的低频部分和置乱后的水印图像进行奇异值分解，分解结果通过加性准则实现水印的嵌入.实验结果表明，该算法能够有效地实现水印的嵌入和提取操作，嵌入水印后不会影响人眼对图像的观察.在椒盐噪声、高斯噪声、JPEG压缩、高斯平滑和裁剪操作等各种污染和攻击措施下，算法的NC值均大于0.7，人眼能够轻松地辨别出提取的水印图像，表明该算法具有较强的鲁棒性.