地震波传播方向对风力机动力响应的影响*

李德源，张世亮，池志强，张湘伟

(1.广东工业大学 a.机电工程学院，b.广东省创新方法与决策管理系统重点实验室，广州 510006；2.广东理工学院，广东 肇庆 526000)

为了更有效地利用风能，风力机风场多数建立在风能资源比较丰富的区域，其中也有些是地震活跃地带[1].运行中的风力机不仅受到空气动力载荷的作用，也可能面临突发地震的冲击[2].风力机结构属于质量较大而且高耸的结构，当风力机受到气动与地震等多种载荷同时作用时，风力机的结构安全和稳定运行都难以得到保证[3-4].研究表明，相对于竖向地震载荷，水平地震载荷是影响风力机可靠性运行的主要因素.由于地震波传播方向的不确定性，研究不同水平地震方向对风力机响应的影响对保证风电机组可靠运行具有重要意义.

1 地震动力学模型

1.1 土构耦合模型

根据土体性质和基础尺寸确定弹簧刚度和阻尼系数为

(1)

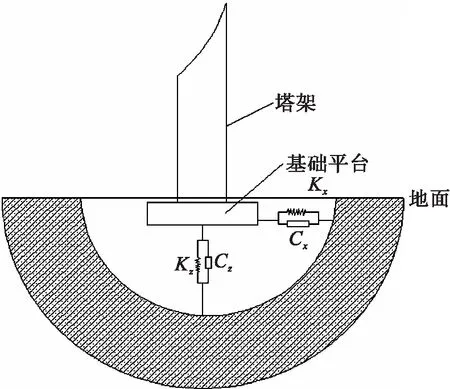
图1 土构耦合模型Fig.1 SSI model

(2)

式中：下标x、y、z为方向，x为来流风速的方向，z为垂直方向；Gs、μs和ρs分别为土壤的切变模量、泊松比和密度，本文根据实际情况取值分别为55 MPa、0.333和2 700 kg/m3；Rs为基础平台的半径[7].

1.2 地震加速度谱

抗震设计用的加速度反应谱在我国抗震设计规范中称为地震影响系数α曲线，地震影响系数最大值αmax决定于烈度，谱形状决定于场地相关反应谱.风电高塔系统属于高耸结构，水平方向和竖向地震载荷都不能忽略.本文依据国内抗震设计标准GB50011-2010模拟生成了水平和竖向两个方向的加速度时程，地震载荷以加速度时程的形式作用在基础平台.图2为地震水平方向地震影响系数曲线.

图2 地震影响系数曲线Fig.2 Seismic impact coefficient curve

地震水平向影响系数表达式为

(3)

式中：α(t)为地震影响系数；αmax为地震影响系数最大值；Tg为特征周期；T为结构自振周期，取1 s；y为衰减系数；η1为直线下降段斜率调整系数；η2为阻尼调整系数.当结构阻尼比不等于0.05时，曲线衰减系数y、η1和η2表达式为

y=0.9+(0.05-ζ)/(0.3+6ζ)

(4)

η1=0.02+(0.05-ζ)/(4+32ζ)

(5)

η2=1+(0.05-ζ)/(0.08+1.6ζ)

(6)

式中，ζ为阻尼比.按照当地实际情况选择合适的地震影响系数最大值和特征周期，对目标加速度反应谱进行模拟，可生成水平向地震加速度时程.本文仿真分析设置该风力机抗震烈度为9度，地震影响最大系数为0.4g(g为重力加速度)，特征周期为0.45 s，阻尼比为0.02，地震加速度发生时间为仿真的第10 s，总仿真时间为40 s，目标地震影响系数曲线和生成的水平向地震加速度时程如图3、4所示.

图3 目标地震影响系数曲线Fig.3 Target seismic impact coefficient curve

图4 地震加速度时程Fig.4 Seismic acceleration time-history

2 风力机地震风弹性耦合模型

2.1 风载荷

计算风力机叶片气动载荷的方法有很多，如叶素动量理论(BEM)、涡流理论、动态失速模型(BL)以及计算流体力学(CFD)等.其中叶素动量理论(是叶素和动量理论的耦合)在风力机气动载荷分析领域得到广泛应用和认可，本文也采用这种模型进行叶片气动载荷分析[10].

2.2 风力机多体动力学方程及数值求解

风力机由相对轮毂转动的风轮、轮毂、机舱、塔架和基础平台等组成，各部分间存在相对运动，且机组工作时，各部分的运动与变形各不相同.采用刚柔混合多体模型建立风力机动力学模型[11]，得到风力机多体模型后，可以根据多体动力学理论建立系统动力学方程，即

(7)

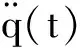
图5 动力学仿真流程图Fig.5 Flow chart of dynamics simulation

3 仿真算例

以美国可再生能源实验室(NREL)开发的5 MW变速变桨距控制风力机组为对象进行分析，该机组性能参数可参阅文献[10].利用超级单元的离散方法，将叶片离散成4个超级单元，一共13个刚体.因为主轴会产生扭转，故将其分成两个刚体，用旋转铰连接.由于轮毂与主轴第一个刚体连接且无相对位移，可以当成一个刚体，机舱也作为一个刚体，机舱与塔架用球铰连接，塔架第一个刚体和基础平台刚性连接，整个风力机被分成55个刚体，91个自由度，建立的整机混合多体模型如图6所示.在额定风速11.4 m/s的工况下，对风力机分别输入两个水平地震方向(平行于来流方向的正向和垂直于来流方向的侧向)，根据风力机的动力学响应结果分析不同水平地震方向对风力机振动变形的差异.

图6 整机坐标示意图Fig.6 Schematic coordinate of whole machine

3.1 机舱加速度时域响应

机舱加速度变化是反应塔尖振动情况的特征响应之一，图7、8分别为机舱两个水平方向加速度(即x、y方向)随时间的变化曲线.从机舱两个水平方向的加速度变化图可以看出，正向地震主要影响机舱x方向的加速度，而侧向地震主要影响机舱y方向的加速度，响应结果和地震方向一致.

3.2 叶片振动变形加速度时域响应

叶片叶尖处是振动变形最明显的位置，图9为第三个叶片叶尖处挥舞方向振动变形加速度随时间变化曲线，图10为第三个叶片叶尖处摆振方向振动变形加速度随时间变化曲线.

由叶尖振动变形加速度随时间的变化图可以看出，正向地震主要影响叶片挥舞方向的振动变形，且和模拟生成的地震加速度时程趋势一致.侧向地震对叶片两个方向的振动变形都有明显影响，相比于正向地震，衰减速度要慢很多.在叶片挥舞方向上，正向地震要比侧向地震影响程度大，最大加速度在第13.8 s达到了19.29 m/s2，比在没有受到地震作用下大12 m/s2，但在30 s后侧向地震明显要比正向地震影响显著.在叶片摆振方向上，侧向地震比正向地震的影响更大.

图7 机舱x方向加速度随时间的变化图Fig.7 Change of acceleration with time in x direction of cabin

图9 叶尖挥舞方向振动变形加速度Fig.9 Flapwise vibration deformation acceleration of blade tip

图10 叶尖摆振方向振动变形加速度Fig.10 Edgewise vibration deformation acceleration of blade tip

3.3 载荷分析

叶片在叶根处承受着较大的挥舞力矩和摆振力矩，是风力机叶片结构设计的关键点，故叶根力矩在地震作用下产生的变化对叶片抗震设计具有重要参考价值.由于地震作用在基底，塔基受到的俯仰和横摇力矩也会随之发生变化.

叶根挥舞与摆振力矩随时间的响应曲线如图11、12所示，由图11、12可以看出，风力机受到正向地震时，叶根挥舞力矩在6.7～8.1 MN·m之间变化，最大值比没有受到地震作用时要大1.1×105N·m；相对于叶根挥舞力矩，叶根摆振力矩在正向地震时没有明显变化.当风力机受到侧向地震时，叶根挥舞力矩和摆振力矩都有明显波动，但叶根挥舞力矩变化要比摆振方向力矩变化明显.叶根摆振力矩在-5.5～2 MN·m之间波动，最大值比没有受到地震作用时要大8×105N·m.依据叶根挥舞力矩和叶根摆振力矩的响应曲线可以看出，正向地震对叶根挥舞力矩影响尤为明显，侧向地震则主要影响摆振方向叶根处力矩.

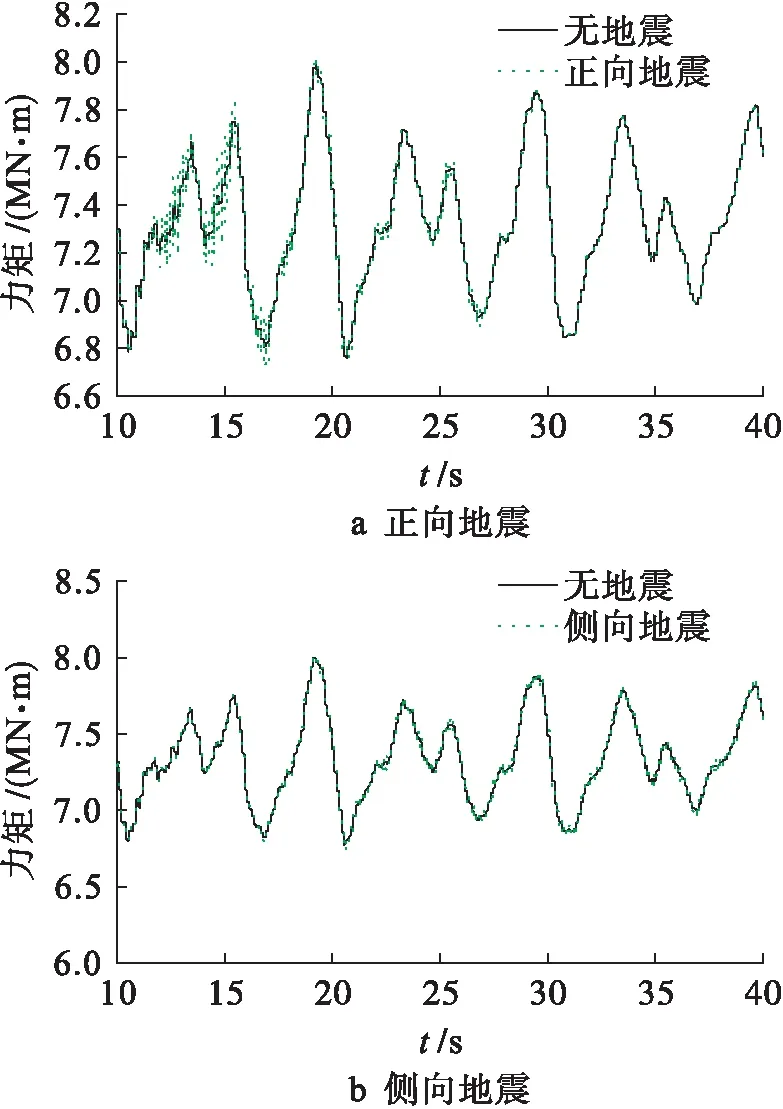
图11 叶根挥舞力矩Fig.11 Flapwise moments of blade root

塔基的俯仰力矩和横摇力矩如图13、14所示，由图13、14可以看出，风力机受到正向地震作用时塔基的俯仰力矩变化比横摇力矩的要明显，此时塔基的俯仰力矩在-5×107～1.7×108N·m之间波动，力矩最大值比在没有受到地震作用时大7×107N·m.相反，风力机受到侧向地震作用时塔基的横摇力矩变化比俯仰力矩的要明显，此时塔基的横摇力矩在-2.2×107～2.2×107N·m之间变化，力矩最大值比在没有受到地震作用时大1.1×107N·m.从塔基的力矩响应可以看出，正向地震主要影响塔基的俯仰力矩，侧向地震主要影响塔基的横摇力矩.

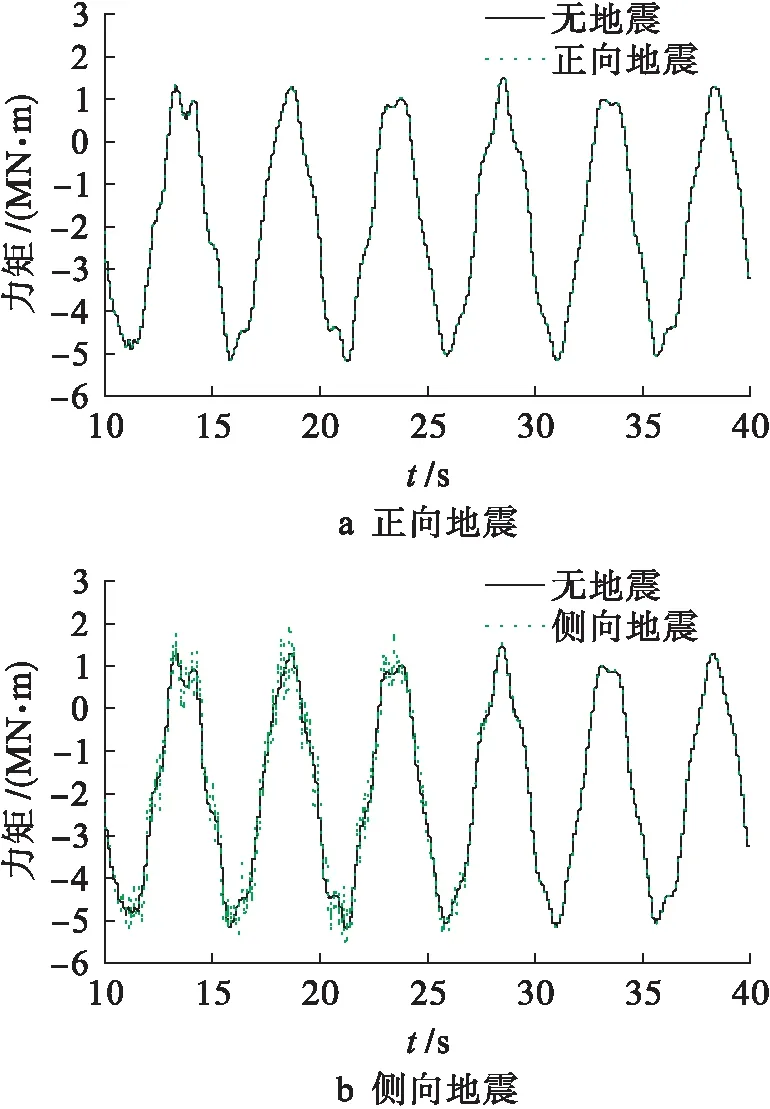
图12 叶根摆振力矩Fig.12 Edgewise moments of blade root

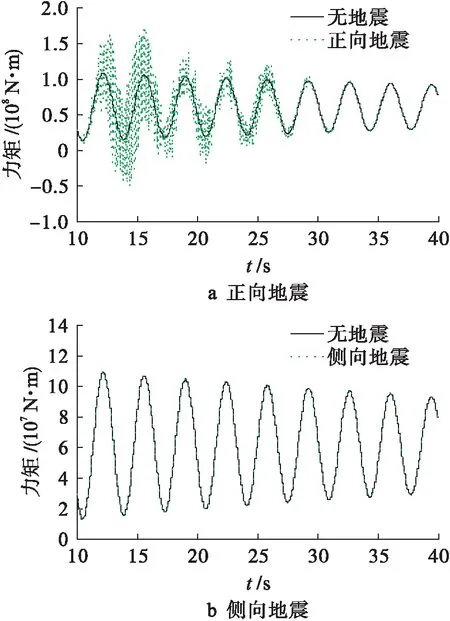
图13 塔基俯仰力矩Fig.13 Pitching moment of tower foundation

4 结 论

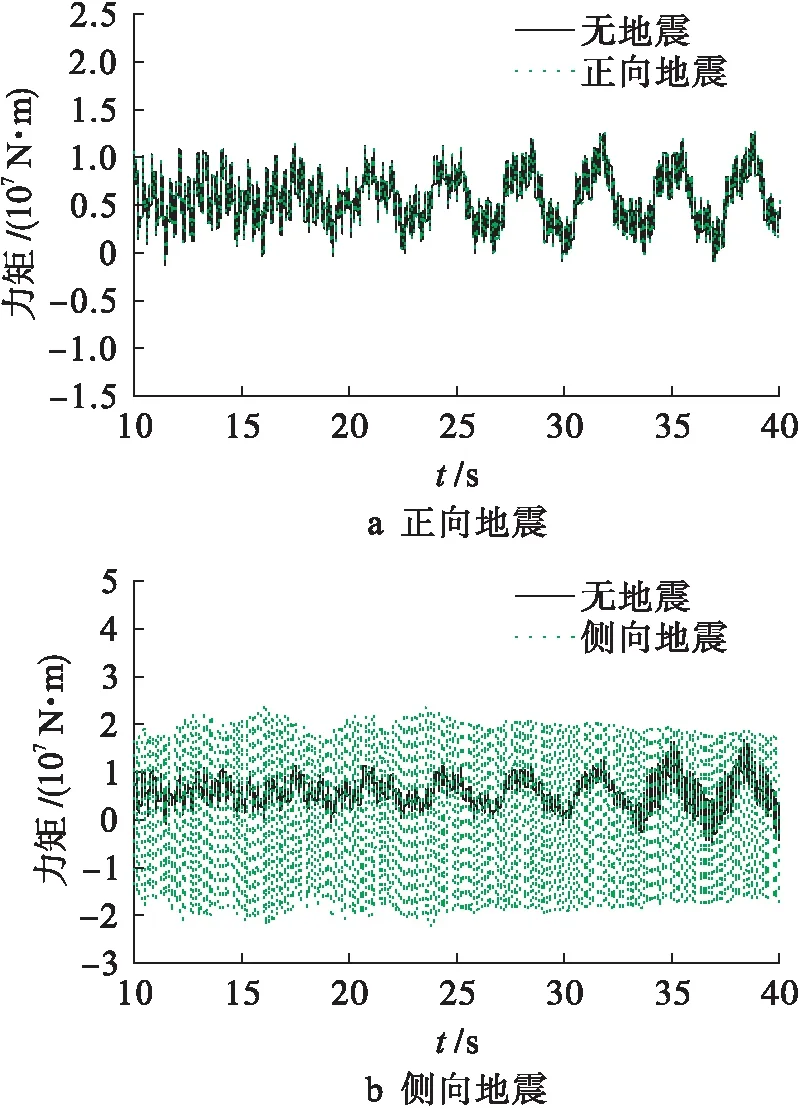
图14 塔基横摇力矩Fig.14 Rolling moment of tower foundation

1) 正向地震主要影响叶尖挥舞方向振动变形，其影响程度比侧向地震要更剧烈，侧向地震对叶片挥舞方向和摆振方向的振动变形都有影响，摆振方向上，侧向地震影响更明显.在叶根力矩方面，正向地震主要影响叶根挥舞力矩，最大值比原来增加了50.34%，侧向地震主要影响叶根摆振力矩，最大值比原来增加了66.67%.

2) 在地震作用下机舱的水平方向加速度和塔基的力矩都发生了明显变化，机舱的两个水平方向加速度响应和地震方向保持一致，正向地震主要影响塔基的俯仰力矩，最大值比原来增加了63.62%，侧向地震主要影响塔基的横摇力矩，最大值比原来增加了98.23%.

3) 研究工作对于风力机组的抗震设计与保障机组的安全稳定运行，特别是考虑地震波不同的传播方向对运行中机组的冲击具有参考价值.