异形钢结构建筑铸钢节点空间加载试验与有限元分析

□文/高树才 吴伸杰 马 旭 荣 彬

铸钢节点具有受力明确、传力直接、承载力大的特点，通常节点体型大、受力复杂，多用于结构体系的关键节点，其可靠性直接影响结构的安全，而目前的理论分析和设计方法尚不成熟，仅依靠数值模拟的结果进行设计显得不够安全，因此国内外的重点工程都对不同形式的铸钢节点的受力性能开展研究。丁阳等[1]为考察天津奥林匹克中心体育场大跨度钢管桁架结构铸钢节点的受力性能，评价其安全性，对铸钢节点进行了足尺试验验和有限元分析，结合试验结果和有限元计算结果，分析了节点的应力分布规律，表明天津奥林匹克中心体育场铸钢节点具有较高的承载性能和足够的安全性。徐世杰等[2]通过试验研究了重庆江北机场T3A航站典型铸钢节点的荷载-位移曲线，应力和节点破坏时的变形特征，使用有限元软件进行验证，对此类异形铸钢节点的使用和施工过程提出了优化建议。杜新喜等[3]对新疆国际会展中心屋面张弦桁架支座铸钢节点进行了1/2缩尺加载试验，试验结果表明在最不利设计工况组合下，节点满足设计的承载力要求；对节点试件进行了弹塑性有限元分析，有限元分析和试验结果吻合良好，在有限元数值模型可靠的基础上，对铸钢节点的承载性能指标和安全储备进行了综合评估。上述工程实例表明了铸钢节点具有良好的适用性，由于国内还没有一套成熟的铸钢节点设计方法，目前工程中的铸钢节点多采用有限元理论分析与试验测试结果相结合的方式来保证节点的承载安全性。

1 工程概况

中部国际设计中心建筑方案是著名国际建筑设计大师扎哈·哈迪德的遗作，裙房底盘平面形状呈不规则五角星形，形似花瓣。上部三角布置3栋塔楼，整体协调，浑然一体，见图1。

图1 中部国际设计中心

塔楼的形态以“花”为设计意向，外轮廓底部呈现弧线形的花萼形态，塔身赋以白色线条表示花的经络，轻盈曼妙。塔楼平面呈纺锤形的六边形。裙房外墙为直线曲线结合的横向玻璃带窗和铝板幕墙组合，形成流畅的建筑外立面。塔楼的塔基从下到上逐渐扩大到裙房屋面之上后慢慢内收，塔楼以玻璃幕墙和竖向装饰线条形成花瓣的肌理。

结构的难点在于塔楼3层以下外排钢管柱向核心筒逐步回收至内排柱，在一层交汇，部分节点由三斜管交汇，交汇位置受力复杂。若采用相贯焊接将导致焊接应力过大，很难判断节点是否达到承载要求，故采用了铸钢节点。

2 节点概况

工程使用的铸钢节点的节点形式见图2。

图2 节点模型

主管竖直连接下层柱子，主管的前部与三根斜管相贯，后部支撑3根水平梁。节点为1/2缩尺模型，主管外径为450 mm、壁厚45 mm，各支管外径400 mm、壁厚40mm，主管后三个水平梁截面尺寸340 mm×165 mm×35 mm，各管交汇区域上部倒角尺寸为30 mm，下部的倒角尺寸为200mm。

3 铸钢节点试验

3.1 加载工况

铸钢节点试验在天津大学结构试验室进行，加载采用设计组合工况，对于各管而言，设计荷载的轴力起控制作用，因此选择主管，支管B、C的最大轴力工况进行空间加载试验。见表1。

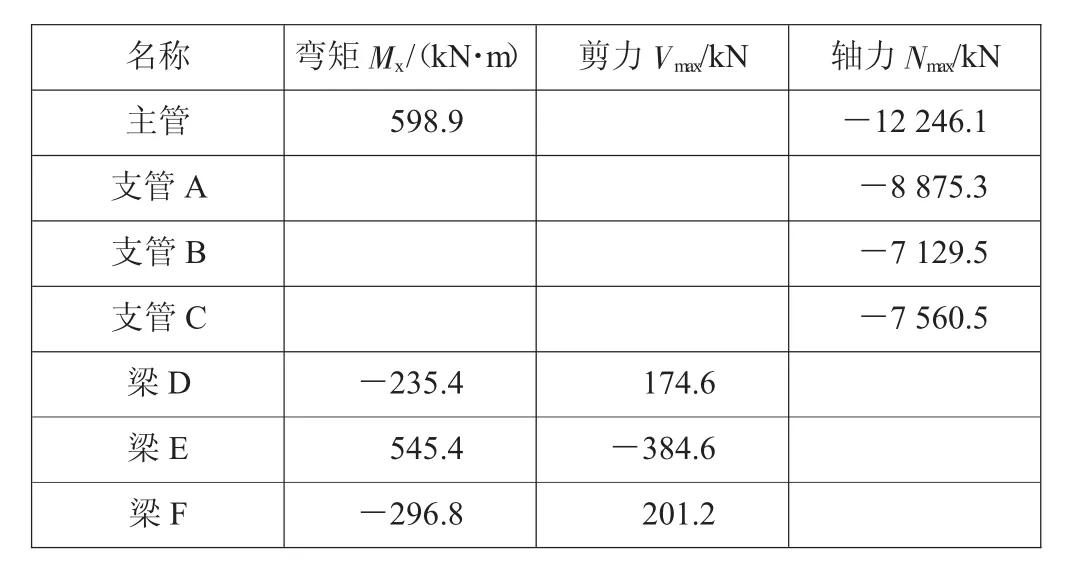
表1 试验荷载

表1中弯矩以梁的下部受拉为正，反之为负；剪力以使研究杆段转向为顺时针时为正，反之为负；轴力以受拉为正，受压为负。试验中加载的荷载为缩尺模型按照应力等效原则对应的换算值。

3.2 材性试验

铸钢材料选用G20Mn5QT，采用和节点同炉浇筑的方法进行试棒加工，见图3。

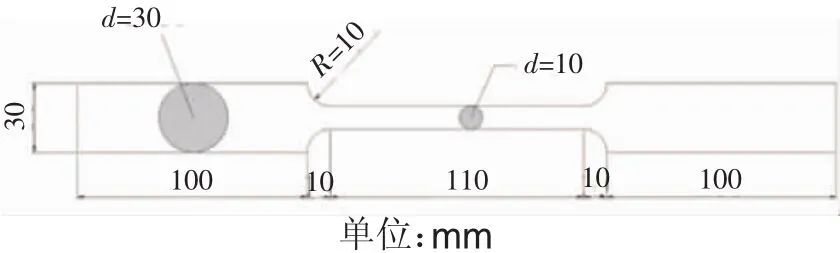
图3 材性试验试棒尺寸

3.3 试验装置

空间试验载装置见图4。

图4 试验装置

主管的竖向轴力由320 t单向千斤顶施加，加载分级通过油压表控制；水平剪力通过50 t单向千斤顶来施加，加载分级通过力传感器控制；各支管的轴力由3个200 t单向的千斤顶施加，通过设计的支座传力至反力墙，加载分级通过油压表控制。

主管竖向力通过上端横梁传递给两侧的加载反力架。加载支管的斜向千斤顶连接加载支座并支承于反力墙上。主管底部焊接底板并在底板上设置支座，以焊接连接水平梁，整个节点采用锚栓固结在地面。

3.4 加载制度

试验加载分为预加载和正式加载，预加载阶段施加设计荷载的30%，分三级加载，然后卸载，为正式加载做准备。预加载结束后，进行正式加载。为保证各管加载的同步性，荷载分10级加载，加载到每级荷载后持荷，采集应变数据后进行下一级加载。

3.5 测点布置

铸钢节点应变测点布置见图5。在有限元分析的基础上，将测点布置在节点应力集中的节点倒角部位。1号节点试件共布置应变花22个，应变片22个；2号节点试件增加柱底水平梁一侧5个应变花。

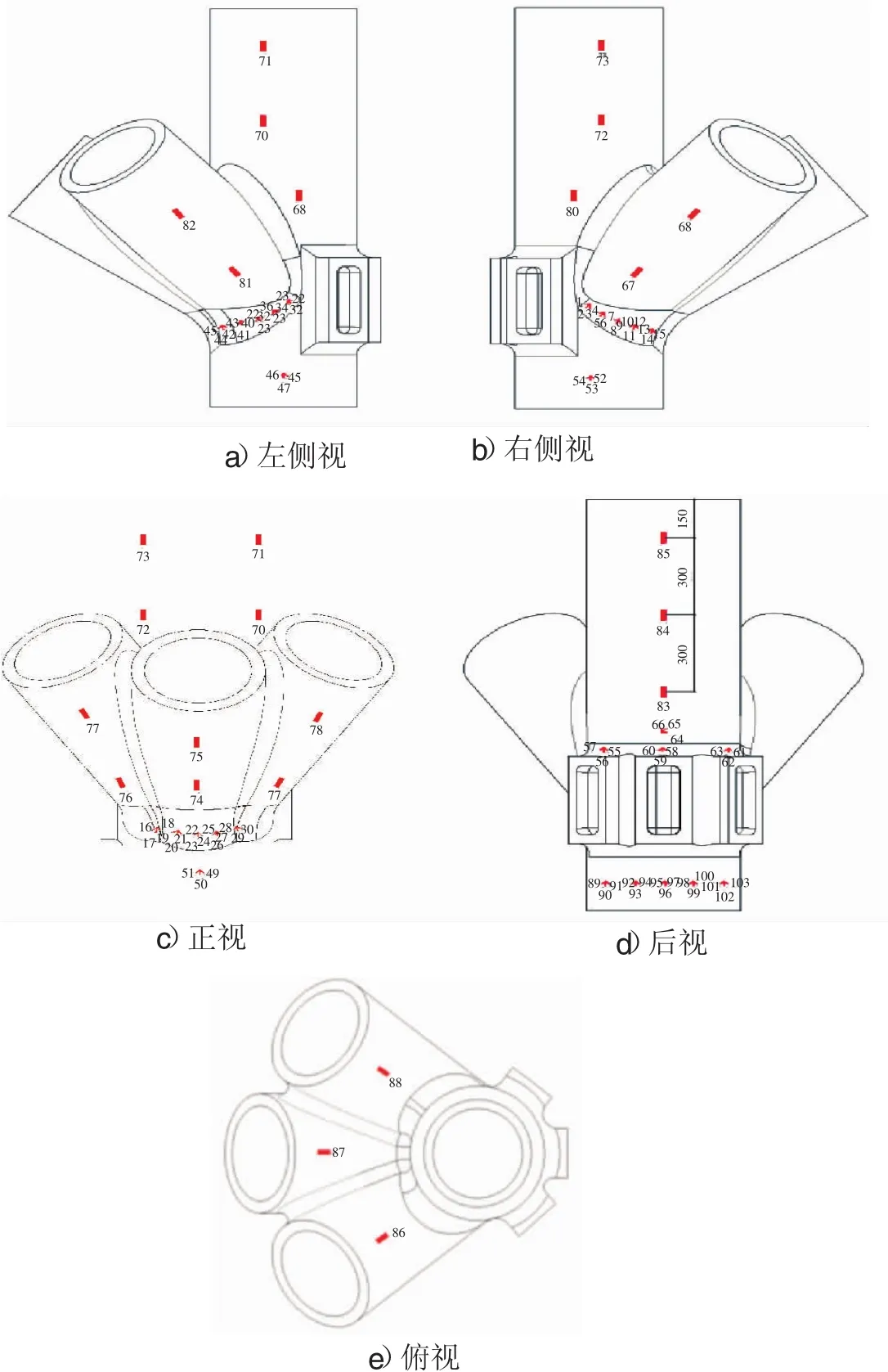
图5 试验测点布置

3.6 试验结果分析

为方便表述，使用应变花中编号最小的应变片，来指代这个应变花（例如应变片花1号为应变片1,2,3组成的应变花）。试验结果统计中，将应变花和应变片的测量结果换算为测量位置的等效应力。见图6和图7。

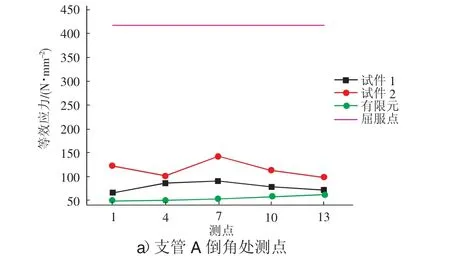
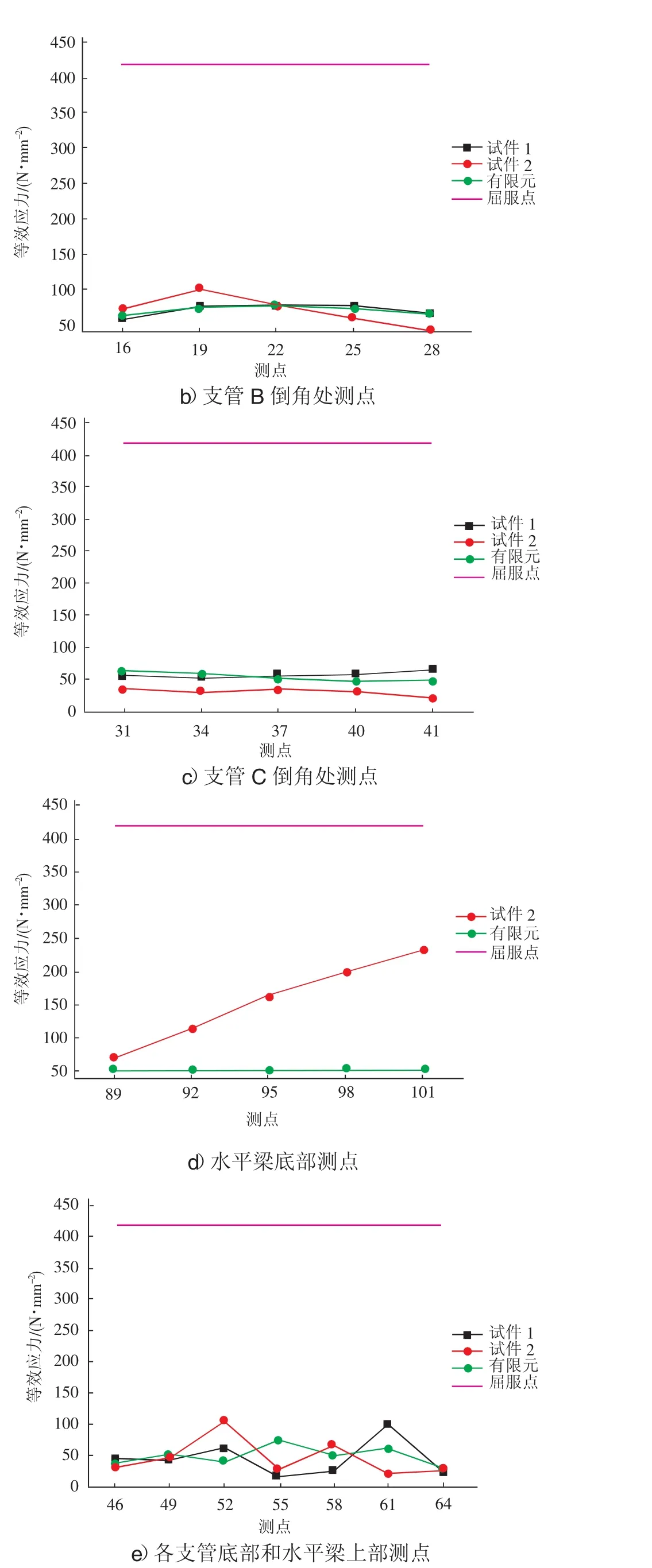
图6 应变花等效应力

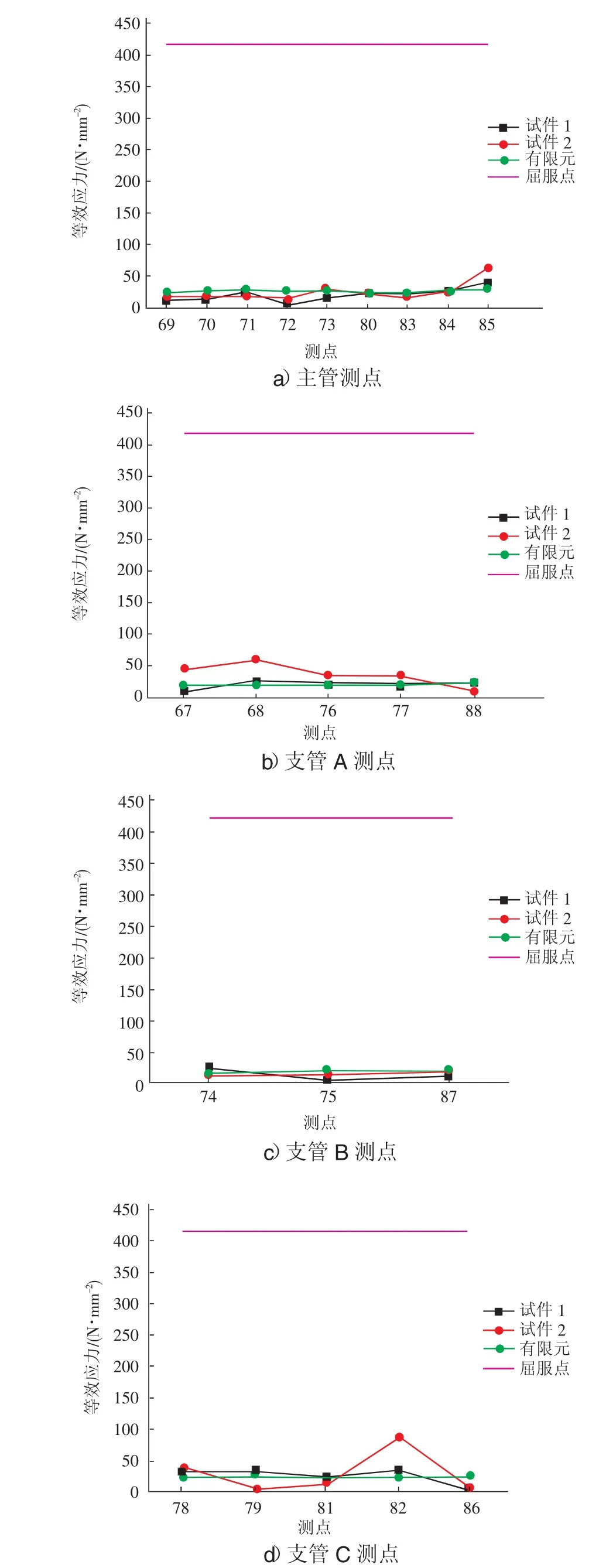
图7 应变片等效应力

1号节点的最大等效应力为98.74 N/mm2，出现在61号应变花，位于水平梁F上侧。A支管倒角处的应变花为1～13号，最大等效应力为89.93 N/mm2。B支管倒角处的应变花为16～28号，最大等效应力为73.44 N/mm2，C支管倒角处的应变花为31～43号，最大等效应力为62.01 N/mm2。应变花46、49、52号为测量主管柱底部的应力水平，较支管倒角部分，此处的等效应力相对较小。应变花55、58、61号测量的是水平梁上侧等效应力大小，最大等效应力为98.74 N/mm2。水平梁上部的应变花64号的应力较小。

2号节点的最大等效应力为233.47 N/mm2，出现在101号应变花，位于水平梁F的下部靠近柱底。A支管倒角处的应变花为1～13号，最大等效应力为142.60 N/mm2。B支管倒角处的应变花为16～28号，最大等效应力为98.18 N/mm2，C支管倒角处的应变花为31～43号，最大的应力为 32.06 N/mm2。应变花 46、49、52号为测量主管柱底部的应力水平，较支管倒角部分，此处的等效应力相对较小。应变花55、58、61号测量的是水平梁上侧的等效应力，最大值为65.06 N/mm2。水平梁上部的应变花64号的应力较小。应变花89、92、95、98、101号测量的是柱底水平梁一侧的等效应力，最大值为233.47 N/mm2。

应变片主要测量的为主管，支管管壁的应力大小，除2号试件支管A管壁82、85号测点等效应力较大，其他测点应力较小。在试验荷载下，节点在各支管底部倒角处和节点底部的应力水平相对较高，起到控制作用，管壁的应力相对较小。

4 有限元分析

4.1 有限元模型

有限元分析中，节点模型采用solid187单元模拟，solid187单元是10节点四面体单元，具有塑性、大变形和大应变特点，适用于模型的复杂网格划分。铸钢的材料屈服强度417.63 N/mm2，抗拉强度554.29 N/mm2，弹性模量为2.13×105 N/mm2，泊松比0.3。有限元分析中铸钢材料采用理想三折线随动强化应力应变模型，见图8。

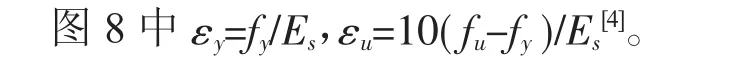
有限元分析中，采用Von Mises屈服准则，显示对比结果的Von Mises应力。为保证分析结果的准确性，网格尺寸选择为节点管壁厚的1/2[5]，节点的网格划分见图9。为准确模拟试验中节点的受力状态，约束了节点底部和水平梁端的全部位移和转动。

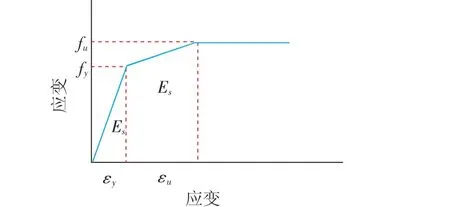
图8 有限元分析中铸钢材料的本构模型

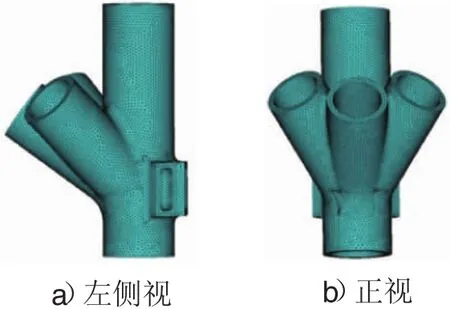
图9 铸钢节点的网格划分

4.2 有限元结果和试验结果对比

有限元分析的结果见图10，试验荷载下有限元分析结果和试验结果对应测点的应力大小对比见图6和图7，有限元分析结果与试验结果整体较接近，证明有限元分析的可行性。

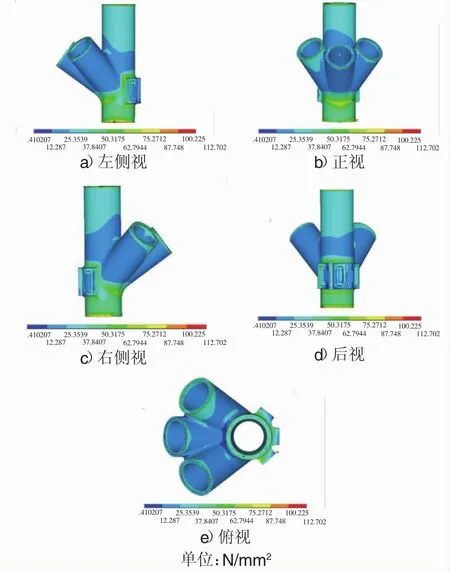
图10 有限元分析结果

对于有限元的结果，最大的等效应力出现在节点底部约束处，其次应力较大的部位仍是各支管下部的倒角部分，其中B支管下部倒角部位的等效应力更大。

5 结论

铸钢节点试验中，全部试验节点的最大应力均不超过屈服强度。对于1号节点试件，应力量测结果与有限元结果吻合较好，验证了有限元分析的可行性。对于2号节点试件，A支管和C支管应力出现明显的不对称性，节点受力不均匀，与节点实际受力情况不符，表明节点制作和安装误差对节点受力有较大影响，施工中应注意节点制作和安装精度。

试验结果表明，在最大设计荷载工况下，节点最大的等效应力为233.47 N/mm2，有限元结果表明，最大的等效应力为51.24 N/mm2，均小于材料屈服强度417.63 N/mm2。试验和有限元分析表明,节点的主管、支管底部和水平梁下部倒角处应力水平较高，施工时应注意这些位置处的应力监测。