基于非线性频偏的频控阵点状波束形成
冯晓宇,谢军伟,张 晶,王 博
(1.空军工程大学防空反导学院,陕西 西安 710051;2.陕西交通职业技术学院,陕西 西安 710018)
0 引言
基于相控阵的波束形成技术被广泛应用于雷达领域[1],相控阵能够在目标方向形成高增益,因而被广泛应用于雷达目标探测及干扰抑制[2]。但是相控阵雷达无法识别同一角度不同距离的两个目标,即相控阵波束仅具有角度分辨力,不具有距离分辨力,导致其不能抑制距离维的干扰。
2006年,P. Antonik在国际雷达会议上首次提出了频控阵雷达概念[3-4],并引起国内外学者的广泛关注。区别于相控阵,频控阵通过在阵元间加入一个远小于载频的频率增量,使天线波束的空间分布距离-角度二维相关[5],给雷达带来了更大的应用潜力。目前国内外已有很多文献对频控阵进行研究,文献[6-7]指出频控阵的波束扫描特性与阵元间频偏相关,文献[8-10]对频控阵的研究现状做了总结,分析了频控阵的结构及波束特性,对其应用进行了展望。文献[11]指出频控阵波束分布与距离、角度、时间相关,当固定其中一个变量,波束分布在另外两个变量上分布存在多极值。文献[12]通过引入时变频偏,在目标距离上形成了稳态波束。文献[13]引入log函数非线性频偏,使波束在空间形成唯一极值,但是主瓣的聚焦性不好,旁瓣较高。本文针对频控阵分布在距离-角度维存在多个极值的问题,提出了基于非线性频偏的频控阵点状波束形成方法。
1 FDA信号模型
均匀线阵FDA结构如图1所示。
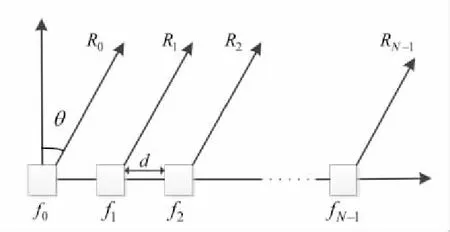
图1 均匀线阵FDA阵列Fig.1 Uniform linear array FDA
窄带条件下,各阵元发射信号可表示为:
sn(t)=exp(j2πfnt),n=0,1,…,N-1
(1)
式(1)中,fn=f0+nΔf,n=0,1,…,N-1;f0,Δf,N分别表示载频,频偏和阵元总数。
设空间中的某个目标位置为{R,θ},阵元n发射的信号到达目标的信号可表示为:
(2)
式(2)中,Rn=R-ndsinθ,d为阵元间距,c为光速。ULA-FDA在(R,θ)处产生的远场阵列因子为:
(3)
式(3)中,
而要让式(3)取得极值,需满足
(4)
当时间t固定时,由于频偏和阵元间距的同步线性变化,频控阵的方向图将出现角度与距离之间的耦合,而要消除这种耦合可采取两种方式,一种是采用线性增长频率增量和不均匀分布的线阵,另一种是采用非线性增长的频率增量和均匀线阵。本文采用第二种方式消除频控阵方向图距离角度耦合。
令f0=3 GHz,Δf=2 KHz,N=10,d=0.5c/f0,R=100 km,θ=20°时,ULA-FDA阵列的发射方向图如图2所示。
ULA-相控阵的发射方向图如图3所示。由图2、图3易看出FDA波束距离-角度二维相关,而相控阵波束仅具有角度分辨力。但是频控阵在距离-角度维上存在耦合。
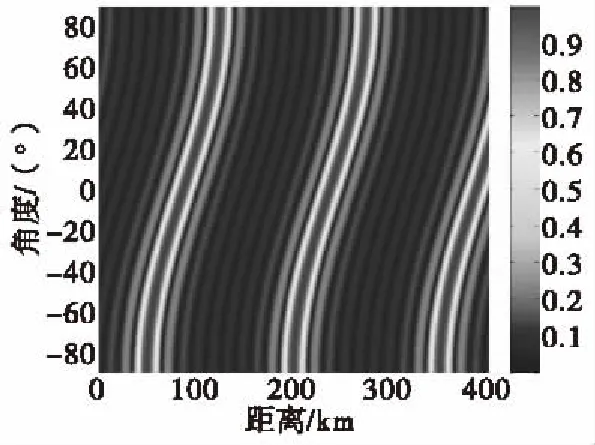
图2 ULA-FDA发射方向图Fig.2 The transmit pattern of ULA-FDA

图3 ULA-相控阵发射方向图Fig.3 The transmit pattern of ULA-PAR
图4是两种阵列在不同信噪比(SNR)下的输出信干噪比(SINR)对比图。从图中可以看出,在相同信噪比条件下,频控阵的输出信干噪比较大,即在相同的环境中,频控阵比相控阵具有更好的稳健性。
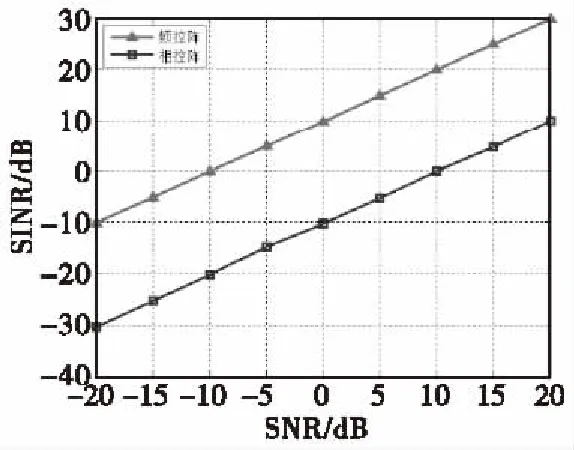
图4 SINR随SNR的变化图Fig.4 The change diagram of SINR with SNR
2 非线性频偏线阵FDA
针对基本FDA存在距离-角度耦合的现象,本文分别引入log函数分布、sin函数分布、平方分布、指数分布、倒数分布的非线性频偏,在目标位置形成点状波束,减弱或消除耦合现象。
2.1 log-FDA信号模型
引入呈log函数分布的非线性频偏[13],即
fn=f0+log(n+1)Δf,n=0,1,…,N-1
(5)
此时阵列因子可表示为:
(6)
wm为权矢量,当目标位置为(R′,θ′)时,方向图可被表示为:
(7)
2.2 sin-FDA信号模型
引入呈sin函数分布的非线性频偏,即:
fn=f0+Δfsinn,n=0,1,…,N-1
(8)
同理,推导出波束方向图为:
(9)
2.3 square-FDA信号模型
引入呈平方分布的非线性频偏,即:
fn=f0+Δfn2,n=0,1,…,N-1
(10)
波束方向图为:
(11)
2.4 倒数-FDA信号模型
引入呈倒数分布的非线性频偏,即:
(12)
当n=0时,令fn=f0,则波束方向图可表示为:
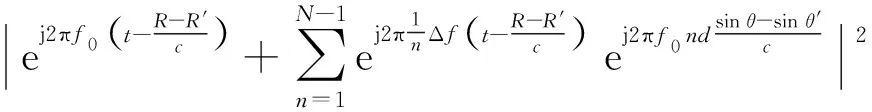
(13)
3 多频均匀线阵FDA
当引入非线性频偏时,波束的旁瓣增益较高,本文考虑单阵元发射多频信号的方法,改善波束形状。
3.1 基本ULA-FDA信号模型
在基本线阵FDA中,阵元发射同一的全向单频信号,考虑在单个阵元上发射一个多频信号。则阵元n第m个频率成分的载频表示为[14]:
fnm=f0+Δfn+Δfm
(14)
式(14)中,Δfn=nΔf,n=0,1,…,N-1表示阵列阵元间的频偏增量,N表示阵元数;M表示阵元发射的频率个数,Δfm=mΔf,m=0,1,…,M-1表示阵元发射不同频率成分时信号的频偏增量。
第n个阵元的第m频率成分的传输信号为:
(15)
远场观测点总的接收信号可以表示为:
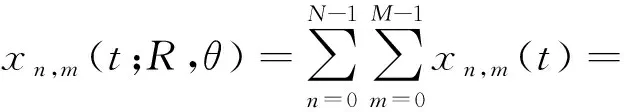
(16)
式(15)、式(16)中,wnm为各个阵元对应频率的发射权重,c为光速,(R,θ)为目标远场观测点。则多载波ULA-FDA的波束图表达式为:
(17)
3.2 log-FDA信号模型
在log-FDA非线性频偏信号的基础上,单个阵元发射多频信号,则Δfn=log(n+1)Δf,n=0,1,…,N-1,Δfm=log(m+1)Δf,m=0,1,…,M-1,其波束方向图可表示为:
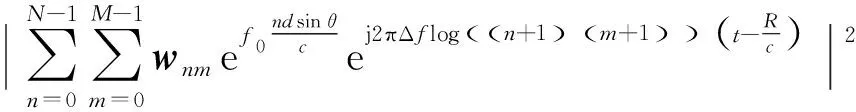
(18)
3.3 sin-FDA信号模型
在sin-FDA非线性频偏信号的基础上,单个阵元发射多频信号,则Δfn=Δfsinn,n=0,1,…,N-1,Δfm=Δfsinm,m=0,1,…,M-1,其波束方向图可表示为:
(19)
3.4 square-FDA信号模型
在square-FDA非线性频偏信号的基础上,单个阵元发射多频信号,则Δfn=n2Δf,n=0,1,…,N-1,Δfm=m2Δf,m=0,1,…,M-1,其波束方向图表示为:
(20)
3.5 倒数-FDA信号模型
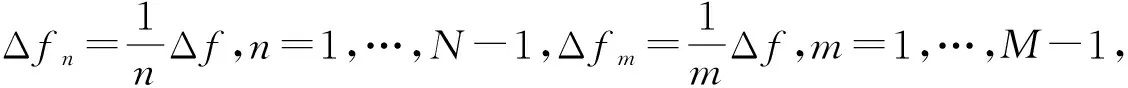
(21)
4 仿真结果
对FDA基本结构及加入非线性频偏后的FDA方向图进行仿真,仿真参数为:令f0=3 GHz,Δf=5 kHz,N=10,d=c/2f0,R′=100 km,θ′=20°,得到t=0时刻方向图如图5所示。

图5 各结构发射方向图Fig.5 The transmit pattern of each structure
由图5可以得到,在加入非线性频偏后,各种结构均能在目标位置处形成点状波束,有效消除了基本FDA中的距离角度耦合问题。但是所形成的点状波束并不规则,log-FDA结构与倒数-FDA结构形成了在距离和角度上跨度较大的“拖尾”波束,旁瓣水平较高,不易于目标的定位,但是覆盖空域面积较大;sin-FDA结构在目标位置形成了比较规则的点状波束,但同时也在其他位置处形成了增益较高的旁瓣;square-FDA结构在目标位置处形成了不规则的点状波束,由于频偏是呈平方增长,增长速度远大于其他几种结构,在基本参数相同的情况下,square-FDA形成的主波束覆盖空域面积最小,而且形成了更多的高增益旁瓣。
由于加入非线性频偏后,形成的点状波束并不规则,并且旁瓣水平较高,不利于目标的定位,考虑在此基础上,单个阵元发射一个多频率波束,基本参数设置不变,频率个数为M=10,得到t=0时刻的方向图如图6所示。
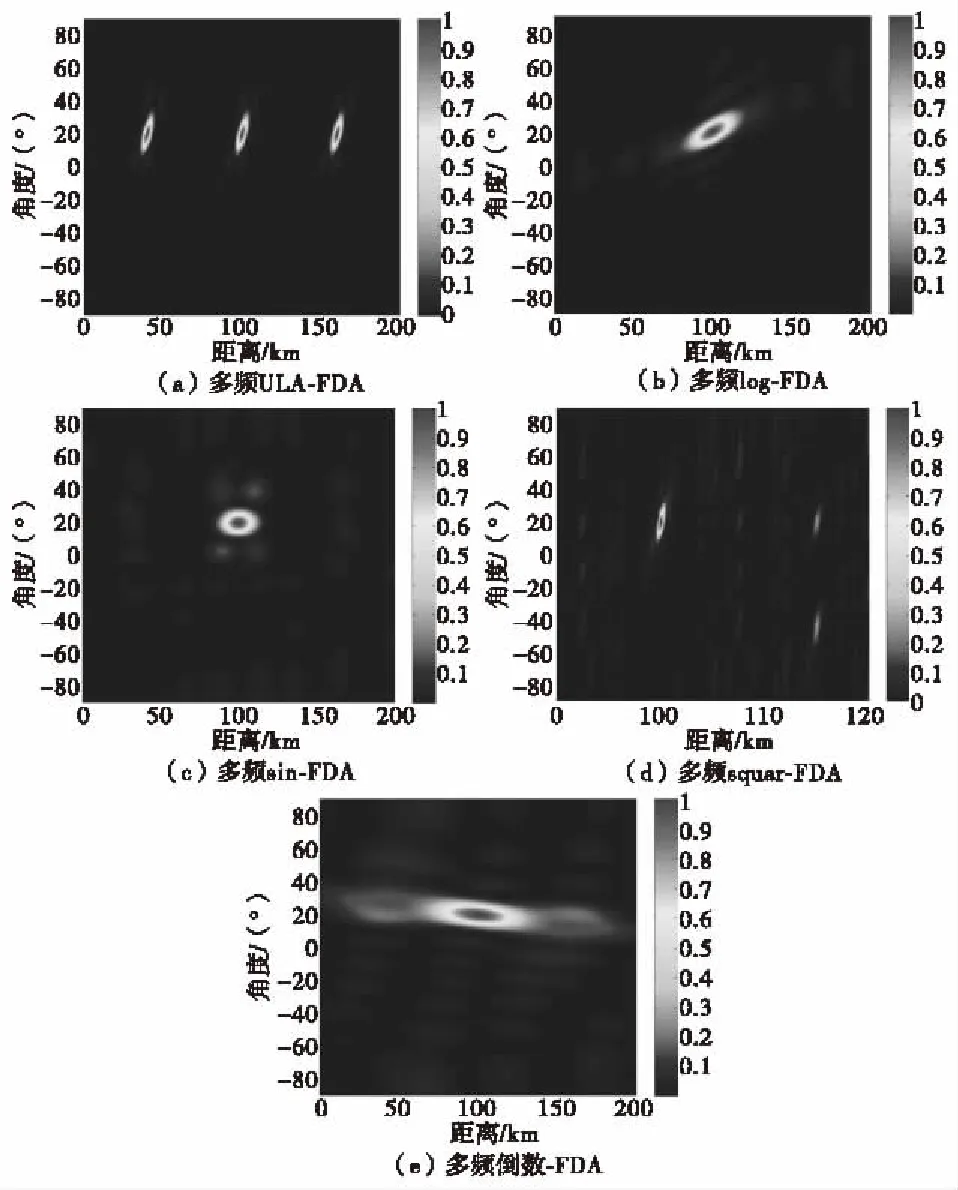
图6 多频各结构发射方向图Fig.6 The transmit pattern of each structure with multi frequency
从图6可以看出,发射多频信号对于文中各结构具有良好的点状波束形成能力,旁瓣水平较低。基本均匀线阵FDA,引入多频信号后,在距离-角度维形成了点状波束,但模糊距离和目标位置覆盖空域较小;log-FDA、sin-FDA、square-FDA、倒数-FDA点状波束形成效果较好,旁瓣低,倒数-FDA目标位置覆盖空域面积最大,square-FDA目标位置覆盖空域面积最小。
5 结论
本文提出了基于非线性频偏的频控阵点状波束形成方法。该方法通过在各阵元间分别引入呈log函数分布、sin函数分布、平方分布和倒数分布4种非线性频偏实现。仿真结果表明,4种方法均能在目标位置处形成点状波束,消除了波束图距离与角度之间的耦合。采用单阵元发射多频信号方法解决非线性频偏引入带来的旁瓣增益高的问题,仿真结果表明,该方法改善了波束形状,有效降低了旁瓣增益。

