基于专家集成赋权-灰色聚类法的引信抗干扰效能评估
柳李鹏,曹 菲,毋 凡
(火箭军工程大学,陕西 西安 710025)
0 引言
无线电引信是通过发射接收无线电波来获得目标距离信息而决定弹药起爆时刻的近炸引信[1],在各型号导弹武器装备中得到了普遍应用。随着干扰技术手段的不断发展和外界环境的飞速变化,当今战场对无线电引信的效能要求与日俱增。因此,如何精确、可行地对无线电引信的抗干扰效能开展评估成为了一个迫切需要被攻克的难题。
本文吸纳多属性群决策[2]的思想并运用至无线电引信的抗干扰效能评估当中。在群决策中,如何客观准确地确定专家的权重直接关系着方案决策结果的信服力,就本文而言,即直接关系着引信抗干扰效能评估结果的客观性、准确性。目前,关于专家权重确定的研究成果很多,Ramanathan[3]通过对群体成员之间重要性或影响力的两两人际比较来确定专家的相对权重,从本质上确定了专家成员的主观权重,具有很强的实践价值。马永红等人[4]提出了基于离差最大化的专家权重确定方法,该方法能够自动确定各评价指标间的加权系数,且不具有主观随意性。Yue在2011年提出了基于 TOPSIS 理论的确定专家权重的方法[5],即通过每个专家与正、负理想解之间的距离计算相对贴近度,确定了专家的权重,从而避免了区间数的比较和排序,既能反映群体的客观信息,又能反映决策者的主观考虑。Yue在2012年提出了通过度量个人决策与理想决策的欧氏距离以确定专家的权重,并给出了一种采用乐观系数的人性化决策方法[6],弥补了扩展TOPSIS方法的不足,该方法适用于任意数量的专家和决策方案,特别适用于复杂的多属性群决策问题。Xu等人[7]从最小化群体不一致性的角度,建立了基于专家个体同群体之间偏差函数的广义非线性优化模型,并采用遗传算法对该模型进行了求解,该模型可以充分利用每个决策矩阵中包含的所有偏好信息,尽可能地降低群体间的不一致性。闫书丽等人[8]提出了基于灰色关联度最大化的专家权重求解模型,从群体意见一致性和信息分布两方面确定了专家的权重系数,在实际应用中更为合理。以上关于确定专家权重的研究多是基于单一方法或模型,这些方法往往各具侧重点及偏好性,不足以在所有情况下的均反映真实权重;对指标数据的量化评估往往采取自定义隶属度函数的方式,导致主观性、随意性大。
本文针对上述文献存在的问题,基于无线电引信抗干扰效能评估指标体系,集成矩阵相似度、熵权及灰色理论思想,提出了专家集成赋权-灰色聚类评估方法。
1 无线电引信抗干扰效能评估指标体系构建
综合考虑引信工作环境的特殊性,常规雷达常用的抗干扰效能评估指标往往不适用于引信。因此,应当紧密结合无线电引信的工作环境及特性,综合考虑科学性、独立性、完备性、可测性选取能够从不同角度反映不同干扰对无线电引信作用效果的指标。
1.1 对应于压制性干扰的评估指标
1)干扰功率因子
在无线电引信输入功率不变的条件下,干扰功率因子是指敌方干扰设备在设定距离对我方无线电引信进行压制性干扰时,成功干扰使我方引信无法输出标高信息或精度不满足要求时所需的最小功率Pjmin与其最大功率P0之比,以KP表示。
KP=Pjmin/P0
2)灵敏度退化因子
灵敏度退化因子[9]表示在无干扰条件下发现目标所需要的最小输入功率之比。在一定间距上,无干扰条件下,令其发现攻击对象所要求的最低功率为Smin,当施加有意干扰后,其发现攻击对象所要求输入的最低功率为Sjmin,则灵敏度退化因子KSD即可表示为:
KSD=Smin/Sjmin
3)目标截获距离因子
目标截获距离定义为在一定功率的压制干扰下无线电引信截获到目标回波信号并给出标高信息的最大距离,用R表示。在无干扰条件下引信的最远探测距离用R0表示,目标截获距离因子定义为两者比值,记为:
Kr=R/R0
4)目标发现概率因子
一般来说,引信的抗干扰效能越好,则干扰设备对其发现目标的负面作用越小[10],因此可借助对比不同条件下目标发现概率的改变来表征其抗干扰效能[11]。在不施加有意干扰、并且其他条件一定时,设引信的目标发现概率为Pf,在施加有意干扰后,目标发现概率降低为Pfj,则无线电引信的目标发现概率因子Kf可记为:
Kf=Pfj/Pf
1.2 对应于欺骗性干扰的评估指标
1)标高精度退化因子
标高精度即为无线电引信在工作中产生的标高误差。在其他条件一定时,施加一定强度的欺骗式干扰前后的引信标高误差分别为E0和Eθ,定义标高精度退化因子为:
Kθ=(Eθ-E0)/E0
2)转发增益因子
转发增益主要针对转发式欺骗干扰,后者主要通过干扰机接收引信的辐射能量并进行分析和判断,调制出类似于目标出现的信号,而后放大转发给引信。转发干扰机干扰成功所需条件与干扰机的功率绝对值无关,只取决于转发增益[12]。因此,定义转发增益因子为在引信输入功率及距离等条件一定时,敌方干扰机成功干扰使我方引信无法输出标高信息或精度不满足要求时所需的最小转发增益Kjmin同其最大转发增益K0的比值,用KG表示。
KG=KjGmin/KjG
3)抗假目标欺骗干扰成功率
距离假目标欺骗干扰通过对无线电引信信号的时延调制或转发形成欺骗信号,经过无线电引信中放和检波后,产生若干个欺骗诱饵,迫使无线电引信进行目标选取,以此降低无线电引信对实际靶标的毁伤概率[13],因此,在诱饵数量一定的条件下,定义抗假目标欺骗干扰成功率为Panti-f,即:
其中,n为干扰总次数;ne为有效抗干扰次数。
1.3 指标体系的构建
依据指标体系的构建原则,从引信对抗技术角度出发,将对抗不同样式干扰的能力作为无线电引信抗干扰效能评估体系的一级因素,相对应的指标为二级因素。从而构建抗干扰效能评估指标体系,如图1。
2 问题描述


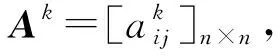
(1)

Xk=W·Dk
(2)
进而得到专家群最终的评分结果为:
(3)
此种方法即为较为简易直接,但计算过程中忽略了专家意见与群体意见不一致的问题,可通过各专家给出的判断矩阵之间的余弦相似度来度量其偏离整体意见的程度;此外,还应该考虑各决策者评分向量的信息量对最终评估结论的作用力,信息量大,则表示该专家对最终评估结果的影响能力大,可用信息熵来度量。对于抗干扰效能的评估,还应量化确定其最终评定等级,可通过灰色聚类理论来确定其灰色聚类系数。
3 基于专家集成赋权-灰色聚类的评估方法计算步骤
3.1 基于矩阵相似度的专家权重计算
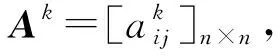
要推动全面清理不利于民营企业发展的法律法规和规范性文件。统筹协调正在开展的相关法律法规清理工作,推动在2018年年底前集中清理现行法律法规和规范性文件中有悖于平等保护原则、不利于民营经济发展的相关内容,打破各种“卷帘门”“玻璃门”“旋转门”。进一步加强法规规章备案审查,及时纠正有悖于保护民营经济的法规规章规定,积极为民营企业发展提供平等法治保障。
本文使用余弦法测算专家判断矩阵间的相似度。定义专家ek,ek′的判断矩阵Ak,Ak′的各行相似度为:
(i=1,2,…,n,k,k′=1,2,…,l)
(4)

(k′≠k,k=1,2,…,l)
(5)
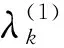
(6)
但一味的追求群体意见的一致性往往会忽略少数有着丰富经验的专家给出的建设性决策意见,下面使用熵权法对决策者的权重做进一步的调整。
3.2 熵权的计算
信息熵理论是在1948年由Claude Elwood Shannon从热力学引入信息论领域的,代表着不确定度的度量[15]。在一个系统中,信息熵代表着该系统的紊乱程度。根据信息熵的定义,当某系统的n状态出现的概率各为pi(i=1,2,…,n)时,系统的熵为:
(7)
规定当pi=0时,pilnpi=0。由信息熵理论可知,当该系统置于各状态的概率相同时,即pi=1/n,系统的熵值最大,即为H(1/n,1/n,…,1/n)=lnn,此时表示混乱的程度为最大。由该规则可知,各位决策者的熵值大即表示该决策者对各属性的评分差异化小。本文认为,某一专家对不同指标的决策结果越为接近,则该专家的评分向量中对评估结果的有影响能力的信息量就越少;反之,若对不同指标决策结果差异较大,则认为该专家对评估结果的影响能力就越大,即应当赋予该专家更大的权重。如此,可以激励决策者进行更为真实有效的评价。

1)对专家的评分结果进行规范化处理,计算方法为:
(8)
2)计算专家的熵,公式如下:
(9)
式(9)中,Hk代表专家ek的熵值。
3)计算专家的熵权,公式如下:
(10)
3.3 集成权值的计算
考虑到以上两种专家权重的确定方式实际上是对专家给出的决策信息的不同侧面的处理利用,两者的结合可以相互弥补单一方法的缺点和局限性。采用下式对决策者的权重做以重新规定
(11)
式(11)中,0≤u≤1。u越大,表示越重视决策者群体意见的一致性;u越小,表示越重视决策者个人决策意见的信息量;μ越大,表示越重视决策者客观权重,μ越小,表示越重视决策者主观权重。在实际运用中,通常适中选取u,μ值。于是,各指标权值即可表示为:
(12)
3.4 灰色聚类结果的计算
结合决策者集成权值及各指标评分结果向量可得到各指标综合评分向量为
(13)
在灰色聚类方法中,各属性评价值即为白化数,而该白化数相对于不同灰类的隶属程度需要通过白化权函数来度量。灰色聚类算法中的白化函数一般有三种形式[16],如图2所示。
白化权函数的转折点xi即为阈值,针对以上三种形式,函数的表达式可分别写为:
1) 图2(a)表示下限测度白化权函数,其对应的灰数⊗a∈[0,x1,x2],则
(14)
2) 图2(b)表示下限测度白化权函数,其对应的灰数⊗b∈[x1,x2,x3,x4],则
(15)
3) 图2(c)表示下限测度白化权函数,其对应的灰数⊗c∈[x1,x2,],则
(16)
将综合评分向量D代入白化权函数并做归一化处理后得到了指标i对应于灰类t的灰色聚类权为:
(17)
则聚类系数计算公式如下所示:
(18)
式(18)中,ωi为第i个指标的集成权重;di为专家群体对第i个指标的评分值;σt(t=1,2,…,s)为灰色聚类权。则采用专家集成赋权—灰色聚类法评估得到的最终评估结果为:
E=σ·CT
(19)
依据评估结果对应的评价等级区间即可确定评估对象抗干扰效能的所属等级。
4 应用实例
为了验证本文提出的基于专家集成赋权-灰色聚类法对无线电引信抗干扰效能评估的可行性和优越性,通过本实验室的“无线电引信半实物仿真平台”提取仿真数据算得相应指标检测值,结果如表1所示。

表1 单项指标数据

D1=(8.5,8,6.5,6,7.5,7,6),
D2=(9,8.5,8.5,6.5,9,7.5,7.5),
D3=(8.5,7.5,8,8.5,8.5,8,7),
D4=(9,8.5,8.5,9,7.5,9,8.5),
D5=(7.5,9,8,7.5,9,8.5,7.5)。
4.1 基于矩阵相似度的专家权重计算
根据抗压制干扰指标和抗欺骗干扰干扰指标的判断矩阵,按式(4)—式(6)得出专家权重为:


加权平均后得到基于判断矩阵相似度的专家权重分配为:
λ(1)=(0.203 5,0.203 4,0.192 8,0.202 3,0.198 0)。
4.2 专家熵权的计算
根据专家的评分矩阵Dk按式(8)—式(10)分别计算熵权,得到专家熵权分配为:
λ(2)=(0.386 5,0.278 6,0.108 1,0.081 3,0.145 6)。
4.3 集成权重的计算
取u为0.6,μ值为0.5,按式(11)计算的到专家集成权重为:
λ=(0.306 1,0.255 4,0.113 5,0.178 2,0.146 8)。
而后由专家给出的判断矩阵分别求得各专家赋予抗压制干扰指标和抗欺骗干扰指标的权重Ws,Wd为:
根据专家集成权重值,依据式(12)确定指标权重为:
Ws=(0.259 7,0.106 3,0.484 7,0.149 4),
Wd=(0.112 3,0.557 1,0.330 6)。
4.4 灰色聚类结果的计算
依据式(13)可得指标综合评分向量为:
Ds=(8.570 2,8.307 0,7.757 7,7.166 3),
Dd=(8.216 9,7.817 9,7.162 4)。
确定灰色聚类等级数为5,而后依据式(14)—式(16)分别确定对应于不同灰色类别的白化权函数表达形式如下:
1) 评价灰类为“优秀”,其对应的灰数设置为:⊗1∈[0,8,9,),白化权函数即为:
2) 评价灰类为“良好”,其对应的灰数设置为:⊗2∈[0,7,8,9,10,),白化权函数即为:
3) 评价灰类为“中等”,其对应的灰数设置为:⊗3∈[0,6,7,8,9,),白化权函数即为:
4) 评价灰类为“合格”,其对应的灰数设置为:⊗4∈[0,6,7,8,),白化权函数即为:
5) 评价灰类为“不合格”,其对应的灰数设置为:⊗5∈[0,6,7,),白化权函数即为:
将Ds、Dk分别带入函数中,依据式(17)—式(18)得到灰色聚类系数分别为:
σs=[0.089 9,0.378 8,0.410 2,0.121 3,0]
σd=[0.012 4,0.306 8,0.487 7,0.193 2,0]
咨询专家意见,将抗压制干扰能力和抗欺骗干扰能力分别赋权为W=(0.4,0.6),则最终聚类系数为:σ=[0.043 4,0.335 6,0.456 7,0.164 5,0]。
由式(19)得最终评估结果为:E=σ·CT=7.758 6。评估等级为“中等”,与仿真设定吻合。作为比较,本文采用文献[17]中未经过专家集成赋权的GAHP模型得到的评估值为8.459 2,评定结果为“良好”;采用文献[9]中的模糊综合评判模型得到的评估值为8.119 5,评定结果为“良好”。两模型所得结果与仿真设定均不符。究其原因,在于本文结合群决策的思想对评估指标的重要性判断、评分能够充分利用不同专家提供的信息,同时还考虑到决策者群意见的一致性和决策者个人意见的建设性,克服了一般GAHP模型和模糊综合评判模型在指标赋权、隶属度函数设定时的主观性、随意性,所得到结果更为客观、精确。
5 结论
本文提出了基于专家集成赋权-灰色聚类的无线电引信抗干扰效能评估方法。该方法首先基于已有理论成果建立了评估指标体系;而后采用基于判断矩阵相似度和信息熵的集成赋权法分配不同专家相应的权重值,进而得到各指标权重即灰色聚类权;最后,通过灰色聚类法对各指标按聚类权进行量化评估。应用实例表明,该方法具有可行性且相对于其他评估方法更为精确,为定量研究引信的抗干扰效能提供了一个更为客观、准确的途径。

