基于二阶中心差分滤波的高斯混合粒子PHD多目标跟踪算法
冉星浩,陶建锋,贺思三
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
目标跟踪在民用及军事层面均有普遍运用,例如飞机和船舶跟踪等。这其中,多目标跟踪问题更是当前讨论的关键问题[1-2]。然而在复杂环境下,由于目标的数目未知且变化、漏检以及噪声等因素的影响,使得多目标跟踪与单目标跟踪相比难度较大[3]。
传统的JPDAF算法以及多假设法由于计算量太大、关联不精确等问题难以有效解决多目标跟踪问题。2000年之后,Mahler提出了基于随机有限集的概率假设密度的滤波方法(PHD)来解决多目标跟踪问题[4],相比于传统的JPDAF算法,PHD算法不仅避免了复杂的数据关联过程,同时还显著提高了跟踪效果和实时性。
PHD算法目前可以分为两种:一种是高斯混合PHD(GM-PHD)[5],这种算法建立在噪声模型为高斯模型,受限于噪声模型,同时会出现计算精度较低的问题。文献[6]提出了粒子PHD算法(PF-PHD),适用于非线性非高斯情况下,不受噪声模型限制同时精度较高,但是计算量较大,会出现滤波发散的情况使得跟踪效果往往达不到要求。文献[7]提出了高斯混合粒子PHD(GMP-PHD)滤波方法,这种方法综合了以上两种PHD算法优点,使得跟踪效果有了较大地提高;但是,这种方法最大的弊端就是未融入量测值提供的信息,这样会使得所得到的样本与目标的后验概率所得到的样本之间偏差十分明显, 大大影响滤波的效果。
本文针对此问题,提出了基于二阶中心差分滤波[8]的高斯混合粒子PHD多目标跟踪算法 (简称为S-GMP-PHD)。该算法在高斯混合粒子PHD滤波的基础之上,通过二阶中心差分滤波产生最优的建议分布,然后从中采样,这样得到的重要性密度函数[9]可以最大程度地融入最新的量测信息。
1 算法原理
1.1 标准粒子滤波算法
粒子滤波算法起源于蒙特卡罗思想,适用于任何形式的状态模型[10]。其实质是通过对重要性密度函数采样得到一组随机样本来近似目标后验概率密度函数,得到的样本称为粒子[11],然后根据公式计算粒子权值,用粒子和权值加权得到样本均值代替贝叶斯估计中的积分运算得到目标状态估计[12]。
1.2 二阶中心差分粒子滤波算法
二阶中心差分粒子滤波(SCDPF)算法利用二阶中心差分滤波算法产生最优的重要性密度函数[13],可以最大程度地融入最新的量测值,这样有利于提高粒子滤波的稳定性和滤波精度,并且算法计算量较小。SCDPF算法具体步骤如下:
1)初始化:k=0。

(1)
(2)
2)二阶中心差分滤波:k=1,2,…,N。
①根据公式计算得到每个粒子的一阶均差矩阵:
(3)
(4)
(5)
(6)

(7)
③更新预测误差协方差矩阵:
(8)
④根据下式计算出每个粒子的二阶均差矩阵:
(9)
(10)
(11)
(12)
⑤预测量测方程:

(13)
预测误差交叉均方矩阵为:
(14)
Kalman滤波增益为:
(15)
(16)
更新每个粒子的协方差估计:
(17)
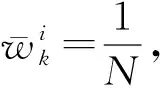
(18)
(19)
(20)
2 PHD滤波算法
2.1 PHD滤波原理
PHD滤波分为预测和更新[14]两步:
1)预测
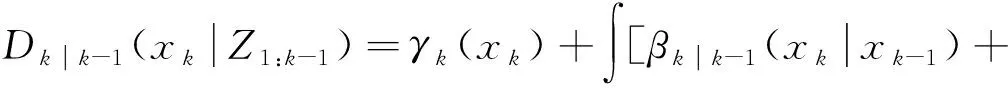
(21)
2)更新
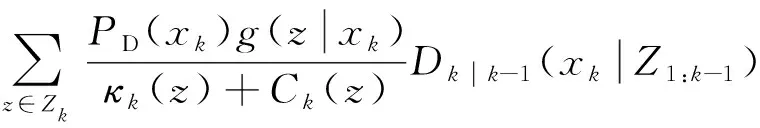
(22)
式(21)、式(22)中,βk|k-1(xk|xk-1)为衍生目标的强度,γk(xk)为新出生目标的PHD,ek|k-1(xk-1)fk|k-1(xk|xk-1)为存活目标的强度,ek|k-1(xk-1)为目标存活概率,fk|k-1(xk|xk-1)是目标的状态转移概率;PD(xk)为检测概率,g(z|xk)为目标似然函数,κk(z)为杂波强度。
2.2 GMP-PHD滤波
传统的高斯混合粒子PHD滤波利用一组高斯项相加来近似目标的概率分布[15],分为预测和更新两步。
1)预测
Dk|k-1(x)=Ds,k|k-1(x)+Dβ,k(x)
(23)
(24)
(25)
对高斯项采样得:
(26)
式(24)中,
(27)

(28)
化简可得:
(29)
2)更新
GMP-PHD滤波中似然函数为:
g(z|x)=N(z;h(x),R)
(30)
更新方程为:

(31)
(32)
(33)
(34)

(35)
GMP-PHD算法综合了两种PHD算法的优点,使得滤波精度得到了大大提高,但是由于在重要性采样过程中没有考虑到量测值,导致与真实值存在偏差从而出现精度不高、滤波发散等问题[16],这样对于要求比较高的系统,算法达不到预期的要求。因此,提出了改进的S-GMP-PHD算法。
2.3 改进S-GMP-PHD算法步骤
结合SCDPF算法和上述GMP-PHD滤波方法,改进S-GMP-PHD算法的步骤描述如下:


3)粒子的预测和更新:采样后根据样本状态和权值进行预测,再利用量测值对预测值进行更新,步骤如下:
(36)
(37)
(38)
(39)
(40)
(41)
(42)
(43)
(44)
(45)
4)权值递推:
(46)

(47)
5)PHD的预测与更新:
Dk|k-1(x)=Ds,k|k-1(x)+Dβ,k(x)
(48)
式(48)中,
(49)
(50)
化简可得:
(51)
PHD更新为:

(52)
权值更新为:
(53)
6)目标个数估计和更新:
(54)
(55)
3 仿真结果与分析
为了验证本文所提算法优越性,分别用GMP-PHD和S-GMP-PHD算法的性能进行对比分析。
3.1 仿真环境
仿真设定为二维平面区域中,跟踪的目标数目未知且变化。目标跟踪模型为:
xk+1=Fxk+Gwk
(56)
(57)
(58)
(59)

仿真中共有5个目标,设定初始时刻存在一个目标,初始状态为(-40,3,40,-1),之后有4个目标交替出现。目标以w=0.025 rad/s做曲线运动,各个目标之间运动轨迹有交叉,假设目标存活概率与检测概率均为0.99。wk是标准差方差为0.01的高斯白噪声;vk为量测噪声,方位角误差方差为0.01 rad2,距离误差方差为0.1。采样周期为1 s,仿真时间为100 s。采取最优子模型分配距离(Optimal Subpattern Assignment,OSPA)作为多目标跟踪性能的评价标准。
3.2 仿真结果分析
仿真结果如图1—图5所示。
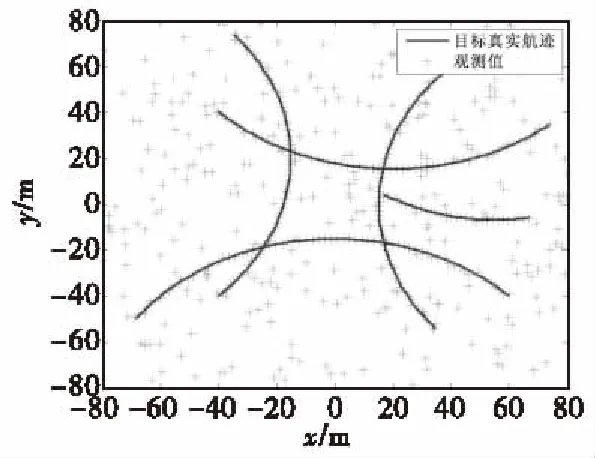
图1 目标真实航迹Fig.1 The true estimate of target

图2 GMP-PHD状态估计图Fig.2 State estimate of GMP-PHD

图3 S-GMP-PHD状态估计图Fig.3 State estimate of S-GMP-PHD

图4 OSPA距离对比图Fig.4 OSPA distance of GMP-PHD and S-GMP-PHD
图1为杂波环境下目标真实轨迹图,图2、图3和图4分别是GMP-PHD算法,S-GMP-PHD算法的状态估计图与OSPA距离对比图,图5为目标个数估计图。从图2和图3可以看出两种算法都能较好地跟踪多个目标,但是从图4可以看出S-GMP-PHD跟踪多目标OSPA距离小于GMP-PHD,跟踪精度要高于GMP-PHD。这是因为GMP-PHD算法中在高斯滤波过程中难以避免会发生累计误差的问题,同时建议分布未融入最新的量测值,S-GMP-PHD算法采取二阶中心差分滤波产生最优的建议分布,充分考虑了量测值,使得得到的重要性密度函数更加接近目标真实的后验分布,显著提高了滤波效果。

图5 目标个数估计Fig.5 Quantity of target
同时从图5看出两种算法对目标个数估计与真实的目标个数大致相同,但是GMP-PHD算法存在对目标个数估计存在较大误差的情况,改进算法对目标个数估计更加精确。
4 结论
本文从高斯混合粒子PHD滤波算法中存在的跟踪精度低和滤波发散等问题出发,提出了基于二阶中心差分滤波的高斯混合粒子PHD算法。该算法首先利用二阶中心差分滤波方法产生重要性密度函数融入GMP-PHD滤波框架中,然后进行PHD更新。仿真结果表明,改进算法能够有效地跟踪多个目标,相比于GMP-PHD滤波算法,跟踪精度大大提高,系统稳定性也得到进一步加强。
2018年引信技术创新发展研讨会暨中国兵工学会
引信专业委员会、《探测与控制学报》编委会工作会召开
2018年引信技术创新发展研讨会暨中国兵工学会引信专业委员会、《探测与控制学报》编委会工作会于2018年11月20日至23日在北海市召开,来自院校、研究所、工厂和军方等单位的近40名委员参加了会议。
中国兵工学会引信专业委员会和《探测与控制学报》编委会工作会议由引信专业委员会主任委员黄峥主持,微机电集团西安机电信息技术研究所领导致辞,委员们听取了两委会工作汇报并通过了学报2015-2016年优秀论文的评选结果,肯定了学会、学报近年的工作成绩,特别是《探测与控制学报》在国内武器类核心期刊排名稳步提高。目前《探测与控制学报》仍然保持中国科学院《中国科学引文数据库(CSCD来源刊)》(核心库),北京大学《中文核心期刊要目总览》,中国科学技术信息研究所《中国科技核心期刊》等三个评刊机构的核心位置。与会委员经过认真讨论,对学会和学报今后的工作提出建设性的意见和建议,并达成共识,确定了学会和学报2019年的工作计划。
引信技术创新发展研讨会由微机电集团西安机电信息技术研究所、南京理工大学、洛阳014中心、中物院905所等单位的专家分别对国内外引信发展现状与趋势,引信产品在安全性、可靠性方面的问题和解决方法,引信抗干扰、新技术融合等方面的创新与发展方向,以及引信在智能毁伤控制、智能安全控制等方面做了专题报告。
本次会议强调了引信在武器系统中的关键作用,针对我国引信技术与国际先进水平的差距,提出并研究当前引信技术发展的一些重点、难点问题,探讨当前引信行业的科研、生产、测试等方面存在问题的解决途径,展望引信未来发展趋势。目的是提高引信核心技术领域的自主创新能力,缩小与世界发达国家在引信技术上的差距,发展具有中国特色的引信核心技术。
与会代表们通过会上、会下各种形式的学术交流,信息沟通,对我国引信技术的现状和发展前景有了进一步的了解,为引信学术界的和谐发展营造了良好环境,为引信技术及其相关专业的工作者提供了一个高层次、综合性的学术交流平台,会议圆满结束。
《探测与控制学报》2015—2016年优秀论文获奖作者名单
任宏光 邹金龙 王海彬 尚雅玲 张龙山 李东杰
徐蓬朝 邝应龙 李豪杰 张星星 李晓晨 王辅辅
朱海洋 单体强 崔逊学 常 悦 张彦军 刘 鹏
张美绒 涂宏茂 司昕璐 赵玉清 吴英伟 齐杏林
焦志刚 朱 航 闻 泉 温竞龙 吕全通 戴宗亮
(司昕璐报道)

