基于卡尔曼滤波的多普勒速度平滑技术研究
张明宇 王艳
(上海船舶电子设备研究所,上海,201108)
在声学多普勒测速技术领域,随着水下航行器应用领域的不断扩大,性能要求的不断提高,水下导航系统出现了新的发展趋势,声学多普勒测速仪已经成为其中重要组成部分,对测速精度提出了更高的要求。在实际的应用中,测速精度主要受到两方面的影响:测速系统所需要的检测时延信号在一定程度上受到了水下未知环境噪声的干扰,导致得到的信号往往存在一定的实际误差;传播介质的不均匀性也可能会导致信号出现一定程度上的散射与起伏,致使系统无法对运动物体进行较为精确地测速。
本文通过结合水下航行器载体平台的特点,基于卡尔曼滤波的系统模型,建立卡尔曼滤波的状态方程和量测方程,并建立变加速运动模型,使用四种滤波模型对变加速运动进行较为精确的仿真,得到该条件下的最优卡尔曼滤波模型。通过该模型选取最优滤波初值和滤波参数。用实验中获得的外场数据对卡尔曼滤波的多普勒测速瞬时速度平滑的有效性进行验证。
1 卡尔曼滤波的系统模型
卡尔曼滤波技术是在时域上以线性最小方差的准则下的最优估计。其采用递推算法,核心方程是状态方程和量测方程[1]。
对于离散时间系统:
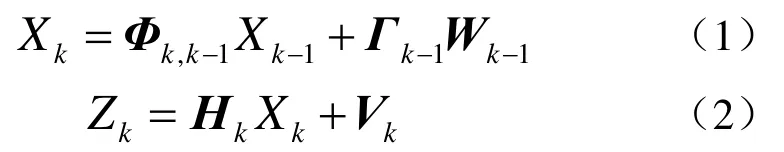
式(1)为状态方程,式(2)为量测方程。其中,Xk表示第tk时刻的被估计量,Φk,k-1表示第tk-1时刻至第tk时刻之间的一步转移矩阵,Wk-1表示系统噪声序列,Γk-1表示系统噪声驱动阵,Zk表示tk的量测量,Vk表示量测噪声序列,Hk表示量测阵。
同时,Wk和Vk满足以下关系:

式中,Qk表示系统噪声方差阵,Rk表示量测噪声方差阵,k、j表示不同的时刻。通过简单的推导,可以得出正确的卡尔曼滤波基本方程[2]:

2 四种滤波模型的性能分析
由于在实际的运动情况中,很难出现物体做加速度恒定的匀速运动或匀加速运动的理想情况,所以本文选择了加速度变化缓慢的变加速运动模型作为分析讨论的对象,并通过CV模型、CA模型、Singer模型以及“当前”统计模型进行性能分析。
2.1 CV模型
CV模型在离散时间条件下,卡尔曼滤波系统的状态方程为:

式中,xk、vk分别表示物体当前时刻的运的位移与瞬时速度,bk表示加速度的随机扰动噪声,且服从于的高斯分布,T表示系统观测时间之间的间隔时长。
2.2 CA模型
CA模型在离散时间的条件下,卡尔曼滤波系统的状态方程[3-5]:
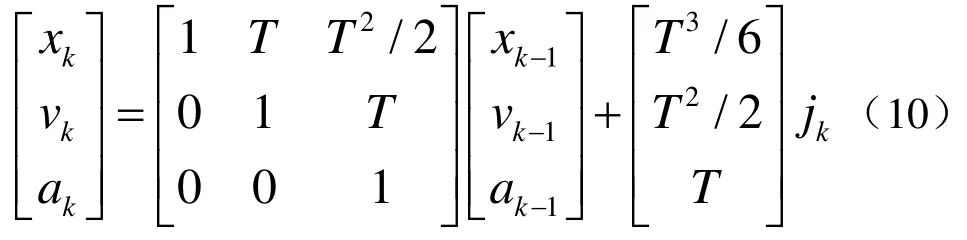
式中,xk、vk、ak分别表示物体当前时刻的位移、瞬时速度与瞬时加速度,jk表示加加速度(急动度)的随机扰动噪声,服从的高斯分布,T表示系统观测时间间隔时长。
2.3 Singer模型
Singer模型在离散时间的条件下,卡尔曼滤波系统的状态方程[6]:
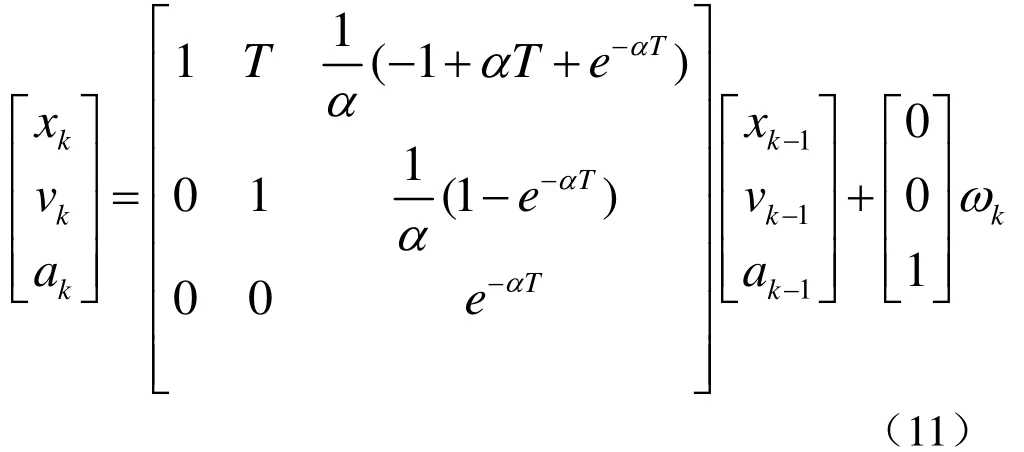
式中,ωk表示服从的高斯白噪声序列,a为机动频率。
2.4 “当前”统计模型
“当前”统计模型在离散时间的条件下,卡尔曼滤波系统的状态方程[7]:

式中,为机动频率平均值,
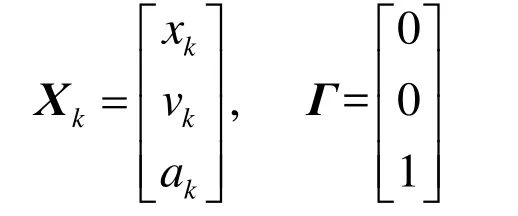

2.5 四种模型滤波的性能仿真分析
把四种滤波模型应用到变加速运动模型中,将滤波结果与真实速度之间的误差大小作为滤波性能优劣的参考标准,添加服从N(0,10–1)的高斯白噪声作为量测噪声,通过时延信息解算物体的速度,作为直接速度信息,进行仿真。
目标零时刻位置为(0 m,0 m),0~200 s内,保持匀速直线运动的运动状态,在X、Y轴分速度都为10 m/s;在201~400 s内,保持匀速曲线运动的运动状态,运动半径设定为1 000 m,线速度设定14 m/s,采样间隔1 s。
在图1中,图(a)显示了真实轨迹与测速仪测量速度添加噪声再积分后的轨迹,图(b)为图(a)的部分轨迹放大图,可以较为清晰地看到滤波前的位移和真实位移有一定的差距。观察后可以发现,测量轨迹与真实轨迹之间存在一定的偏差,这是由于添加了量测噪声所导致的。图(c)显示了经过卡尔曼滤波处理后各模型的轨迹结果,图(d)为图(c)的部分放大图。可以看出,经过卡尔曼滤波后,轨迹上的每个位置都更加接近于真实位置,能够有效地提高定位精度。
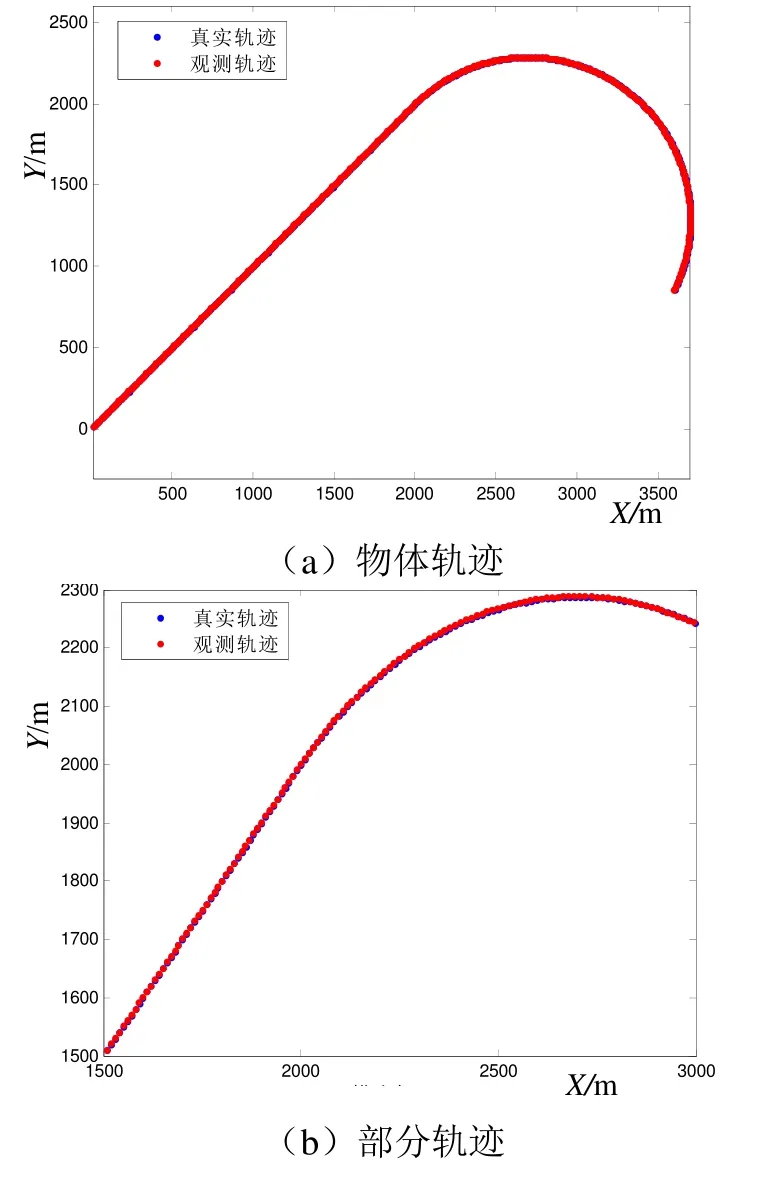
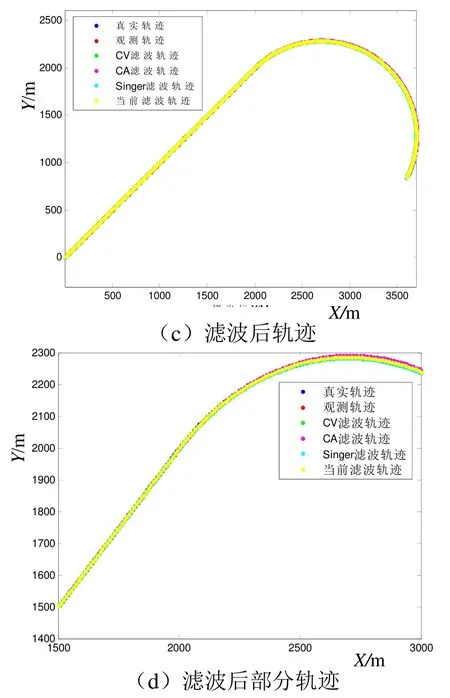
图1 滤波前后轨迹对比图
图2为各模型滤波后的各时刻的速度与真实速度之间的差值。从图中可以明显地看出,经过不同模型进行滤波,都会对速度产生一定程度的平滑,即对速度的估计精度在一定程度上提高了。CA模型的滤波效果是最好的。


图2 卡尔曼滤波速度与真实速度之比
综上,在合理选择滤波参数的背景条件下,CA模型可以满足测速精度的需求,完成速度平滑的任务。由于其对运动模型的滤波效果最好,在水下的相关系统具有更广泛的适用性。所以,选择CA模型作为系统卡尔曼滤波模型。
3 滤波初值和滤波参数的选取
3.1 滤波初值的选取
卡尔曼滤波是一种递推算法,初值X0和P0的选取相当重要,要严格保证滤波估计是无偏的,方差最小,才能实现较好的滤波效果。为了避免将第一时刻值作为滤波初值所带来的误差,选取采样值的平均值作为初值的方法,更多地利用已有的平均时延数据来计算速度值,并将时延值赋给t0,坐标均值赋给x0,并可以用这些数据来估计初始情况下的协方差矩阵P0,使其在起始阶段就有较好的滤波效果,方便操作。
以初始速度0 m/s,加速度0.02 m/s2,添加服从N(0,10–1)的高斯白噪声作为量测噪声,沿一个方向作简单的匀加速直线运动为例进行仿真。从图3、图4可以明显地看出,速度、位移的滤波均出现收敛的情况,且后段差别不大。但在初始阶段,平均值的效果非常明显地优于对方。
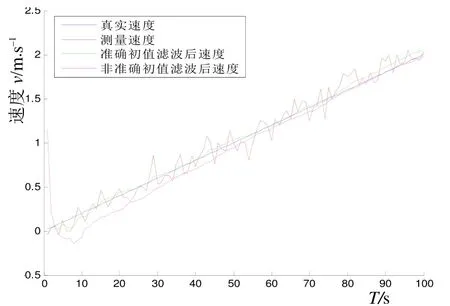
图3 不同初值滤波速度结果
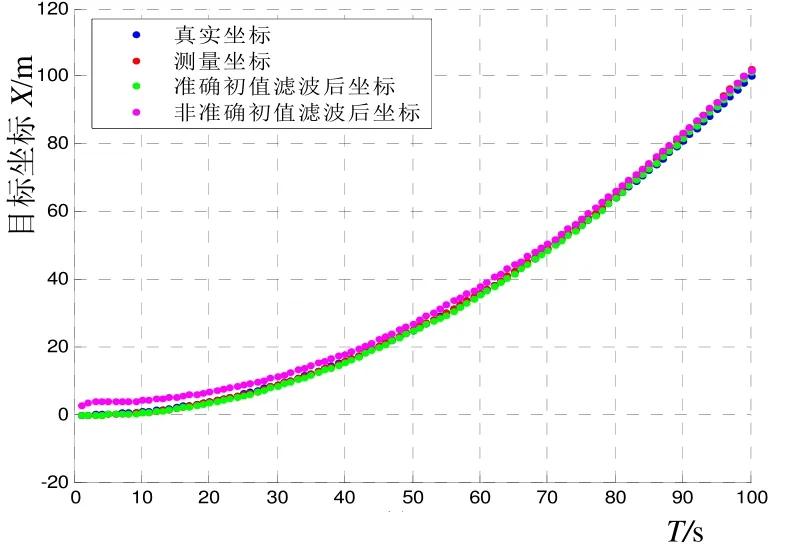
图4 改变初值后的位移结果
3.2 滤波参数的选取
系统的噪声方差阵Qk和量测噪声方差阵Rk两个参数选取的优劣将会直接地影响着卡尔曼滤波的滤波精度。通常情况下,需要在滤波前通过模拟计算来取Qk和Rk。在机动性不高时,Qk和Rk可以写作常数q和r。以匀加速运动为例,选取合适的数q和r。水下运动物体的初始位置为(0,0),X方向初速度0 m/s,加速度0.02 m/s2;Y方向初速度0 m/s,加速度0.02 m/s2,运动时间为500 s,采样间隔1 s。
3.2.1q值的选取
固定r值,q的取值递减,从10–6到10–9进行尝试。从图5可以明显地发现,q值的不同取值对效果造成了很大影响,q值选取10–7比较合适。如果q值过大,则效果不明显,滤波将失去作用;q过小,虽然误差很小,但当前测量值已经失去了原有的修正作用,随着运动的进行,可能会出现滤波发散现象。q的取值,应与统计特性相匹配。

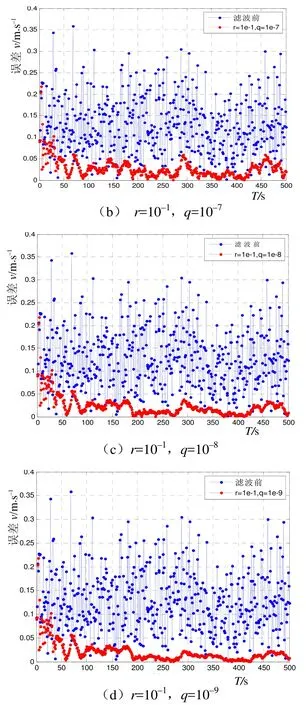
图5 q对滤波性能的影响
3.2.2r值的选取
固定q值,r的取值递减,从101~10–2进行尝试。从图6可以明显地发现,r的影响效果同q正好相反。

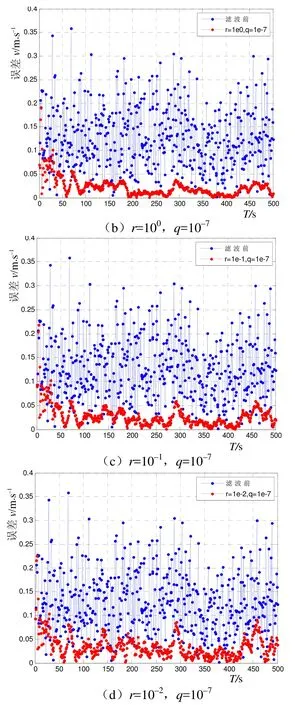
图6 r对滤波性能的影响
当r取 10–1左右时,滤波的性能达到最好;r较大,当前测量值对滤波值的修正作用比较小,随时间的累积,可能会出现滤波发散现象;r较小,比较容易引起滤波精度的降低。r选取 10–1比较合适。r的取值,应接近于量测噪声的情况。
3.2.3q/r对滤波性能的影响
q/r称为信噪比,选取r=100、q=10–7和r=10–1,q=10–8这两组参数进行比较。从图7可以明显地看出,q/r相同,通过两组参数进行滤波而得到的滤波效果是较为相同的,不同之处在于初始阶段,而r的精确程度,将直接地影响到滤波初始阶段的滤波精度以及误差的收敛速度,r越准确越好。
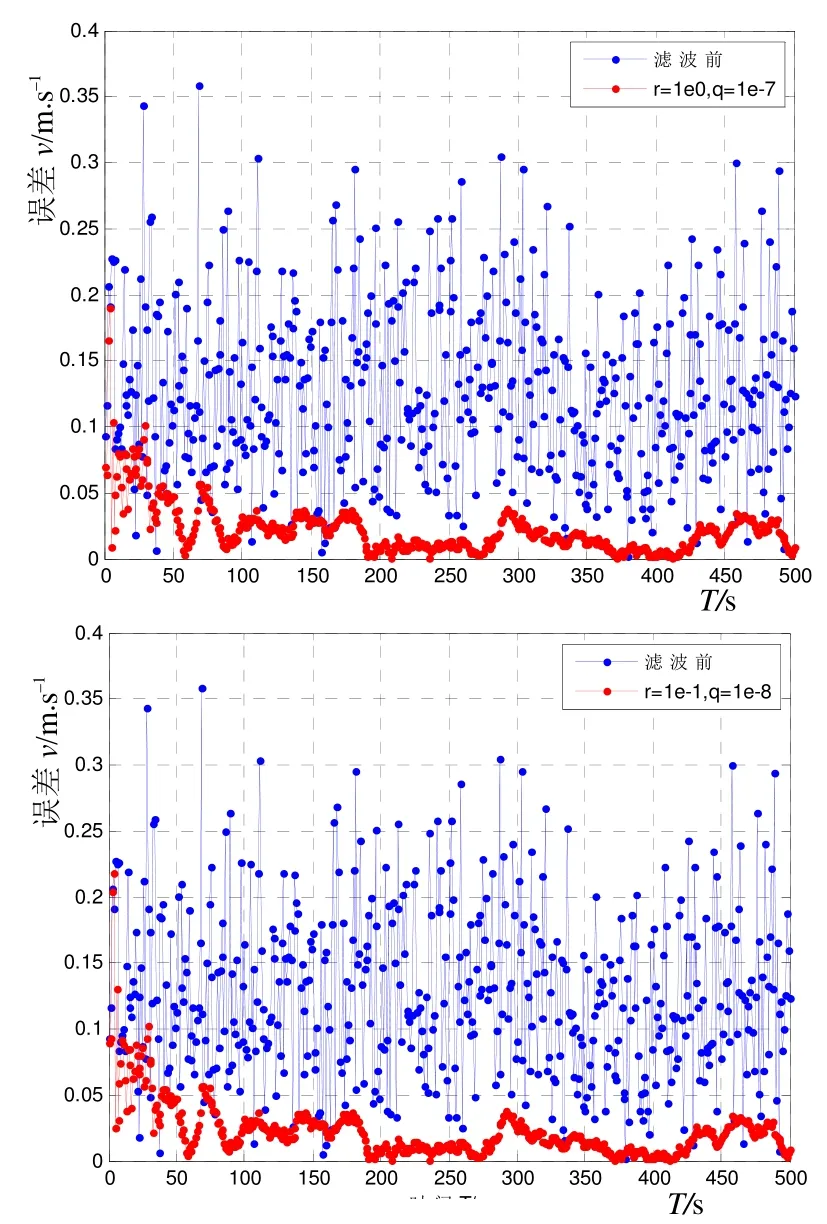
图7 q/r对性能的影响
4 试验数据验证
图8为运动物体在外场运动5 000 s、采样间隔为1 s时,多普勒测速仪测得的速度随时间变化的观测数据。通过第2节和第3节分析,采取CA模型作为滤波模型,为简便起见,选取滤波的初值速度为0 m/s,滤波参数r=10–1、q=10–7进行卡尔曼滤波。从图9和图10可以看出,测得的速度得到了相当大程度的平滑。
假设某一时刻的真实速度是当前时刻测量值与前后20个时刻的测量速度的平均值,将此真实值与滤波前及CA滤波后的值进行比较即可得到误差的大小。代入外场试验数据进行验证,通过CA模型进行滤波,从图11与图12可以看出,速度误差明显减小,证明卡尔曼滤波方法对多普勒速度平滑工作是有效的。
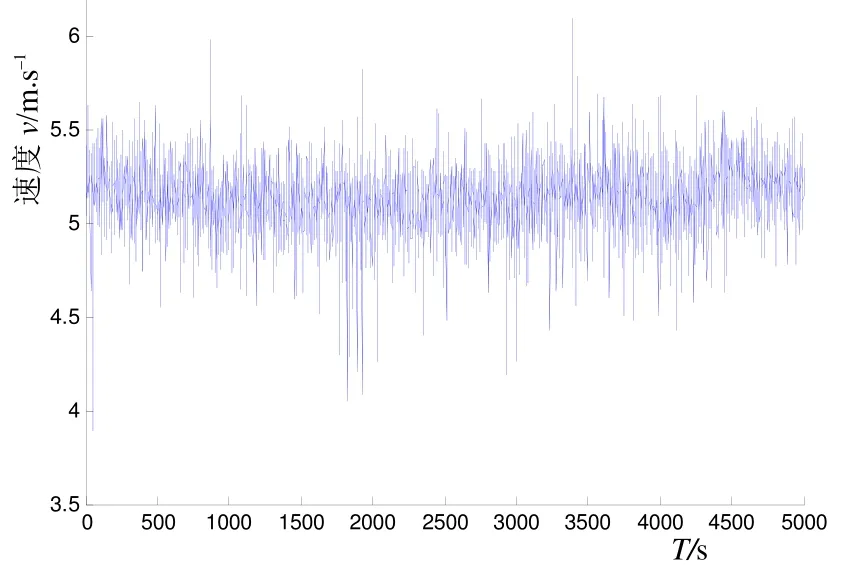
图8 测速仪测得的速度
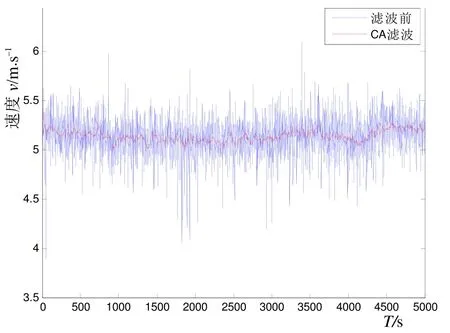
图9 速度平滑效果
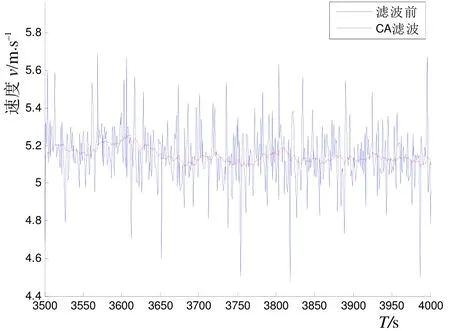
图10 部分时刻速度平滑效果比较

图11 速度平滑效果比较
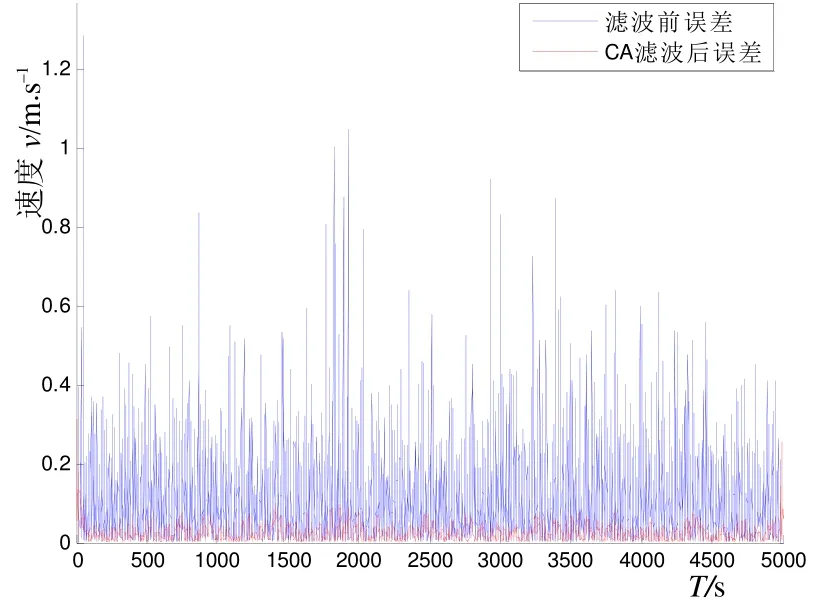
图12 测量值与CA滤波和真实值之间的误差
5 结论
工程中使用多普勒测速仪进行测速时,测速结果出现误差是不可避免的,选择合适的方法,对多普勒速度进行平滑就显得尤为重要。通过卡尔曼滤波对速度进行平滑而得到较为精确的速度值,对运动物体的定位及航迹推算有着一定的帮助及实用价值。在本文研究中,对滤波参数的选取建立在对已有文献的研究上,缺少系统的理论支撑,需要进行下一步的研究。以前的卡尔曼滤波更多地是针对位移进行研究,本文则是建立在速度平滑的基础上,对航迹等数据作进一步的推算。本文通过使用卡尔曼滤波方法,并选取合适的参数,对速度进行平滑,可以对定位起到帮助,对航迹推算也有一定作用。

