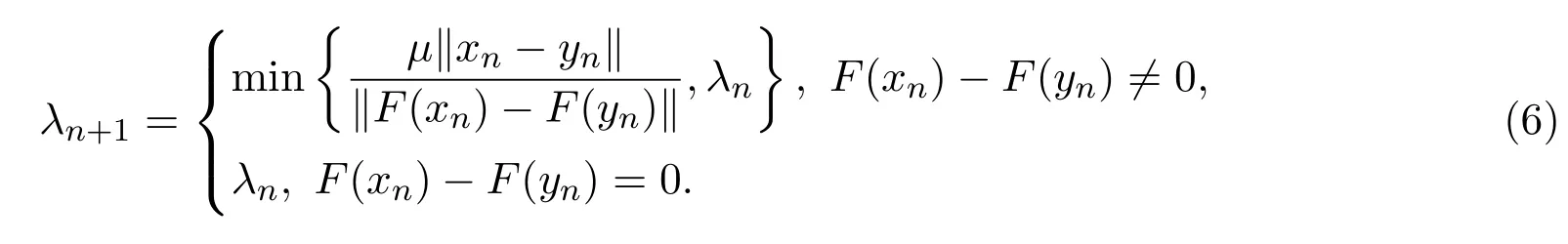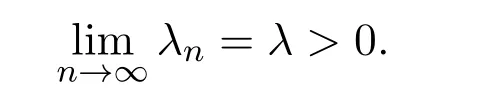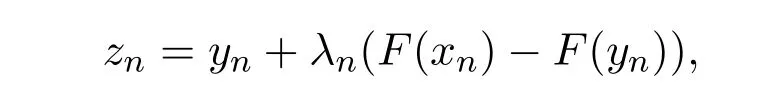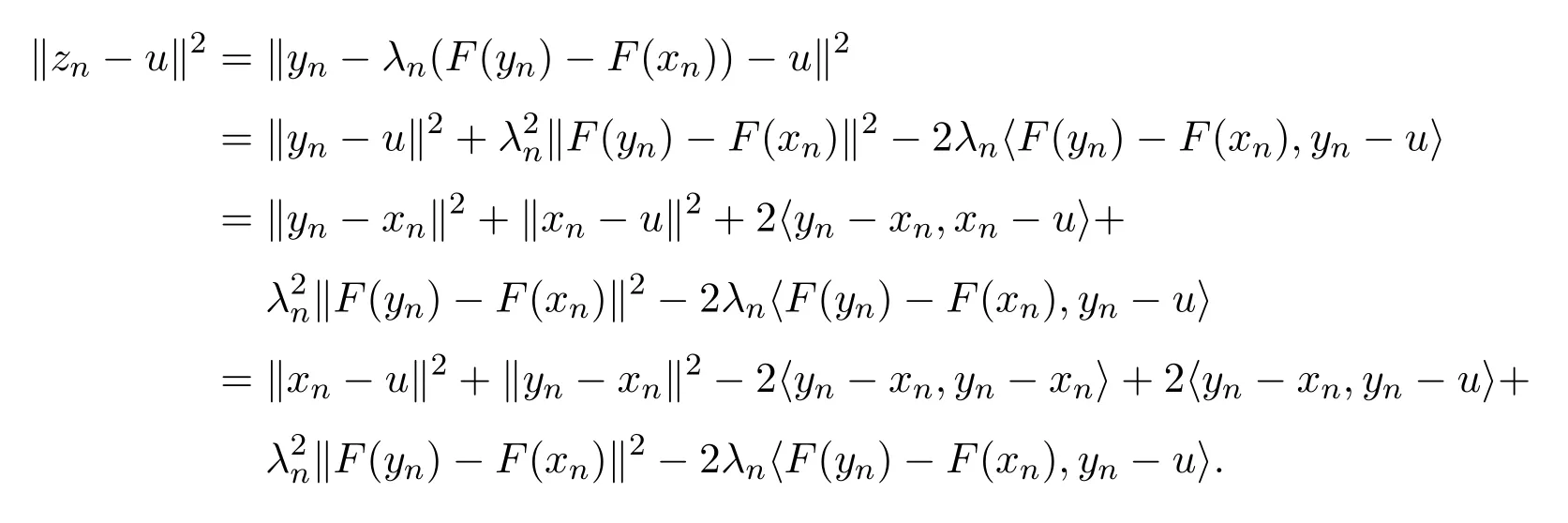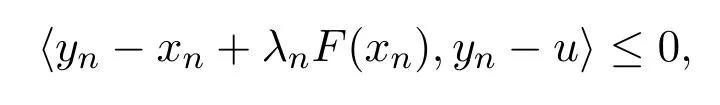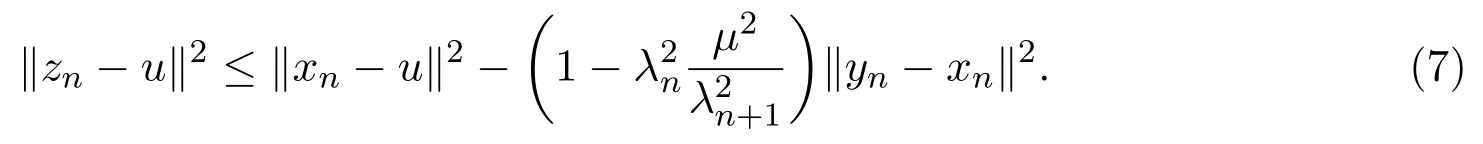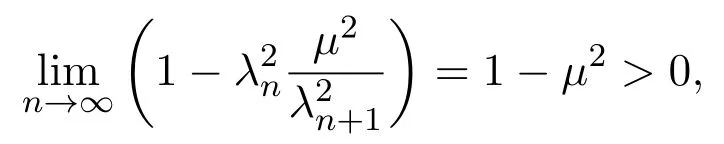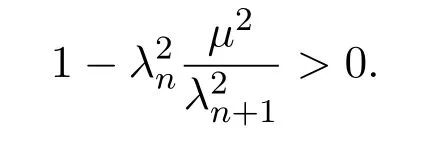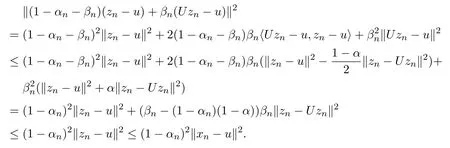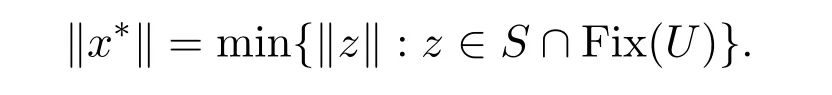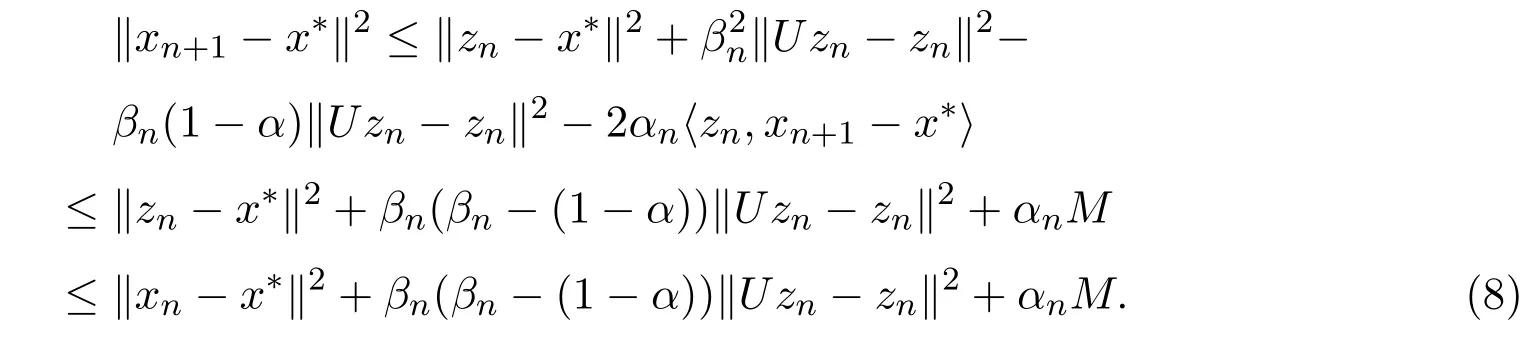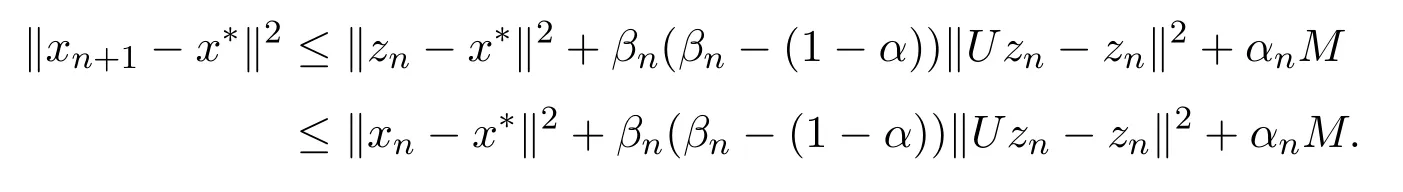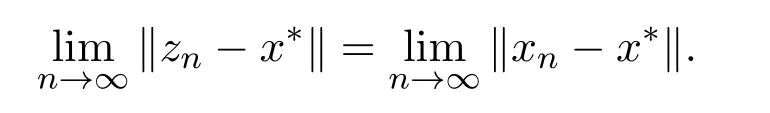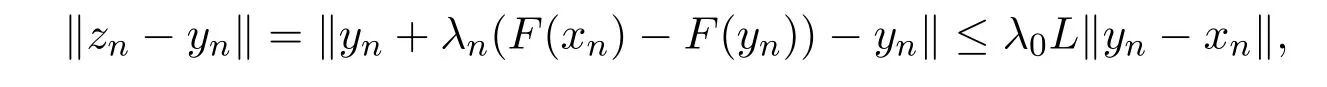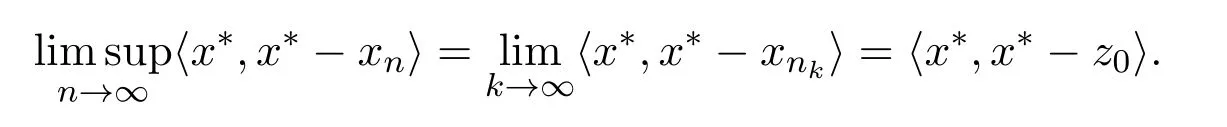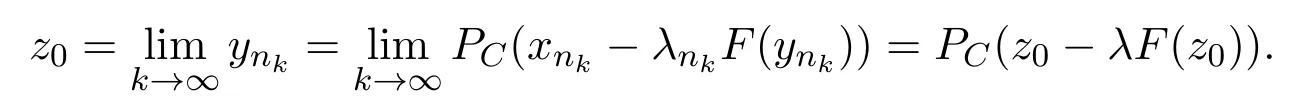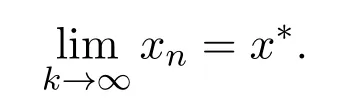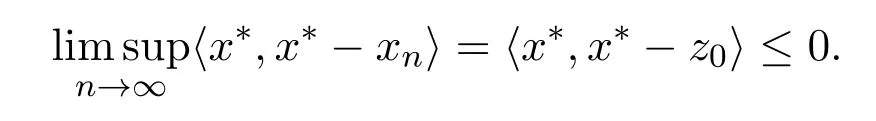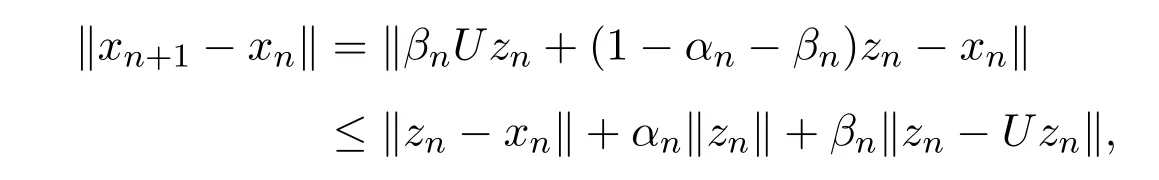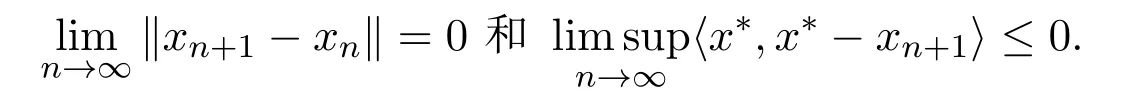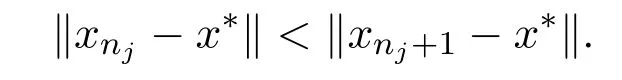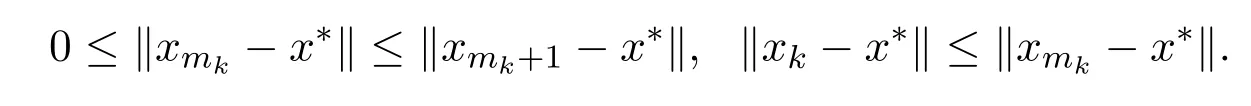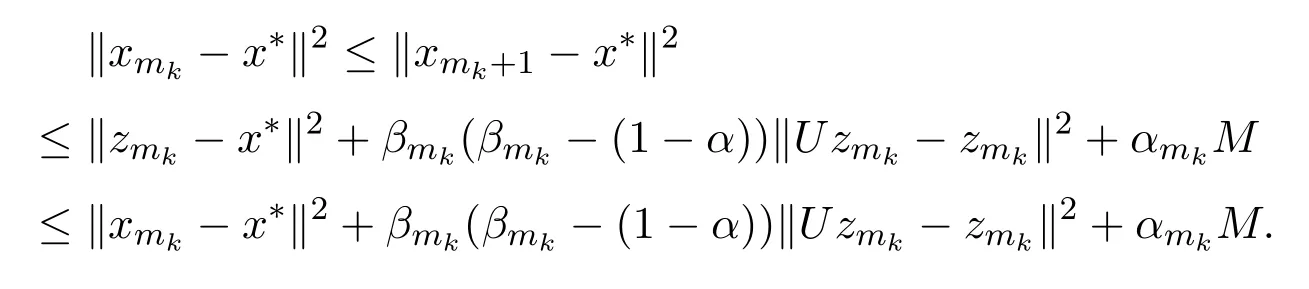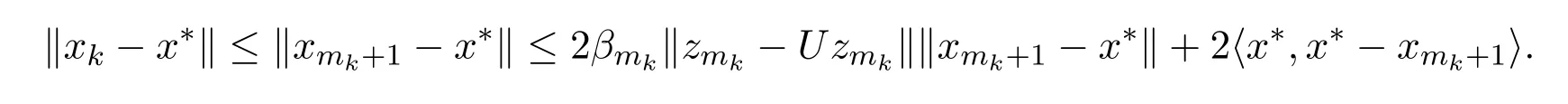一类伪单调变分不等式的投影算法
杨军刘红卫张哲
(1.咸阳师范学院数信院,陕西 咸阳 712000;2.西安电子科技大学数统院,陕西 西安 710162)
1 引言
设Rn是n维欧几里得空间,C是Rn的非空闭凸子集,分别表示定义在Rn中的内积和范数,Rn中的序列{xn}收敛于x记为xn−→x.令F:Rn−→Rn是给定的映射,变分不等式问题为:寻找x∗∈C,满足

变分不等式在物理、经济平衡理论、控制论、工程、优化等许多方面都有重要的应用,其理论和算法的研究在近几十年得到了长足的进展.对于变分不等式的算法主要有正则化方法和投影算法两种方法.但正则化投影不适用于伪单调映射情形[1].本文研究利普希茨伪单调映射变分不等式的投影算法.
设C是Rn的非空闭凸子集,x∈Rn,x在C上的投影定义为
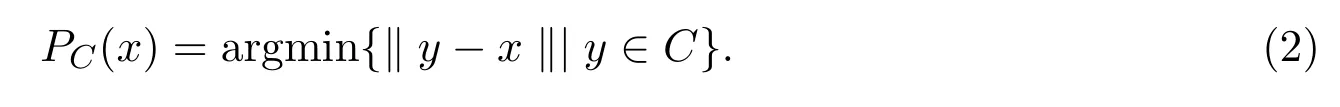
众所周知[2],对于任意正数λ,x∗是变分不等式(1)的解当且仅当

为了计算单调变分不等式,文献[3-4]给出了外梯度投影算法,在其算法中,每个迭代步需要计算两次投影.若C较复杂,则在C的投影难以计算.2000年,文献[5]给出了一种梯度投影算法,在其算法中,每个迭代步只需计算一次投影.然而,上述算法的步长与映射的利普希茨常数有关,而利普希茨常数通常难以计算或估计.为了避免估算利普希茨常数,通常的做法是用类Amjo型搜索得到步长[6-7].最近,文献[8-10]给出了单调利普希茨映射的投影算法,算法中步长的计算方法无需类Amjo型搜索.本文在文献[9]的基础上,给出了一种伪单调利普希茨映射的投影算法,并且算法的解与不动点有关.
2 相关定义与引理
定义 2.1(i)若映射F满足

则称F是单调映射.
(ii)若映射F满足

则称F是伪单调映射.
(iii)若存在常数L>0,映射F满足
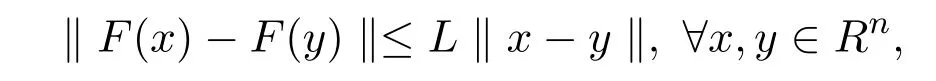
则称F是利普西茨映射.
显然单调映射是伪单调映射,反之不成立.令Fix(T)表示映射T的不动点集合,现给出下面的定义.
定义 2.2(i)若Rn上的映射T满足 Fix(T)̸=∅,且对于{xn}⊂Rn,下面结论成立

则称I−T在0点是半闭的.
(ii)设T是Rn上的映射且0≤α<1,若T满足
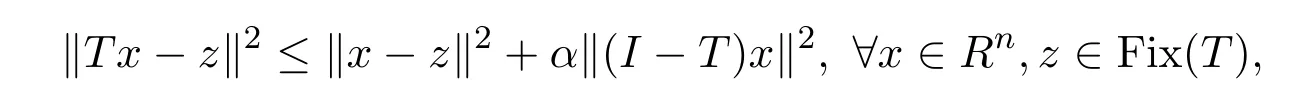
则称T是α-半压缩映射.
容易证明(见文献[11]),T是Rn上α-半压缩映射等价于

同时也等价于
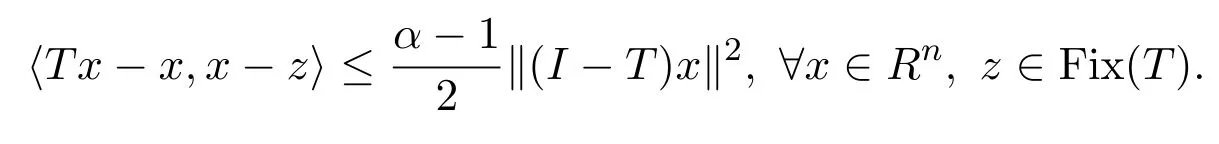
引理2.1设C是Rn的非空闭凸子集,∀x∈Rn,则
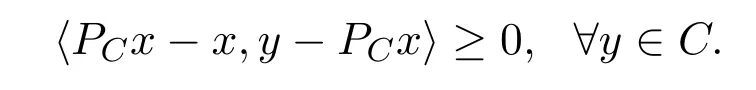
引理2.2对于任意的u,v∈Rn.则
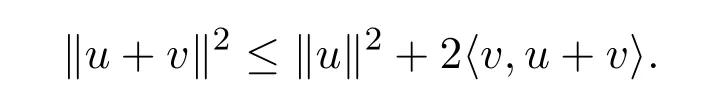
引理2.3[12]设{an}和{bn}是两个非负数列,而且满足

同时
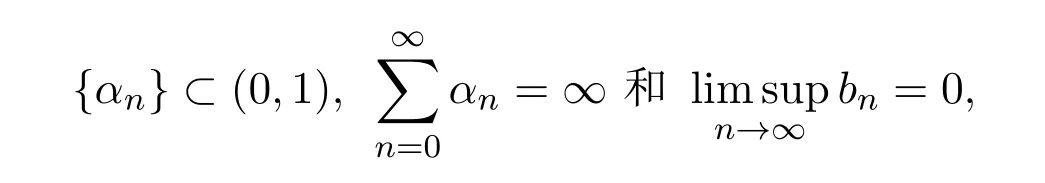
则
引理2.4[13]设{anj}是非负实序列{an}的子列,而且子列满足对于任意j∈N,成立anj 而且当k充分大时有k∈N:amk≤amk+1,ak≤amk+1.事实上mk是集合中{1,2,···,k}满足an 算法3.1 步骤1 选取λ0>0,x0∈Rn,µ∈(0,1). 步骤2 计算 如果xn=yn,停止,xn是解.否则, 步骤3 计算 令n:=n+1并回到步骤2. 引理3.1[9]设F是Rn上的利普西茨连续映射,则算法3.1产生的步长序列{λn}单调递减且有下界. 容易看出, 本文假设F是Rn上的利普西茨连续伪单调映射,U是Rn上的α-半压缩映射,I−U在0点是半闭的且变分不等式解集S与U的不动点交集非空.由文献[11]知,Fix(U)是闭凸集,从而S∩Fix(U)也是闭凸集. 引理3.2设{αn}⊂(0,1),{βn}⊂(a,b)⊂(0,(1−α)(1−αn)),则算法 3.1产生的序列{xn}是有界的. 证明令u∈S∩Fix(U),由于 则 注意到yn=PC(xn−λnF(xn)),用引理2.1,得到 即 从而得到 由于u∈S∩Fix(U),则,又F是Rn上的伪单调映射,故,从而 由于 即,∃N≥0,∀n≥N,满足 从而∀n≥N,∥zn−u∥≤∥xn−u∥.又∀n≥N, 注意到∀n≥N, 从而∀n≥N, 故序列{xn}有界.进一步得到{zn}有界. 定理3.1设,则算法 3.1产生的序列{xn}收敛到集合S∩Fix(U)中. 证明由于S∩Fix(U)是Rn上的非空闭凸子集,令x∗=PS∩Fix(U)0,则 显然x∗∈S∩Fix(U),用引理3.2,∃N≥0,∀n≥N,有.用引理2.2,则 结合序列{xn},{zn}的有界性与映射U的定义,令M为序列的上界,得到∀n≥N, 即 故 情形1若存在N2∈N(N2≥N1),满足 故 进一步有 由于{xn}有界,则存在子列{xnk}收敛于z0,同时{ynk}和{znk}也收敛于z0,并满足 从而得到z0∈S.又由于 故z0∈Fix(U),从而z0∈S∩Fix(U).下证 由于 得到 情形2若存在的子列,有 用引理2.4,存在单调递增的mk满足且对于任意的k∈N成立: 进一步有 故 从而xk收敛于x∗.定理证毕.
3 算法与收敛性证明