可压缩Navier-Stokes方程组的真空问题及研究进展

郭真华,李自来,辛周平

(1.西北大学数学学院,陕西 西安 710127;2.河南理工大学数学与信息科学学院,河南 焦作 454000;3.香港中文大学数学科学研究所,香港 新界 沙田)

1 引言

流体力学方程组是描述流体运动、发展、演化规律的宏观模型,根据质量守恒、动量守恒和能量守恒等定律推导而来.这类模型在现代应用科学中有广泛的应用,可以刻画管道中液体流动、大气流动,洋流、飞行器周围的气流等现象.可压缩Navier-Stokes方程组是一个比较典型的流体力学方程组,它们充分体现了流体力学方程组的特点和研究难点.从数学角度看,可压缩Navier-Stokes方程组是一个非线性双曲型方程与非线性抛物型方程组成的耦合方程组.由于方程组具有强非线性和退化性,使得这类方程组的研究极具困难.正因为如此,可压缩流体力学方程组长期以来吸引了许多数学家、物理学家的极大兴趣和关注.

一般地,在区域Ω⊂RN(N≥1表示空间维数)上的等熵可压缩Navier-Stokes方程组可写成如下形式:

其中ρ和U=(u1,···,uN)分别表示流体的密度和速度,e为内能,q为热通量,而 T为柯西应力张量,牛顿流体时其具有如下形式:

这里,µ和λ是粘性系数且满足

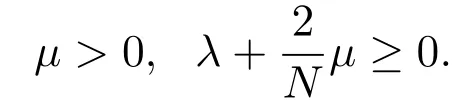
“:”记为张量的数量积,即

为T粘性部分.

当S为∇U的线性函数时,称为牛顿流,例如空气,水.当S为∇U的非线性函数时,称为非牛顿流,例如硅.

由于未知函数个数多于方程组个数(N+2方程,2N+3个未知函数),方程组(1)-方程组(2)不封闭.要封闭状态方程组,需要利用状态方程(由热力学理论得出,四个变量ρ,θ,e,P,一旦两个变量被确定,余下两个变量是已确定两个变量的函数)

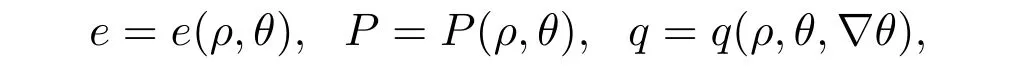
其中,θ为绝对温度.由此看出方程组(1)-方程组(2)是封闭的,未知函数是(ρ,U,θ).

本文为了简单起见,只考虑多方理想气体(例如空气,二氧化碳):

由 Fourier定律知,q=−κ∇θ,κ>0 常数.则(1)式-(2)式对未知量(ρ,U,θ)构成完备方程组.注意(1)3式可改写成

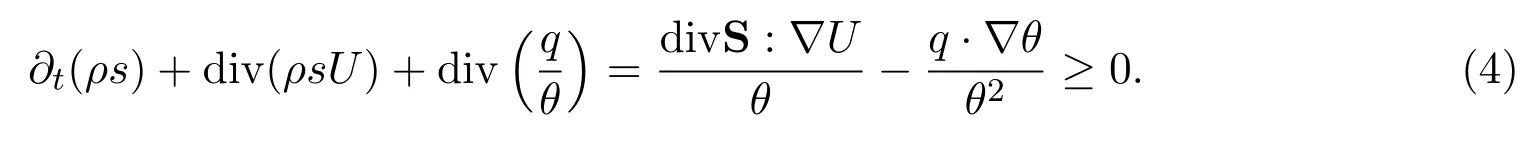
上式表明,熵的增加是由粘性和热传导引起的耗散效应引起的.如果忽略(4)式中的耗散和热传导效应,则

再由质量方程可得

因此,沿流线且在光滑解处有

称此种流为“等熵流”.由(3)式可知

于是(1)1式和(1)2式构成一对(ρ,U)的方程组,即等熵可压缩Navier-Stokes方程组

流体是大自然中司空见惯的一种物质,如水,石油等,当然空气也可以看作一种特殊的流体.真空的含义是指在给定的空间内低于一个标准大气压的气体状态,是一种物理现象.在“虚空”中,声音因为没有介质而无法传播,但电磁波的传播却不受真空的影响.对于流体而言,一特定空间内部的部分物质被排出,使其压力小于一个标准大气压,则通称此空间为真空或真空状态.也可以简单表述为流体中有一部分的物质被排出,流体的密度在这个地方为零.对于流体力学方程,如Navier-Stokes方程组,欧拉方程组,若容许密度函数为零,研究在此种情形下流体的运动规律,特别是真空状态的变化情况而提出的问题,都可以称为真空问题.

真空的出现和消失都与Navier-Stokes方程组解的正则性相关.因此即便初边值中没有真空,一般情况高维可压缩Navier-Stokes方程组不能保证在有限的时间内不产生真空,只有在非真空附近小振荡时才有全局正则解.因此高维真空状态可否在有限的时间内形成是一个令人关注的问题.特别是,若初始密度包含一片真空时,由于在真空区域里无法定义流体的速度,此时在真空区域Navier-Stokes方程本身是否正确仍没有确定答案.事实上,对于一维粘性常系数的可压缩Navier-Stokes方程组的Cauchy问题,Ho ff和Smoller[1]证明了若初始不包含真空,以后也不会产生真空现象.David Ho ff和Denis Serre[2]证明了一维可压缩Navier-Stokes方程组物理弱解在真空区域收敛到一个非物理意义的弱解.此弱解表明,在真空出现时,一维可压缩Navier-Stokes方程组的物理解不必连续依赖于它们的初始数据.这些研究表明,真空问题有着独特的现象有待发现,而且此后我们认识到刻画真空状态从物理角度看最合理的模型是自由边值问题.此时,可压缩Navier-Stokes方程组具有如下特点:

(a)它是一个混合型方程组:双曲型方程和抛物型方程的耦合,而双曲型方程有很强的奇异性;

(b)密度函数为零时,方程组和边界条件都出现了退化现象;另外还可能存在密度集中的可能;

(c)方程里有若干复杂的非线性项,以及实际问题还可能涉及复杂的边界条件,这使得方程组有非常强的非线性性质.

正是上述种种困难,使得真空问题的研究具有极大的挑战性.在1980年Matsumura A.及其合作者关于初始远离真空的平衡态附近小扰动的可压缩Navier-Stokes方程组全局弱解存在性结果[3-4]得到以后,直到1998年才由Lions P.将其结果推广到可压缩Navier-Stokes方程组包含真空时的情形.他的结果容许初始密度有真空,初始动量和密度可以任意大.这是一个非常重要的结果,建立了一个全新的弱解存在性的证明框架,引起了广泛的关注.从此,一大批涉及真空的问题开始引起数学学家和物理学家的关注,真空问题的研究取得了一系列重要进展.

2 主要研究进展

正如上文所述,真空状态的存在带来了极大的研究困难,但其研究结果表明理论研究更加接近物理中流体运动的规律,蕴含了许多新的现象,也暴露了通常所采取的研究模型:粘性系数约定为常数的可压缩Navier-Stokes方程组有一定的局限性.

例如,Ho ffD.和Serre D.(见文献[2],一维)以及辛周平和袁洪君的结果(见文献[5],三维球对称)都揭示了若初始状态有真空,这个真空区域可以一直存在下去.这个结果与现实生活现象及物理观察不符.后来,利用修正的可压缩Navier-Stokes方程组,即粘性系数依赖于密度的可压缩Navier-Stokes方程组,辛周平,李海梁和李竞在文献[5]中证明了一维情形下这个初始真空状态一定会在有限时间内消失.对于初始没有真空的时候,Ho ff和Smoller在文献[1]证明了一维粘性常系数的可压缩Navier-Stokes方程组以后也不会产生真空现象.对于粘性系数依赖于密度的可压缩Navier-Stokes方程组,郭真华,李海梁和李自来在文献[7]中也证明了同样的结果.

因此,从实际研究结果看,流体粘性的作用不容忽视.但是在早期开展研究时,往往先从简单情形入手.下面将从粘性系数为常数以及粘性系数依赖于密度的可压缩Navier-Stokes方程组的真空问题这两个方面的研究出发,全面梳理真空问题的研究脉络,特别对粘性系数依赖于密度的可压缩Navier-Stokes方程组真空问题的相关研究作一个较为详细的介绍,希望能给读者关于真空问题的较为全面的了解.

2.1 粘性系数为常数的情形(即µ,λ为常数)

当粘性系数为常数时,关于Navier-Stokes方程组(7)解的全局存在性及长时间行为的研究已有大量文献.一维的结果已相当完善(参见文献[1,8-13]).关于高维等熵可压缩Navier-Stokes方程组(7),当初值不包含真空时,Itaya,Nash,Serrin和Tani在文献[14-17]证明了经典解局部适定性.当初始值在非真空常状态附近时,高维等熵可压缩Navier-Stokes方程组的经典解整体适定性也得到证明(参见文献[3-4,18-23]).

当初值包含真空时,为了克服退化引起的困难,韩国数学家Choe H.J.和Kim H.引进了一个相当巧妙的相容性条件(文献[24-29]),证明了经典解或强解的局部适定性.对于任意大初值,最主要突破由Lions[30]得到.当绝热系数时,Lions利用弱收敛的方法得到了弱解的整体存在性.接着,Feireisl,Novotny,Petzeltov在文献 [31-33]把 Lions的结果推广到.江松,张平在文献[34]中证明了球对称弱解的整体存在性(γ≥1).江松和张平[35],孙文俊,江松和郭真华[36]分别得到了轴对称和螺旋对称整体弱解的存在性.最近,在压力不是热力学稳定的和各向异性应力张量的条件下,Bresch和Jabin[37]利用紧性理论的方法得到了弱解的整体存在性.

Lions和Feireisl[30-33]的整体弱解最主要限制是初始总能量是有限的,因此,密度函数可以在无穷远处消失或密度函数有紧支集.而关于弱解的结构信息很少,特别地,整体弱解正则性及唯一性仍是一个公开问题.但是辛周平[38]证明了当初始密度函数有紧支集时,热传导系数为零的非等熵可压缩Navier-Stokes方程组Cauchy问题的任意属于空间

的经典解会在有限时间内爆破.其结果对等熵可压缩Navier-Stokes方程组成立.Rozanova[39]把文献[38]中初始密度函数有紧支集的假设推广到密度函数在无穷远处衰减比较快.最近,辛周平和闫伟[40]去掉了文献[38]中初始密度函数有紧支集和初始总能量有限的假设,即允许初始含有真空.然而辛周平和闫伟[40]的爆破结果并不适用于三维等熵可压缩Navier-Stokes方程组的Cauchy问题.当初始值包含真空,甚至有紧支集,黄祥娣,李竞和辛周平[41]在小能量假设下证明了三维经典解整体存在性与唯一性.随后,李竞和辛周平[42]把这一结果推广到二维Cauchy问题.

从以上数学结果来看,真空带来的退化和奇性给非线性偏微分方程理论提出了前所未有的挑战.从物理角度来讲,若没有外力作用,流体连接真空的自由边界如何运动?真空运动的机制亟待我们去探究.事实上,早在2000年,罗涛,辛周平和杨彤[43]以及Ho ff[44](2002年)给出了气体和真空之间的界面附近解的正则及渐近行为.对于粘性系数为常数的等熵可压缩Navier-Stokes方程组自由边值问题,此时自由边界也可能出现真空状态.Nishida和 Okada在文献[45-46]中证明了当一边界固定,另一边界连接到真空时,一维Navier-Stokes方程组弱解的整体存在性,但它们区域都不包含球心.Okada和Makino在文献[47]中对于球对称情形得到类似的结果.值得注意的是Okada和Makino[47]考虑的是外区域{r|1≤r≤a(t)}及退化边界条件ρ(a(t),t)=0.郭真华和李自来[48]在包含球心区域{r|0≤r≤a(t)}及跳跃边界条件假设下,证明了自由边值问题球对称弱解的整体存在性.

2.2 粘性系数依赖于密度的情形(即µ=µ(ρ),λ=λ(ρ))

粘性系数依赖于密度的明确提法始于刘太平,辛周平和杨彤的文章[49],这篇文章引起了广泛的关注,带动了一大批数学工作者开展有关流体真空问题的研究.

这里,首先解释一下等熵可压缩Navier-Stokes方程组(7)中粘性系数µ和λ依赖于密度ρ的原因.在气体动力学理论中,当从Boltzmann方程组通过Chapman-Enskog二阶展开导出Navier-Stokes方程组时(参见文献[50-51]),在推导过程中会发现其粘性系数和热传导系数都依赖于温度θ.

这里ai(i=1,2,3)为常数(参见文献 [50]).事实上,对于截断反作用力模型,如果分子势能为r−a(r是分子间的距离),则

即θ=AR−1ργ−1,从而粘性系数依赖于温度转化为粘性系数依赖于密度.

当研究初始密度含真空的问题时,由于粘性系数依赖密度的可压缩Navier-Stokes方程组在真空区域会出现粘性项消失引起方程组发生退化变型,这使得有关整体解的适定性,渐近性态等基础性问题的数学研究变得极其困难.另外在地球物理学中,研究流体运动时所用的很多数学模型是与粘性系数依赖于密度的Navier-Stokes方程组相似的.如在等熵可压缩 Navier-Stokes方程组(7)中取N=2,µ(ρ)=ρ,λ(ρ)=0和γ=2时,其结果正是浅水波的Saint-Venant系统.

下面,按照粘性系数µ和λ依赖于密度的不同情形分别予以介绍.

2.2.1 粘性系数µ为常数,λ依赖于密度(λ=λ(ρ))

粘性系数µ和λ中,仅λ依赖于密度函数的等熵可压缩 Navier-Stokes方程组(又称Kazhikhov-Vaigant模型)可以描述为:

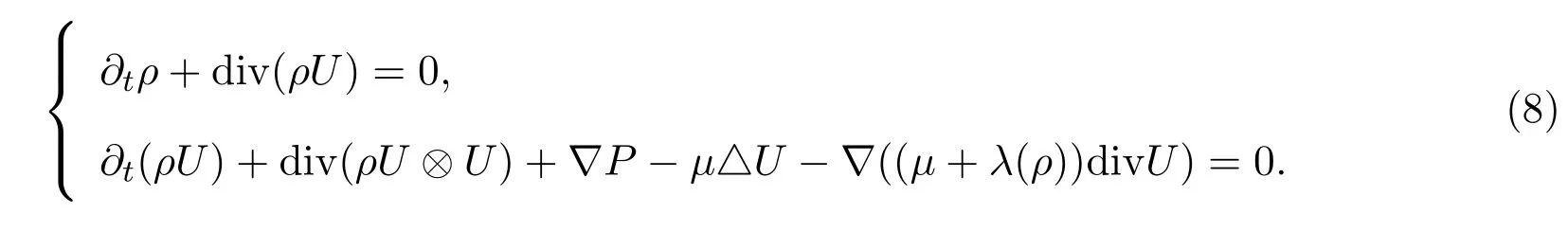
这里ρ和U=(u1,···,uN)分别表示流体的密度和速度,P=ργ(γ>1)为压强,µ为粘性系数,λ(ρ)=ρβ且满足

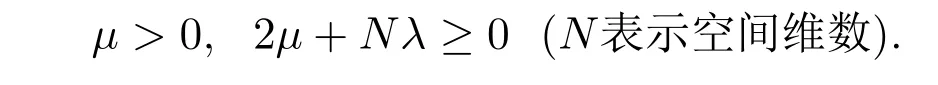
1995年,Vaigant和Kazhikhov[52]首次提出这一模型,所以又称之为Kazhikhov-Vaigant模型.当初值远离真空且β>3时在周期区域上证明了二维经典解的整体适定性[52].Perepelitsa[53]在β=γ>3时,证明了弱解的整体存在性及长时间行为.最近,对任意大且包含真空的初值,当β>3且满足相容性条件,酒全森,王益和辛周平[54]在二维周期区域上证明了经典解的整体适定性,这是模型(8)关于初值包含真空的第一个结果.之后,这一结果被黄祥娣和李竞[55]推广到情形.接着,在β>3条件下,酒全森,王益和辛周平[56]及黄祥娣和李竞[57]分别证明了对任意包含真空初值的二维Cauchy问题整体光滑解存在性和唯一性.粗略地说,文献[56]在速度上加权,而文献[57]则在密度上加权.之后,酒全森,王益和辛周平[58]把文献[56-57]的结果推广到初值不包含真空情形.Ducomet和Necasova[59]证明了二维初边值问题光滑解整体适定性,但这里不是一般的Dirichlet边界条件,而是涡度类型边界条件.而对于Kazhikhov-Vaigant模型在一般的Dirichlet边界条件下解的整体适定性仍是一个公开问题.

最近,李海梁,辛周平和张兴伟[60]在β>1条件下证明了二维球对称自由边值问题整体强解的存在性唯一性及长时间性态.由于模型(8)的粘性系数依赖于密度而导致的复杂的非线性结构,类似三维情形的结果仍是一个公开问题.于是,郭真华,王梅和王益[61]考虑了三维球对称Cauchy问题的弱解的整体存在性.后来,王梅,李自来和郭真华在文献[62]中还证明了三维自由边值问题在跳跃边界条件下球对称弱解的整体存在性.

2.2.2 粘性系数µ和λ均依赖于密度(即µ=µ(ρ),λ=λ(ρ))

假设流体具有有限质量,忽略外力和地球重力的影响,流体由于自身分子的作用,流体将会呈现一种自由流动的状态.此时,数学上我们将赋予方程组一个自由边值条件.按照流体在边界上是否包含真空状态,将自由边值条件分为两类:跳跃边界条件和连续边界条件.特别是连续边界条件,流体在边界上也出现退化,与初始真空带来的退化结合,给问题的研究带来非常大的困难.一维情形较为容易处理,结果比较完善.高维情形非常复杂,只有部分进展.这方面的研究一直方兴未艾.

下面从一维和高维两种情形分别予以说明.

(i)一维情形

(a)跳跃边界条件

一维粘性系数依赖于密度的等熵Navier-Stokes方程组的自由边值问题:

其中(ξ,τ)∈Ω={(ξ,τ)|a(τ)≤ξ≤b(τ),τ>0},且满足如下初值条件:

和边值条件

这里ρ,υ分别表示流体的密度和速度,P=P(ρ)为压强,µ(ρ)=ρθ为粘性系数.对于多方理想流体情形,即

这里a(τ),b(τ)为自由边界,定义如下:

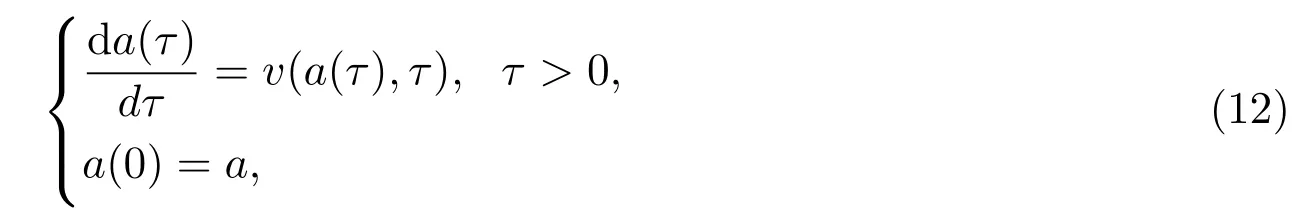
和

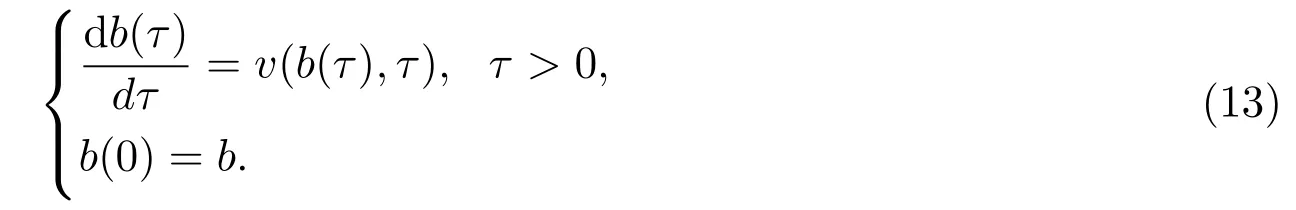
由质量守恒可得

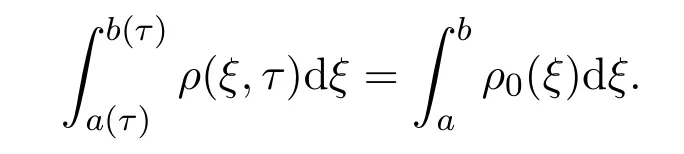
为了方便,通常假设

在Lagrange坐标下,处理自由边值问题更为方便.为此,引入Lagrange坐标变换

这把区域 [0,T]×[a(τ),b(τ)]变成 [0,T]×[a,b],且满足

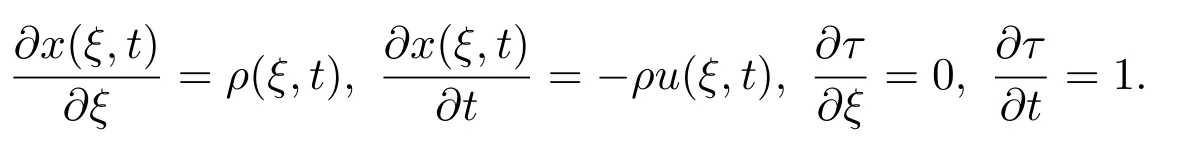
自由边值问题(1)-问题(3)变成

(x,t)∈[0,1]×[0,T],初边值条件变成

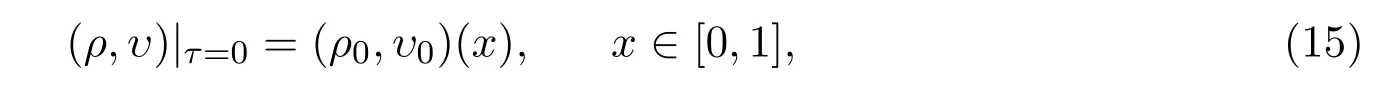
和

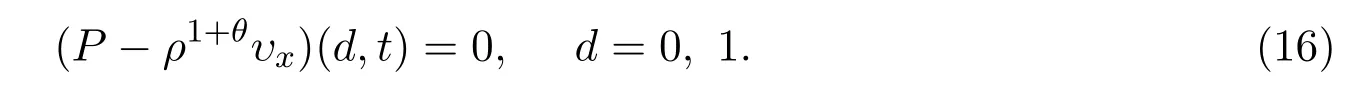
当粘性系数µ和λ依赖于密度时,由于粘性系数依赖密度的可压缩Navier-Stokes方程组在真空区域会出现粘性项消失引起方程组发生退化变型,这使得有关整体解的适定性,渐近性态等基础性问题的数学研究变得极其困难.考虑一维粘性流体流体在自由边界处跳跃连接真空且粘性系数µ=cρθ时,刘太平,辛周平和杨彤在文献 [49]和 Makino在文献 [63]中得到了Navier-stokes方程组弱解的局部存在性.Okada,MatuNeasov和Makino在文献[64]中,在的条件下用类似于文献[65]的方法证明了弱解的整体存在性和唯一性.紧接着,杨彤,姚正安和朱长江在文献[66]中得到条件下弱解的整体存在性.之后,这个结果被江松,辛周平和张平在文献[67]中推广到了0<θ<1的情形.秦绪龙,姚正安和赵会江在文献[68]中推广到0<θ≤1的情形.郭真华,江松和谢峰在文献[69]中推广到更一般情形

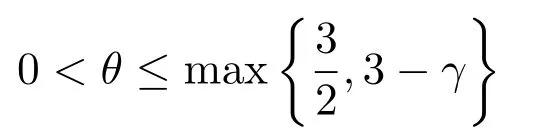
且γ>1.最后,朱长江[70]在θ>0的假设下第一个证明了密度函数关于时间的渐进行为和衰减率估计.

(b)退化边界条件

对于退化边界条件,即边界条件(16)变成如下边界条件:

关于初始密度连续连接到真空状态的自由边值问题,杨彤和赵会江[71]在

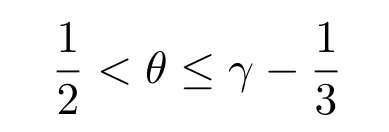
条件下,证明了弱解的局部存在性.杨彤和朱长江[72]得到了时弱解的整体存在性.之后,Vong,杨彤和朱长江[73]以及方道元和张挺[74]分别得到了0<θ<1/3和0<θ<1时弱解的整体存在性.郭真华,朱长江在文献[75]中推广到更一般情形

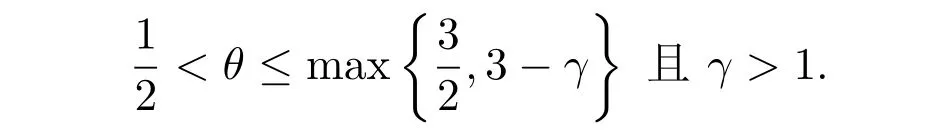
最后,郭真华和朱长江[76]在θ>0的假设下第一个证明了密度函数关于时间的渐进行为和衰减率估计.

(c)初边值条件

李海梁,李竟和辛周平在文献[6]中证明了当

时,在Dirichlet边界条件

和周期边界条件下,弱解的整体存在性以及对任意熵弱解,真空在有限时间内消失.

对于全空间三维球对称初值问题,方道元和张挺等[77-78]针对外力作用或与波松方程耦合时弱解的存在性及解的长时间行为展开了研究.

(ii)高维情形

在高维情形下，粘性系数依赖于密度时，有以下几个非常困难的问题:一是如何构造近似解.若保持熵估计的结构性条件,近似系统的设计非常重要.二是解的正则性提升问题.这里主要是真空奇性带来的挑战.三是紧性证明中真空状态的运动规律.最近,李竞和辛周平在文献[79]中对上述问题给出了一个完美的答案.

下面对高维研究进展作一个简要介绍.

(a)高维问题研究概述

高维粘性系数依赖于密度等熵可压缩Navier-Stokes方程组

其中

或者

如果µ(ρ),λ(ρ)满足

第一个结果是 Bresch,Desjardins和 Lin[80]对 Korteweg系统(带有 Korteweg压力张量κρ∇△ρ)证明了弱解的L1稳定性.之后,Bresch和Desjardins[81]将这一结果推广到消失毛细血管项(κ=0)但增加了二次摩擦项rρ|U|U.由于Bresch,Desjardins和Lin的BD熵不等式提高了密度函数正则性,Mellet和Vasseur[82]利用控制ρu2的L∞(0,T;LlogL(Ω))型不等式证明了可压缩Navier-Stokes方程组弱解的L1稳定性.把文献[80-81]相应的L1稳定性结果推广到

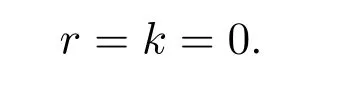
然而,虽然L1稳定性是证明弱解存在性最重要一步,但Korteweg系统和高维粘性依赖与密度的Navier-Stokes方程组弱解存在性仍是一个公开问题.其主要困难在于怎么构造满足L1稳定性的逼近解,使之满足L1稳定性所需要的能量估计、BD熵不等式、Mellet-Vasseur型不等式.由于粘性系数在真空上的退化性和构造的逼近解必须满足熵不等式,这样似乎是很困难的.值得指出的是Bresch和Desjardins在文献[83]中构造了二维带有毛细血管项浅水波方程组逼近解,并且证明了全局弱解的存在性,但是他们构造逼近解的方法对没有毛细血管项模型及高维粘性依赖与密度的Navier-Stokes方程组并不适用.郭真华,酒全森和辛周平在文献[84]中利用Bresch,Desjardins和Lin的BD熵不等式研究了有界区域上的粘性系数依赖于密度且满足(21)的三维可压缩Navier-Stokes方程组的球对称弱解的存在性,这是关于高维粘性系数依赖于密度的可压缩Navier-Stokes方程组弱解整体存在性的第一个结果.随后,郭真华,李海梁和辛周平在文献[85]中进一步研究了具有间断边值条件的粘性系数依赖于密度的高维等熵可压缩Navier-Stokes方程组的自由边值问题的球对称弱解的存在性和解的长时间行为,证明了它同样具有拉格朗日结构,内部正则性和边界正则性.同时,郭真华和辛周平在文献[86]中对于退化和跳跃两类边界分别构造了几类特殊形式的解析解.最近,李竞和辛周平[79]在

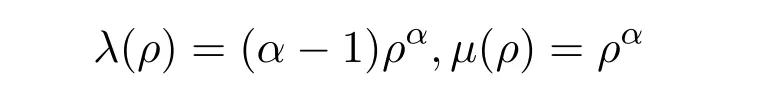
下,证明了粘性系数依赖于密度的等熵可压缩Navier-Stokes方程组在二维周期区域T2和全空间R2或者三维周期区域T3和全空间R3弱解的整体存在性.Vasseur和俞成[87]在二维周期区域T2和三维周期区域T3,粘性系数满足

三维粘性系数依赖于密度的等熵可压缩Navier-Stokes方程组弱解的整体存在性.

对于高维粘性系数依赖于密度的等熵可压缩Navier-Stokes方程组(7),这里的粘性系数

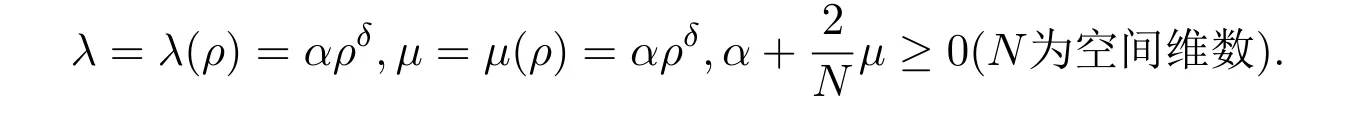
当δ=1,初始密度在无穷远处为真空时,李亚纯,潘荣华和朱圣国[88](朱圣国[89])证明了二(三)维经典正则解的局部适定性.当1<δ时,李亚纯,潘荣华和朱圣国[90]证明了三维经典正则解的局部适定性,最近当1<δ时,辛周平和朱圣国[91]证明了三维正则经典解的整体适定性.当0<δ<1时,辛周平和朱圣国[92]证明了三维经典正则解的局部适定性.而对于当0<δ<1时,三维经典正则解的整体适定性仍有待解决.

(b)物理真空现象的研究

对于自由边值问题的边界条件可以分为跳跃边界条件和连续边界条件,而对于连续边界条件又可分为光滑连续到真空和Hlder连续到真空.物理真空是引力场作用到运动的流体上时在边界上形成的真空状态,这时自由边值问题的边界条件为Hölder连续连接到真空.即,声速

在真空边界是C1/2-Hölder连续的.换句话说,物理真空主要是由场引起的,但数学上,有无场的存在,这类真空边界总是存在的.当然,物理真空可以通过不同的物理系统(例如,带阻尼的 Euler方程组,Euler-Poisson方程组和液化星球的 Navier-Stokes-Poisson方程组)的自相似解和稳态解来了解.物理真空(粘性流体和真空的界面)模型可以用下述的可压缩Navier-Stokes-Poisson方程组的真空自由边值问题来刻画:

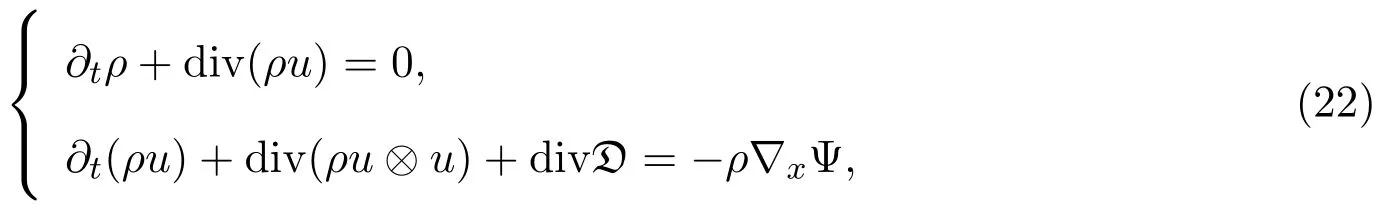
其中ρ和u分别表示密度和速度,D和ψ应力张量和重力势能,具有如下形式:

和

这里G为重力常数,I3为3×3单位矩阵,p为压强,µ为剪切粘性系数,λ为体积粘性系数.

由于声速在真空边界附近的强退化性,得到可压缩Navier-Stokes-Poisson方程组的真空自由边值问题解的高阶偏导数的正则性是一难题.当粘性系数为常数和粘性系数依赖于密度时,Jang[93]和段琴[94]证明了可压缩Navier-Stokes-Poisson方程组(22)的真空自由边值问题强解局部适定性.在物理学中,最重要的是证明解的整体高阶正则性以便更深刻地认识解的大时间性态.罗涛,辛周平和曾慧慧[95]证明了当时粘性液体星球Lane-Emden解的非线性渐进稳定性.同时,罗涛,辛周平和曾慧慧[96]考虑了当时粘性系数依赖于密度的粘性液体星球Lane-Emden解的非线性渐进稳定性.相比张挺和方道远[77]的结果,这一结果适用更广的粘性系数形式.Jang和Tice[97]证明了当时粘性液体星球Lane-Emden解的非线性渐进不稳定性.文献[98]研究了Lane-Emden解的线性稳定性.

很显然,除去上述结果外,物理真空问题提出了许许多多的研究课题有待我们去解决.

3 公开问题

∗毫无疑义,Lions P.文中的弱解在含有真空时的唯一和正则性是一个令人关注的重要问题！这个问题即使对定常情形也都是公开的！

∗真空的出现和消失都与Navier-Stokes方程组解的正则性相关.因此,即使初边值中没有真空,一般情况下真空问题的研究都不可避免,只有小振荡时才有全局正则解.因此高维真空可否在有限时间形成是一个公开问题.

∗关于李竞和辛周平[79]及Vasseur和俞成[87]的整体弱解的正则性和唯一性一直没有得到解决.一方面,无论在文献[79]还是在文献[87]中，证明弱解整体存在性时,都需要粘性系数满足特殊关系式(λ(ρ)=ρµ′(ρ)−µ(ρ))以保证 BD 熵不等式成立.对于任意粘性系数,粘性系数不满足上述特殊关系式,等熵可压缩Navier-Stokes方程组弱解的整体存在性是一个公开问题.另一方面,对于高维粘性系数依赖于密度的等熵可压缩Navier-Stokes方程组(7),当粘性系数为

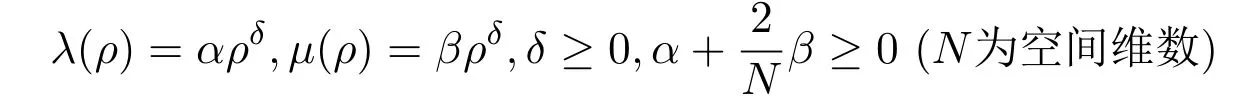
形式时,由于可以包含浅水波模型(λ(ρ)=µ(ρ)=ρ),无论是否有小性要求(如初始能量小,或在某个平衡态的小扰动等),因其研究具有重要的物理应用前景而令人关注.相关问题,譬如经典解的整体存在性问题,解的长时间行为等,也引起了大家的研究兴趣.

∗对于粘性系数依赖于温度的非等熵可压缩Navier-Stokes方程组的研究,除了一些小性假设结果[99-100],其他结果很少,毫无疑问这个问题的研究将面临一个巨大的挑战.