基于细胞神经网络图像去噪算法研究

（新疆财经大学应用数学学院，乌鲁木齐市，830012） 王丽娟 李国东

图像恢复的一个重要方面是图像去噪。图像恢复是一门快速发展的学科，目前在许多领域得到广泛应用[1]。一方面，图像已经成为生理学，心理学和计算机科学视觉感知的有效工具;另一方面，图像处理在科学研究，医疗保健，工业生产，通信，管理和教育等方面也起着非常重要的作用。随着多媒体技术的飞速发展，人类生活与图像之间的关系更加紧密，另外，计算机科学技术的飞速发展，为图像处理的快速发展奠定了基础，并使图像处理技术不断向前发展。在图像传输，采集和存储过程中，往往会受到各种噪声的干扰和影响，从而降低图像质量，图像处理算法直接关系到后续图像处理的效果，如分割图像，识别目标，边缘提取等等，因此获得更高质量的图像，对图像进行降噪处理是必要的，既尽可能地保持原始信息的完整性，又能够去除无用信号中的信息。因此，去噪一直是图像修复的核心。

噪声在图像处理中是一个非常重要的问题。对给定图像的改进是图像去噪的最终目标。在各种图像系统中，由于图像转换和传输期间的噪声干扰而导致图像质量下降[2]。在当今的大多数应用中，需要高质量，高清晰度的图像。因此，提高图像质量和抑制噪声的研究具有重要意义。在图像处理领域，图像去噪一直是最基础，最重要的研究内容之一，具有非常重要的现实意义和理论价值。

1 图像噪声

理论上，噪声被定义为一个不可预测的随机误差，只能通过概率方法来理解[3]。因此，图像噪声可以视为一个多维随机过程，它是由一个随机过程描述的，即概率密度分布函数和概率分布函数。但在大多数情况下，这种描述方法更加复杂，甚至难以完成。在实际应用过程中，通常用数字特征来描述，即均值方差，相关函数等。这些数字特性在一定程度上反映了噪声的特性。

噪音是导致图像退化的重要因素之一。今天的数字图像系统使用输入图像来冻结然后将图像从多维信号转换为一维图像。图像的多变换处理构成多维图像信号，并且通过相同的方法分解和合成相同的图像噪声。图像传感器在工作期间容易受到各种因素的影响，例如图像采集中的环境条件和传感器组件本身的质量。对于不同类型的图像噪声，人们对图像的感知程度并不相同，这是人们通常所说的噪声视觉特征[4]。

1.1 常见的图像噪声

噪声会影响图像的信号和相位，有些噪声与图像信号无关，有些与噪声有关。

1.1.1 高斯噪声

高斯噪声是一种概率密度函数服从高斯分布（正态分布）的噪声，是一种加性噪声[5]。加性噪声与图像信号的强度没有相关性，并与信号相加。无论信号是否存在，噪声都会存在，即将噪声直接添加到原始图像中。

可以表示为：

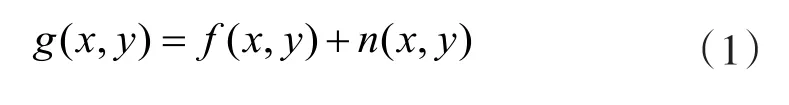
上式中，g(x,y)为加入噪声的图像，f(x,y)为原始图像，n(x,y)代表噪声。

1.1.2 椒盐噪声

椒盐噪声主要是由传输通道，图像传感器等产生的黑白相互交错的噪声[6]。椒盐噪声通常是由图像切割造成的。

1.1.3 乘性噪声

乘性噪声是因为在传输过程中信道引起的。与信号是相乘的关系，若信号存在噪声就存在，反之，不存在。

可以表示为：

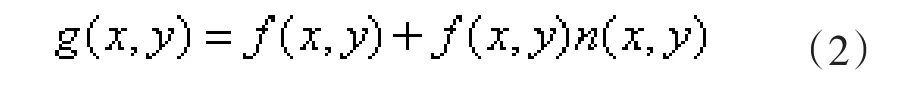
上式中，g(x,y)为加入噪声的图像，f(x,y)为原始图像，n(x,y)代表噪声。

2 3阶细胞神经网络图像去噪算法

2.1 细胞神经网络

细胞神经网络[7（]CNN）由Berkeley大学的L.O.Chua和L.Yang于1988年提出。它是一个由大量细胞组成的非线性局部连接神经网络。当每个胞元连接到其邻近的8个胞元时，每个胞元记作c(i,j),(i,j=1,2,3,…)，并且连接的强度由模板的参数值决定。

设一个整体的区域范围，细胞以r为半径，并且所有细胞满足，

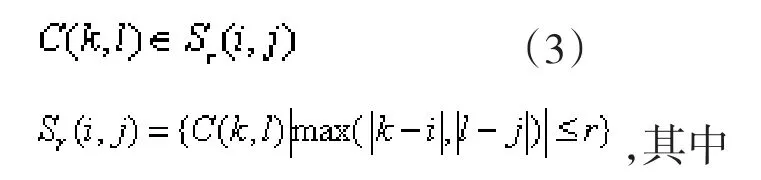
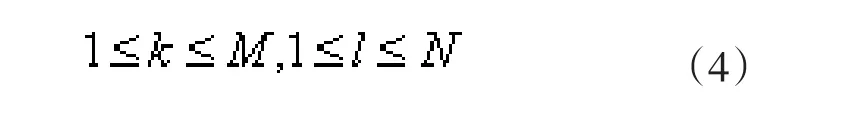
其中，r 表示细胞的邻域半径；C(k,l)表示细胞； C(i,j)的r邻域内的细胞。

细胞神经网络的表示方法如下：

细胞c(i,j)的状态方程为：

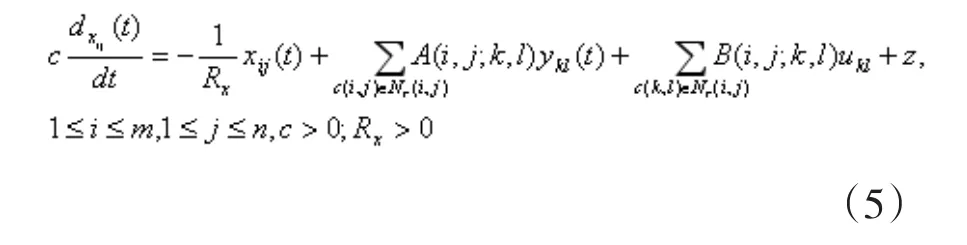
输出方程：

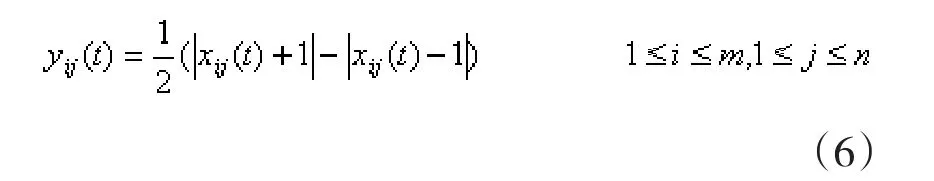
输入方程：

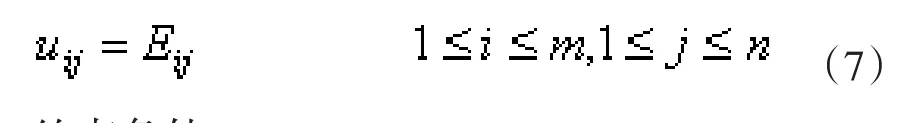
约束条件：

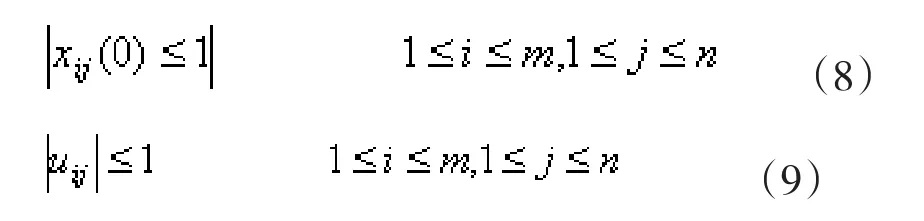
对称性：

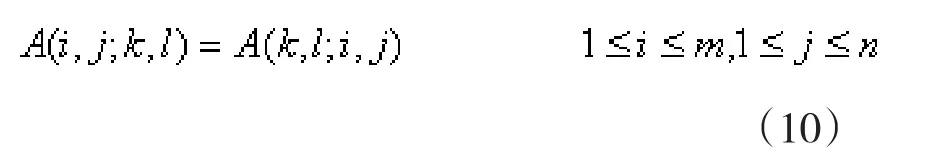
由（5）式得出CNN胞元的输入由参数 B(i,j;k,l)决定，输出由参数 A(i,j;k,l )决定。故由 A(i,j;k,l )与B(i,j;k,l)确定的矩阵A与B分别被称为反馈模板和控制模板。输入、状态与输出的关系完全由反馈模板A、控制模板B和阂值z来确定。通过选择最佳参数确定细胞之间的连接强度。

2.2 3阶细胞神经网络图像去噪算法

图像的降质退化模型可以用矩阵向量形式描述为

式中，g 是退化图像，f 是原始图像，n是噪声，H代表原始图像与退化图像关系的矩阵。

式中， 为复原图像，λ是正则化参数。

CNN的能量函数：

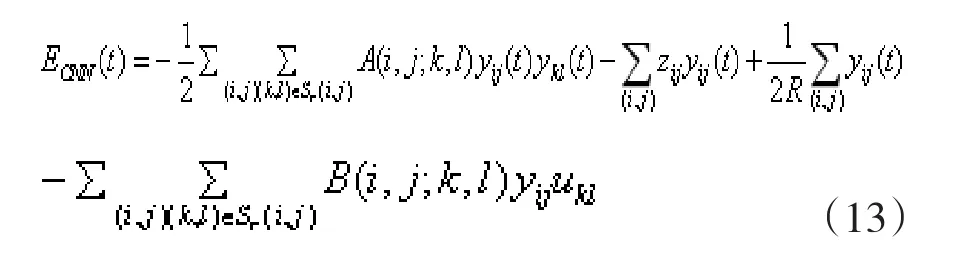
该能量函数随时间的变化：

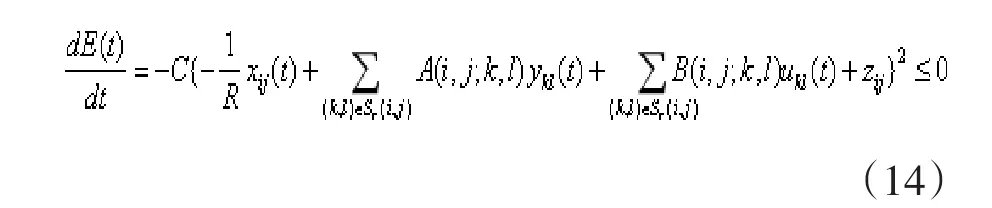
当CNN用于图像恢复时，数组的大小与恢复的图像大小相同。在恢复中，噪声图像首先被映射为CNN的初始值到CNN的空间排列的细胞阵列上；然后使用CNN搜索网络能量，以使CNN达到稳定的平衡点。这种稳定的平衡是CNN的最低能量函数，也是正则化最小点的方程。此时CNN输出的是满足（12）式约束最优解，即图像复原的结果[8-11]。主要问题是如何将方程（12）的系数映射到CNN的能量函数中，最终得到一组满足条件的模板。

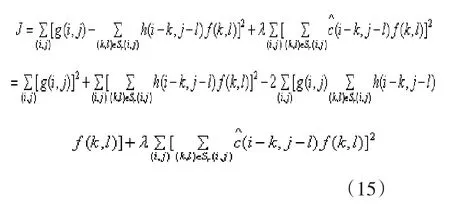
若令

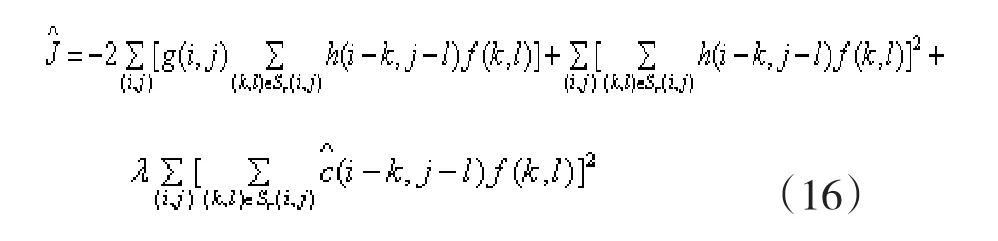
那么

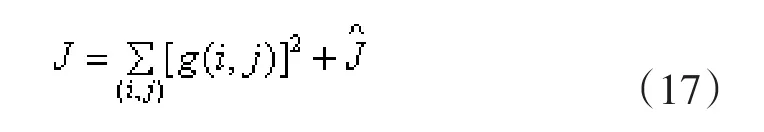
把展开，可以写成以下形式：

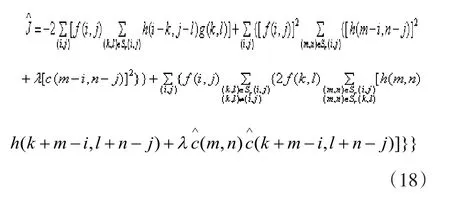
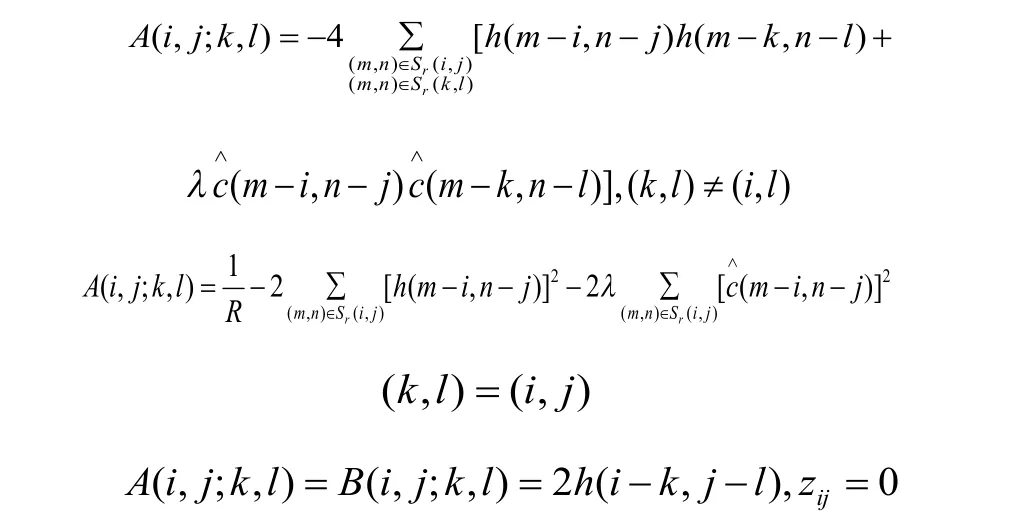
可以取模板为：

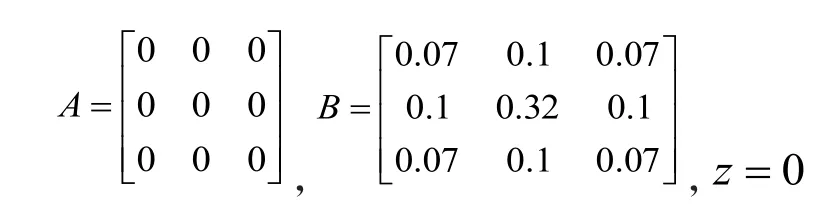
3 仿真及结果分析

采用matlab软件，对255*255原始图像加入1%的噪声，分别用3阶CNN、中值滤波、均值滤波的方法对同一幅含噪图像进行处理。为了验证图像恢复的效果，本文使用峰值信噪比（PSNR）、均方误差（MSE）作为评估指标。PSNR是“Peak Signal to Noise Ratio”的缩写，一般用于最大值信号和背景噪音之间。通常图像经过去噪后，输出的图像都会与原始图像不一。为了衡量经过处理后的图像质量，通常采用PSNR值来认定。一般PSNR值越大，图像失真越小，即去噪效果越好。计算公式如下：

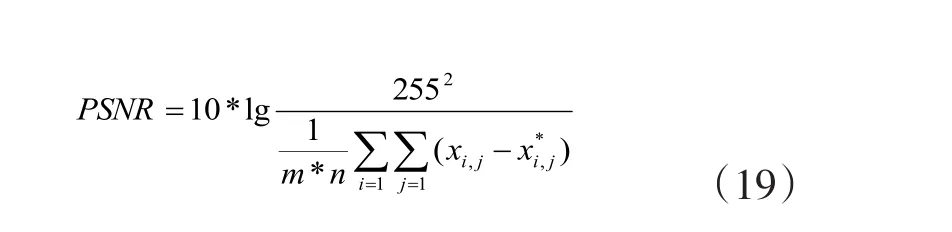
式中，x 为原始图像，x*为去噪后的图像，m,n分别为图像的行和列。均方误差法首先计算原始图像和还原图像像素差值的均方值，然后通过均方值大小来确定还原图像的失真度。计算公式如下：

表1 实验结果对比

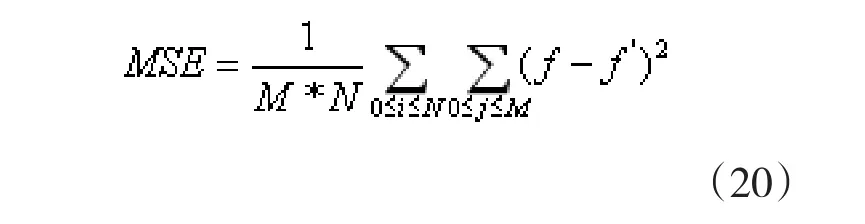
其中，M、N 为图像的长和宽，f为原始图像的像素值，f'为去噪后还原图像的像素值。

由表1可知，3阶细胞神经网络（CNN）方法的峰值信噪比（PSNR）大于均值滤波、中值滤波的PSNR，且3阶细胞神经网络（CNN）去噪方法的均方误差（MSE）相比均值滤波、中值滤波的小。从而可知，3阶细胞神经网络（CNN）去噪效果优于中值滤波、均值滤波去噪效果。