基于Actor-Critic强化学习的倒立摆智能控制方法

邱宇宸

(南京市第二十九中学，江苏 南京 210036)

自从Deepmind推出的智能围棋手击败人类围棋专业选手李世石后，强化学习理论引起全世界人工智能学者的关注[1]。强化学习是一种有别于监督学习和非监督学习的一种智能学习方法，亦叫弱监督学习[2-4]。该方法主要基于马尔科夫随机过程的基础上，基于环境的稀疏反馈(奖励)学习到期望的动作准则[5]。强化学习的方法，目前被广泛用于离散系统的优化控制，如机器人路径探索与规划，以及设计复杂游戏自动玩家[3,4]。显然，这些都是未知建模或是不可建模的动态。

倒立摆作为经典的机器系统，是测试和验证控制算法及理论的代表性设备[6-9]。实际上，在倒立摆模型物理信息明确的情况下，传统的控制方法已经得到非常理想的控制效果。但如果其模型信息未知，比如摆的质量、初始化状态等，传统的控制理论可能无法奏效。本文将提出一种基于Actor-Critic强化学习的倒立摆智能控制方法，为模型不确定的机器设备的控制提供参考方案。

一、倒立摆物理模型

图1 倒立摆模型示意图

在忽略空气助力的情况下，倒立摆系统的动力学模型可表示为：

(1)

(2)

以上两个式子中，变量的物理意义分别为：M：小车质量，m：摆杆质量，b：小车摩擦系数，l：摆杆长度，I：摆杆惯量， ：摆杆与垂直向上方向的夹角。其中，(1)式是小车水平受力平衡得到，(2)式则是通过摆杆的力学平衡建立。

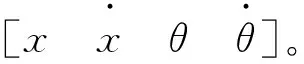
二、Actor-Critic算法原理

Actor-Critic算法原理的结构如图2所示。在理论上，Actor-Critic算法是强化学习算法的一种，主要是针对符合马尔科夫过程设计。算法工作流程如下：(1)策略网络Actor根据环境状态输出动作；(2)环境根据动作更新状态并给出奖励；(3)评价网络Critic根据环境状态和Actor输出的动作进行评价；(4)根据Critic的评价，策略网络Actor调整自身的动作策略(5)评价网络Critic则根据奖励值更新评价准则。循环执行该过程，直到两个网络收敛。图中的TD error意为前后两次采样时间评价网络的打分的差值[5]。通过TD error来训练强化学习模型的方法实现学习机的单步更新，缩短了训练的时间[6]。

图2 Actor-Critic算法原理图

本质上，策略网络Actor和评价网络Critic可分别理解为解析式未知的动作函数和值函数，因此可以采用神经网络的方法对这两个函数进行学习逼近。当网络收敛时，即学到了相应函数的“黑盒”表达。文中策略网络Actor和评价网络Critic分别由两个RBF神经网络构成。

RBF神经网络是仿生学、应用数学结合的产物[10-12]，也是目前主流的人工智能算法之一。通过非线性映射及加权组合，RBF神经网络能以任意精度逼近任意连续函数[13,14]。其结构实际为三层前向网络，如图3所示。

图3 RBF神经网络结构图

设网络的输入向量为x，输出向量为y,则网络的映射关系可表示为：

y=θTφ(x)

(3)

其中φ(x)为输入的2阶范数的径向基函数值，φ(x)=[φ1,φ2,…,φn],对于每个有：

(4)

式中，b表示径向基函数的宽度，c表示函数的中心。此外，θ=[θ1,θ2,…,θn]为权向量。在训练过程中，RBF神经网络的性能指标函数取：

(5)

其中yd(t)为期望输出。

根据BP训练算法，网络参数的更新公式如下：

θj(t)=θj(t-1)+η(yd(t)-

y(t) )φj+α(θj(t-1)-θj(t-2) )

(6)

(7)

bj(t)=bj(t-1)+ηΔbj(t)+

α(bj(t-1)-bj(t-2))

(8)

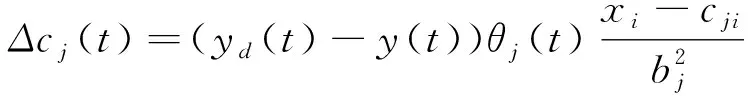
(9)

cji(t)=cji(t-1)+ηΔcji(t)+

α(cji(t-1)-cji(t-2))

(10)

三、实验与分析

所提出的算法将通过MATLAB平台进行仿真实验。倒立摆物理模型则依照第三节的模型公式通过欧拉公式进行差分建模，采样时间为0.01秒。倒立摆的模型参数为：M= 1.0kg，m=0.1kg，b=0.0005，l=0.5m，I= 1kg·m2。摆杆的初始偏角为小于2.5°的随机值，小车的初始位移为0。小车的最大移动位移为2.4m，摆杆的最大摆角为15°。

在控制算法上，Actor网络和Critic网络的学习率均为0.25，动量因子均为0.1。Actor网络为4-6-1结构，Critic网络为5-6-1结构。环境的奖励模式为：当小车超出最大位移或是摆杆超过最大角度时，奖励为-1；否则奖励为0。当控制器使倒立摆系统保持5000个采样周期不倒，则认为算法训练成功。

仿真实验结果图4-7所示。从四个实验可以看出，所提出的算法能在有限的尝试次数内学习到保持倒立摆平衡的方法。从各个图的控制曲线上看，最初都存在震荡，但最终都会趋于收敛，使得摆杆偏角为0且小车的位移为0，证明了所设计算法的有效性和可行性。

图4 第一次实验(第198次尝试达到目的)

图5 第二次实验(第150次尝试达到目的)

图6 第三次实验(第184次尝试达到目的)

图7 第四次实验(第50次尝试达到目的)