基于纠缠度条件下猎鹿量子博弈模型的纳什均衡分析

朱蒙爱，吴 茜，张新立

近年来，国内外学者从不同角度，对猎鹿博弈进行了分析，并取得显著成果.Z W Sun研究了量子策略解决困境的条件，得出了一般量子博弈合作演化的条件［1］；Tsubasa Ichikawa在猎鹿博弈中提出施密特分解的量子新方法，得出相位结构可以对纠缠进行更系统的分析［2］；V Sasidevan和Sitabhra Sinha利用动态系统观点来研究双人博弈，得到纳什均衡和合作均衡之间的差异［3］；Tsubasa Ichikawa和Izumi Tsutsui在对偶映射中讨论相位结构，得出基于量子博弈所获得的相位结构可以解决猎鹿博弈的困境［4］；Maciej-Kos研究了参与人在一次重复猎鹿博弈中的行为与风险态度之间的关系，得到第一轮的行为不能用任何常用的风险诱导工具来解释［5］；Azhar Iqbal建立概率框架，得出不可分解的EPR联合概率会改变猎鹿博弈的纳什均衡，他还将演化博弈论和量子博弈论展开联系［6］.

综上，不难看出，国内外学者大部分都是讨论相位结构和联合概率对纳什均衡解的影响，而利用Marinatto和Weber的量子化方案对猎鹿博弈模型进行量子化处理的甚少，基于此，本文以MW量子方案为基础，对猎鹿博弈进行量子化研究，分析纠缠度对纳什均衡解造成的影响，得到纠缠度可以为我们解决经典博弈中遇到的困境，即量子方案为我们提供了解决困境的新方法.

1 经典猎鹿博弈纳什均衡解分析

猎鹿博弈主要内容是两个人出去打猎，猎物为鹿和兔，他们互不知道对方选择的猎物.如果一人选择鹿，则需要另一人也选择鹿，产生合作才能成功狩猎.而选择兔为猎物，不需要合作，即：背叛也能成功狩猎，但是猎兔的收益要小于猎鹿的收益.该博弈的收益矩阵如表1所示，表中第一个值为参与人Alice的收益，第二个值为参与人Bob的收益.

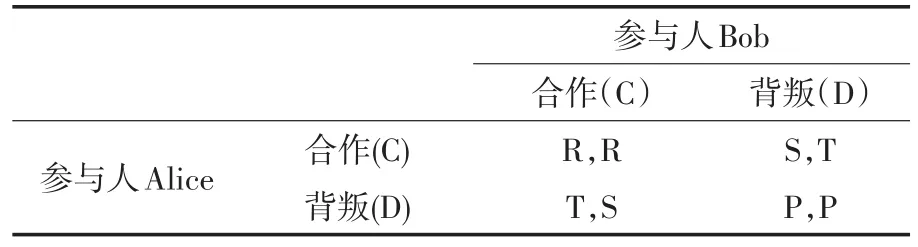
表1 猎鹿博弈收益矩阵表

其中各收益参数之间存在R＞T≥P＞S的关系.以下为了讨论方便，假定收益参数分别选取R=4，T=3，P=3，S=1等数值.根据纳什均衡定义可知，猎鹿博弈一共存在三种纳什均衡.纯策略纳什均衡为（C,C）或(D,D)，混合策略纳什均衡为(C ,C )，其中混合策略意味着当Alice有的概率选择合作时，就有的概率选择背叛，Bob亦如此.虽然经典猎鹿博弈中，对整体有利的策略（C,C）是帕累托最优，亦是个体理性的最终选择，但存在着一定的风险，因为一旦Bob选择策略D，选择策略C的Alice将获得最低收益，所以是选择冒险取得最优收益，还是选择稳定收益，两个参与人都陷入了困境.

2 量子猎鹿博弈模型建立

猎鹿博弈模型建立的具体步骤如下：

第1步：博弈是在二维的希尔伯特空间进行，参与人各拥有两个量子比特，且构成一个量

第4步：由于该博弈的两个策略分别为合作(C)和背叛(D)，那么双方的支付算子就为：

第5步：博弈双方的最终收益为：

博弈的具体过程如图1所示.

图1MW量子博弈方案

3 量子猎鹿博弈模型的纳什均衡解分析

根据MW量子博弈方案，初始纠缠量子态为

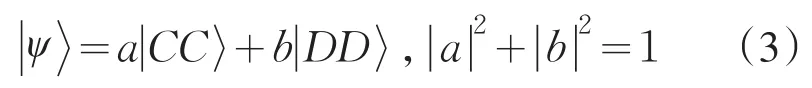
该量子态适用于一般的双人博弈，并且这种形式的初始量子态具有直接引入纠缠，参数少，还能将实数与复数联系在一起等优势，其中θ是纠缠参数，θ的取值范围是.根据（1）和（2）式，参与人的收益计算成如下形式$A(p,q)=

根据纳什均衡的定义，若(p*,q*)为纳什均衡，需满足条件$A(p*,q*)-$A(p,q*)=(p*-

计算可知，前两种纳什均衡的结果是独立于参数θ的，第三种纳什均衡是与参数θ相关的，时 ，满 足 $A,B(1,1)＞$A,B(0,0)＞的情况，即理性参与人会更倾向于选择收益更高的NE(1,1)，但是并没有解决困境，当博弈处于最大纠缠θ=时，满的情况，这与量子性别战中结果相同，即参与人明确知道对初始态实施操作存在导致(1,0)或(0,1)的风险，于是都选择不对初始态操作的战略，故而得到唯一的纳什均衡(1,1).因此猎鹿博弈在量子最大纠缠下，可以解决困境.

现在对上述分析结果，使用MATLAB R2015a作数值模拟，进行直观展示，三种纳什均衡对应的具体收益如图2所示.

图2 量子猎鹿博弈收益

4 结论

本文在经典和量子的视角下分析了双人猎鹿博弈的纳什均衡解，通过研究和计算发现，猎鹿博弈在经典博弈和量子博弈中都存在三种纳什均衡，并且纠缠程度θ与纳什均衡解的选择有着密切的联系，当θ=0时，量子博弈会再现经典博弈中出现的情况，验证了经典博弈是量子博弈的子集；当，即最大纠缠时，会出现唯一的纳什均衡解，故而猎鹿博弈在最大量子纠缠下可以解决困境.在未来的科研工作中，是否可以将演化博弈论与量子博弈论结合，讨论量子纳什均衡解的稳定性？这有待于我们进一步研究.