教材习题开发利用的策略

陈卫青

【摘   要】教材习题不仅包含着基础知识与基本技能，还蕴含着解题策略、数学思想和方法等内容。要发挥好教材习题的练习作用，就需要教师对教材习题进行深入的分析，充分挖掘隐藏在这些习题中的资源。具体操作可以从以下四方面着手，对教材习题进行开发利用：借题发挥;举一反三;领会题意;改编习题。

【关键词】习题;数学教学;策略

教材习题内容丰富，图文并茂，不仅包含着基础知识与基本技能，还蕴含着解题策略、数学思想和方法等。笔者通过“教材练习素材的利用与开发”这一课题，对课后习题进行了深入的分析，边教学边实践，很好地发挥了习题的练习作用。现对实践中所运用的几点策略总结如下，供大家教学时参考。

一、借题发挥，突出方法与规律的提炼

教材在编写课后习题时，除了紧扣本节课的知识与技能，还会安排一些具有代表性的素材，使学生练习后能更好地总结方法、提炼规律。

比如在教学人教版五年级下册“最大公因数”后，教材配有以下习题。

找出下面每组数的最大公因数。

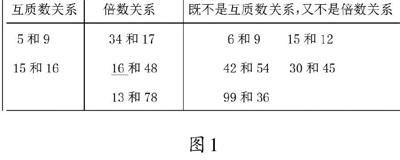
6和9    15和12    42和54    30和45    99和36

5和9    34和17    16和48    15和16    13和78

教材对这10组数做了精心的设计。这10组数中有两个数是互质数关系的若干组，两个数是倍数关系的若干组，两个数既不是互质数关系又不是倍数关系的若干组。如果教师在教学时，只让学生求出每组数的最大公因数，而不引导学生针对各组数的特点进行方法和规律的提炼，那只能是单一的训练。所以教师有必要在学生找出每组数的最大公因数后，提出以下问题：怎样能更快地找到两个数的最大公因数？

学生针对这一问题先独立思考，分小组讨论后，教师再组织集体交流。

生：我看到这10组数中有两个数是倍数关系的，小的那个数就是这两个数的最大公因数。

师：你能举例说明吗？

生：如“13和78”，这里的78是13的6倍，13就是78的因数，所以13和78的最大公因数就是13。

师：以上10组数中两个数是倍数关系的还有吗？（教师根据学生的回答，重新把有倍数关系的组写在一起）

生：如果两个数的公因数只有1，那最大的公因数就是1。如“5和9”，最大公因数是1。

师：很好！两个数的公因数只有1，我们把这两个数叫作互质数。

生：我发现两个数是相邻的自然数时，这两个数的最大公因数也是1。如“15和16”这两个数的最大公因数是1。

师：是吗？大家是否再举例说一说？（学生说了很多，如16与17，17与18，288和289……这样的两个数的最大公因数都是1）

师：除了两个数是互质数关系、倍数关系的，还有什么关系？

根据学生的回答，教师作如下板书（如图1）。

图1

师：当两个数既不是互质数关系，又不是倍数关系时，用什么方法能更快地找到最大公因数？

生：在两个数中，先把小的数的因数都找出来，再看看哪个因数是大的数的因数，找出最大的因数就是这两个数的最大公因数。如“6和9”，6的因数有1，2，3，6，发现3是9的因数，所以“6和9”的最大公因数是3。

师：你们再想想，有必要把较小数的因数都找出来吗？

生：可以把较小的数除以2来比较。如“6和9”，把6除以2等于3，这3又是9的因数，所以“6和9”的最大公因数就是3。如“15和12”，把12除以2等于6，6不是15的因数，再把6除以2等于3，这3是15的因数，所以“15和12”的最大公因数就是3。

师：好！大家用这种方法再找一找另外3组数的最大公因数，看是否可行？（过程略）

师：这种方法叫作把较小数缩倍法，但一定都要除以2吗？如碰到“27和36”，只要把较小的数27除以3等于9，9是36的因數，也就找到“27和36”的最大公因数是9。

接着教师借以上分析又向学生提出以下的练习：

①如果“a和36”的最大公因数是12，且a<36，那a是（         ）。

②如果“a和36”的最大公因数是1，且a<36，那a是（         ）。

生：第①题a=12，24;第②题a=1，5，7，11，13，17，19，23，25，29，31，35。

教材习题解答后，教师继续向学生提出问题，引导学生进一步概括解题的方法和规律，并利用发现的规律提出新的练习。这样的延伸性提问和补充，能把原题的功能发挥得淋漓尽致。

二、举一反三，突出解题思路的拓展

由于受版面的限制，教材中同一内容、同一性质的练习材料相对较少。而学生在学习过程中不可能只通过一两个练习就能进行归纳、提炼，所以需要教师根据教材提供的练习材料，自主创编出适量的、具有相互关联的习题，可采用“一题多问，一题多解，一题多变”等方式，触类旁通，拓宽学生解题的思路。

（一）一题多问，加深理解解题方法

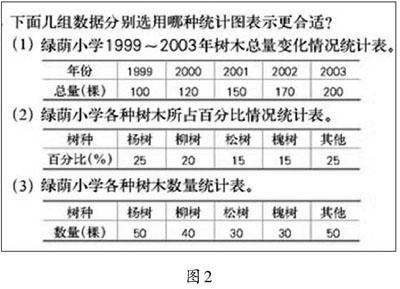
“一题多问”，不是每一题都要去“多问”，有些题不需要多问，有些题自然要多问。比如老版（2009年3月第2版）的人教版教材六年级上册“扇形统计图”中有这样一道练习题（如图2）。

图2

此题的练习目的是“能根据具体数据选择合适的统计图”。教学时，教师往往希望学生回答出预设答案：第（1）组数据更适合画折线统计图;第（2）组数据更适合画扇形统计图;第（3）组数据更适合画条形统计图。接着教师最多会追问：为什么？

这样的教学，此题的功能没有得到应有的发挥。教师可在学生回答说理后，继续补充以下问题。

问题1：请你们想一想，根据第（2）组数据绘制成的扇形统计图会是什么样子的？

在学生比画表述后，教师再出示一组图，向学生提出：你想象的统计图的样子应该是哪个图？

问题2：下面是绿荫小学去年种下各种树木成活率统计表（如图3），你觉得根据表中的数据可以画出扇形统计图吗？

图3

大部分学生回答：可以。沉默片刻后就有越来越多的学生发现，这张表格中的百分数表示的是各种树木的成活率，相互没有关联，所以不能画成扇形统计图。

问题3：题目中第（2）组数据中的百分数是怎样计算出来的？

学生通过观察回答：第（2）组数据中的百分数是根据第（3）组数据算出来的。

这时教师让学生根据第（3）组数据算一算是不是刚好是第（2）组数据中的百分数。然后出示图4，再向学生提出要求：请你根据表中的数据画出扇形统计图。

图4

教材提供的三组数据，只要求学生选用画哪种统计图更合适。停留在这样的分析上，只能达到让学生认识各种统计图在什么情况下更合适的目的。如果以此题为背景，采用一题多问的方式，可使学生对扇形统计图有进一步的认知。

新版（2014年3月第1版）的人教版教材对此题作了极大的改进，在加深学生对解题方法的理解上有了很好的引领。

（二）一题多解，交流拓展解题思路

教材中有许多习题本身蕴含一题多解的特点，所以在学生解答后，教师要继续引导学生用多种方法去解答，并及时组织学生交流，使学生能更好地拓宽解题思路，提高解决问题的能力。

比如人教版五年级上册“多边形的面积”中有这样一题（如图5）。

图5

教师先让学生独立解题，并要求用不同的方法进行解答，接着展示学生的解题方法，最后进行分类整理并归纳解题思路。

第一类：先分割，再计算。

方法1：按上、下分（见图6-①），把阴影分割成上、下两部分，阴影部分的面积是：5×4÷2+（2+5）×4÷2=10+14=24（cm2）。

方法2：按左、右分（见图6-②），把阴影分割成左边是一个直角梯形，右边是一个钝角三角形。阴影部分的面积是：（4+5）×2÷2+5×6÷2=9+15=24（cm2）。

方法3：连对角线（见图6-③），分成两个钝角三角形，阴影部分的面积是：4×8÷2+2×8÷2=16+8=24（cm2）。

图6

第二类：先补充，再计算。

方法4：把它补成一个梯形（见图7-①），算式是：（4+8）×8÷2-8×6÷2=48-24=24（cm2）。

方法5：把它补成一个梯形（见图7-②），算式是：（2+8）×8÷2-8×4÷2=40-16=24（cm2）。

方法6：把它补成一个正方形（见图7-③），算式是：8×8-8×4÷2-8×6÷2=64-16-24=24（cm2）。

图7

第三类：直接数方格。

“一题多解”可培养学生的求异思维，促使学生从不同角度分析问题、解决问题，努力拓宽思维的广度。但在“一题多解”中，应注重学生在求异中的归纳、优化，使求异更有价值。

（三）一题多变，完善解题模式

一题多变是训练学生完善解题模式，提高思维灵活性的有效方法。如人教版六年级上册“分数除法”中有这样一道题。

挖一条水渠，王伯伯每天挖整条水渠的[120]，李叔叔每天挖整条水渠的[130]。两人合作，几天能挖完？

此题是已知工作效率的工程问题，可以直接运用的数量关系是“总工作量÷工作效率和=合作工作时间”，即“1÷（[120]+[130]）=合作工作时间”。基于此题的解题模式，可先回归到两人独做需要的工作时间上，并以此题变换出不同背景下的题目，如以下题组。

①挖一条水渠，王伯伯单独挖，需要20天完成;李叔叔单独挖，需要30天完成。两人合作，几天能挖完？

②从甲城到乙城，客车需要20小时，货车需要30小时;现在客车和货车分别从甲、乙两城同时相向开出，几小时后两车相遇？

③姐妹两人绕着周长为600米的池塘走路，姐姐单独走一圈要20分钟，妹妹单独走一圈要30分钟。现在她俩从同一地点同时相背出发，经过几分钟后两人相遇？

④一批木料，如果做课桌，可以做20张;如果做椅子，可以做30把。如果一张课桌配一把椅子为一套，这些木料可以做多少套这样的课桌椅？

⑤一个游泳池有两根进水管，单开甲管，20小时可以把空池注满;单开乙管，30小时可以把空池注满。现在同时打开甲、乙两管，几小时可以注满这个游泳池？

以上5题可使学生认识到只是问题背景在变，解题模式都是一样的。为防止学生产生思维定式，可再增加以下题目：

橘子成熟了，李叔叔说：我家果园里的橘子我一人采摘需要20天完成。王叔叔说：我家果园里的橘子我一人采摘需要30天完成。如果两人合作，几天可以摘完橘子？

三、领会题意，做好渗透

教材中的有些习题，蕴含着后继要学的数学知识，这就需要教师给予挖掘强化。如果及时引导学生进行延伸性思考，就能很好地激发学生对数学的学习兴趣，更好地渗透后继知识的学习。如人教版四年级上册“角的度量”这一单元，教材设计了多个图形的测量，都可渗透后继知识的学习。

如图8-①，此题让学生测量后去发现“对顶角相等”。

①                           ②                              ③

圖8

又如图8-②题，此题让学生发现“两条平行线之间所画的角的度数是另外两个角的度数的和”。

再如图8-③题，此题让学生发现“同弧所对的圆周角的度数相等”。

虽然这些知识要到中学才学习，但学生通过测量，不仅可巩固量角技能，更能感受到数学的奥秘。因此在教学这些习题时，除了完成原题的任务外，还应该进一步引发学生去举例验证，如图8-①，学生在发现对顶角相等后，教师可让学生在纸上任意画出两条相交的直线，去测量验证。

四、改编习题，提升价值

教材中的有些习题往往只针对某一知识点或某一技能，为了发挥习题的最大作用，在实际教学时，可根据学习内容和学生的实际情况，对习题进行改编。比如人教版四年级上册“认识平行四边形”做一做中有这样一题（见图9）。

图9

此题的意图是让学生发现所摆的平行四边形的形状有不同，从中认识平行四边形的不稳定性。笔者认为此题只给学生4根小棒，学生在拼摆时，只要把对边摆相等了，平行四边形也就摆成了。这样的题目思维含量低。为此，笔者在教学时将此题改编成了以下的问题（如图10）。

图10

从7根吸管中选择4根串成平行四边形，学生在解决这个问题时，要根据平行四边形的特征来思考。当选好4根吸管串成平行四边形时，这实际上做了一个能抽拉的学具，学生自然就认识到平行四边形具有不稳定性。

当学生选择2号管2根与3号管2根，串成平行四边形时，学生在抽拉中还认识到长方形是特殊的平行四边形。

当学生选择2号管4根，串成平行四边形时，学生在抽拉中除了认识到有四条边相等的特殊平行四边形外，还动态地认识到正方形是特殊的平行四边形。同时教师还可以告诉学生这四条边相等的平行四边形，还有一个名字叫菱形。

这样的改编，使学生动态地获得了平行四边形具有不稳定性，长方形、正方形都是特殊的平行四边形等知识，提升了习题的价值。

教材习题的开发利用，还有很多策略可以研究。

（浙江省临海市哲商现代实验小学   317000）