基于加权云模型的全电子联锁系统运营安全风险评估

孙 歌，陈光武，王诗豪

(1.兰州交通大学自动控制研究所，兰州 730070；2.兰州交通大学甘肃省高原交通信息及控制重点实验室，兰州 730070)

全电子化计算机联锁是我国轨道交通信号控制领域的新技术，其运用了计算机技术、网络通信技术、电力电子控制技术等，系统综合性强、结构与功能复杂、软硬件集成度高，其复杂性与传统计算机联锁系统相比具有更加严苛的安全需求[1]。

全电子化计算机联锁系统由全电子执行机、监测机、联锁机3部分组成。其中，全电子执行机代替传统计算机联锁系统中的继电器执行电路，完成联锁命令的执行及信息采集；监测机代替传统的微机监测设备，对整个系统的运行情况进行实时监测并记录；联锁机用以完成联锁逻辑运算，对信号设备状态的采集与控制，它们之间通过工业控制总线相互通信，实现控制、执行、监测一体化[2]。根据系统各部分所能实现功能的不同，全电子化计算机联锁系统的结构示意如图1所示。

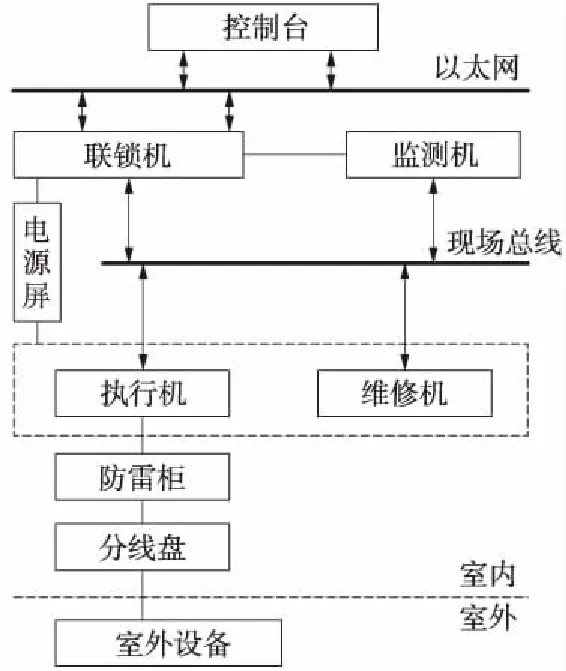
图1 全电子化计算机联锁结构示意

我国铁路行业的安全风险评估体系，主要由以结合我国铁路实际情况推出的铁路应用EN5012X系列标准和IEEE Std 1474.1—1474.4/IEEE Std 1483等标准为依据，以专家评估法、故障树分析法、事件树分析法等定性、定量分析法为基础组成的[3-6]。国内部分学者的研究情况有：文献[3-4]通过构建多级可拓模型对系统进行定量分析；文献[5]提出建立灰色模糊评估模型，对系统安全性进行分析；文献[6]采用模糊预测控制理论，对有轨电车ATP系统进行分析。上述文献主要通过模糊数学或复杂网络的方法对于复杂系统进行分析，但计算过程中需要大量的失效率和故障概率等较难准确获得的数据，且结果并不能直观反映出风险的严重等级。文献[7]试将云模型引入系统安全风险评估中，但在评估过程中只通过风险概率确定风险等级是不全面的。另外，在权重的确定上多采取单一的主观赋权或客观赋权[7]，已有学者试采用组合赋权，但在权重的组合上采用了乘法组合，这样的组合方式反而会增大计算误差，使得大数相乘得大，小数相乘更小。

为解决上述问题，引入最优组合赋权法计算权重，使之既能反映主观评价者的信息，又具有原始数据的客观性。最后采用云模型来实现定性概念与其定量数值之间的不确定信息转换，分别构建风险严重度模型和风险可能性模型，最终通过两种模型与风险矩阵相结合确定系统的安全风险容忍等级。

1 安全风险评估方法介绍

1.1 安全风险评估基本概念

目前对轨道交通信号系统安全风险评估方法的研究，往往局限于通过故障概率对系统进行安全评价，而对系统安全风险评估方面的研究较少。安全风险评估的目的是明确所有危险源，确定系统安全风险状况，使系统能够持续的识别、评价及控制其安全风险[8]。

安全风险是对危险源后果的一种度量方法，用数学公式可表示为：安全风险度(risk)=风险可能性(likelihood)×风险严重度(severity)，即单个危险源的风险度等于该风险源发生的可能性与后果严重程度的乘积。将风险可能性和风险严重度分别分为5个等级，即可得到安全风险评估矩阵，如表1所示。

表1 安全风险评估矩阵

根据安全风险评估矩阵，可得出以下安全风险容忍等级：风险评估指数为[20，25]，风险容忍度为Ⅰ级，即不可容忍；风险评估指数为[12，20)，风险容忍度为Ⅱ级，即不期望；风险评估指数为[6，12)，风险容忍度为Ⅲ级，即可接受；风险评估指数为[1，6)，风险容忍度为Ⅳ级，即可忽略。

1.2 云模型理论

云模型是一种实现定性概念与定量数值间不确定信息转换的工具，能够在较高层次中划分并泛化属性值，并能模拟人类的思维方式，很好地处理具有随机性和不确定性的数据[9-10]。可将云模型引入到系统安全风险评估中来，弱化由于计算机系统的行为产生的随机和不确定性因素。

用来表征云的3个数字特征为：期望、熵、超熵。

期望(Ex)是云滴在评估区间中分布的期望，是定性概念定量表示的中心点。

熵(En)是定性概念的不确定性度量，由定性概念的随机性和模糊性共同决定。并能反映两者的关联性。

超熵(He)是熵的不确定性的度量，即熵的熵，它能够反映云滴的离散程度，并间接地反映云的厚度，即超熵越大，云的厚度越大。

3个数字特征的值不同，云的形状也不同，如图2所示，图2(a)与图(b)分别表示了熵和超熵的不同对于云模型离散程度的影响。

图2 云模型数字特征关系示意

1.3 最优组合赋权

权重的确定可分为主观法和客观法两种。主观法是人为主观地对各属性进行赋权，主要有专家确定法、评分法、层次分析法等；客观法是根据数据信息确定权重的方法，最常用的是熵值法[11-13]。主观赋权过于依赖专家的主观评价和经验知识，客观赋权又缺少经验支撑，都具有局限性。为减小主观随意性同时又能兼顾客观数据包含的信息，本文引入了一种最优组合赋权的方法，使得到的评估结果能够准确、合理地反映客观事实。

假设某一多指标综合评价问题，对n项指标由m种赋权方法对其赋值，其中第k种赋权方法给出的权重向量值为

Wk=(w1k，w2k，…，wnk)，k=1，2，…，m

(1)

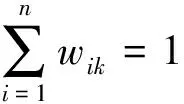
则m种赋权方法的集成权重表示为

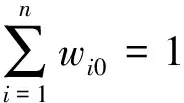
(2)

则第j项指标的组合权重可以表示为

(3)

μt为第t种赋权法的权重系数。为此，只要求出权重系数μt，就可以代入求出指标的组合权重。

权重系数μt在组合权重中的意义是使指标评价值能够尽可能地分散，充分体现出不同被评指标间的差异。所以，权重系数的求取可以最小方差原理构建最优化模型，即集成权重W0与已知权重Wk的偏差Δ=W0-Wk最小，其中k=1，2，…，m。最优化模型为

(4)

将上式进行化简，得

(5)

随后，根据矩阵的微分性质，写出上式最优化解的一阶导数条件为

(6)

对应的线性方程组

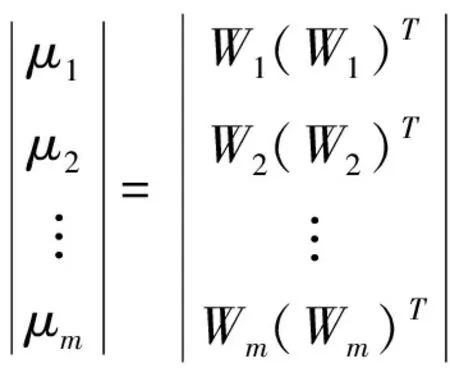
(7)

求解方程组可得到μ1，μ2，…，μm的解，进而求出各个指标的最优组合权重。权重系数的求取在系统安全风险评估中尤为重要，其合理与否直接影响到评估结果。通过最优组合法计算出的指标权重可以克服单一赋权法的片面性，既能弱化系统评价的主观性，又能涵盖多方面评价信息，是一种权重计算的新的合理、准确的方法。

2 最优组合赋权下的云模型安全风险评估过程

2.1 建立全电子化计算机联锁系统运营安全评估指标体系

系统安全评估体系是在影响系统安全的各种因素综合考虑的基础上建立的，从软硬件设备、人员、环境、管理、维修5个方面出发，依据客观全面、合理可行的原则建立全电子化计算机联锁系统安全评估指标体系[14-16]，如图3所示。

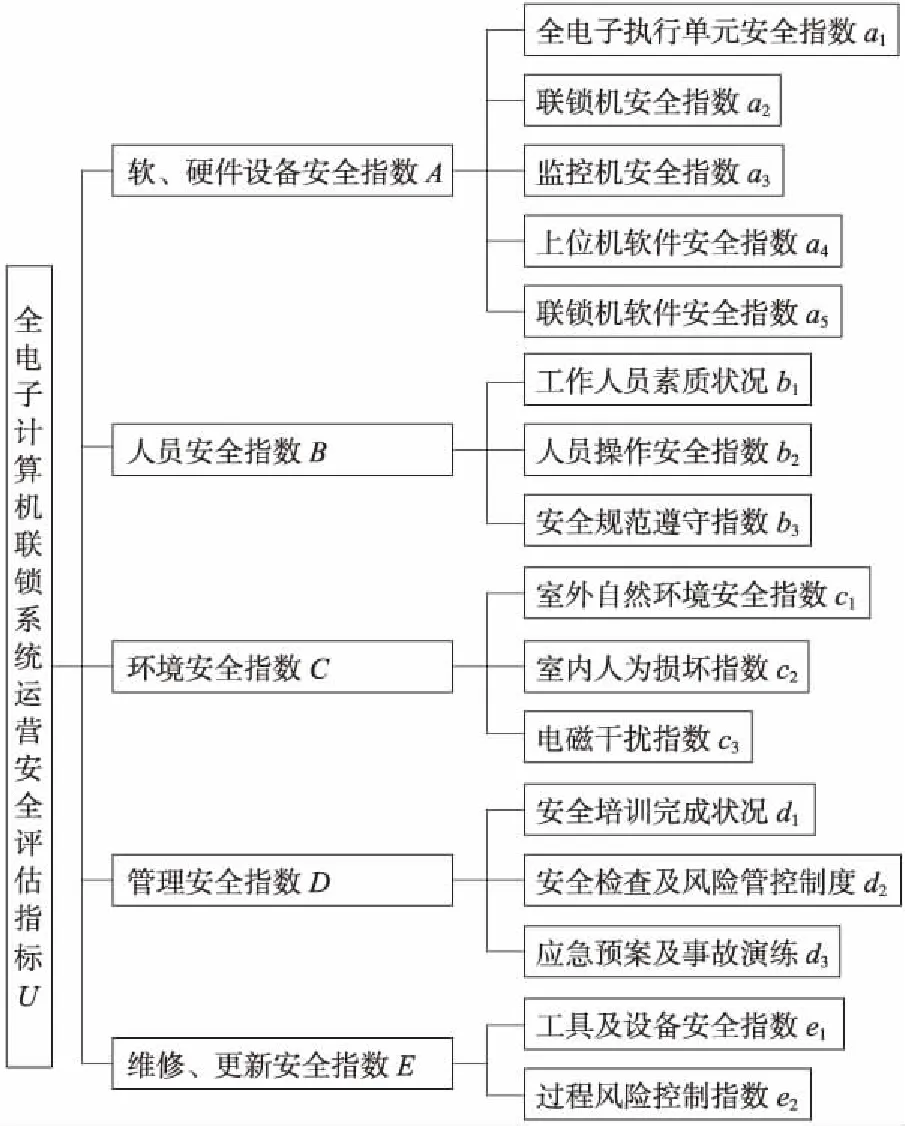
图3 全电子化计算机联锁系统安全评估指标体系

2.2 建立评估标准云

根据安全风险评估等级，利用正向云发生器，生成全电子化计算机联锁系统风险可能性评估标准云和风险严重度评估标准云[17]。假设评估值取值范围为[0，100]，为方便计算将该区间等分为5个子区间，分别是：[0，15)可忽略的(不太可能)[15，35)轻微的(极少)；[35，65)严重的(偶尔)；[65，85)特别严重的(经常)；[85，100]灾难性的(特别频繁)。每个子区间对应一个标准云Ci(Exi，Eni，Hei)，其中i=1，2，…，5。

假设区间的限值为Rimax、Rimin，其中i=1，2，…，n，则参考文献[7，19]的计算方法，期望可表示为

(8)

根据式(8)的结果计算熵

(9)

Hei=η，η为常数。经验取η=1，可以计算出评估标准云为

C1(0，5，1);C2(25，6.67，1);C3(50，10，1);C4(75，6.67，1);C5(100，5，1)。

由此生成的评估标准云如图4所示。

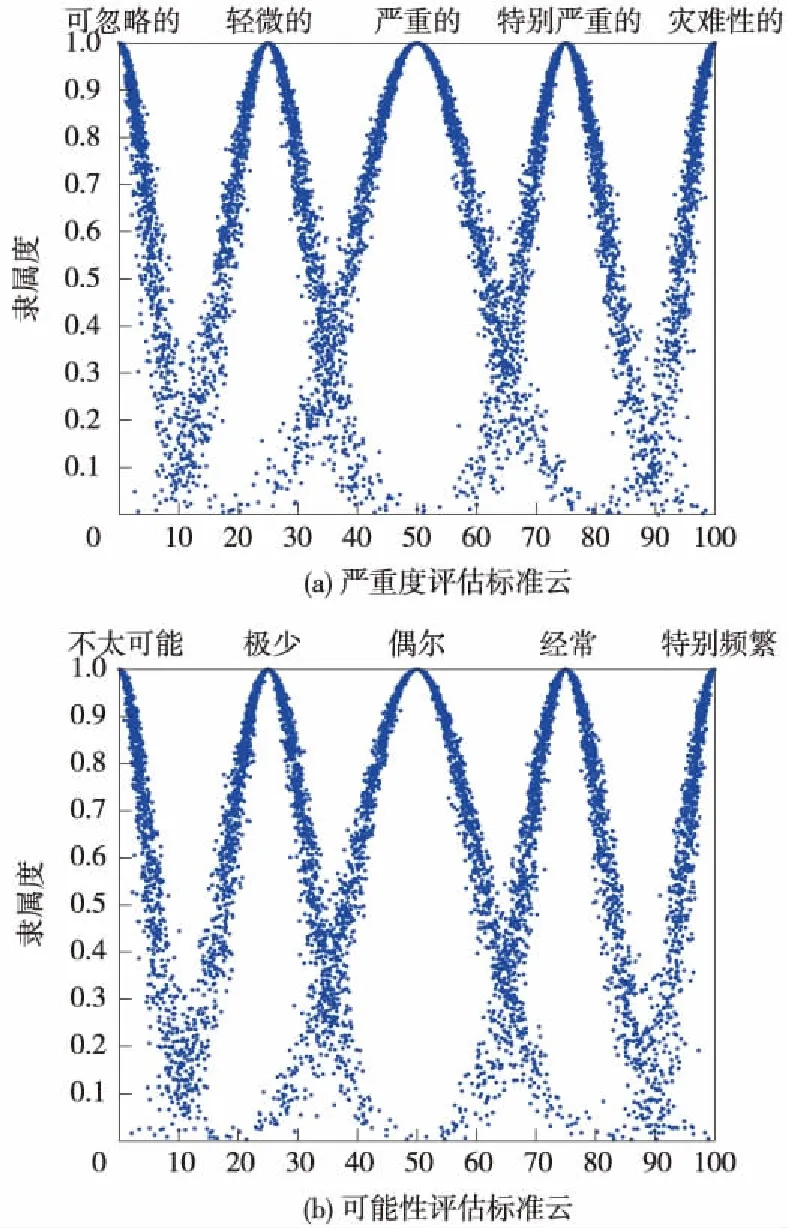
图4 评估标准云模型

2.3 建立综合评估云

邀请n位专家对评估体系的16个底层指标(a1…a5，b1…b3，c1…c3，d1…d3)，e1，(e2)进行打分，对打分结果进行处理，求出风险可能性熵权和风险严重度熵权。并将权重的计算结果代入云计算，分层计算得到可能性综合评估云CS=(ExS，EnS，HeS)和严重度综合评估云CP(ExP，EnP，HeP)。综合评估云的数字特征计算方法如下。

(1)计算期望

(10)

(11)

(2)计算熵

(12)

(13)

(3)计算超熵

(14)

(15)

其中Δ为方差。

同理可得CP的数字特征

(16)

(17)

(18)

2.4 确定风险等级

根据得到的严重度综合评估云和可能性综合评估云，分别得出系统严重度等级和可能性等级，对比表1便可得到系统的安全评估等级。

3 分析验证

以全电子化计算机联锁系统为例，验证算法的可行性及有效性。

3.1 数据处理

根据图2可得，目标层指标集U包含5个指标，底层指标集包含16个指标。由于计算复杂，本节的权重确定都通过软件Matlab7.0编程计算。

第一步 邀请专家对底层指标集

A={a1，a2，…，a5};B={b1，b2，b3};

C={c1，c2，c3};D={d1，d2，d3};

E={e1，e2}

风险严重度和风险可能性进行量化评估，再依据专家打分对照风险等级得出风险赋值表。打分采用百分制，100分表示风险等级最高，0分表示风险等级最低。

第二步 确定客观权重

风险严重度赋值如表2所示。

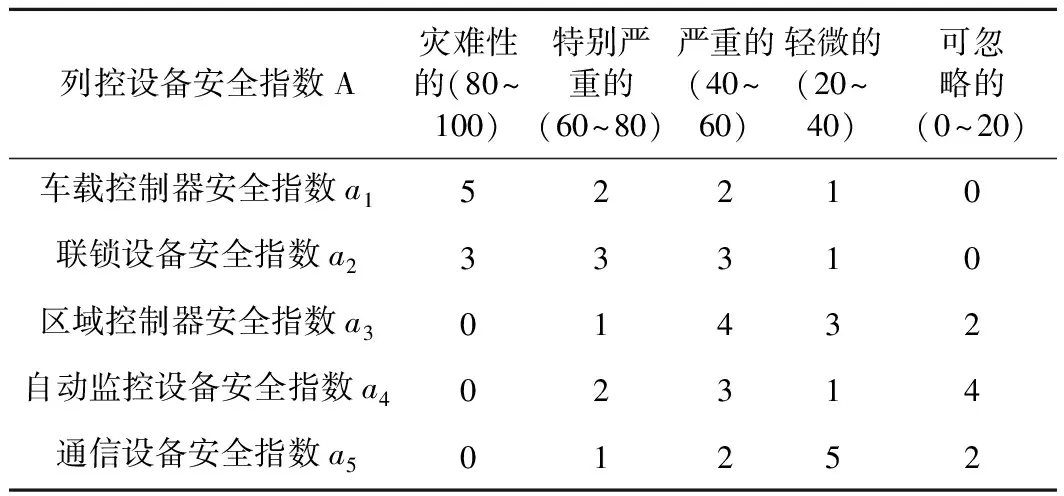
表2 风险严重度赋值

根据指标A风险严重度赋值表可以写出指标A的风险严重度判别矩阵

由此可得指标A的风险严重度客观权重

同理可得目标层其余指标的严重度客观权重为

则层次总排序后的严重度权重向量为

0.032 0，0.042 5，0.097 1，0.057 8，0.170 8，0.144 1，

0.069 2，0.038 4，0.109 8，0.034 9)

第三步 确定主观权重

通过对指标严重度的两两比较构造判别矩阵

计算出风险严重度主观权重

0.044 5，0.039 9，0.182 9，0.069 8，0.013 4，

0.007 1，0.037 9，0.004 4，0.020 1，0.007 7，

0.082 7，0.020 7)

第四步 最优组合赋权确定指标权重

权重系数的求取在系统安全风险评估中尤为重要，其合理与否直接影响到评估结果。本文采用熵权法和层次分析法分别确定指标的客观权重和主观权重，即m=2，则(7)式可表示为

0.039 5，0.017 1，0.025 7，0.106 9，0.109 5，

0.056 5，0.054 1，0.031 8，0.102 5，0.072 3，

0.044 0，0.022 6，0.095 9，0.027 6)

同理可求出风险可能性权重

WP=(0.027 7，0.067 8，0.082 6，0.202 4，

0.046 7，0.100 3，0.035 1，0.024 0，0.045 2，

0.020 9，0.014 4，0.018 5，0.030 3，0.015 9，

0.206 6，0.061 4)

通过最优组合法计算出的指标权重，可以克服单一赋权法的片面性，既能弱化系统评价的主观性，又能涵盖多方面评价信息。

3.2 生成评估云

以底层指标a2发生故障，即系统执行单元与联锁机通信故障为例[20]。10位专家对指标的打分评语集为风险严重度评语集

Sa1={85，82，76，78，83，88，76，79，80，77}

风险可能性评语集

Pa1={35，38，26，20，29，40，23，35，42，38}

其余指标中各底层指标评分同法可得，由于篇幅原因不再一一列出。

根据式(10)、式(12)、式(14)计算出底层指标严重度评估云的3个数字特征，如表3所示。

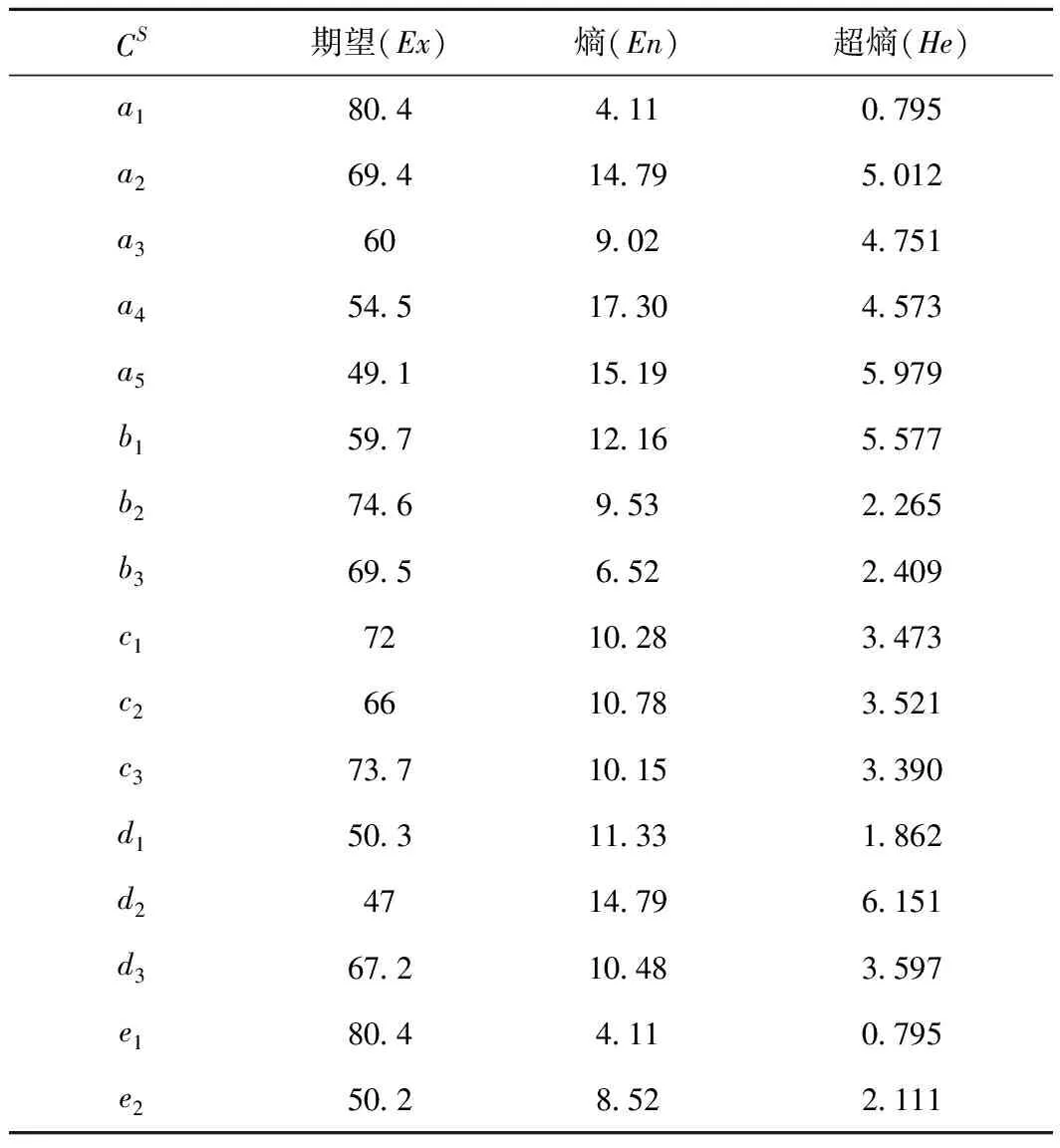
表3 底层指标严重度评估云数字特征

再根据式(11)、式(13)、式(15)计算出严重度综合评估云指标

CS(67.82，10.155，3.083)

同理可得可能性综合评估云指标

CP(47.667，9.0，2.589)

将综合评估云与评估标准云合并，如图5所示，其中红色的云表示相应的综合评估云模型。

图5 综合评估云

由图5可知，严重度综合评估云与评估标准云“特别严重的”最接近，即全电子化计算机联锁系统风险严重度等级为4级；可能性综合评估云与评估标准云“偶尔”最接近，即风险可能性等级为3级。根据表1，全电子化计算机联锁系统安全风险容忍等级为Ⅲ级，即不期望，与现场情况相符合，证明了本文所述评估方法的可行性及准确性。

4 结论

从系统安全风险评估的角度出发，引入最优组合赋权及云模型的理论，实现的功能及得出的结论如下。

(1)利用熵权法和层次分析法分别计算底层指标的客观权重和主观权重，又通过最优组合权重的方法将主、客观权重结合起来，得出底层指标的最合理权重。

(2)通过云发生器生成系统加权后的风险严重度评估云和风险可能性评估云，与标准云进行同图比较后得出严重度和可能性等级，实现了系统定性与定量评估的转化。

(3)通过实例分析，验证了所用最优组合赋权法下的云模型安全评估方法的可行性和准确性。

(4)文中的权重计算以及云生成器均使用Matlab软件编程实现，使得到的云模型以及评估结果更直观。

本文所提出的评估方法运用在全电子化计算机联锁系统的安全风险评估中，先采用分层分项计算权重，再将计算结果与云模型相结合绘制评估云，既保证了权重分配的合理性，又实现了系统的综合评估，为全电子联锁运营安全提供了一种可靠的分析方法，同时对铁路信号系统及其他领域的现场分析具有一定的利用价值。