相依性条件下滨海软土隧道盾构施工渗漏水风险评价
吴贤国,张文静,张立茂,姚春桥,曾铁梅
(1.华中科技大学土木工程与力学学院,武汉 430074;2.武汉地铁集团,武汉 430074)
滨海地区作为我国经济发展的引擎,基础设施建设不断完善,出现许多大型项目如地铁隧道等。但是滨海地区土质多为海相和湖相沉积的软土,施工难度大,易产生沉降、渗漏水等病害,故施工对专业技术要求更高,不确定性因素繁多。且现有关滨海软土盾构隧道渗漏水风险评价的研究多采用半理论与半经验方法,工程事故频繁发生。
现阶段已有许多关于盾构隧道渗漏水风险评价的研究。王岩,黄宏伟[1]通过建立影响地铁区间安全因素的层次结构模型,利用层次模糊综合评判法对地铁隧道安全体系进行评价。石建勋等[2]以杭徽高速公路隧道群渗漏水病害为例,应用改进的AHP对连拱隧道渗漏水体系进行了评价,并对其影响的大小进行排序。陈梦捷[3]等构建包含4个三级19个二级指标的地铁盾构法的施工阶段渗漏水评价体系,利用熵信息计算各指标的权重,建立基于模糊熵的盾构施工渗漏水风险评价模型。魏荣誉[4]采用有限元法对隧道施工、运营阶段的渗漏水病害相应机制进行仿真计算,并提出了渗漏水病害的处置技术措施。现有的评价方法定性成分较多,主观性较强,计算复杂,且均为考虑指标间的相依性关系。由于软土隧道盾构施工风险状态受到众多因素共同影响,同时各个因素之间也相互影响,已有的分析多从单一、独立、静态因素的角度对隧道施工结构风险状态进行分析,不够精确。
云模型对于定性概念和定量概念的处理具有强大优势,而Copula函数多用来捕捉风险因子间的相关关系。因此,提出在相依性条件下对隧道盾构施工风险结构进行风险感知,将相互影响的因素看作多维云,结合Copula相关理论,构建云-Copula模型,并进行综合隶属度计算,将其转化为该指标对各等级的精确信度,即D-S证据理论中的基本可信度分配,进行多证据条件下软土隧道盾构施工过程中渗漏水病害风险等级状态多源融合,识别评定渗漏水病害风险等级,为滨海软土隧道盾构施工过程中渗漏水风险评价提供了新的思路与方法。
1 相依性条件下施工风险评价步骤
相依性条件下滨海软土盾构隧道施工渗漏水风险评价的步骤如图1所示,主要包括:(1)云-Copula模型构建,并计算渗漏水病害对于各个风险等级的隶属度,将其转化为证据理论的BPA;(2)D-S证据融合,通过检验两两证据冲突与否,修正证据等将证据逐次两两融合,得到将不确定性降低后的证据融合结果,即渗漏水病害对于各个风险等级的隶属度;(3)风险感知,将步骤(2)中计算所得渗漏水病害的隶属度归一化,识别评定渗漏水病害风险等级,并根据评价结果给出相应的改进建议与措施。

图1 相依性条件风险感知流程
1.1 云-Copula模型构建
云模型是李德毅院士在传统概率统计和模糊集知识理论的前提下提出的定性定量不确定性转换模型[5]。设论域U={x1,x2,…,xm}是一个精确数值表示的定量论域,若定量值x∈U,C是U上的一个定性概念,且x是C的一次随机实现,x对C的确定度即隶属度μx∈[0,1]是有稳定倾向的随机数。
μ:U→[0,1] ∀x∈Ux→μ(x)
(1)
则x在U上的分布称为云(Cloud),每个x称为一个云滴。定性概念的整体定量特性可以用云的数字特征来反映,即用期望、熵和超熵3个数字特征即Ex、En、He来整体表征一个概念。
Copula函数的特点是可以用一维边缘分布将多维随机变量的联合分布连接起来,故也被称作相依函数、连接函数,来描述其对于多维变量的处理[6]。
则云-Copula模型构建过程如下。
Step 1:选取指标,划分等级状态
选取相互关联的指标,并依据工程的具体情况和相关要求,将各指标的安全状态等级划分为m个等级,并确定各个等级的区间,设指标X的第i等级的上下界限为(ximin,ximax)。
Step 2:选择Copula函数
因为不同变量之间的关联性存在不一致,故选取合适的Copula函数对研究各变量之间的相依性关系十分重要。本文选取最常用的Clayton Copula函数,其分布函数表达式[7]如式(2)所示,将指标实测值代入对应的Clayton函数中,进行相依性分析。
C(x,y;θ)=(x-θ+y-θ-1)-1/θ
(2)
Step3:计算Copula参数
Copula相关参数的选取是Copula函数运用中很重要的一步,本文采取Kendall秩相关系数法计算Copula相关参数,Kendall秩相关系数τ的计算可在Matlab中直接计算,二元变量和三元变量相关参数θ计算过程有所区别。
对于二元变量,Clayton Copula函数相关参数θ和Kendall相关系数τ之间具有如下关系
(3)
对于三元变量X,Y,Z,在利用Matlab计算出τXY,τYZ,τXZ后则需根据转换公式
(4)
进行转换之后得到相关系数θ。
Step 4:确定云-Copula模型区间
但由于Copula函数适用于描述单调变化变量,因此,根据云模型的具体特性,将指标X的第i等级(ximin,ximax)从Exi处分为两段,分别为(ximin,Exi)和(Exi,ximax);同理指标Y的第j等级(yjmin,yjmax)从Eyj处分为两段,分别为(yjmin,Eyj)和(Eyj,yjmax)。对三元变量X和Y,即可构建4个云-Copula模型,用等级区间表示即如式(5)所示
(ximin,Exi;yjmin,Eyj)
(ximin,Exi;Eyj,yjmax)
(Exi,ximax;yjmin,Eyj)
(Exi,ximax;Eyj,yjmax)
(5)
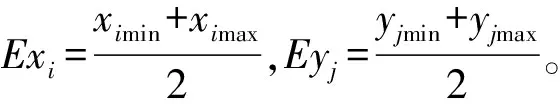
Step5:多维云模型特征值计算
针对n个指标的m个等级,分别构建云模型。以区间(ximin,Exi;yjmin,Eyj)对应的二维云模型为例,则该等级在x维和y维上特征值(Exxi,Enxi,Hexi)和(Exyj,Enyj,Heyj)按式(6)、式(7)计算,其中s为常量。
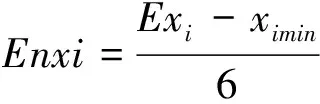
(6)
Hexi=s

(7)
Heyj=s
对二元变量X和Y,其一维云模型分别为(Exxi,Enxi,Hexi)与(Exyj,Enyj,Heyj),联合构建二维云模型(Exxi,Enxi,Hexi;Exyj,Enyj,Heyj);同理对三维变量X、Y和Z,其一维云模型分别为(Exxi,Enxi,Hexi)、(Exyj,Enyj,Heyj)和(Exzk,Enzk,Hezk),联合构建二维云模型(Exxi,Enxi,Hexi;Exyj,Enyj,Heyj;Exzk,Enzk,Hezk)。
Step6:云-Copula图绘制
对于二元变量和多元变量,从相依性角度分析变量的同时,考虑到变量的分布大多呈正态分布,因此将Copula函数与多维正态云隶属度计算函数结合起来,作为相依性条件下正态分布变量的隶属度计算。将正态云的隶属度计算值作为ClaytonCopula函数的自变量值,将ClaytonCopula函数的计算结果作为云-Copula模型的隶属度计算结果,利用Matlab软件即可绘制出二维云图。
μ(x1,x2,L,xn)=Cθ(F1(x),F2(x),L,Fn(x))
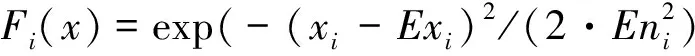
(8)

1.2 隶属度计算
Step 6:隶属度计算
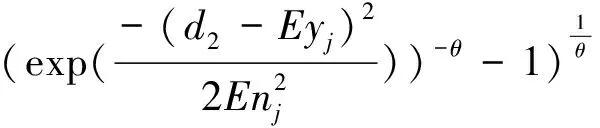
(9)
为确定实际施工中获得的一组具有相依性三维数据组实测数据(d1,d2,d3)对于第ij等级(ximin,ximax)、(yjmin,yjmax)的隶属度,综合式(2)与云模型正态隶属度公式,按照Copula函数和计算所得的相关参数,利用云-Copula模型隶属度计算公式,即可得该多维变量对该等级的隶属度。
1.3 D-S证据融合

(10)
则证据融合过程如下。
Step7:冲突检测
设mi,mj是两证据的基本可信度分配,对应焦元分别为X1,X2,…,Xn和Y1,Y2,…,Yn,按式(12)计算冲突系数k
A=X1∩X2
(11)
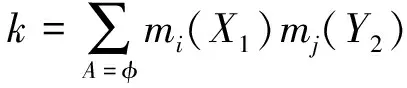
(12)
若冲突系数0≤k<1,表明证据不冲突(k值越大,证据冲突程度越大)可以使用式(11)的组合规则对两个证据进行融合操作。若k=1,则两个证据完全冲突,需进行修改证据源或者修改组合规则的方法进行修正,本文采取修改证据源的修正方法。
Step8:证据权重计算
根据欧式距离函数和已有的数据及性质,通过式(13)所示的公式来计算两证据体mi和mj间的距离。得到一个由两两证据距离排列的矩阵D,则mi和mj的相似测度Simij如式(14),证据体mi的支持度Sup(mi)为式(15),将所有Sup(mi)经过归一化处理后确定为证据mi的权重为式(16)。
(13)
Sim(mi,mj)=1-dij
(14)

(15)

(16)
Step9:证据替换
将式(16)得出的加权评价证据替换未产生冲突的证据,按式(17)、式(18)计算平均证据替换冲突证据。若不冲突按照(11)式融合;若冲突,按Step7~9步继续进行证据替换。
(17)

(18)
Step10:证据合成
按照两两证据合成,得到结果与下一个证据合成的原则依次合成,直到所有的证据体都合成完毕。合成得到的最终状态的不确定性大小用m衡量,计算如式(19)。称m为不确定性系数,合成得到的最终状态的不确定性越小,则计算出的m值越小,则结果的可信度越高。
(19)
2 实证分析
2.1 工程概况与特点
(1)工程概况
宁波市轨道交通1号线一期工程从西部市区的高桥镇开始到终点站东外环路站,客观上存在较大的地质、环境和施工风险:①地质条件差,沿线范围内车站基坑底与隧道洞身主要位于25~40m厚的海相淤泥质软土和粉质黏土、淤泥质粉质黏土地层,且局部区段为填河区,存在厚填土层与下卧淤泥层,容易产生不均匀沉降、震陷和局部粉细砂液化问题;②穿越城市主干道;③穿越或邻近重要建(构)筑物;④地下管线与防空洞密集;⑤多次穿越河流。
(2)渗漏水病害风险评价指标体系
通过工程实践和文献查阅,将从水文地质条件、防水密封材料、止水条、管片拼装、注浆质量、衬砌混凝土自防水等六个方面来分析软土盾构隧道施工过程中的渗漏水病害的影响因素和风险等级[9-10],具体指标选取见图2。通过对图2的分析可知,设每个二级指标Di(i=1,2,…,6)下的三级指标有Ni个,则分别有N1=N5=3,N2=N3=N4=N6=2。
2.2 云-Copula模型构建
对于N=2的指标D2、D3、D4、D6将进行云-Copula二维云图绘制及建模进行风险评价过程,由于难以在普通三维空间对多维云进行表示,对于N=3的指标D1、D5,仅进行云-Copula风险评价,步骤如下。
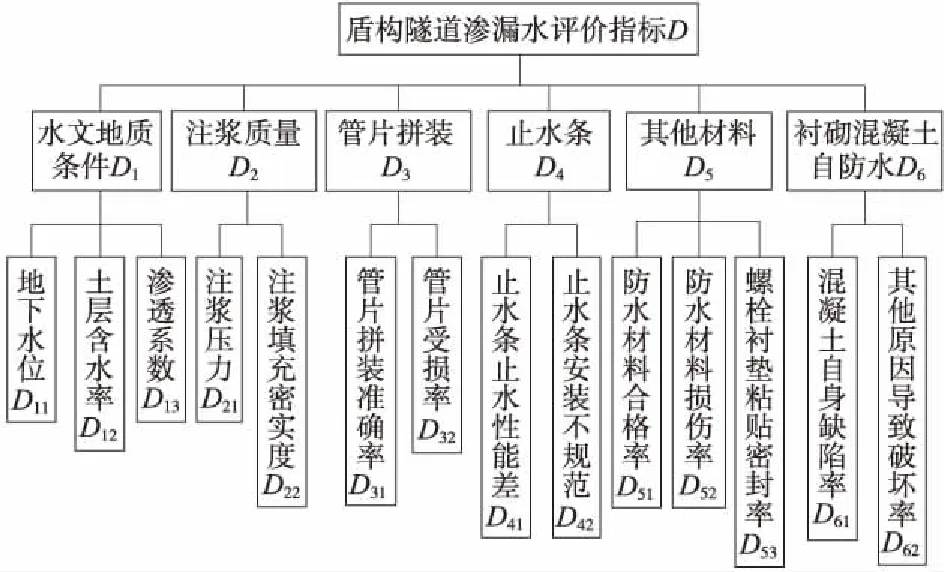
图2 盾构隧道渗漏水评价指标
(1)划分指标等级状态
基于文献[11],根据衬砌渗漏水量的大小及渗漏状态分为:渗润、滴水、流水、喷水、淋瀑5种,结合文献[12],将5种状态分别对应于5个状态区间,分为Ⅰ级(安全)、Ⅱ级(较安全)、Ⅲ级(基本安全)、Ⅳ级(较危险)、Ⅴ级(危险),以水文地质条件D1、注浆质量D2为例列出等级状态划分,见表1。
(2)监测数据获取及Coupla参数计算
根据监测要求和监测方法,跟踪获取宁波地铁1号线一期工程的14个风险因子监测数据,共100组,选用Matlab内置程序输入历史监测数据计算相关系数τ。对于水文地质条件D1,根据地下水位D11、土层含水率D12、渗透系数D13的实测数据,得到Kendall秩相关系数τ12=0.256 4,τ13=0.179 5,τ23=0.564 1。再分别按照式(3)计算Clayton函数的相关参数为θ=1.679 2。同理对于注浆质量D2,计算注浆压力D21和注浆填充密实度D22的Kendall秩相关系数τ=0.134 8,按照式(2)计算Clayton函数的相关参数为θ=0.311 6。
(3)二维云-Coupla模型特征值计算
此步骤仅针对于N=2的指标计算其云-Coupla模型特征值,表2为注浆压力和注浆填充密实度指标的一维云模型组合构建的二维云,其中两行特征值中第一行为注浆填充密实度云模型的特征值,第二行为注浆压力云模型的特征值。

表1 指标等级划分结果

表2 二维云模型
(4)云-Coupla模型图绘制
对注浆质量D2按照表2中所列的25个二维云模型分别构建云-Copula模型,以注浆压力和注浆填充密实度指标的等级Ⅰ为例构建4个云-Copula模型,用等级区间表示分别为(0,0.325;0.98,0.99)、(0,0.25;0.99,1.0)、(0.25,0.5;0.98,0.99)、(0.325,0.35;0.99,1.0)。在Matlab中绘制该单个云-Copula模型,以ClaytonCopula函数为例,其二维平面如图3所示,三维立面如图4所示,将4个云图拼在一起,可得到注浆压力和注浆填充密实度指标的关于等级Ⅰ的云-Copula模型的平面和立面,如图5所示,同理,可构建这两个指标关于其他等级的共24个云-Copula模型。
2.3 软土隧道盾构施工风险评价
(1)隶属度计算与风险分析
①东-江区间1号段实测数据

图3 云-Copula区间平面
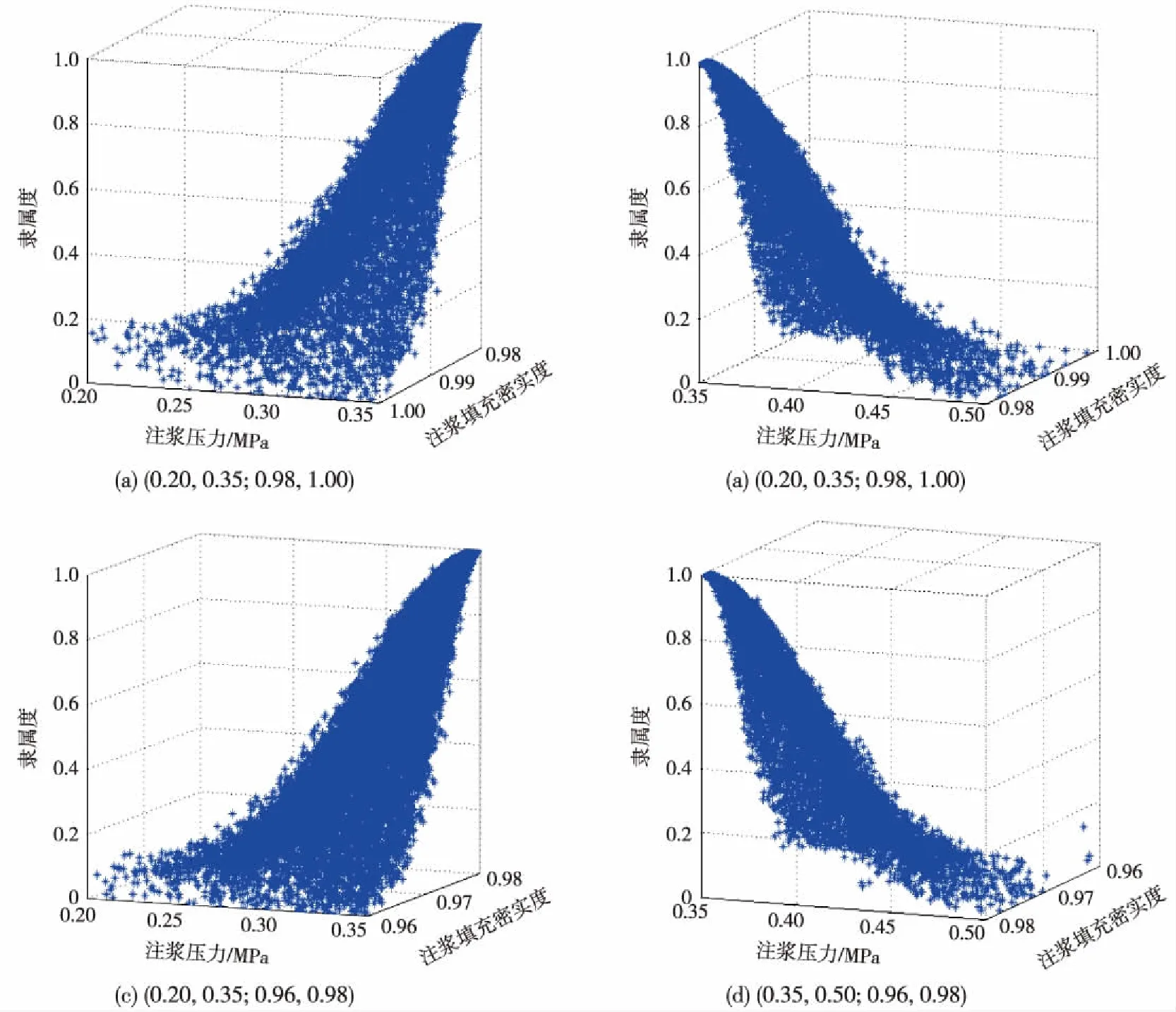
图4 云-Copula区间立面

图5 云-Copula模型
在对于宁波市轨道交通1号线一期工程按上节所述步骤构建云-Copula函数后,针对于东门口(天一广场站)—江厦桥东站施工过程中的1号检测区段的实际检测数据,进行如下计算。
②隶属度计算
a.N=2指标隶属度计算
对于N=2的二级指标,同样以注浆压力D21和注浆填充密度D22为例进行计算隶属度,其结果表示注浆压力和注浆填充密度在相互作用下其上级指标注浆质量D2对各个等级的隶属程度,ClaytonCopula函数的计算结果如表3所示。
b.N=3指标隶属度计算
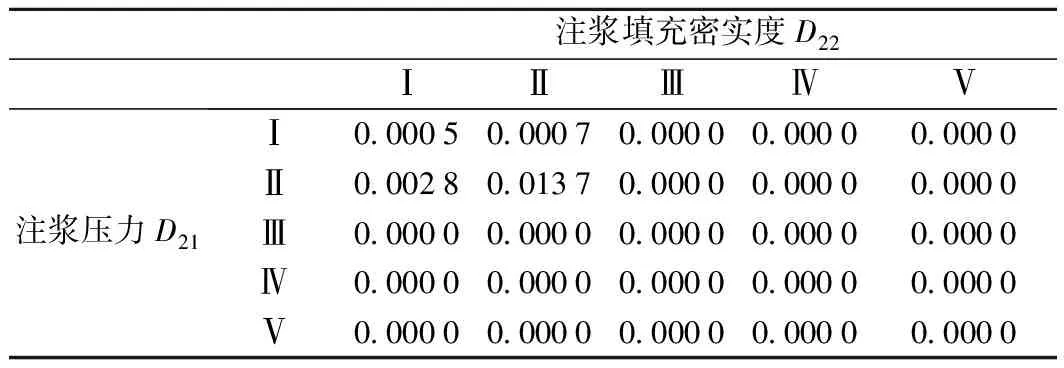
表3 注浆填充密实度和注浆压力对各等级隶属度
对于N=3的二级指标,ClaytonCopula函数的计算结果如表4所示。以水文地质条件D1为例,其结果表示地下水位和土层含水率及渗透系数在相互作用的相依性条件下,上级指标水文地质条件对各个等级的隶属程度。

表4 相依性条件下N=3二级指标对各等级的隶属度
③隶属度汇总
a.等级划分原则
对于N=2的指标,按照如图6所示的区间等级划分示意图的原则进行累加,图中列出5×5顺序排列矩阵中所有标注Ⅰ矩形计算出的隶属度值叠加和表示融合后因子对于等级Ⅰ的隶属度,其他等级以此类推。而对于N=3的指标,依照N=2的指标的累加原则并以此类推至三维空间的累加,此处便不作绘图显示。

Ⅰ级Ⅱ级Ⅲ级Ⅳ级Ⅴ级Ⅰ级Ⅱ级Ⅲ级Ⅳ级Ⅴ级ⅠⅠⅡⅢⅣⅠⅡⅡⅢⅣⅡⅡⅢⅢⅣⅢⅢⅢⅣⅤⅣⅣⅣⅤⅤ
图6 区间等级划分示意
b.隶属度汇总结果
分别对于N=2及N=3的二级指标对同一等级的隶属度进行累加,在云-Copula模型的运算下,汇总后的各上级指标对各等级的隶属度如表5所示,m(Θ)为不确定性系数。表中加粗数字为五个等级对应数字中最大的数字,表示目前该指标隶属于该等级的程度最高,亦表示该指标隶属于该等级的精确信度越大。
(2)基于D-S证据理论的融合评价
把水文地质条件D1、注浆质量D2、管片拼装D3、止水条D4、其他材料D5、衬砌混凝土自防水D6这六个指标分别作为证据体,则环境Θ={D1,D2,D3,D4,D5,D6}。按式(10)计算冲突系数,得到两两证据体之间的冲突系数均在0~1,故证据之间不冲突。分别将水文地质条件和注浆质量作为证据体融合、融合结果与管片拼装融合、该结果与止水条融合、该结果与其他材料融合,最后结果再与衬砌混凝土自防水进行融合,可得到1号段隧道该套监测值下渗漏水病害的风险状态,具体结果如表6所示。其中数据组编号①代表融合之后的各指标Di与环境Θ的隶属度分配情况,数据组②代表各指标对于等级Ⅰ~Ⅴ的隶属度经过归一化处理后的结果。

表5 各指标与环境隶属度分配

表6 1号段隧道渗漏水风险状态决策融合结果
从表6的数据组编号①可以发现,相对于表6中的对于环境Θ的隶属度分配m(Θ)也称不确定性系数是不断在降低的。说明在融合的过程中,各指标对于各风险等级解释程度越来越大,相应的不确定性越来越小,概率的分配越来越科学,利用率越来越高。从数据组编号②可以发现,1号段隧道目前处于等级Ⅰ(安全),但是对于安全等级Ⅱ(较安全)的隶属度也很大,即有向安全等级Ⅱ发展的趋势,但状态仍然是安全的。这与实际检测的结果(图7)相同,即衬砌渗漏水量状态为渗润伴随轻微滴水。故对危险性较大的二级指标即注浆质量D2、止水条D4、衬砌混凝土自防水D6加强监测与控制,从原材料、施工过程及养护等角度制定控制建议与意见并实施,一段时间以后,渗漏水得到了有效的控制,隧道仅有轻微渗润,如图8所示,即1号段隧道的渗漏水病害得到有效控制。

图7 1号段隧道原状态

图8 1号段隧道调整后状态
3 结论
本文对宁波市轨道交通1号线一期工程某检测区段盾构施工过程中的渗漏水风险构建指标体系,基于云-Copula模型在考虑各个风险因子的相依性下对该指标体系的二级指标进行风险衡量,再利用D-S证据理论进行证据融合,从而得出该检测区间渗漏水病害风险状态,为滨海软土盾构隧道施工过程中的风险评价与管理提供了一种新的思路与方法,结论如下。
(1)借助云模型的定量定性转换优势及Copula函数的相依性处理,提出一种云-Copula模型的相依性条件下风险感知及评估方法,为含有相关风险因子的风险指标分析提供了一种新的建模分析方法。将云-Copula模型转化为D-S证据理论中基本可信度分配进行证据融合,提出实现有效的多源异构融合的方法和具体步骤。
(2)将基于云-Copula模型和D-S证据理论的多源异构融合评价方法,运用于宁波轨道交通1号线一期工程东—大区间的1号检测区间的渗漏水病害的风险评价,得出该监测区段水文地质条件、管片拼装和其他材料三类指标目前均处于等级Ⅰ安全等级,注浆质量和衬砌混凝土自防水指标处于等级Ⅱ较安全等级,而止水条止水性能指标当前处于等级Ⅲ,处于基本安全的状态。
(3)将利用云-Copula模型计算出的各个二级指标对各个等级的隶属度作为D-S证据融合的基本可信度分配,并进行决策融合。融合结果分析发现,经过融合这个过程,降低了整体风险评价的不确定性,得出该段检测区段隧道处于Ⅰ安全等级,但有即将发展为Ⅱ安全等级,可以尽量采取措施来控制的结论。

