以气象参数预测的输电线最大载流量概率模型

张 斌, 金 涛, 江岳文, 叶 荣, 温步瀛

(1. 福州大学电气工程与自动化学院， 福建 福州 350116；2. 国网福建省电力有限公司经济技术研究院， 福建 福州 350003)

0 引言

当电力工业蓬勃发展时， 人们对电力需求的增长速度远高于输电基础设施发展的速度， 当前的许多输电线路已经从稳定限制转变为热限制. 传统上， 输电线路的传输容量定义是根据设计要求， 即在严酷环境条件下计算出来的最大恒定电流， 以满足电网的安全可靠运行， 但未能充分挖掘输电线路的输电潜力. 20世纪70年代， Davis[2-3]针对输电线路提出动态热定值这一概念. 动态热定值(DTLR)方法意味着输电线路的容量根据实时天气条件动态地变化， 因此气象条件对线路的输送容量具有很大的影响.

随着近几十年的不断发展， 动态热定值技术越来越成熟. 文在传统法基础上对载流量算法进行加权求和改进， 只能在一段时间的某些时刻能减小载流量的波动； 文提出动态增容系统的总体构架及软硬件设计等， 计算出输电断面动态限值和增容过程中安全的评估； 文通过对历史气象数据的分析， 实现不同时间尺度下的计算输电线路的动态热定值， 并将此定值结果用于配电网可靠性分析.

由于大数据分析技术在电力系统中得到广泛的应用， 越来越多的研究者从概率统计角度出发研究动态热定值. 文提出一种基于分位数回归分析理论的新的概率预测方法， 以实现架空输电线路载流量的概率预测， 该方法将实时载流量和显著影响的天气参数嵌入分位数回归预测模型中， 然后获得载流量的点预测和区间预测结果； 文在考虑天气变量不确定性的情况下， 采用概率和模糊估计的方法对线路的动态热定值进行了比较， 在不同的跨距下计算截面载流量， 然后将计算出来的截面最小载流量值定义为线路的热定值； 文基于Bayes时间序列统计方法， 根据实时运行状态的数据进行输电容量的概率故障预测和风险评估， 但该方法是在低质量数据上进行粗略的检验， 精度不足.

本方法的创新点在于： 在不增加输电线路实时监测装置的数量， 基于优化组合核极限学习机对历史气象数据进行统计并预测， 将预测结果用于热平衡方程， 同时， 采用基于概率密度函数的方法对输电线路载流量以四季的时间序列进行概率分析. 将某地区实际数据与该模型计算出来的值相比较， 验证了所提出的建模方法的合理性.

1 载流量与气象参数的关系

计算最大载流量的公式有很多， 目前常用的有IEEE 2006-738标准[10]、 《110 kV～750 kV架空输电线路设计规范》[11]、 摩尔根公式12. 其基本原理都来自热平衡方程， 即当导线处于热平衡状态时， 其吸热功率与放热功率相等， 则有：

I2R(TC)+WS=WR+WF

(1)

其中：WS为日照吸热功率；WR为辐射散热功率；WF为对流散热功率；TC为导线温度；R(TC)为温度TC时导线交流电阻；I为导线载流量.

1) 辐射散热公式WR为：

(2)

其中：D为导线直径；ε为导线辐射散热系数， 取值区间为[0.9, 0.95]；θa、θp分别为导线环境温度和最大允许温度.

2) 对流散热功率WF为：

(3)

其中：vw为风速；ρ为空气密度；μ为空气动态粘度；kf为空气热传导率；ka为风向因子; 参数ρ、μ、kf和ka的具体表达式见文[13]

3) 日照吸热功率WS为:

WS=αJD

(4)

其中：α为导线表面吸热系数， 光亮新线取0.35～0.46， 旧线或涂黑色防腐剂线取0.9～0.95；J为日光对导线的日照强度.

4) 交流电阻值为：

(5)

其中：R(Thigh)是温度为Thigh时的导线交流电阻；R(Tlow)是温度为Tlow时的导线交流电阻. 由经验值可得， 当选取Thigh为75 ℃，Tlow为25 ℃温度下导线的电阻值与实际的电阻值之间的误差是可以忽略的.

2 气象参数的EMD-PSO-KELM预测模型

文中的环境温度和风速的历史数据来源于福建省气象局， 日照强度的历史数据来源于中国气象局气象信息中心资料服务室， 收集时间自2010年1月1日到2016年12月31日. 由于篇幅有限， 仅以环境温度预测为例， 温度信号波形如图1所示.

2.1 温度信号的经验模态分解

经验模态分解(empirical mode decomposition， EMD)是一种自适应信号分解的方法， 将原始信号按时间序列分解出的若干个固有模态函数(intrinsic mode function， IMF)和一个余项， 这些IMF彼此之间影响较少且具有不同的尺度[14-15].

温度信号的经验模态分解过程如下： 首先找出原始数据序列x(t)中的极大值和极小值； 然后利用三次样条函数插值分别连接原始信号的所有极大值点和极小值点， 形成上包络线和下包络线， 然后计算上下包络线的均值m1(t)； 最后计算原始数据序列x(t)与包络线均值m1(t)之差， 若还存在负的局部极大值和正的局部极小值， 说明这还不是一个本征模函数， 需要继续进行“筛选”， 直至两者之差为常数. 原始信号序列x(t)可表示为IMF与余项之和， 即

(6)

对原始环境温度数据序列进行EMD分解， 依次分解出不同的IMF分量， 环境温度数据被分解成5个波动较小的分量和1个剩余分量. 分解结果如图2所示.

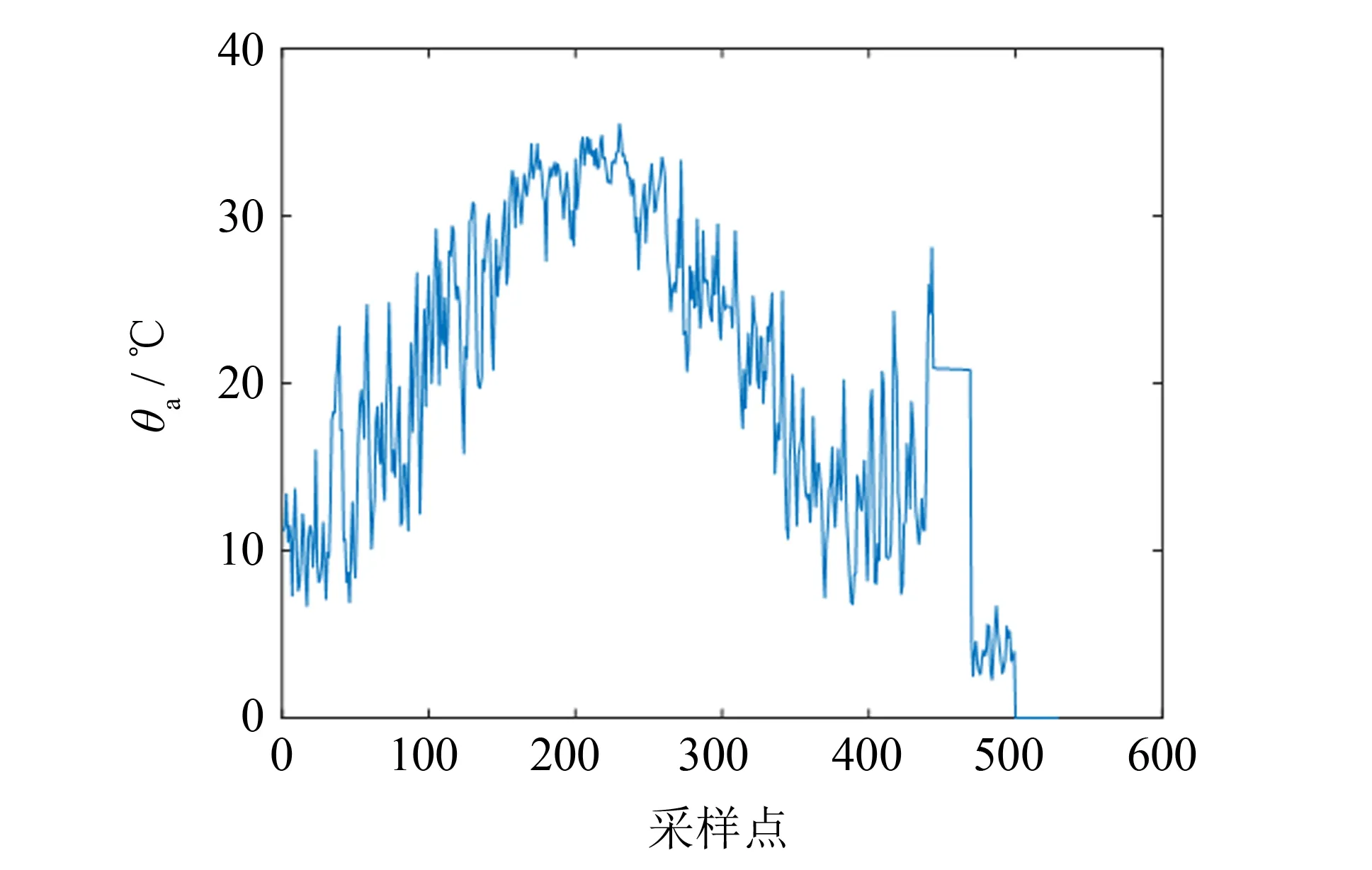
图1 环境温度信号波形Fig.1 Ambient temperature signal waveform

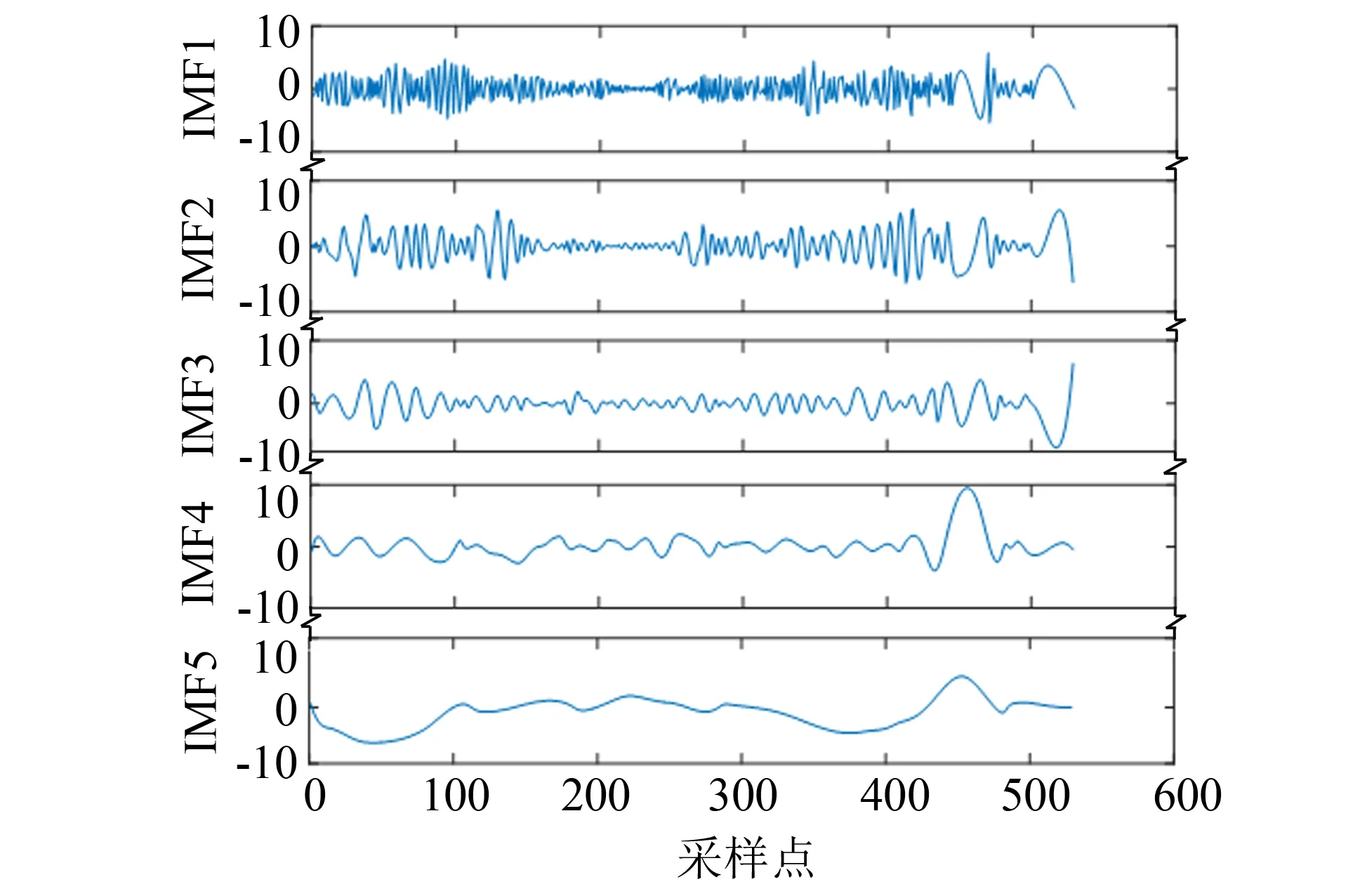
图2 温度信号EMD分解结果Fig.2 Temperature signal EMD decomposition result

2.2 温度信号的EMD-PSO-KELM预测分析

为进一步增强极限学习机的稳定性和泛化性能， 黄教授通过对比支持向量机(SVM)的原理， 把核函数引入到极限学习机中， 提出了KELM的算法[16]. 粒子群优化(particle swarm optimization, PSO)算法是一种群体智能的优化算法， 该算法最早由Kennedy和Eberhart[17]在1995年提出的， 该算法源自对鸟类捕食问题的研究. 基于EMD-PSO-KELM算法[18]的温度预测步骤如下：

步骤1 温度原始数据经过EMD分解成5个IMF分量；

步骤2 用KELM分别对各个分量进行预测；

步骤3 采用PSO优化KELM中两个参数， 即惩罚因子和核参数， 把这两个参数作为粒子群的输入， 以KELM输出的预测均方根误差最小作为粒子群的适应度来进行交叉验证获得最佳的惩罚因子和核参数；

步骤4 通过各个分量的预测结果重构出温度的预测结果， 并输出最优参数和最优模型.

将286组温度数据分成训练样本和测试样本， 将199 组数据作为训练数据， 后面87 组作为测试数据， 用于验证预测结果的好坏. 设定PSO 算法的最大迭代次数为30， 种群大小为20. 其中IMF分量单独预测结果如图3所示， 由于篇幅限制， 只给出IMF2和IMF4的PSO-KELM预测结果. EMD-PSO-KELM温度预测结果如图4所示.

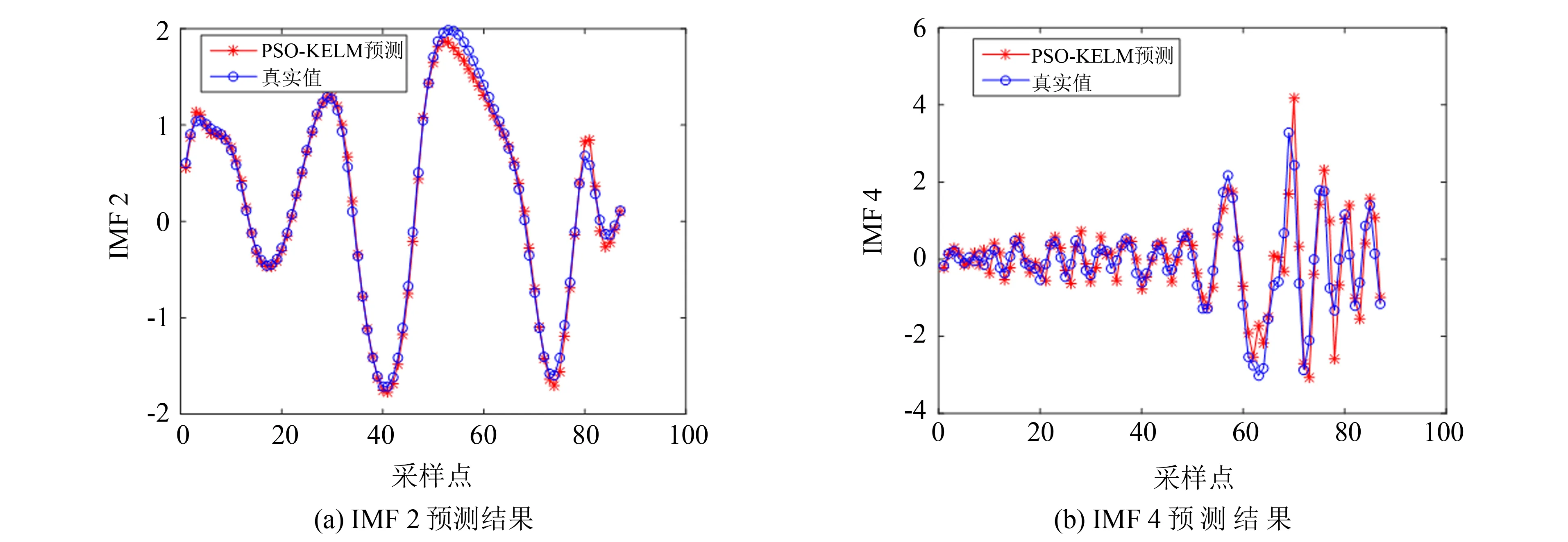
图3 IMF2和IMF4预测结果Fig.3 IMF2 and IMF4 prediction results

EMD-PSO-KELM温度预测的相对误差如图5所示. 由图5可以看出， 温度预测的相对误差约为-0.10～0.15， 在可接受误差范围之内. 由图3和图4可以看出， EMD综合预测结果要比单个IMF预测精度高， 是一种有效的温度预测方法.

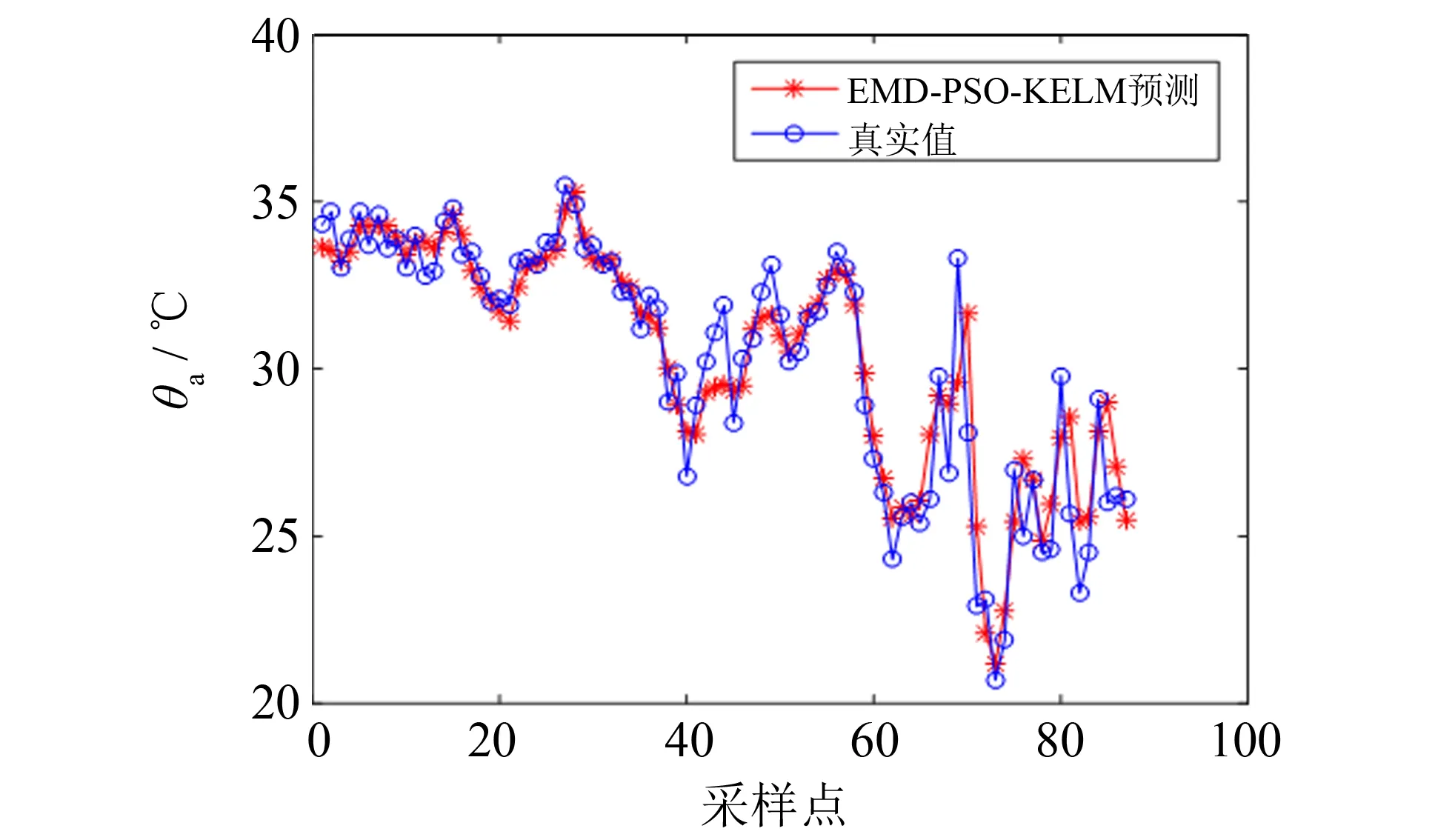
图4 EMD-PSO-KELM温度预测结果Fig.4 EMD-PSO-KELM temperature prediction results

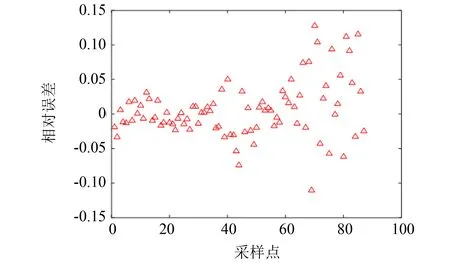
图5 EMD-PSO-KELM温度预测相对误差图Fig.5 EMD-PSO-KELM temperature prediction relative error map

为对比EMD-PSO-KELM算法的优越性， 将EMD-PSO-KELM 算法、 EMD- KELM算法、 PSO-KELM算法和普通BP算法四者的温度预测结果进行对比. EMD- KELM算法、 PSO-KELM 算法和普通BP算法温度预测结果如图 6所示. 其相对误差、 均方根误差(MSE)和相关系数(R2)对比结果如表1所示.

由图6和表1可以看出， EMD-KELM算法对于温度数据的预测效果好于PSO-KELM和普通BP算法， 同时， 本算法EMD-PSO-KELM相对误差和MSE明显小于其它三种算法， 温度预测数据

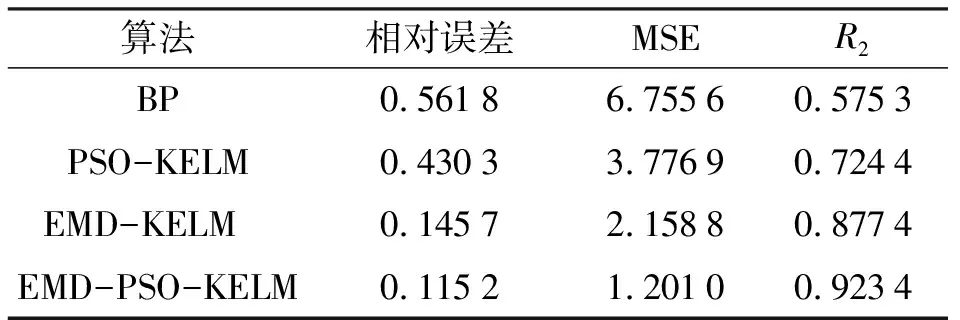
表1 四种算法温度预测的结果对比

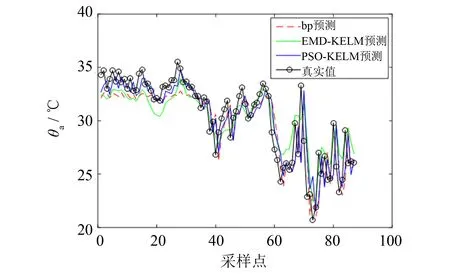
图6 其他3种算法温度预测结果对比Fig.6 Comparison of temperature prediction results of the other 3 algorithms

与原始数据的相关系数为0.923 4， 明显高于其它算法， 说明本算法EMD-PSO-KELM对于温度数据的预测效果最好. 风速和日照强度的预测结果同温度预测效果类似.

3 输电线路载流量的概率模型计算与分析

在气象要素中， 温度和日照强度遵从正态分布[19]， 其正态分布密度函数如式(7)～(8)所示； 风速服从威布尔分布[20]， 其威布尔密度函数如式(9)所示. 由2.2节EMD-PSO-KELM预测的数据样本， 拟合可得参数μ=28.152 6，σ=11.262 3，γ=683.324 6，δ=67.768 3，a=5.985 6,b=12.458 7.

(7)

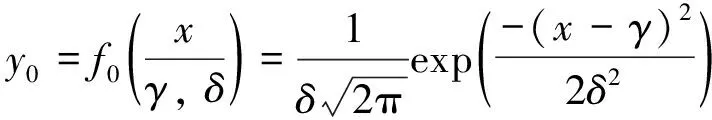
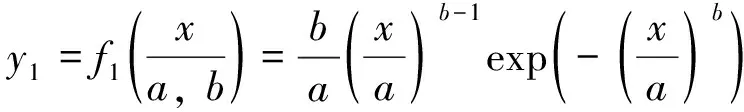
由2.2节EMD-PSO-KELM气象预测模型预测出来的环境温度、 风速和日照强度气象数据， 并结合热平衡方程即公式(1)， 可画出环境温度、 风速和日照强度与载流量之间的关系， 如图7～9所示. 由图7可以看出， 线路周围的风速增加， 使导线散热加快， 从而提高线路载流能力. 从图8和图9可得， 环境温度升高和日照强度的增大会使线路载流能力下降， 与此同时用户用电需求量更大， 所以在用电高峰期需要采取相应的增容措施.

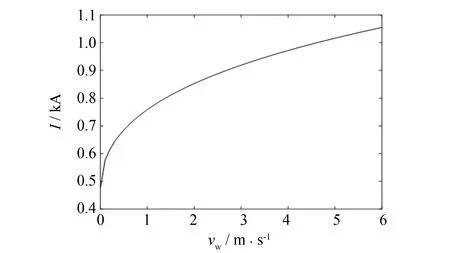
图7 风速-载流量关系图Fig.7 Wind speed-carrying capacity diagram

图8 环境温度-实时载流量关系图Fig.8 Ambient temperature-current carrying capacity diagram

以LGJ400/25导线为例， 根据式(1)， 已知环境温度、 日照强度和风速分布函数条件下， 可以建立基于概率密度函数的载流量概率模型， 以春夏秋冬四季为时间序列， 画出载流量全天24 h的概率密度分布， 如图10所示. 结合图10可得载流量的均值、 标准差和95%置信区间， 如表2所示.

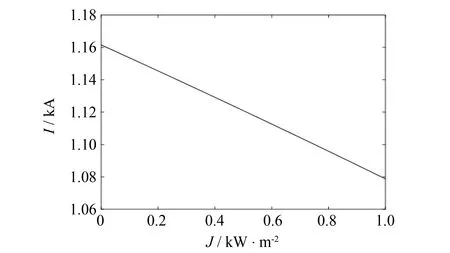
图9 日照强度-载流量关系图Fig.9 Sunshine intensity-carrying capacity diagram

图10 载流量概率密度函数Fig.10 Load capacity probability density function

从表2可得， 四季载流量均值按从小到大排序为： 夏、 春、 秋、 冬. 夏季环境温度高， 日照强度大且风速低， 故载流量小； 冬天环境温度低， 日照强度小和风速高， 故载流量大， 这符合实际情况. 四季载流量的标准差数值不大， 说明了载流量分散程度一般.

表2 描述性统计

注： 表2中置信区间为95%

4 算例电网的最大载流量动态分析

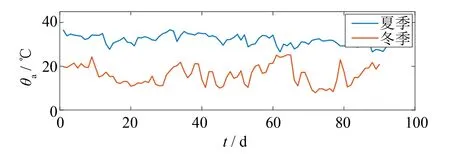
图11 环境温度曲线Fig.11 Ambient temperature curve

将上述气象预测方法和概率模型应用于该地区的110 kV输电线路的动态增容分析中. 计算中， 根据气候监测中心的实时微气象条件， 导线最大允许温度设为70 ℃， 计算线路的每天最大允许载流量， 所得结果与线路实际载流量进行比较. 2013年夏季和冬季期间， 采用该模型对该地区某风电场的输电容量进行分析， 且对环境温度、 风速和日照强度、 实际运行载流和安全载流限额进行统计与计算， 结果如图11～图15所示.

图12 风速曲线图Fig.12 Wind speed curve

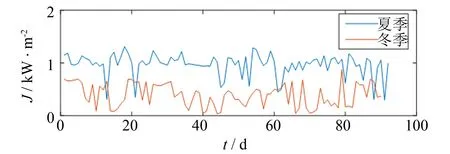
图13 日照强度曲线Fig.13 Sunshine intensity curve

图14 夏季动态增容情况曲线Fig.14 Summer dynamic capacity curve

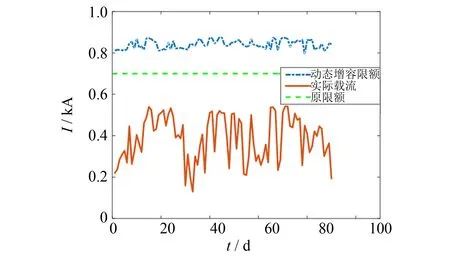
图15 冬季动态增容情况曲线Fig.15 Winter dynamic capacity curve

图11～图13为某地区夏季和冬季各三个月的环境温度、 风速和日照强度变化曲线图. 图14～图15中， 在夏季和冬季的时间段里， 根据SCADA系统采集的电流数据， 夏季中， 在7月15日9:00时， 出现导线最大的实际载流值， 为501.6 A； 冬季中， 在12月15日10:00时， 其最大实际载流量值为569.1 A. 动态增容的载流量安全限额比原限额700.0 A有所提高， 夏季和冬季中， 达到最低计算值分别为737.5和792.8 A， 相比与原限额增加了37.5和92.8 A， 约提高了5.4%和13.3%. 由表2可知， 该模型在95%置信度水平下， 夏季和冬季的载流量区间为[718．759 4，727．941 0]和[860．870 3，872．232 . 当图10中的载流量概率密度函数处于峰值时， 夏季和冬季的载流量分别为724.0和866.0 A， 即其值出现的频率是最高的. 所以在夏季空调等制冷用电设备增多和冬季暖气设备开启， 用电需求量大幅度增加， 输电线路的输送容量可适当提高限额， 夏季可提高到724.0 A， 冬季可提高到866.0 A， 以满足用电高峰期用电量的需求.

5 结语

为提高输电线路的输电能力， 且在不增加线路实时监测装置的数量情况下， 以四季为时间序列对某地区的历史气象数据进行统计， 构建出基于EMD-PSO-KELM的气象预测模型， 通过理论分析和建立载流量概率模型可得出如下结论.

1) 提出的EMD-PSO-KELM算法预测精度明显优于其它算法模型， 且对环境温度、 日照强度和风速拟合效果较好. 所以用该模型对该地区的环境温度、 日照强度和风速进行一段时间的预测， 然后将预测出来数据样本作为概率模型的源数据.

2) 实际输电线路中输送的载流是在保守环境下获得的， 故输电线路中还存在很大的输电潜力， 通过建立载流量概率密度函数的概率模型分析可得， 在确保输电线路安全可靠运行情况下， 夏季和冬季输送容量可分别适当提高， 即输送限额可大于原限额， 这样不仅可以缓解用电高峰期电力紧张的矛盾， 而且会给电网带来一定的经济效益.