模糊控制的光伏发电MPPT系统设计
章达宾, 朱其祥, 张家齐
(福建船政交通职业学院安全技术与环境工程系, 福建 福州 350007)
0 引言
最大功率点跟踪技术(maximum power point tracking, MPPT)是光伏电池的研究热点之一. 目前MPPT技术主要包括查表法、 扰动观察法、 电导增量法、 人工神经网络算法[1]、 模糊逻辑控制法等. 其中, 查表法由于没有真正实现在线实时跟踪与控制, 误差相对较大. 扰动观察法控制目标较盲目, 光伏电池的工作点总是在最大功率点附近不断变化, 导致一定功率损失, 影响并网电流质量, 甚至出现方向判断错误的情况. 电导增量法控制精度较高, 响应速度较快, 输出电压能够较平稳跟踪变化, 而且稳态的振荡比扰动观测法小, 避免扰动观察法等方法的盲目调节. 人工神经网络算法虽然能够处理非线性系统对象, 但过多地依赖于样本数量和精度, 对于不同的光伏电池系统需要进行各自针对性的训练, 因此实现起来较为困难, 存在局限性. 模糊逻辑控制法控制精度较高, 对被控对象的数学模型准确性要求较低, 适合难以建立准确数学模型以及受外界条件影响的控制系统[4-5]. 目前主要模糊控制是将功率对电压或者电流的变化率当作模糊输入变量, 依据专家经验作出模糊判别, 给出调节输出的隶属度, 由隶属度值完成反模糊化处理, 从而改变控制调节量, 获得控制最大的功率输出[6-8]. 与目前其他采用电导增量法和模糊控制法不同的是, 本方案最后还利用修正因子C对控制输出进行进一步修正. 修正后的控制输出量结合了电导增量法和模糊控制法的切换点参数以及误差变化量, 并随着与最大功率点的距离而改变大小, 控制效果更强, 更精细.
1 电导增量法及改进
1.1 光伏电池输出功率数学模型
一般光伏电池5个重要参数分别为: 开路电压Uoc, 短路电流Isc, 最大功率点输出功率Pmax, 最大功
率点处的电压Um, 最大功率点处的电流Im. 这5个参数可以通过测试得到. 图1为光伏电池的I-U和P-U特性曲线[10]. 曲线上各参数的计算如下:
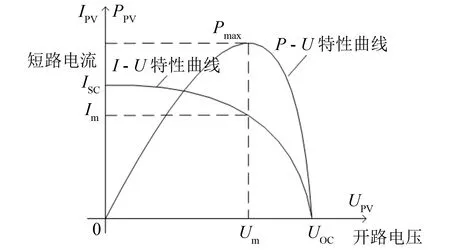
图1 光伏电池的I-U和P-U特性曲线Fig.1 I-U characteristic curve of photovoltaic cell
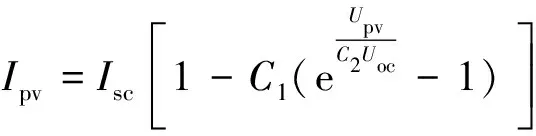
其中, 在光伏电池最大功率时:
如果是光伏阵列:
(2)
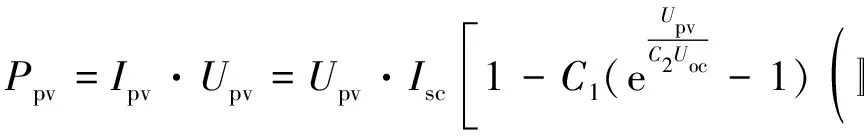
光照强度和光伏电池结温是影响输出功率的最重要参数, 且光照强度又影响结温的变化. 光照强度的上升将增大输出短路电流Isc和最大功率点电流Im, 但对输出开路电压Uoc和最大功率点电压Um影响不大. 结温上升将使开路电压Uoc和最大功率点电压Um线性降低, 对短路电流Isc和最大功率点电流Im影响较小, 只是略为增加.
1.2 电导增量算法及改进
依文[11], 光伏电池P-U特性曲线最大功率点处满足下式:
(4)
其中:G为瞬间电导值, ΔG为电导增量.
因此, 控制最大功率点的算法如下: 当G+ΔG>0, 即dPPVdUPV>0时, 需要增大参考电压, 或者通过调整负载等效阻抗来增加功率输出; 当G+ΔG<0, 即dPPVdUPV<0时, 按照相反方向调节[11-12]. 电导增量法主要是通过对光伏电池电导增量以及瞬间电导值的正负极性的比较来决定系统的控制信号.
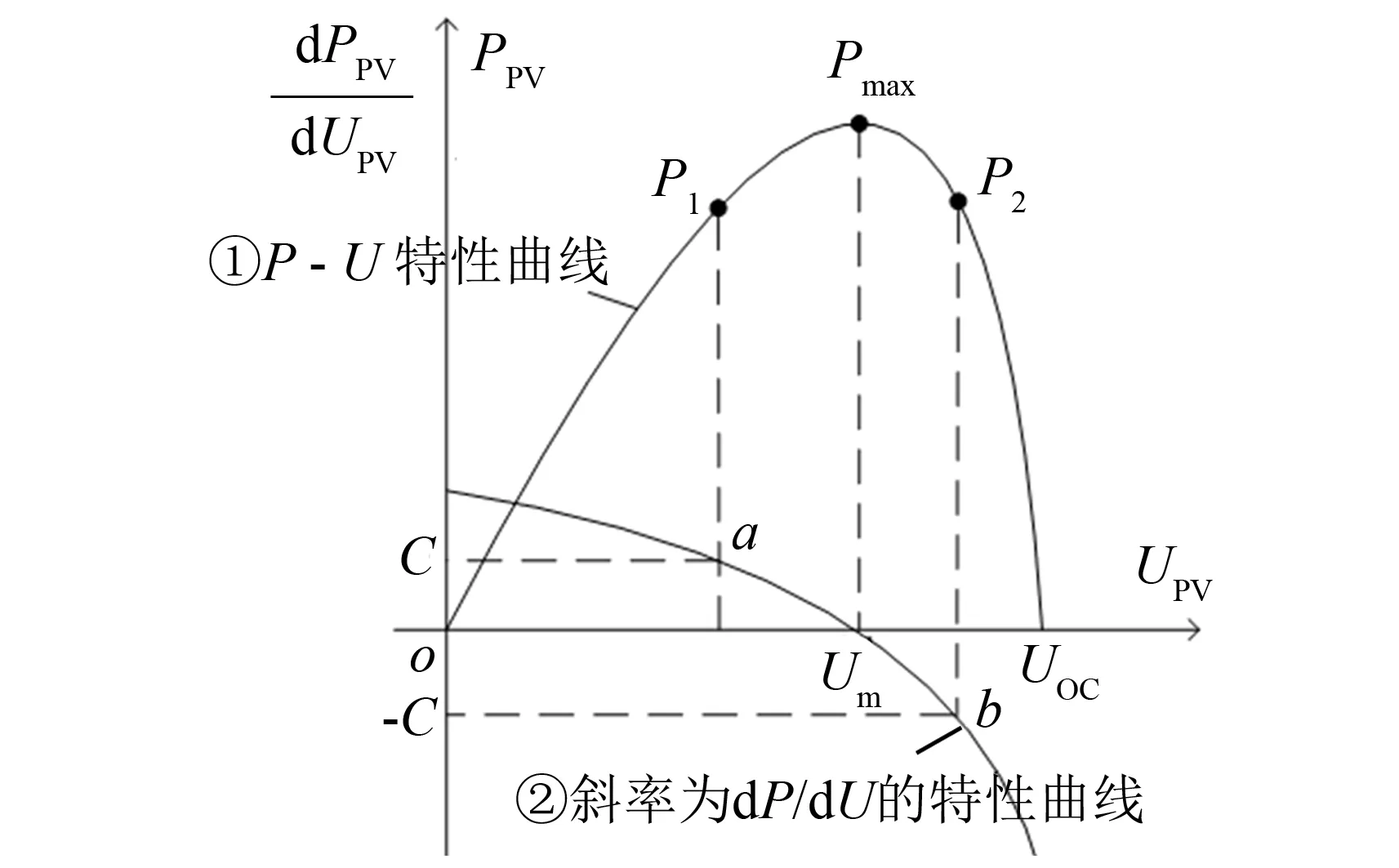
图2 电导增量法MPPT示意图Fig.2 Schematic diagram of conductance increment method MPPT
在光伏发电的MPPT控制上, 可以分两步进行. 在系统启动时或者运行期间受外部光照和温度变化造成输出功率偏离最大功率点较远时, 采取动态响应快的电导增量法来控制, 以便输出功率尽快接近最大功率点; 之后采用引用修正因子的改进模糊控制策略对系统进行控制, 以保证MPPT的稳定的稳态精度[11].
电导增量法MPPT示意图如图2所示, 图中曲线②斜率dPdU=G+ΔG. 相对于设定值C, 在第一象限和第四象限有交点a、b. 曲线ab之间对应P-U特性有曲线P1、P2点, 即为模糊控制MPPT工作区间,P1点左侧和P2点右侧为电导增量法MPPT工作区间.P1和P2为工作方式切换点.
2 MPPT模糊控制策略
2.1 模糊规则确定
模糊控制负责在最大功率点附近的跟踪. 若输出电压和输出功率的当前采样值和上次采样值, 用n和n-1表示. 在P-U特性曲线上, 最大功率点处dPdU=0, 因此, 在光伏发电MPPT模糊控制中, 输入误差量E及其误差变化量ΔE, 定义如下:
(6)
模糊控制器的输出为V, 用于控制逆变器的逆变角β, 以改变逆变器的输出电压和功率.
模糊控制规则如下:
If dPdU>0, then ΔV>0; If dPdU<0, then ΔV<0; If dPdU=0, then ΔV=0
当dPdU>0时, 表示当前工作点在最大功率点左侧, 需要增加模糊控制器输出量, 即ΔV>0, 以增大逆变器输出电压; 当dPdU<0时, 表示当前工作点在最大功率点右侧, 需要减少模糊控制器输出量, 即ΔV<0; 当dPdU=0时, 表示当前的工作点就是最大功率输出点[13], 不需要改变输出量, 即ΔV=0.
2.2 模糊分级和隶属度函数
为保证模糊控制器的控制性能和精度, 对误差E、 误差变化量ΔE和控制量V, 用七个语言变量分级, 来定义模糊集合[11]: {正大, 正中, 正小, 零, 负小, 负中, 负大}={PB, PM, PS, Z0, NS, NM, NB}. 设工作方式切换设定值C取为0.3. 为保证最大功率点附近的控制精度, 对ΔE的取值按照与E的平方关系进一步细分, 则E和ΔE各等级信号取值, 如表1所示. 定义三角形隶属度函数如图3所示.

表1 各等级信号取值
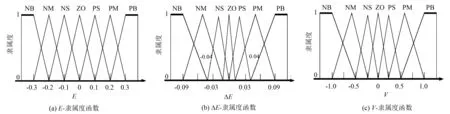
图3 输入输出变量隶属度函数Fig.3 Input and output variable membership function
2.3 模糊控制输出及修正
模糊控制输出分两个步骤实现. 首先, 建立模糊控制规则表, 依据模糊规则和隶属度函数, 由一个输入-输出数据对产生一条规则, 最终生成模糊规则表, 如表2所示.
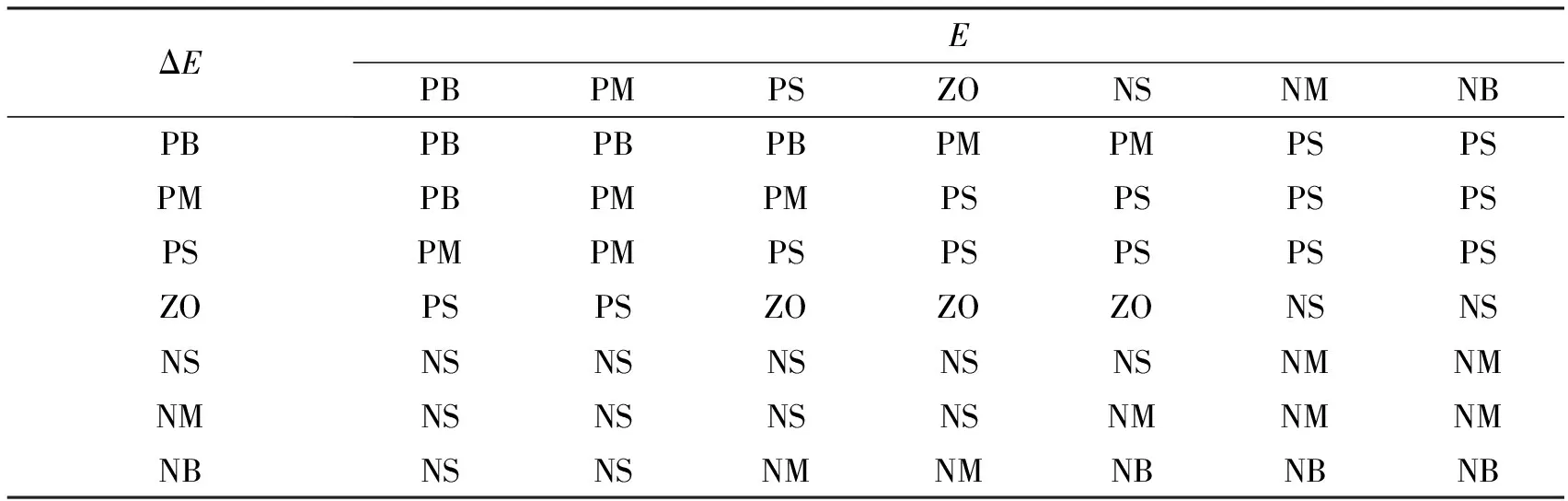
表2 模糊控制规则表(V)
从表2可以看出, 越接近最大功率点时, 控制量逐渐减小, 趋向最大功率点的跟踪. 将规则表进行中心平均律模糊处理, 得到控制量输出值. 将设定值参数C作为修正因子, 对上述控制表进行进一步修正. 将参数C与误差变化量ΔE结合, 叠加到控制输出上. 在距离最大功率点较远时, 误差较大, 控制量输出也较大, 保证系统响应速度. 在接近最大功率点处时, 控制量减少, 以保证控制精度, 使得越接近最大功率点处控制越精细. 其控制解析式为:Vout=(V+C·ΔE).Vout为模糊控制器的最终输出, 对应输出控制的SPWM控制电压, 实现逆变器输出电压控制. 由于参数C可以根据系统参数和运行情况通过人工实时设定, 因此可操作性强, 方便调试. 相对于查表法、 恒定电压法、 最优梯度法、 扰动观察法及常规的电导增量法, 引入修正算法后既能保证系统控制精度又能提高系统快速性. 在实际应用中, 它的选择需要依赖于实际运行参数, 并要经过多次人工测试才能最终确定最佳值.
3 控制效果及验证
3.1 不同光照度下特性曲线
根据以上控制算法, 在Matlab/Simulink平台上构建控制模型进行仿真, 分别改变光照强度和环境温度变化工况下进行分析[11-13]. 设定光伏电池阵列的功率值为300 W, 在20、 30、 40、 50 ms时刻分别改变光照强度为700、 800、 900和1 000 W·m-2, 其仿真曲线如图4所示.
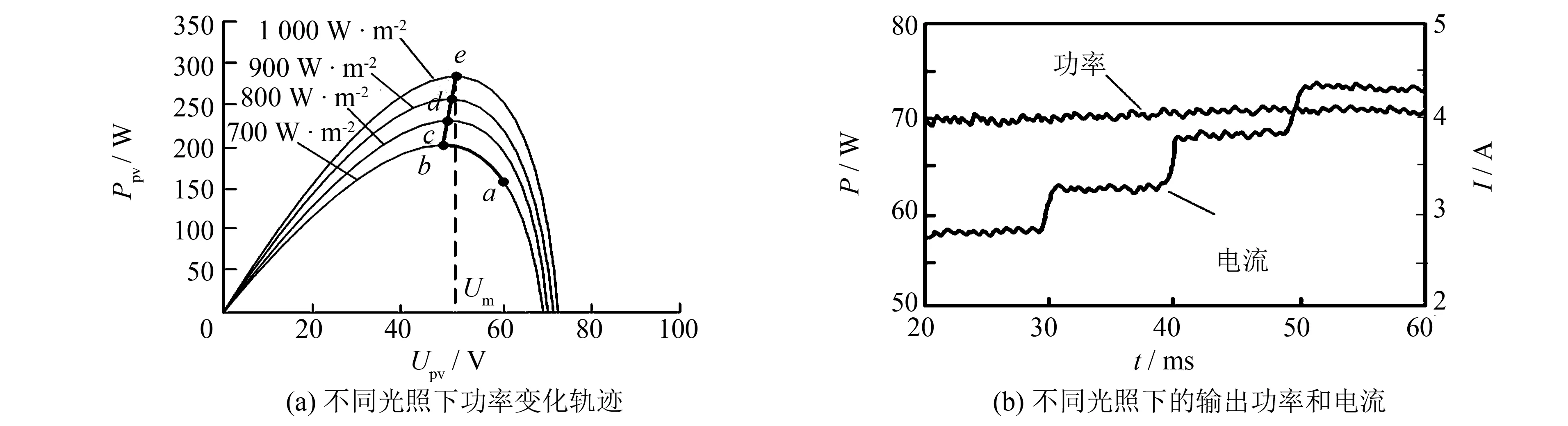
图4 不同光照特性曲线Fig.4 Characteristic curves of different illumination
从P-U过程曲线可以看出, 在不同的光照强度下, 输出功率随光照强度增加而增加, 最大功率点跟踪轨迹为: 起点a→b→c→d→e. 当光照发生变化时, 跟踪轨迹波动小, 可以进行快速跟踪. 随着光照强度变化, 最大功率点的电压Um变化平稳. 输出电流变化明显.P-t和I-t过程曲线与P-U过程曲线吻合, 说明控制效果良好.
3.2 不同环境温度下MPPT曲线
设光照强度为800 W·m-2, 在20 ms时刻开始, 每隔10 ms从20 ℃开始改变温度, 过程为: 20 ℃→0 ℃→-20 ℃→0 ℃→20 ℃→40 ℃→60 ℃[14-15]. 其仿真曲线如图5所示.

图5 不同环境温度特性曲线Fig.5 Characteristic curves of different ambient temperatures
从P-U过程曲线看出, 输出功率随着温度的变化而变化. 相同光强条件下, 温度下降输出功率上升, 反之亦然. 输出电压变化明显, 这主要是因为开路电压Uoc随结温变化明显所致. 输出电流变化不大. 如果实际运行温度没有突变,I-t曲线中的过程曲线将更加平稳.P-t过程曲线和I-t过程曲线的变化与P-U过程曲线相吻合. 说明在温度变化情况下, 最大功率点的跟踪效果良好. 跟踪过程为: 起点a→b→c→d→c→b→e→f.
3.3 MPPT组合算法验证
在某光伏发电站7.2 kW(2.4 kW×3)系统平台同时进行一个季度(2016年4月至6月)的三种MPPT算法控制实验, 以验证电导增量法、 模糊控制算法及本方法与修正因子的模糊控制相结合的组合算法(简称组合算法)三者之间的发电效率. 每组系统采用12块ET-P654200电池板, 每块电池板最大功率为200 W, DSP控制器为TMS320LF2406APZA. 由发电量统计(如表3所示)情形可看出, 对比一个季度的发电量而言, 本组合算法较电导增量法多58.7 kW·h,较模糊控制法多38.4 kW·h. 通过此一实验结果显示本MPPT组合算法确能明显提升光伏发电系统发电效率.

表3三种MPPT算法控制的发电量统计情形

