基于初始信息素和二次挥发的改进蚁群算法

何亮亮,王晓东

(西安工程大学 理学院,陕西 西安 710048)

0 引 言

随着智能计算领域的不断扩大,用于解决优化问题的蚁群算法(ACO)[1]、萤火虫算法(FA)[2]、粒子群算法(PSO)[3]以及蝙蝠算法(BA)[4]等群体智能算法[5]不断涌入,这类算法为解决NP-hard问题提供了较好的方法,其设计原理来源于对大自然中生物行为的效仿．蚁群算法作为最早的仿生物算法,一直备受专家学者关注．近些年,众多学者对蚁群算法进行了深入的研究,解决了旅行商问题[6-7]、指派问题[8]以及调度问题[9]等.目前,针对蚁群算法的改进已有大量的研究,张飞君等[10]提出了一种相遇蚂蚁算法,一次完整的周游路径由2只相遇蚂蚁共同完成,提高了算法运行速度以及扩大了解的搜索空间[10];杨延庆等[11]对信息素最大最小值进行了固定,避免了路径上信息素的差异;HUANG M等[12]针对车辆路径问题引入了3-opt交换策略,初始规划路径得到了进一步的优化;张琦等[13]针对移动机器人路径规划问题,对算法局部启发式函数进行了调整与改进,并且在引入交叉操作的同时调整参数值;姜坤霖等[14]在轮盘赌法的基础上提出了一种新的城市选择策略,并结合提前结束任务的方法减少了算法运行时间;朱颢东等[15]通过选择下一节点转移规则对算法进行了改进,提高了选择最优路径的概率;胡伟[16]将蚁群算法与禁忌搜索算法相结合,改进了蚁群算法的局部搜索能力．这些算法虽然都改善了蚁群算法的缺点,但对初始信息素分布的改进以及信息素的二次挥发的研究还较少．由于基本蚁群算法中的初始信息素浓度为定值,蚂蚁选择下一节点时仅依靠路径的长度,而信息素的挥发发生在每条路径上,降低了算法的寻优效率,因此结果不一定最优;另外,随着迭代次数的增加,后期路径信息素残余量较少,算法的寻优能力也相应减弱．为了改善以上2种状况,本文对蚁群算法初始信息素的分布以及信息素的挥发因子进行改进,提高了算法的收敛速度和后期的寻优能力．

1 基本蚁群算法

蚁群算法是学者从蚂蚁觅食过程受到启示得来的一种仿生物算法．研究者发现蚂蚁会在路径上释放一种信息素的激素,它会随着时间逐渐挥发,之后的蚂蚁可以感觉到信息素的存在,并且沿信息素浓度较高的路径前进，同时继续释放信息素,这样越来越多的蚂蚁会聚集到一条路径上,从而形成了正反馈机制．蚂蚁根据式(1)选择未被访问的下一个城市,并将其添加到禁忌列表．

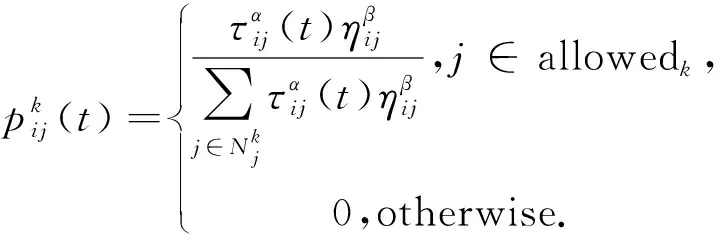
(1)

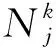
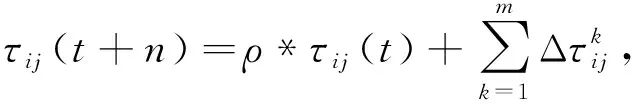
(2)

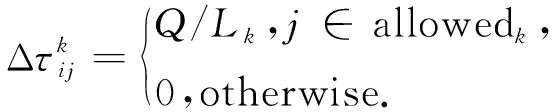
(3)

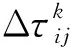
2 蚁群算法改进

2.1 初始化信息素改进

在基本蚁群算法中,设m为蚂蚁个数,n为城市数目,刚开始时的信息素量为m/cm,其中cm是由最邻近方法构造出来的路径的长度．在算法初始阶段,信息素浓度小,蚂蚁可觉察到信息素的能力相对较弱,需要经过一段时间的摸索,才能找出一条相对较优路径．在这个过程中耗费了大量的时间,降低了算法的收敛速度．为了改善这种状况,考虑通过路径距离重新设定初始信息素的分布,使得算法有方向地进行搜索,以克服搜索的盲目性．对初始信息素改进如下:

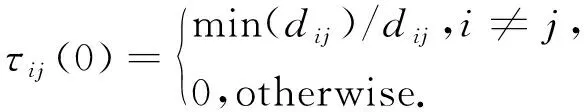
(4)

式中:dij为蚂蚁所在城市i到城市j之间所有可能的距离,min(dij)为所有可能距离中最短路径距离．由于城市坐标位置固定,所以全局最小距离min(dij)不变,蚂蚁所选择的路径dij越短,初始信息素就越大,且蚂蚁是在权衡全局路径距离dij与最短路径min(dij)的比重之后选择路径,从而使得算法避免盲目搜索,节省了大量的时间．

2.2 信息素挥发因子

在基本蚁群算法中,信息素的更新仅对较优路径上的信息素进行更新,然而最优路径的子路径并不总是最短路径,同时可能存在较长路径,这样会导致蚂蚁从一开始就选错路径,也就错过了最优路径．为了解决这一缺陷,文献[17]引入了路径贡献度，见式(5).在最优路径中,找出对整体路径贡献度大于路径贡献度阈值的子路径．并按式(6),(7)对这条子路径上的信息素进行二次更新：

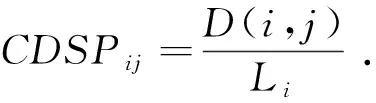
(5)

(6)

(7)

在基本蚁群算法中,信息素挥发因子为定值．由于每次迭代得到的较差解对最终结果没有帮助,如果信息素的挥发在较差路径上相对较慢,则残留的信息素越多,就会影响算法寻找最优解的速度,因此应减慢较优路径信息素挥发的速度,加快较差路径上的信息素挥发速度,所以针对文献[17]中信息素的二次更新后的信息素考虑进行二次挥发,使得二次挥发系数与迭代次数平方成反比．随着迭代次数的增加,挥发因子相应减小,算法后期未走路径上信息素挥发速度相应减慢,蚂蚁感知到的信息素则相应增多,一定程度上改善了算法后期寻优能力弱的缺陷．因此对二次挥发因子改进为

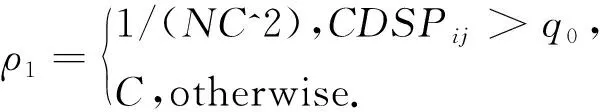
(8)

式中：C为以常数;NC表示算法的迭代次数;CDSP为路径贡献度;q0为路径贡献阈值(取常数)．信息素按照式(9)进行更新:

τij(t+n)=(1-ρ)τij(t+n)+ρ1τij(new).

(9)

3 改进的蚁群算法步骤

Step 1:初始化蚁群算法中的参数m,α,β,η,ρ,q0、NC-max,NC=1,计算城市间的距离dij,初始信息素τij(0)按照式(4)取值;

Step 2:将m只蚂蚁放置n个城市中作为起点,为每只蚂蚁建立禁忌表tabu,计算启发因子;

Step 3:按照式(1)选择下一个要访问的城市j,当蚂蚁到达城市j后,将j加入到禁忌表tabu中;

Step 4:若禁忌表tabu未满,则跳转至Step 3;若tabu已满,则输出本次迭代最优长度Length-best及最优路径Route-best;

Step 5:根据全局更新规则,按式(2),(3)对信息素进行首次更新;

Step 6:按式(5)计算路径贡献度;按式(6),(7)计算新的信息素变化量Δτij(new);按式(8)得出二次挥发因子ρ1;根据全局更新规则,按式(9)对信息素进行二次更新;

Step 7:若满足迭代条件NC≥NC-max,则输出最优长度Length-best;若不满足条件,则NC=NC+1,返回Step 2．

4 仿真实验与分析

为了验证改进蚁群算法的有效性,将基本蚁群算法与改进后的算法通过TSPLIB中的4组数据Eil51、31个城市、Oliver30和Att48分别进行寻优搜索对比．运行环境为Windows 10系统、Matlab 2016a软件．2种算法的公共参数:m=50,α=6,η=7,ρ=0.1,q0=0.4．在此参数下每组数据各运行20次,运行结果见表1,改进前后蚁群算法对比如图1，2所示.表1中最优解和最差解分别为运行20次后2种算法搜索到的最优解中最好的1次和最差的1次,平均解表示运行20次后2种算法搜索到的最优解平均值．

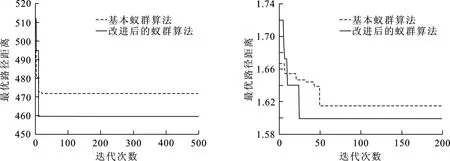
(a) Eil51迭代图 (b) 31个城市迭代图图 1 改进前后蚁群算法对比Fig.1 Comparison of ant colony algorithm before and after improvement

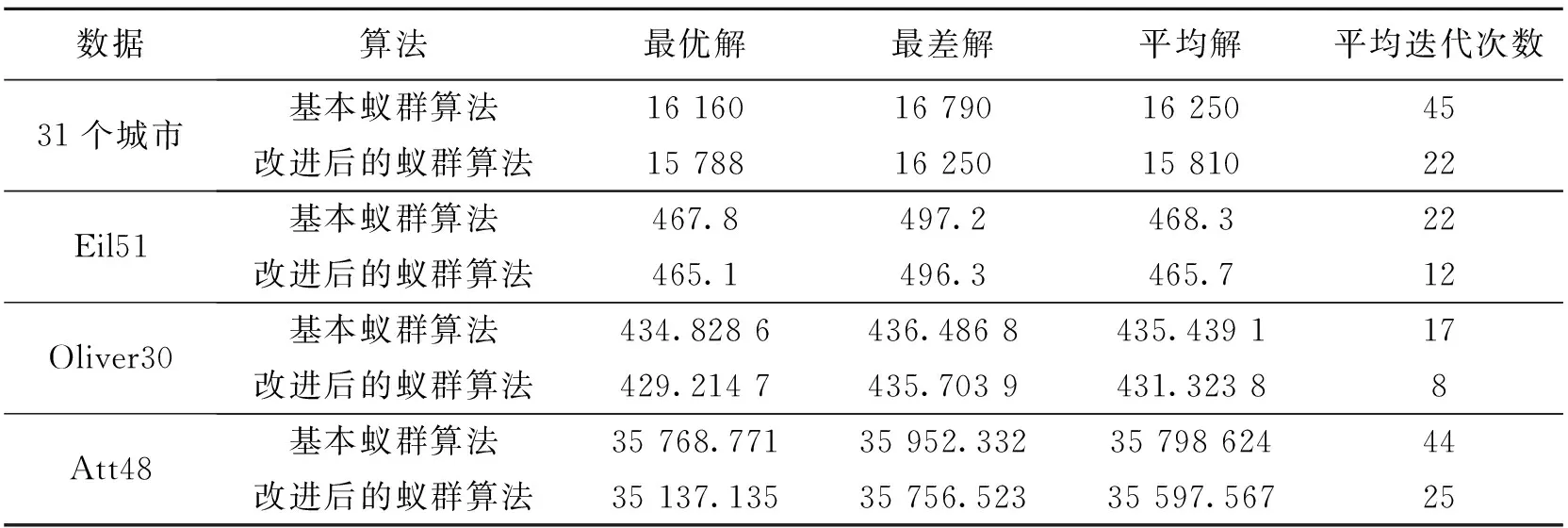
数据算法最优解最差解平均解平均迭代次数 31个城市基本蚁群算法16 16016 79016 25045改进后的蚁群算法15 78816 25015 81022 Eil51基本蚁群算法467.8497.2468.322 改进后的蚁群算法465.1496.3465.712 Oliver30基本蚁群算法434.828 6436.486 8435.439 117 改进后的蚁群算法429.214 7435.703 9431.323 88 Att48基本蚁群算法35 768.77135 952.33235 798 62444 改进后的蚁群算法35 137.13535 756.52335 597.56725

从表1可以看出,在31个城市数据下,基本蚁群算法得到最优解为16 160,而改进后的蚁群算法的最优解为15 788,最优解减少了372,最差解的差值为540,平均解提升了440;在Oliver30数据下,基本蚁群算法所得到最优解为434.828 6,而改进后的蚁群算法的最优解为429.214 7,最优解减少了5.613 9,最差解的差值为0.782 9,平均解提升了4.115 3;其余2组数据的最优解和平均解比改进前更优,改进后的蚁群算法寻优能力更强;从平均迭代次数上看,31个城市数据下迭代次数缩减了23次;Eil51数据下迭代次数缩减了10次;Oliver30数据下迭代次数缩减了9次;Att48数据下迭代次数缩减了19次．4组数据改进前后的迭代次数均有明显的减少,改进后的蚁群算法收敛速度更快．

2种算法对Eil51和31个城市的20次搜索最优值中其中的一次迭代对比如图1所示．从图1(a)可以看出，基本蚁群算法的最优解大于470,而改进后的最优解小于460;从图1(b)图中可以看出，基本蚁群算法最优解大于16 100,而改进后的最优解明显小于16 000;并且达到最优解时,改进后的蚁群算法迭代曲线的拐点均在基本蚁群算法迭代曲线拐点前,说明改进后的蚁群算法较基本蚁群算法优先跳出局部最优．

31个城市下蚁群算法优化路径如图2所示．从图2(a)可以看出,在中国的31个城市数据下的基本蚁群算法最优解为16 148.379 8,最优路线为27,28,26,25,24,20,21,22,18,3,17,19,23,11,12,14,13,7,6,5,16,4,2,8,9,10,15,1,29,30,31．从图2(b)可以看出，在中国的31个城市数据下的改进蚁群算法的最优解为15 989.982 1,最优路线为:1,15,13,12,14, 11,23,16,5,6,7,2,4,8,9,10,3,18,17,19,24,25,20,21,22,26,28,27,30,31,29,1．

(a) 基本蚁群算法路径 (b) 改进的蚁群算法路径图 2 蚁群算法优化路径Fig.2 Ant colony optimization path

5 结 论

(1) 在基本蚁群算法的基础上,对初始信息素改进,在文献[17]的基础上建立了二次信息素挥发因子,并通过MATLAB软件在相同的参数条件下,对改进的蚁群算法和基本蚁群算法进行仿真.

(2) 改进的蚁群算法不但继承了算法本身的优良性,而且弥补了基本蚁群算法效率低、“早熟”以及后期寻优能力差等缺点,改进的蚁群算法有效可行．