基于Hadoop的Canopy-K-means并行算法的学生成绩与毕业流向关系分析

郭卫霞,薛 涛,李 婷

(西安工程大学 计算机科学学院,陕西 西安 710048)

0 引 言

随着高校智能化、信息化建设的推进,大量的学生信息被存储在教务系统中.近年来,越来越多的高校开始关注学生的毕业流向与学生成绩之间存在的关系,希望能够通过分析其内在关系建立模型,通过学生的成绩预测出其可能的毕业流向.对于教务系统中存储的学生数据,虽然这些数据具有海量、杂乱、冗余等特点,但是分析数据之间存在的关联性和相似性[1]，对这些数据进行清洗、挖掘和分析,可以帮助教务人员更好地了解学生未来可能的毕业流向,对学生进行更好的教育引导.

目前,已有很多高校在教务数据分析领域做出了一些研究.龙松等[2]针对已毕业学生的在校学习成绩和毕业去向等信息,利用判别分析建立费歇尔判别函数,对即将毕业的学生的就业去向进行预测;林秀科等[3]运用决策树分类算法对学生成绩综合分析,挖掘出对学生毕业产生影响的关键课程;陈甲华[4]通过分析学生成绩数据运用改进后的Apriori算法建立了大学成绩关联规则分析模型;韩霖[5-6]等研究了影响大学生就业的因素，并基于遗传算法的神经网络模型建立了数学模型.研究教务数据间的内在关系具有重要意义,例如可以通过对往届学生的学科成绩和毕业流向进行分析,发掘之间存在的关联,预测学生的毕业情况,帮助广大毕业生更好地实现就业.

目前大部分高校对于校务研究中学生成绩信息的综合分析和挖掘还明显不够,本文以西安工程大学2017届学生四年的成绩为依据,分析其和毕业流向之间的关系.针对大量的学生成绩与其毕业流向的数据,给出一种基于Hadoop[7-8]的Canopy-K-means并行算法.Canopy-K-means算法解决了传统K-means算法初始簇中心选择敏感的问题,提高了算法聚类的准确度,基于MapReduce[9-10]编程模型实现其并行化,提高算法执行效率.

1 模型架构

本文采用Hadoop云计算主/从(Master/Slave)架构实现海量教务数据的存储和分布式计算[11],通过数据挖掘算法实现对数据中潜在的有价值信息的挖掘分析,发现数据间存在的内在关系并进行分析预测等，图1为基于Hadoop的教务数据分析模型架构.

如图1所示,数据源端将预处理后的学生成绩及其毕业流向数据上传至Master.Master一方面要对源数据进行业务模型转换和业务数据抽取,提取有价值的维度建立数据维度模型;另一方面,Master还要对数据进行挖掘分析和业务趋势预测,建立数据挖掘模型.数据管理模块依据数据维度模型将数据分块存储到各Slave上并记录其存储位置,同时Master还要管理各Slave相应任务的执行.

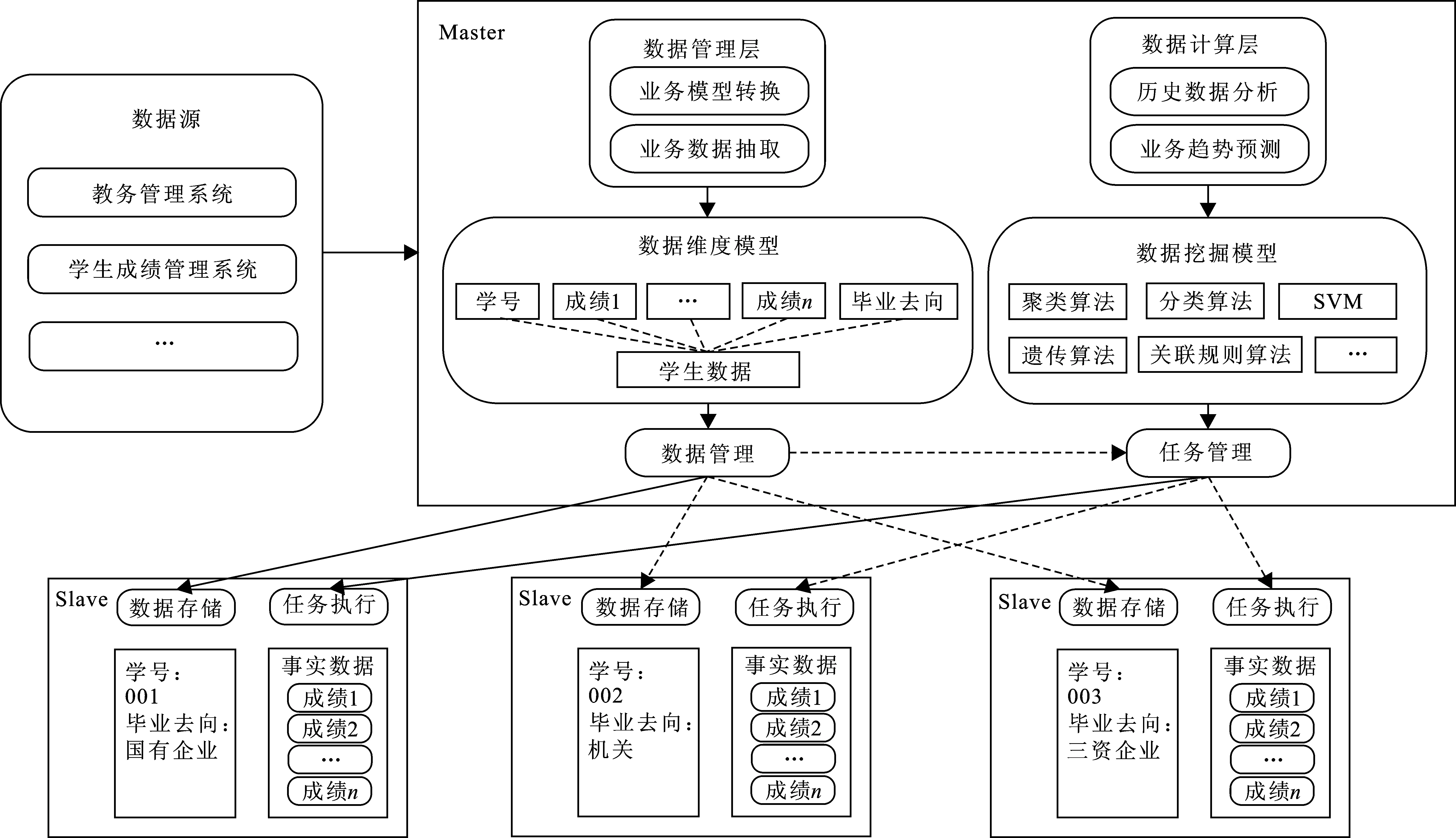
图 1 基于Hadoop的教务数据分析模型架构Fig.1 The architecture of educational data analysis based on Hadoop

主节点收到分析请求,会根据任务种类的不同选取不同数据挖掘算法,Master节点将维度分解后的任务分配给各从节点,Slave接收到分配的任务之后,各节点从HDFS[12]中读取数据进行并行化的子任务处理,配合主节点选择的挖掘算法执行数据分析任务,从而实现海量数据的分析,快速、高效地获取数据中有价值的信息.

2 教务数据分析

2.1 传统K-means算法

K-means是一种较为经典的基于划分的聚类挖掘算法[13-14],该算法快速简单、易于实现,具有良好的可伸缩性,被广泛应用于文本分类、文本分析[15-16]等领域.

设数据集集合D={x1,x2,…,xn},xi=(xi1,xi2,…,xin),xj=(xj1,xj2,…,xjn),

则样本xi与样本xj之间的欧氏距离为

全局误差函数(本文选其作为有效性函数)为

式中:E为误差;k为聚类中心个数;Si为k个类中的一个;ui是Si的中心;xj是Si中的任意元素.

传统K-means算法中,对于初始簇中心的选择是随机的,这种随机性容易在迭代中形成大量冗余,使聚类结果陷入局部最优,造成聚类效果不理想等问题.为了解决传统K-means算法对于初始簇中心选择的盲目性问题,提高聚类质量,给出了一种Canopy-K-means改进算法.

2.2 改进后的Canopy-K-means算法

Canopy-K-means算法的主要思想就是预先通过Canopy算法对原始数据集进行粗糙聚类,快速得到k个Canopy中心和k个可以相互重叠的Canopy,然后将其作为下一步K-means算法的初始聚类中心,对同一Canopy内的数据进行精确聚类,直到得到稳定的簇类中心.Canopy之间的可重叠性能够达到消除孤立点的作用,提高算法的容错性;预先给K-means算法指定初始簇中心,可减少计算量,加快算法收敛速度,提高聚类结果的准确性.

Canopy算法过程如下:

(1) 设置2个区域半径t1,t2且满足t1>t2;

(2) 首先从数据集中随机选取1个数据点作为Canopy的中心点,遍历整个数据集,将与该中心点之间的距离小于或等于t1的数据点归入此Canopy中;

(3) 若距离小于t2,则把该数据点从原始数据集中剔除,直到整个数据集为空.

由以上过程可知,Canopy算法的执行效率受最初设置的2个区域半径t1,t2影响较大,当t1过大时,会使同1个数据点属于多个Canopy,加大了聚类过程中的计算开销;当t2过大时,会使得最终聚类的个数较少,可能会使整个聚类过程陷入局部最优[17].

为了避免聚类过程陷入局部最优,应该将Canopy算法的初始中心点之间的距离设置得尽可能远一些[18].本文采用“最小最大原则”[19]来改进Canopy算法,确定Canopy聚类的初始中心点.其基本思想如下:

(1) 首先在数据集C={x1,x2,…,xi}中随机选择一个点作为第1个中心点xA;

(2) 计算数据集中其余数据点到xA的最小距离,从中选取距离最大的点作为第2个中心点xB;

(3) 继续计算数据集中其余数据点到xA,xB的最小距离min{d(xi,xj),j=A,B},选取这些最小距离中的最大者max{min[d(xi,xj)],j=A,B}作为第3个中心点xC.

以此类推,最终所有的Canopy初始中心点{xA,xB,…,xK}应满足:

其中min[d(xi,xj)]表示数据集中其余各点与已确定的前K-1个Canopy中心点的最小距离的集合,Distmin(xK)则表示待确定的第K个Canopy中心点xK距已确定的前K-1个Canopy中心点的距离应为所有最短距离中的最大者.

运用“最小最大原则”的方法选取Canopy中心点,可以有效避免Canopy参数t2的设置[18].根据上述方法,在MapReduce进行数据分析时可归约为:Canopy粗聚类结果类别数少于或超过类别真实值时,Distmin(xK)小幅度变化;当 Canopy粗聚类结果类别数接近类别真实值时,该距离变化幅度较大[18,20].因此,为了确定Canopy中心点的最优个数以及区域半径t1,参照文献[21]中的边界识别思想,引入了表示Dist(xK)变化幅度的深度指标Depth(i),其定义为

Depth(i)=|Distmin(i)-Distmin(i-1)|+|Distmin(i+1)-Distmin(i)|.

当i达到最优聚类时,Depth(i)取值最大,那么最优的初始聚类中心点即为Canopy集合中的前i个点,同时设置区域半径t1=Distmin(i),从而确保目前聚类中心点最终均能落在Canopy范围内.

基于“最小最大原则”改进的Canopy算法不仅解决了盲目设置Canopy参数t1,t2的问题,而且使传统选取Canopy中心点的问题得以改善,以便得到更稳定的Canopy聚类中心点集合,为K-means提供有效、精准的聚类中心,使聚类结果更加精确.

图2为Canopy聚类结果示意图,实线圆圈为Canopy算法粗糙聚类后生成的可相互重叠的Canopy,虚线圆圈表示其最终所属的簇.由图2可以发现通过Canopy算法预先聚类后,任意2个不属于同一个Canopy的数据点最终不可能属于同一个簇[22].因此K-means精确聚类时则不必计算不处于同一个Canopy的数据点之间的距离.如簇A、C、D都只属于一个Canopy,而簇B、E则属于2个Canopy.点x、y均被2个Canopy包括,则在K-means精确聚类时,只需计算点x、y分别到这2个包含它们的Canopy中心的距离,即可完成划分,确定其最终所属的簇.

图 2 Canopy聚类结果示意图Fig.2 The diagram of Canopy clustering result

2.3 教务数据挖掘

在MapReduce编程框架下,Canopy-K-means算法的并行化实现划分为若干Job,执行流程如图3所示.

图 3 Canopy-K-means并行算法的数据挖掘执行流程Fig.3 Data mining execution process of Canopy-K-means parallel algorithm

Canopy-K-means并行算法的MapReduce计算步骤如下:

(1) 将存储在HDFS上的教务数据按行分片处理,并发送给n个待执行Map任务的节点;

(2) 每个Mapper输入一个键值对,其中key为学生学号StuID,value为各科成绩及其毕业去向StuInfo,即.每个Mapper针对自己所需处理的数据集,利用“最小最大原则”确定Canopy中心点,输出键值为Canopy编号,value为Canopy中心点;

(3) Reducer接收Mapper的输出值,将key值相同的Canopy进行合并,重新计算Canopy中心点,得到全局的Canopy中心点;

(4) 将n个Canopy分别发送给n个Mapper作为分片数据,将已经得到的Canopy中心点作为K-means聚类的初始簇中心,用K-means算法对每个Canopy中的数据进行精确聚类,输出key为簇编号,value为簇中心点;

(5) Combiner接收Mapper的输出值,将key值相同的簇进行合并且输出给Reducer;

(6) Reducer更新每一个簇中心，最终得到全局的簇中心,并将教务数据划分至每一个簇中;

(7) 此时判断有效性函数是否达到阈值,若没有达到阈值迭代步骤4～6,反之则输出最终K个簇的信息作为聚类的最终结果,至此聚类过程结束.

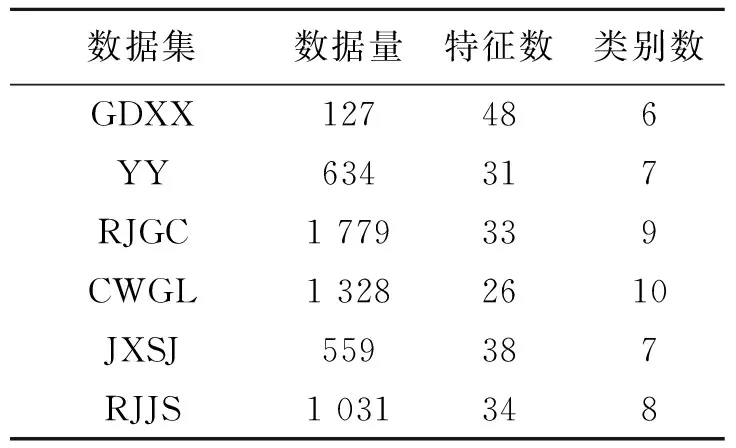
表 1 教务数据集相关参数Table 1 Related parameters of educational data set

3 实验设计与结果分析

3.1 实验环境与实验数据

实验环境:实验使用Ubuntu 16.04.3作为系统环境,JDK版本为1.8.0_161,搭建了基于Apache Hadoop 2.6.5的4个节点的集群,包括1个Master节点和3个Slave节点.

实验数据为西安工程大学2017届毕业生四年的学习成绩及其毕业流向情况.数据集相关参数如表1所示.

3.2 结果分析

3.2.1 性能验证实验 为了验证改进后的Canopy-K-means算法的有效性,选用教务数据的部分数据集,分别采用传统K-means算法和改进后的Canopy-K-means算法进行对比实验,通过聚类准确率参数进行衡量比较.

如图4所示,改进后的Canopy-K-means算法的聚类准确率可提高约14%.聚类结果的参数表明,改进后的Canopy-K-means算法具有更好的聚类效果.

3.2.2 单机集群对比实验 为了验证MapReduce并行模式下对于海量数据的处理效率,选用改进后的Canopy-K-means算法,针对教务数据的部分数据集,分别进行单机模式下和MapReduce并行模式下1～4个节点的数据聚类实验,并计算聚类收敛时间.

单机模式和MapReduce并行模式下的聚类收敛时间对比如图5所示.由图5可知,当数据规模较小时,MapReduce多节点模式下和单机模式相比,收敛时间没有明显的缩短.这是由于数据量较小时聚类时间较短,Hadoop在并行节点的任务启动和分配上需要花费一定的时间,因而并没有体现出并行处理的高效性;当数据量达到一定规模时, MapReduce模式下多节点并行处理数据的效率明显优于单机模式,并且节点数越多,聚类效率越高.数据量较大时,MapReduce 多节点模式下相比单机模式收敛速度提高约2.1倍.另外,可以发现随着节点数的增加,算法处理数据的速度的增长率逐渐变缓,这是因为Hadoop平台上的节点数越多,节点间的通信时间花费越大.综上,本文采用的并行挖掘算法对于处理海量教务数据在速度方面有所提高.

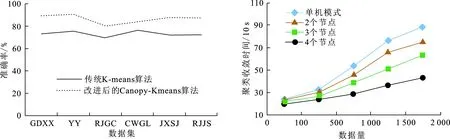
图 4 K-means算法改进前后收敛时间对比 图 5 单机和MapReduce并行模式下聚类聚类效果 Fig.4 K-means algorithm clustering effect on before and after Fig.5 Comparison of cluster convergence time with stand-alone and MapReduce parallel mode

3.2.3 教务数据聚类分析实验 基于Hadoop平台和改进后的Canopy-K-means算法,针对教务数据集完成聚类任务.根据数据预处理后得到的学生信息特征向量,将毕业去向相似的学生进行聚类,同时得出该院学生的毕业流向分布情况以及每类学生的成绩水平曲线.

以RJGC数据集为例,该院学生的毕业流向分布情况如图6所示,由聚类结果可知该院学生就业情况良好,读研、进入外企和私企的学生占大多数.

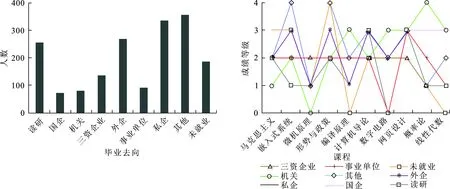
图 6 RJGC学院学生毕业去向分布情况 图 7 各类学生成绩水平曲线 Fig.6 RJGC College students graduate distribution Fig.7 Various students′ performance level curve

不同毕业流向的学生成绩水平曲线如图7所示.以RJGC数据集为例,根据毕业流向学生最终分为九类.图中成绩等级0～4分别代表优、良、中、及格、不及格,暂定学生的毕业流向与成绩为良及以上的课程关系较密切,此处选取3门作为最终与该毕业流向关联最为密切的课程,如果某毕业去向的相关课程中成绩为良及以上的课程较多或者不足3门时,按课程成绩由高到低选取前3门作为最终结果.由此进行简单统计分析可得出,RJGC学院的学生毕业流向为国有企业时,与马克思主义基本原理、计算机科学导论和微机原理与接口技术这3门课程关系较密切;毕业流向为机关时,与嵌入式系统软件设计、微机原理和形势与政策等课程关系较密切;未就业的同学大多为网页设计、编译原理及计算机科学导论等课程基础较为不扎实.

根据图7的分析结果,教务人员可以根据学生对未来从事工作的打算对学生进行更好的教育引导,并对一些对毕业流向影响较大的课程加以重视.当然,由于初始数据维度较高,缺省数据较多,实验结果存在一定的误差性及不稳定性.

4 结束语

本文以海量教务数据为基础,采用基于Hadoop的Canopy-K-means并行算法,研究了学生成绩与毕业流向之间的内在关系.首先,对于传统K-means聚类算法存在的确定初始聚类中心的随机性问题,利用基于“最小最大原则”的Canopy算法快速获取聚类中心,将其作为K-means算法的初始聚类中心,可大大减少计算量,相比传统K-means算法,聚类收敛时间缩短约2.1倍,准确率提高约15%.

其次,采用基于Hadoop的Canopy-K-means并行算法对教务数据进行分析研究.通过对学生成绩及其毕业流向数据的预处理,提取学生必修课程成绩及其毕业去向等特征,建立数据向量维度,然后用改进后的Canopy-K-means算法对数据进行聚类分析,并以MapReduce模型实现算法的并行化,最后对聚类结果进行分析,提取每一类学生成绩的特征.挖掘教务数据中有价值的信息,分析学生毕业流向与其必修课程成绩之间的关系,对教务人员预测学生未来的毕业流向,更好地教育引导学生具有重要的指导意义.

在下一步的工作中,将增加实验对象的涉及面,多层次多角度地进行关联分析,多维地考虑影响学生毕业流向的相关因素,对算法模型做进一步的优化,并结合分析模型的聚类结果,通过学生成绩对其未来的毕业流向进行预测.