基于自适应平方变换的工件去噪方法

刘秀平,薛婷婷,徐 健,张凯兵,杜勇辰

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

随着机器学习和人工智能的迅速发展,图像处理在医学成像、模式识别等方面有广泛的应用．工件图像在获取和传输过程中,会掺杂一定的噪声成分.有些噪声与信号混杂在一起,使得工件图像本身的细节模糊不清,影响后续图像处理．因此,去除工件图像噪声成为图像处理的关键步骤．

常用的图像去噪方法有基于空域、基于频域和基于稀疏表示．基于空域滤波是在原图像上直接进行数据运算[1],对像素的灰度值进行处理，去噪速度快,但易滤除图像的细节部分,造成图像边缘信息模糊；基于频域滤波是将图像变换到频域处理后再变换到空域的去噪方法[2]，该方法可以处理某些空域中无法去除的噪声,但无法完全去除噪声,且选取不合适的阈值也会造成边缘模糊和细节丢失等现象；基于稀疏表示的方法是将图像中的有用信息作为图像的稀疏部分[3],残差作为图像的噪声,从而实现图像降噪．基于稀疏表示去噪的方法主要包括基于字典的表示方法和基于学习的表示方法．在字典的表示方法中,字典的数学表达式已知,如轮廓波(contourlet)变换[4]、曲波(curvelets)变换[5]、带状波(bandlet)变换[6]等．这些变换计算速度快,但对图像的几何特征过于依赖,对于几何特征较多的图像,固定的字典处理效果较差．基于学习的表示方法,通过训练获得字典,再采用正交匹配算法和基追踪算法对数据进行处理．如K-SVD[7],核特征值分解(K-EVD,kernel eigen value decomposition)[8],核模糊代码本估计(K-FCE,kernel fuzzy codebook estimation)[9],该类算法的计算复杂度高,对大数据的图像处理效果较差．近年来,一些学者[10-11]提出了在线稀疏变换学习理论,并在信号处理中有较好的应用;文献[12]提出了稀疏变换学习算法的理论知识,并证明其收敛; 在此基础上,文献[13-14]进一步完善该算法,并将其应用于信号处理中．

本文给出了一种基于自适应平方变换的方法对不同光源下的工件图像进行去噪研究,该方法首先从噪声图像中提取噪声图像块,接着通过学习平方变换和更新平方变换水平得到去噪性能较好的去噪块,最后利用图像中各自位置的去噪块估计去噪图像．

1 各种光源特点

光源对图像处理有非常重要的影响[15]．本文对环形白光源(RWLS,ring white light source)、环形红光源(RRLS,ring red light source)、圆顶光源(DLS,dome light source)、面光源(ALS, area light source)、条形光源(SS,strip source)和同轴光源(CLS,coaxial light source)等6种光源下采集到的工件图像进行实验研究．RWLS的光线均匀扩散,在低角度照射下能突出被检测物体的边缘和轮廓,可以有效解决对角照射阴影问题,常用于外形尺寸的测量,边缘破损检测;RRLS的红光容易透射,可增加图像的对比度,有利于凸显图像的细节信息;DLS的光扩散面大,对物体照射均匀、平滑,可消除表面凹凸不平物体的阴影,对表面反射性强且有复杂角度目标的物体有较好的检测;ALS发光均匀、稳定,可产生无影效果,对于反光物体可削弱反光现象,能充分突出被测物体的轮廓信息,通常用于外形轮廓检测；SS安装灵活方便，照射光线稳定，但均匀性不好，且易反光;CLS的光强度高,分布均匀,可消除采集图像的重影,该照明方式特别适合检测高反射以及受周围环境影响产生阴影面积不明显的物体．

2 自适应平方变换去噪

2.1 平方变换模型

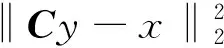
2.2 学习平方变换

给定一个矩阵Y∈Rn×N,平方变换学习定义为[12]

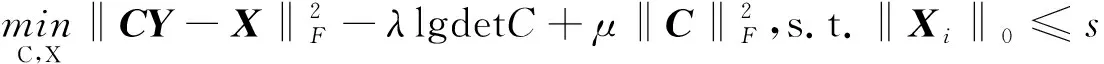
(1)

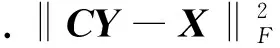
(1) 稀疏编码更新 固定C,求解X,即

(2)

通过变换CY可以精确地计算稀疏编码X,并且保留每列的最大稀疏系数s．

(2) 平方变换更新 固定X,求解C,即

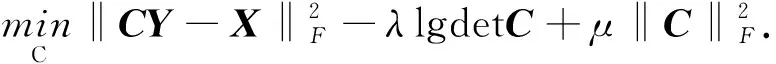
(3)

运用迭代方法，如最速下降法或梯度共轭算法(CG)可以解决式(3)问题[12]．

2.3 自适应平方变换去噪

去噪的目的是从有噪声e的二维图像的测量值y=x+e中恢复一个二维图像的估计值,该估计值表示为向量x∈RP．基于平方变换学习算法的去噪公式可表示为

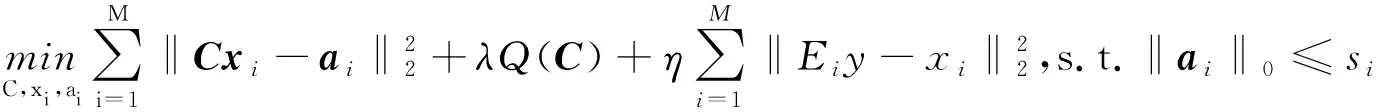
(4)

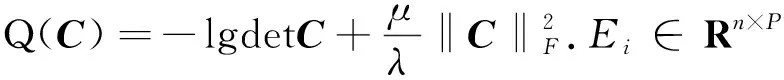
图 1 自适应平方变换去噪Fig.1 The denoising chart of adaptive square transform

用给定的变换C对噪声块去噪,该变换C从噪声图像块中学习．式(4)的求解步骤如下:

(1) 平方变换学习 固定xi=Eiy,si=s(s为初始值),利用平方变换学习求解C．从噪声图像中提取噪声图像块Eiy减去该块的均值;然后固定噪声图像块的稀疏水平si,从噪声图像块中学习平方变换C;

(2) 更新稀疏水平 固定C和αi,更新所有i对应的稀疏水平si,式(4)简化为一个最小二乘问题,通过单独更新每个xi求解为

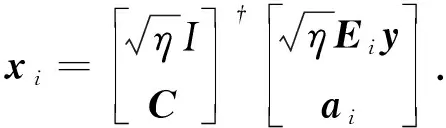
(5)

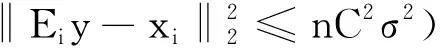
3 结果与分析

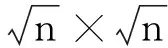
3.1 去噪性能分析

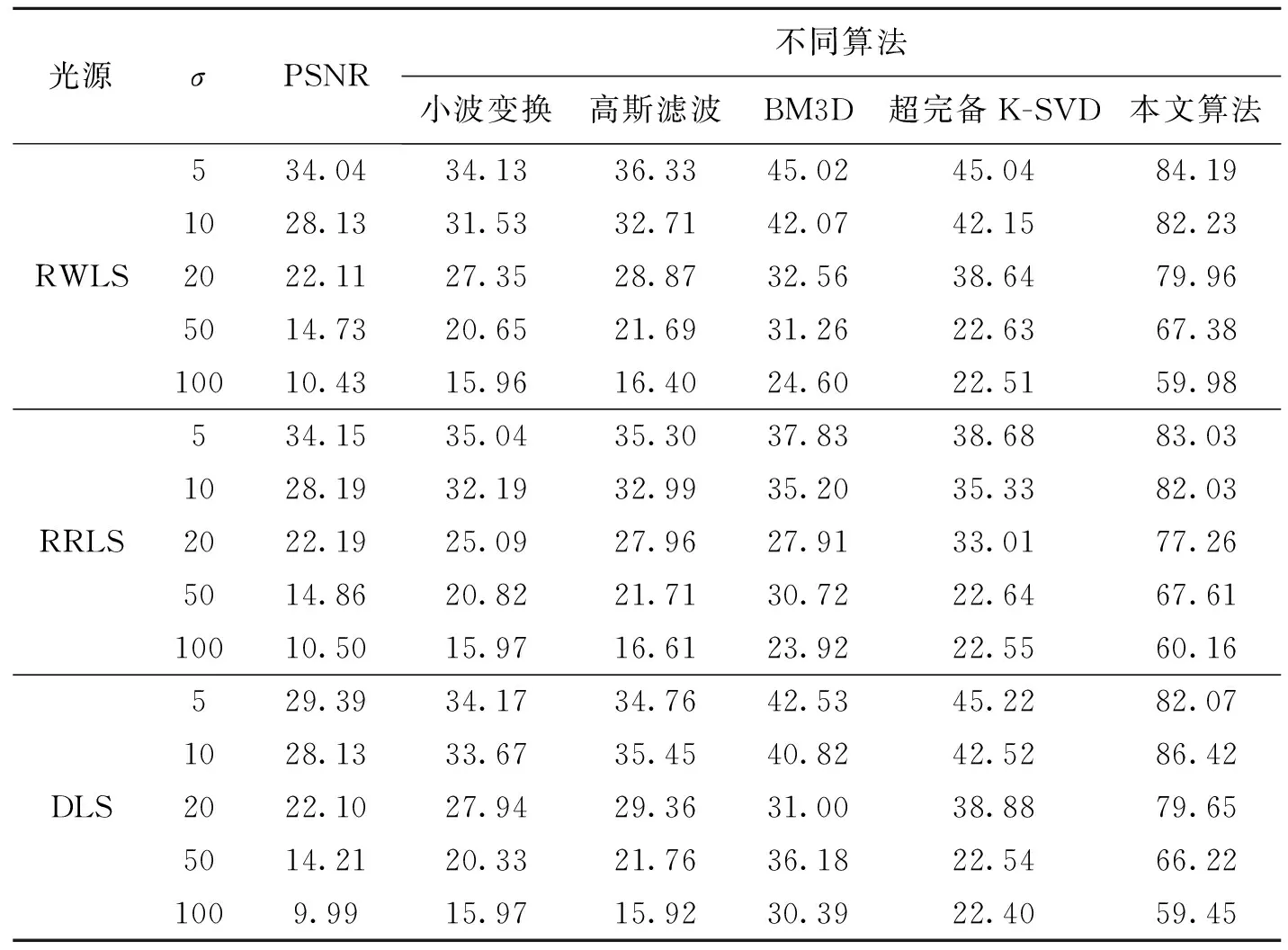
为了比较噪声对工件图像去噪效果的影响,对6种光源下采集到的不规则工件图像添加不同的高斯噪声(σ=5,10,20,50,100)进行实验,与小波变换、高斯滤波、BM3D算法[20]和超完备K-SVD算法[21]比较.从表1可以看出,各种算法去噪后的PSNR值增加,且本文算法去噪后的PSNR值约是传统稀疏变换(小波变换和超完备K-SVD)的2倍．在6种光源中,随着噪声水平的增加(σ=50和σ=100),BM3D算法去噪后的PSNR值略大于超完备K-SVD算法(表中加粗数据)．由于BM3D算法的非局部性,使其去噪性能较好．而本文算法去噪效果明显高于上述4种算法,本文算法对图像进行分块处理并将其转换到变换域,在变换域中通过图像块学习到自适应的稀疏字典,该字典可以有效地表示图像中噪声信息的特征．通过该稀疏字典可以得到较好的稀疏编码,从而得到去噪效果较好的去噪图像．

表1 6种光源中不同噪声水平去噪的PSNR值

Table 1 The PSNR of different noise levels under 6 light sources dB

光源σPSNR不同算法小波变换高斯滤波BM3D超完备K-SVD本文算法534.0434.1336.3345.0245.0484.19 1028.1331.5332.7142.0742.1582.23 RWLS2022.1127.3528.8732.5638.6479.96 5014.7320.6521.6931.2622.6367.38 10010.4315.9616.4024.6022.5159.98 534.1535.0435.3037.8338.6883.03 1028.1932.1932.9935.2035.3382.03 RRLS2022.1925.0927.9627.9133.0177.26 5014.8620.8221.7130.7222.6467.61 10010.5015.9716.6123.9222.5560.16 529.3934.1734.7642.5345.2282.07 1028.1333.6735.4540.8242.5286.42 DLS2022.1027.9429.3631.0038.8879.65 5014.2120.3321.7636.1822.5466.22 1009.9915.9715.9230.3922.4059.45

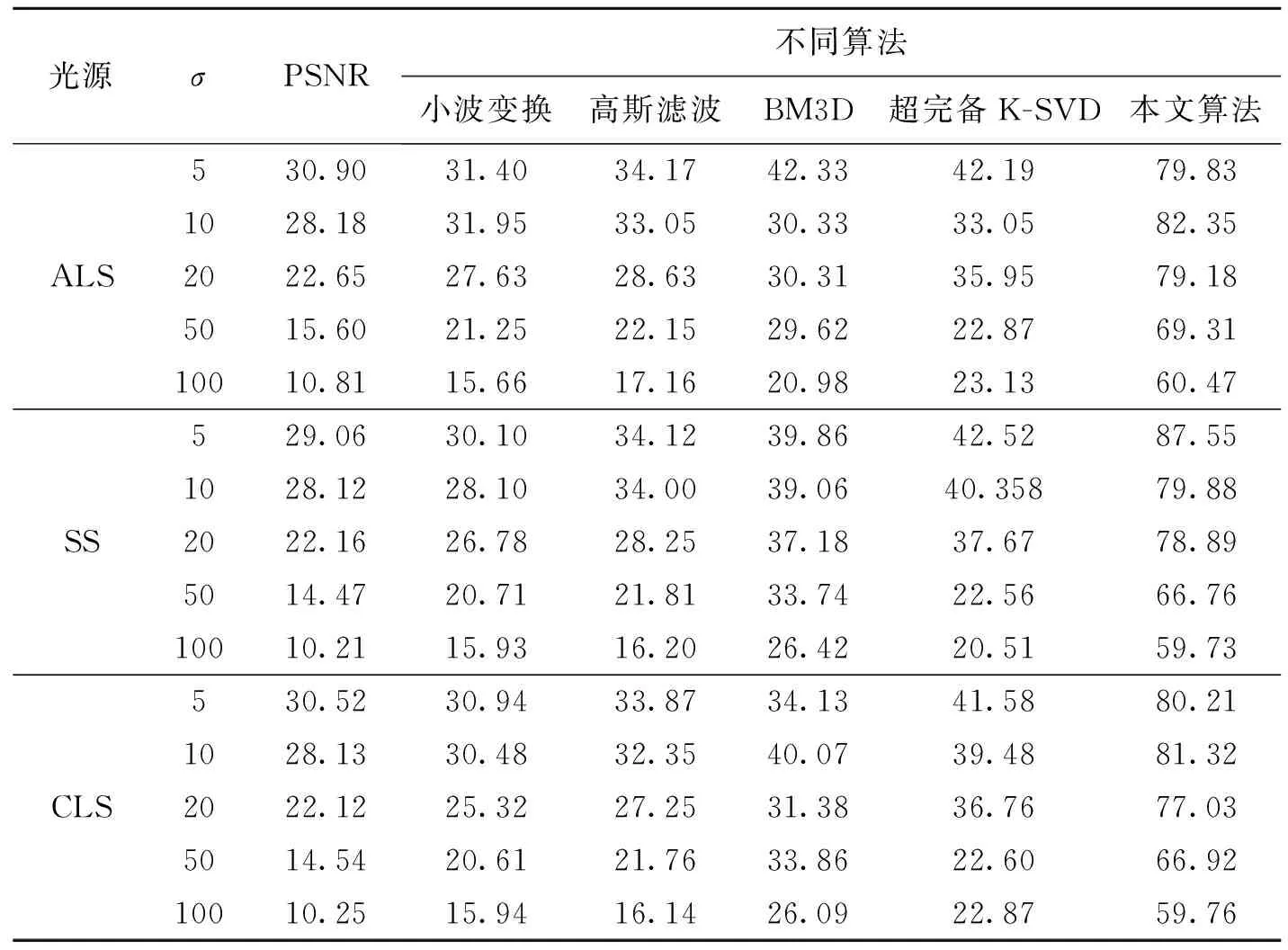
续表1 6种光源中不同噪声水平去噪的PSNR值

Table 1 The PSNR of different noise levels under 6 light sources dB

光源σPSNR不同算法小波变换高斯滤波BM3D超完备K-SVD本文算法530.9031.4034.1742.3342.1979.83 1028.1831.9533.0530.3333.0582.35 ALS2022.6527.6328.6330.3135.9579.18 5015.6021.2522.1529.6222.8769.31 10010.8115.6617.1620.9823.1360.47 529.0630.1034.1239.8642.5287.55 1028.1228.1034.0039.0640.35879.88 SS2022.1626.7828.2537.1837.6778.89 5014.4720.7121.8133.7422.5666.76 10010.2115.9316.2026.4220.5159.73 530.5230.9433.8734.1341.5880.21 1028.1330.4832.3540.0739.4881.32 CLS2022.1225.3227.2531.3836.7677.03 5014.5420.6121.7633.8622.6066.92 10010.2515.9416.1426.0922.8759.76

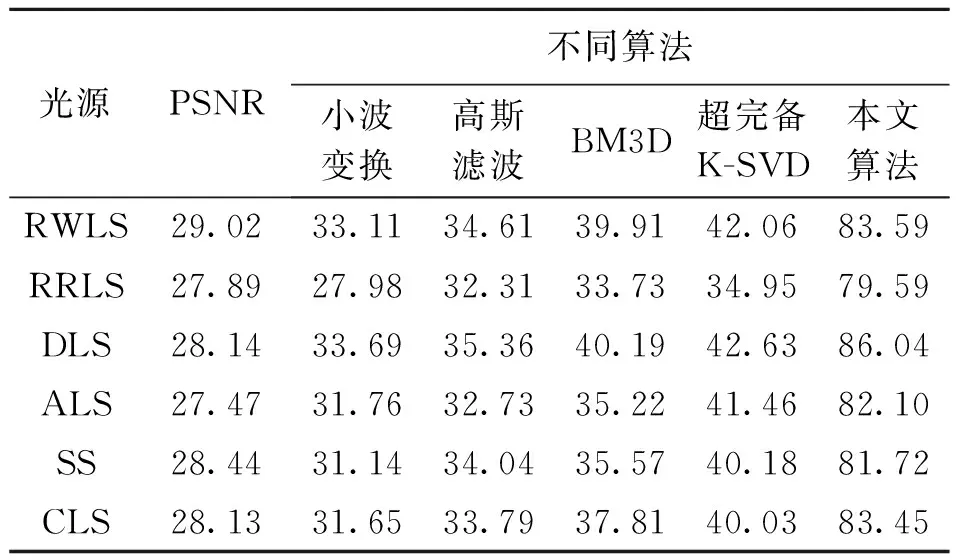
为了比较光源对去噪性能的影响,实验对规则和不规则工件在6种光源下采集到的图像进行分析．由于环境等因素的影响,使得混入工件的噪声一般在σ=5和σ=20之间,因此实验时将采集到的图像添加高斯噪声(σ=5,10,20)．实验数据如表2和表3所示(取均值)．从表2可以看出,对规则工件去噪的算法中,小波变换去噪后的PSNR值最小．高斯滤波算法去噪后的PSNR值大于小波变换,BM3D算法去噪后的PSNR值大于高斯滤波算法,超完备K-SVD算法去噪后的PSNR值大于BM3D算法．本文算法去噪后的PSNR值大于前面4种算法，且本文算法去噪后PSNR的最小值是小波变换、高斯滤波、BM3D算法、超完备K-SVD算法去噪后PSNR最大值的2.7倍，2.3倍，1.9倍，1.8倍,表明本文算法的去噪效果优于上述4种去噪算法,由于文中选用的工件结构简单,工件特征信息学习到的平方变换对特征的表征良好,达到高效去噪的目的．在同一光源下,本文算法所得到的PSNR值是小波变换、高斯滤波算法、BM3D算法、超完备K-SVD算法去噪后PSNR值的2.5倍,2.4倍,2倍．5种算法在RRLS下去噪后的PSNR值最低,在DLS去噪后的PSNR值最高,说明在DLS下采集到图像的去噪效果最优．

表2规则工件在6种光源下去噪的PSNR值

Table 2 The PSNR of regular workpiece noise under 6 light sources dB

光源PSNR不同算法小波变换高斯滤波BM3D超完备K-SVD本文算法RWLS29.0233.1134.6139.9142.0683.59 RRLS27.8927.9832.3133.7334.9579.59 DLS28.1433.6935.3640.1942.6386.04 ALS27.4731.7632.7335.2241.4682.10 SS28.4431.1434.0435.5740.1881.72 CLS28.1331.6533.7937.8140.0383.45

表3不规则工件在6种光源下去噪的PSNR值

Table 3 The PSNR of irregular workpiece noise under 6 light sources dB

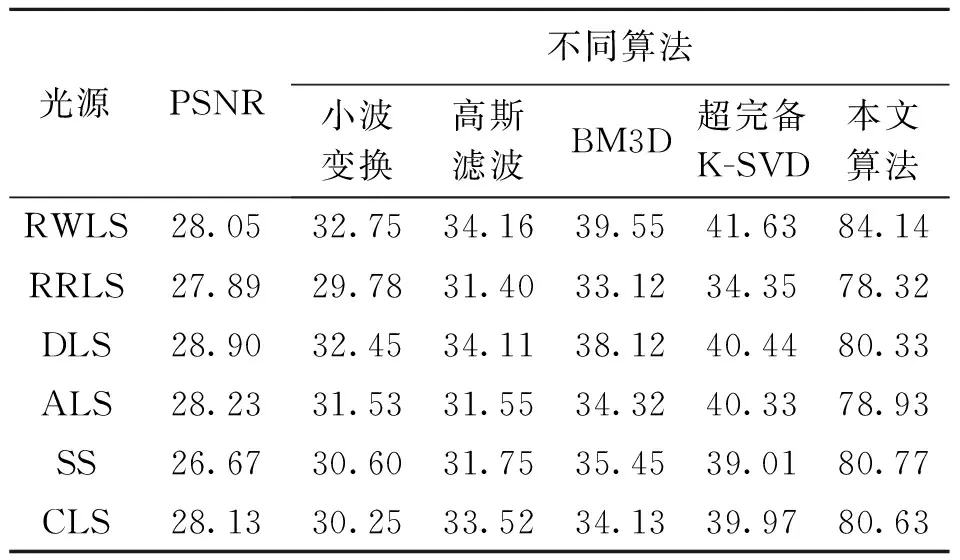
光源PSNR不同算法小波变换高斯滤波BM3D超完备K-SVD本文算法RWLS28.0532.7534.1639.5541.6384.14 RRLS27.8929.7831.4033.1234.3578.32 DLS28.9032.4534.1138.1240.4480.33 ALS28.2331.5331.5534.3240.3378.93 SS26.6730.6031.7535.4539.0180.77 CLS28.1330.2533.5234.1339.9780.63

从表3可以看出,对不规则工件去噪时,小波变换去噪后的PSNR值最小．高斯滤波算法去噪后的PSNR值高于小波变换,BM3D算法去噪后的PSNR值高于高斯滤波算法,超完备K-SVD算法去噪后的PSNR值高于BM3D算法,本文算法去噪后的PSNR值大于前面4种算法．且本文算法去噪后PSNR的最小值是小波变换、高斯滤波、BM3D算法、超完备K-SVD算法去噪后PSNR最大值的2.7倍,2.3倍,2.0倍,1.9倍,表明本文算法的去噪效果优于前面4种去噪算法．在同一光源下,本文算法是小波变换、高斯滤波算法、BM3D算法、超完备K-SVD算法去噪后PSNR值的2.9倍,2.5倍,2.1倍,2.0倍．5种算法在RRLS下去噪后的PSNR值最低,在RWLS下去噪后的PSNR值最高,说明在RWLS下对采集到图像的去噪效果最优．

3.2 视觉效果分析

为了比较不同算法去噪后的视觉效果,本文以不规则工件在RWLS下采集到的图像为代表去噪分析．图2为不规则工件图像在不同算法下去噪效果图．从图2可以看出小波变换、高斯滤波算法对噪声图像的去噪效果不明显,BM3D算法去噪后图像的边缘模糊、细节部分不清晰,K-SVD算法去噪后的图像背景中有小块,本文算法去噪后的图像背景均匀且细节明显．说明本文算法去噪后的视觉效果较好．

(a) 原图 (b) 噪声图像 (c) 小波变换 (d) 高斯滤波

(e) BM3D算法 (f) K-SVD算法 (g) 本文算法图 2 不同算法对环形白光源下不规则工件图像的去噪结果示意图Fig.2 The denoising result of irregular workpiece under DLS with different algorithms

为了更清晰展示本文算法与小波变换、高斯滤波算法、BM3D算法、K-SVD算法的细节差异,对采集到的图像进行细节放大观察,如图3所示．从图3可知,小波变换处理的图像细节模糊,而且图像背景的处理效果较差．高斯滤波处理后的图像细节较模糊,边缘和背景区分度较差．BM3D算法处理后的图像边缘模糊且阴影部分不均匀,K-SVD算法去噪后的图像细节清晰,但是背景不均匀.本文算法去噪后的效果图结合了BM3D算法和K-SVD算法的优势,背景均匀且细节清晰．从客观角度比较不同算法去噪的效果,图3(a)～(e))的数据显示本文算法去噪的PSNR值和平均结构相似度(MSSIM,mean structural sIMilarity)值．其中图3(a)的PSNR值为26.85 dB,MSSIM值为0.792 6;图3(b)的PSNR值为28.26 dB,MSSIM值为0.815 4;图3(c)的PSNR值为36.94 dB,MSSIM值为0.905 7;图3(d)的PSNR值为38.56 dB,MSSIM值为0.921 2;图3(e)的PSNR值为83.70 dB,MSSIM值为0.999 5．从数据中可以看出图3(e),本文算法的PSNR值和MSSIM值均大于上述几种算法．该算法在主观视觉角度和客观实验角度都说明本文算法的去噪性能较好．

(a) 小波变换 (b) 高斯滤波 (c) BM3D算法 (d) K-SVD算法 (e) 本文算法图 3 不同算法去噪后的细节示意图Fig.3 Detail schematic of different algorithms after denoising

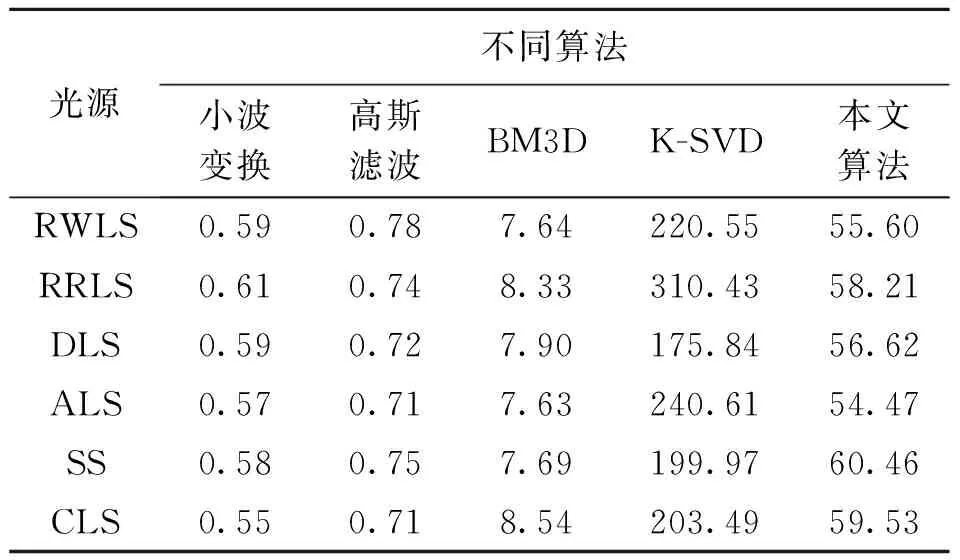
光源不同算法小波变换高斯滤波BM3DK-SVD本文算法RWLS0.590.787.64220.5555.60 RRLS0.610.748.33310.4358.21 DLS0.590.727.90175.8456.62 ALS0.570.717.63240.6154.47 SS0.580.757.69199.9760.46 CLS0.550.718.54203.4959.53

3.3 运行时间比较

对算法性能的客观评价中,时间复杂性也是一个重要的考量指标,表4是同一工件在6种不同光源下本文算法与小波变换、高斯滤波、BM3D算法、超完备K-SVD算法的去噪时间(采用均值)的比较．从表4可知,在6种光源下对工件图像进行去噪时间实验时,小波变换和高斯滤波算法去噪的时间短,BM3D算法的去噪时间较短,超完备K-SVD算法的去噪时间较长且变化幅度较大,在RRLS的去噪时间(310.43 s)略大,这是由于在环形红光源下采集到的图像背景较暗造成的．本文算法的去噪时间虽大于小波变换、高斯滤波、BM3D算法,小于超完备K-SVD算法．在保证去噪质量的前提下,本文算法的去噪时间较短,去噪速度是超完备K-SVD算法的3.9倍，在不同光源下去噪时间较稳定,说明该算法对光源具有通用性．

4 结束语

本文根据6种光源不同的特点,给出一种基于自适应平方变换的方法,并对不同光源下采集的工件图像进行去噪分析,该方法通过对图像块进行迭代学习平方变换和稀疏水平更新步骤计算去噪块来估计去噪图像．实验结果表明该方法去噪效果明显优于小波变换、高斯滤波、BM3D算法和K-SVD算法.该算法表征不规则图像全部特征时存在一定的局限性,为了更好进行工件图像分割、跟踪的工作,后续将采用联合稀疏变换学习的方法对工件图像进行去噪研究．