基于量子遗传算法优化粗糙-Petri网的电网故障诊断

田海霖,洪 良,王艺翔,王晓华

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

当前我国智能电网高速发展,电网规模和电压等级不断提高,区域电网互联程度也越来越高,对电网安全和可靠性运行也提出了更高的要求.但是,在实际运行中不可避免会发生各种故障,如雷电、覆冰、短路和接地等[1].而且电网中存在许多电容和电抗器件,会发生大量暂态过程,大容量负载的投切和不可控因素也会造成各类故障.故障发生时,调度中心收到大量报警信息,要求调度员在短时间内判断故障位置是非常困难的,但如不快速找到并消除故障,一个局部小异常都可能会造成连锁反应,导致大范围停电事故和系统崩溃.

Petri[2-4]网可以有效地描述离散事件系统,能够用图形进行直观的表示同时有严密的数学表述公式.电网故障诊断是一种离散事件过程,目前主要通过各处保护和断路器的动作情况,来判断故障的元件或位置.文献[5]是对传统Petri网的一种改进,在Petri网中引入可信度模糊知识,并加入阈值和权值,诊断结果表示其发生的概率,提高了容错性.文献[6]结合粗糙集理论和Petri网,利用粗糙集的知识提取规则,有效地提高故障识别速度.文献[7]为使Petri网更加符合电网的实际工作环境,在Petri网的变迁中加入时间限制触发条件,从而得到具有更高准确性的诊断结果.上述及文献[8-12]中的方法在电网结构简单的情况下,可以得到诊断结果,但当电网规模较复杂时,用上述系统描述,往往会发生状态空间爆炸,因此需要对数据先进行快速有效的约简.决策表中条件属性个数增长时,属性约简的难度呈指数型速度增长,是一个典型NP问题．量子遗传算法[13](QGA，quantum genetic algorithm),用量子比特[14]编码来表示染色体,用量子旋转门来完成进化,具有收敛速度快、全局搜索能力强等优点,结合粗糙集(RS，rough sets),可以快速地完成高维数据的属性约简.文献[15]直接用量子遗传算法对电网模型进行故障诊断,在主保护和断路器拒动、误动等故障情况下,都得到正确的诊断结果.但当信息缺失时,会出现漏诊或得出错误的结果等.基于此,本文结合QGA、RS和Petri网提出一种基于量子遗传算法优化粗糙-Petri网的电网故障诊断方法,可以有效解决上述方法存在的不足.大量仿真实验表明，该方法是一种速度快、准确率高、适应性强的电网故障诊断方法.

1 粗糙集理论

粗糙集理论[16]主要思想是:对数据进行划分,用已知知识库中的知识来近似表示含糊不确定的知识.

定义1 设S=(U,A,V,f)是一个信息系统.如果存在一个决策属性集合D≠∅和一个条件属性集合C≠∅,使属性集合A=(C∪D),且C∩D≠∅,则此信息系统为一个决策表,记作T=(U,A,C,D).决策表T=(U,A,C,D)是由2个信息系统SC=(U,C,V,f)和SD=(U,D,V,f)通过U,V,f之间的联系相结合的1个信息系统.它表示当某些条件满足时,应当怎样做出决策.

定义2 设T=(U,A,C,D)是一个决策表.C的所有D相对约简的族记作redD(C).如果aεC在C中是相对必需的,则称a是T的一个核心属性.T的所有核心属性形成的集合称为C的D相对核,记作coreD(C).

2 量子遗传算法

2.1 量子染色体

量子遗传算法是用量子计算优化遗传算法的智能算法.遗传算法中每段基因只能表达固定的信息,在量子遗传算法中,基因用量子比特编码,量子比特可以是|0〉和|1〉以任意概率的叠加,即可以表达更多的信息.根据叠加原理,量子比特表示如下:

|ψ〉=α|0〉+β|1〉.

(1)

式中:α和β为复数,表示量子态|ψ〉因测量导致坍缩到|0〉态和|1〉态的概率幅,且满足的归一化条件.

|α|2+|β|2=1.

(2)

用量子比特的概率幅编码染色体:

(3)

式中：θ为量子比特的相位；n为染色体个数；m为量子比特的位数，即解空间的维数；r是[0,1]范围内的随机数.

2.2 量子变异和群体灾变

在QGA中,通过量子旋转门[17]中旋转角的变化实现基因的更新和变异.定义如下:

(4)

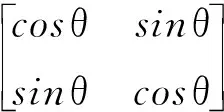
QGA算法可能会由于最优个体在连续数代的进化中都不会有任何变化而陷入局部极优值,此时需要进行群体灾变操作:最优个体保留,其余个体重新生成.使种群跳出局部优值,继续新的进化.

2.3 适应度函数

给定决策表S=(U,A,V,f),对U中种群P={p1,p2，…，pn}中的每个个体Pj(j=1,2,…,n),其适应度函数f(Pj)定义为

(5)

式中：|Pj|表示个体Pj中所含的条件属性个数;|c|表示s条件属性的个数,Yc(D)表示S中C对D的近似分类质量:

(6)

相应地,yPj(D)表示条件属性子集Pj对决策D的近分类质量.

3 Petri网理论

Petri网由库所、变迁和有相弧3个基本要素构成.定义七元组=(P,T,F,M0,M1,U,C)为一个有限的P/T系统.其中库所结点的集合为P={P1,P2,…,Pm}(m≥0),变迁结点的集合为T={t1,t2,…,tn}(n≥0)满足:P∪T≠∅,P∩T=∅,有关系F⊆(P×T)∪(T×P),dom(F)∪cod(F)=P∪T.M0为初始状态标识,M1为变迁点火后的状态标识,关联矩阵C表示库所与变迁之间的输入输出关系,转移控制矢量U表示系统变迁点火序列.

Petri网中,变迁的触发引起token的流动,进而形成动态的系统.变迁触发规则如下:

(1) 若变迁t的每个输入库所P都存在token,那么t在标识M有触发权;

(2) 若变迁t在标识M有触发权,则t触发,token从输入库所流向输出库所,从而产生新的标识,在初始标识M0下,有触发权的变迁触发就能得到新标识1.如图1所示是逻辑规则的Petri网.

4 基于RS-QGA和FPN算法实现

本文针对电网故障,通过结合 RS-QGA和FPN的方法进行故障诊断．算法具体实现步骤如下.

图 1 电网结构实例Fig.1 Grid structure instance

输入:初始决策表S,种群规模n,量子比特数目m,进化代数t,最大迭代次数δ,灾变阈值代数I;

输出:故障区域.

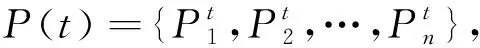
(7)

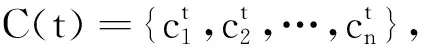
Step 3:采用适应度函数f(Pj)评价种群中所有个体,使f(Pj)max个体进入下一代.如果f(Pj)max个体连续I代没有任何变化,则对群体进行灾变操作,即只保留f(Pj)max个体,其余个体基因随机初始化重新生成种群;

Step 4:使用量子旋转门策略更新各染色体;

Step 5:进化代数增加1,若t满足δ,则输出约简后的决策表S′,否则执行Step 3;

Step 6:建立符合电网结构的Petri网模型.根据约简后的决策表S′,提取出条件属性B所对应的报警信息,以条件属性的取值作为Petri网初始库所,库所中托肯的分布,即为Petri网模型初始标识向量N0;

Step 7:根据触发点火规则,对满足触发条件的变迁节点依次点火,待点火全部完成后,Petri网进入稳定状态,得到终态标识向量M1;

法国的法律繁复，有许多艰涩的法律条文，为了准确翻译它们，我查遍翻烂了几本法中字典、法规词汇等，甚至还经常需要通宵达旦地奋战，才能找到适合的字句。

Step 8:根据终态标识向量M1保护设备动作进行评价,得出故障区域.

5 仿真算例

采用如图1所示供电网结构实例进行故障诊断分析.该电网分为sec1～sec7 7个供电区域,每个区域线路上都分别带有断路器(CB1～CB7)和过流保护(CO1～CO7).sec1线路上所带距离保护RR1为sec2～sec7的后备保护.sec2线路上所带距离保护RR2为sec3～sec5的后备保护.

根据上述电网结构实例,结合粗糙集理论可知:条件属性C和决策属性D分别对应断路器、各保护的状态和故障区域.其中,条件属性包括7个断路器(CB1～CB7),7个过流保护(CO1～CO7)和2个后备保护(RR1和RR2),共16个.决策属性包括7个故障区域(sec1～sec7).条件属性有“0”和“1”2种状态,“0”表示断路器闭合或保护未动作,“1”表示断路器断开或保护动作.基于以上实例,通过电路结构分析并结合继电保护动作原理,得到电网故障诊断初始决策表,如表1所示.

输入表1所示种群规模为12,量子比特为16的初始决策表,最大迭代次数设为500,灾变阈值设为50.通过对种群中个体观测生成观测结果,然后采用适应度函数f(Pj)进行评价,保留最优个体进入下一代,满足灾变条件则进行灾变操作,使用量子旋转门策略更新染色体,依次迭代达到最大迭代次数输出约简后决策表如表2所示.

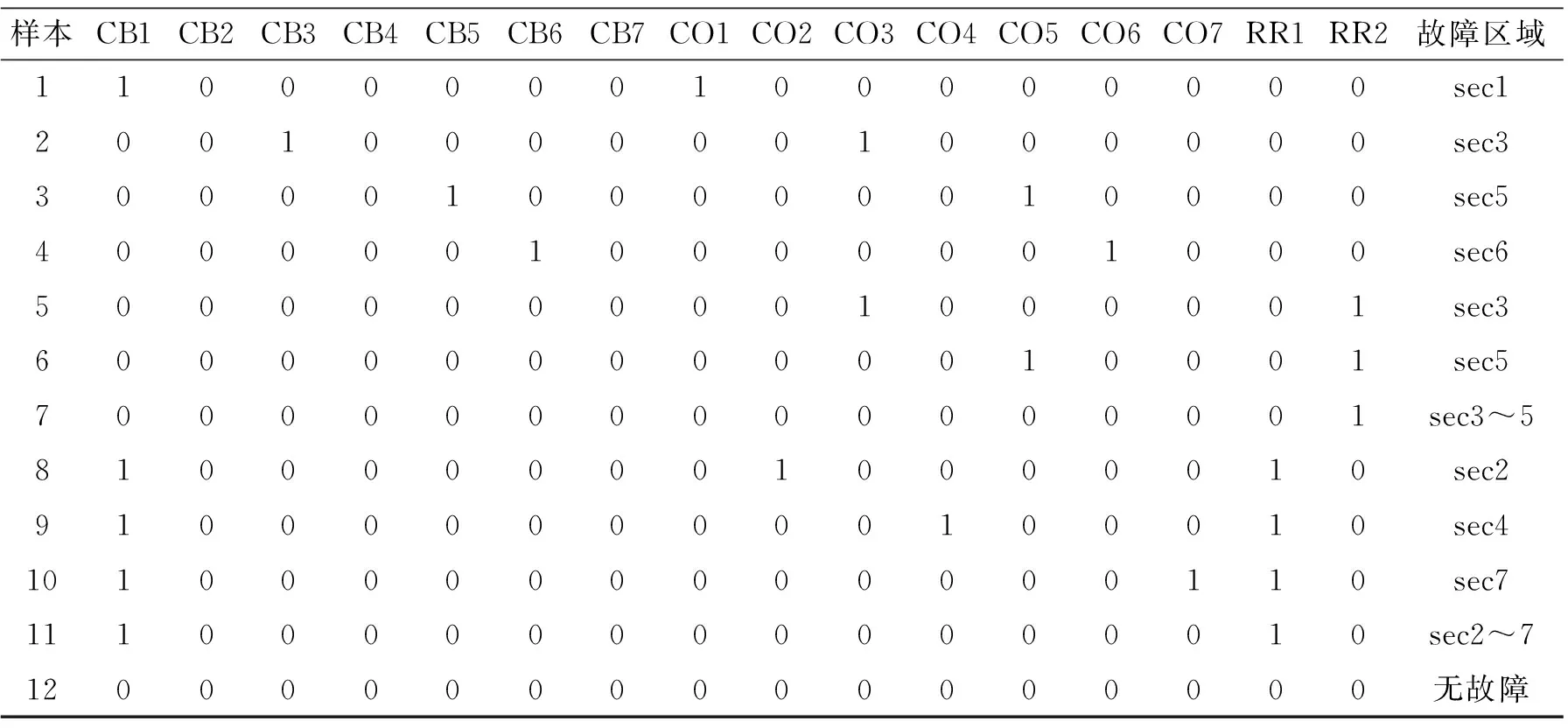
表 1 电网故障诊断初始决策表Table 1 Original decision Table of power grid fault diagnosis

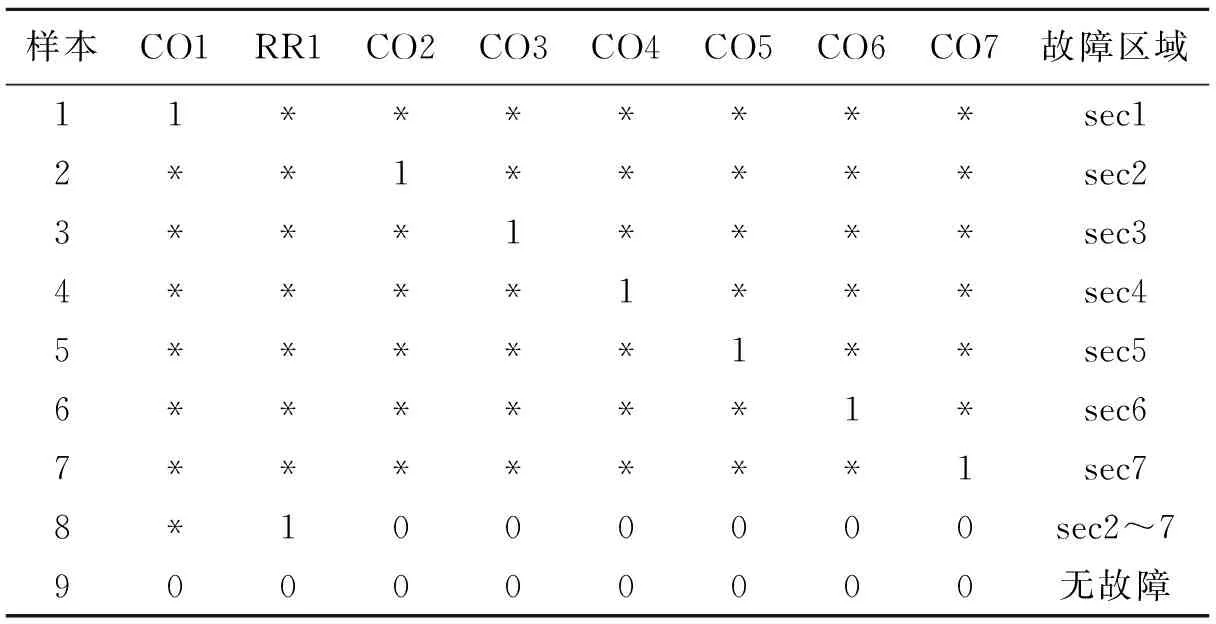
表 2 约简后最小决策表Table 2 Minimal decision Table after reduction

注:*表示可以在0，1中取值

通过表2可以看出,约简后最小决策表大大减小了初始决策表的属性维度,降低了电网故障诊断复杂度.但是却具有和初始决策表相同的决策能力.由表2可以得到以下9条产生式规则:

(1) 若CO1=1,则故障在sec1;

(2) 若CO2=1,则故障在sec2

(3) 若CO3=1,则故障在sec3;

(4) 若CO4=1,则故障在sec4;

(5) 若CO5=1,则故障在sec5;

(6) 若CO6=1,则故障在sec6;

(7) 若CO7=1,则故障在sec7;

(8) 若RR1=1，CO2=0，CO3=0，CO4=0，CO5=0，CO6=0，CO7=0,则故障在sec2～sec7;

(9) 若所有条件属性都为0,则无故障.

基于上述9条产生式规则和Petri网逻辑规则,建立如图2所示Petri网故障诊断模型.通过Matlab仿真,对表3中10处预设故障进行诊断,均诊断出正确的故障区域.而且从表中可以看出,在断路器拒动或误动以及某些断路器动作信息不确定的情况下,同样诊断出正确的故障区域,说明该故障诊断模型具有良好的鲁棒性和容错性.

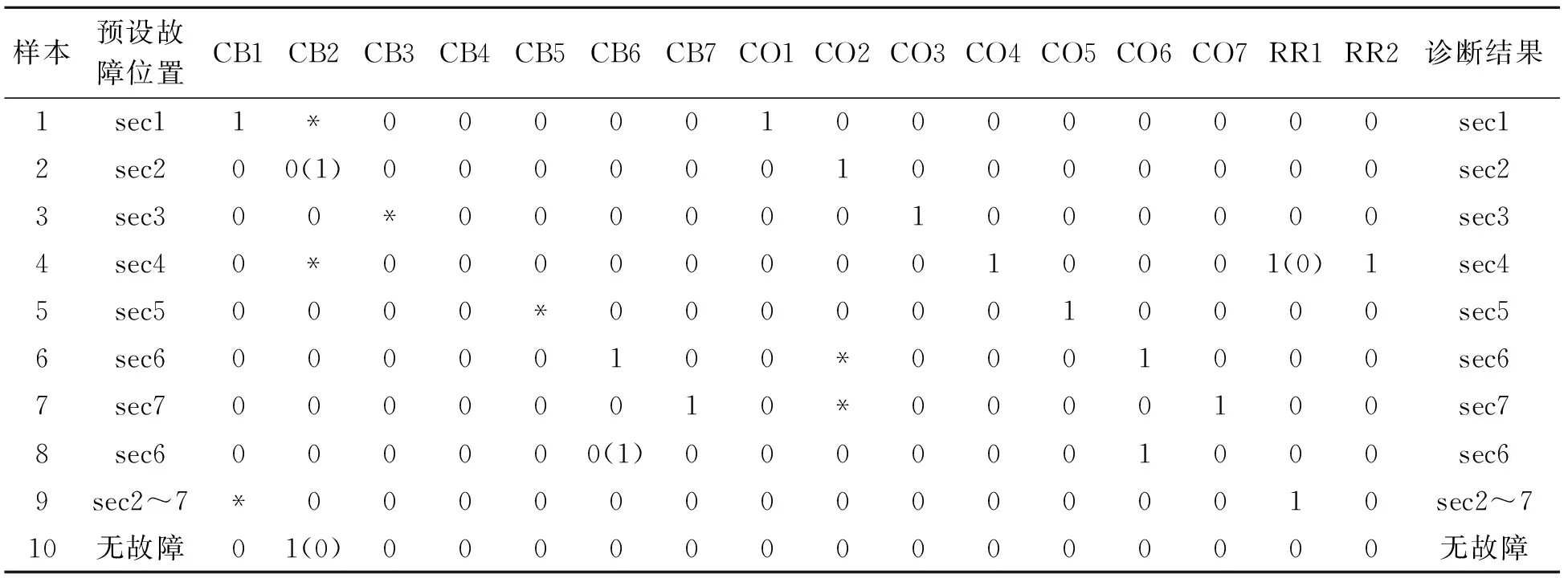
表 3 电网故障诊断仿真结果Table 3 Fault diagnosis results

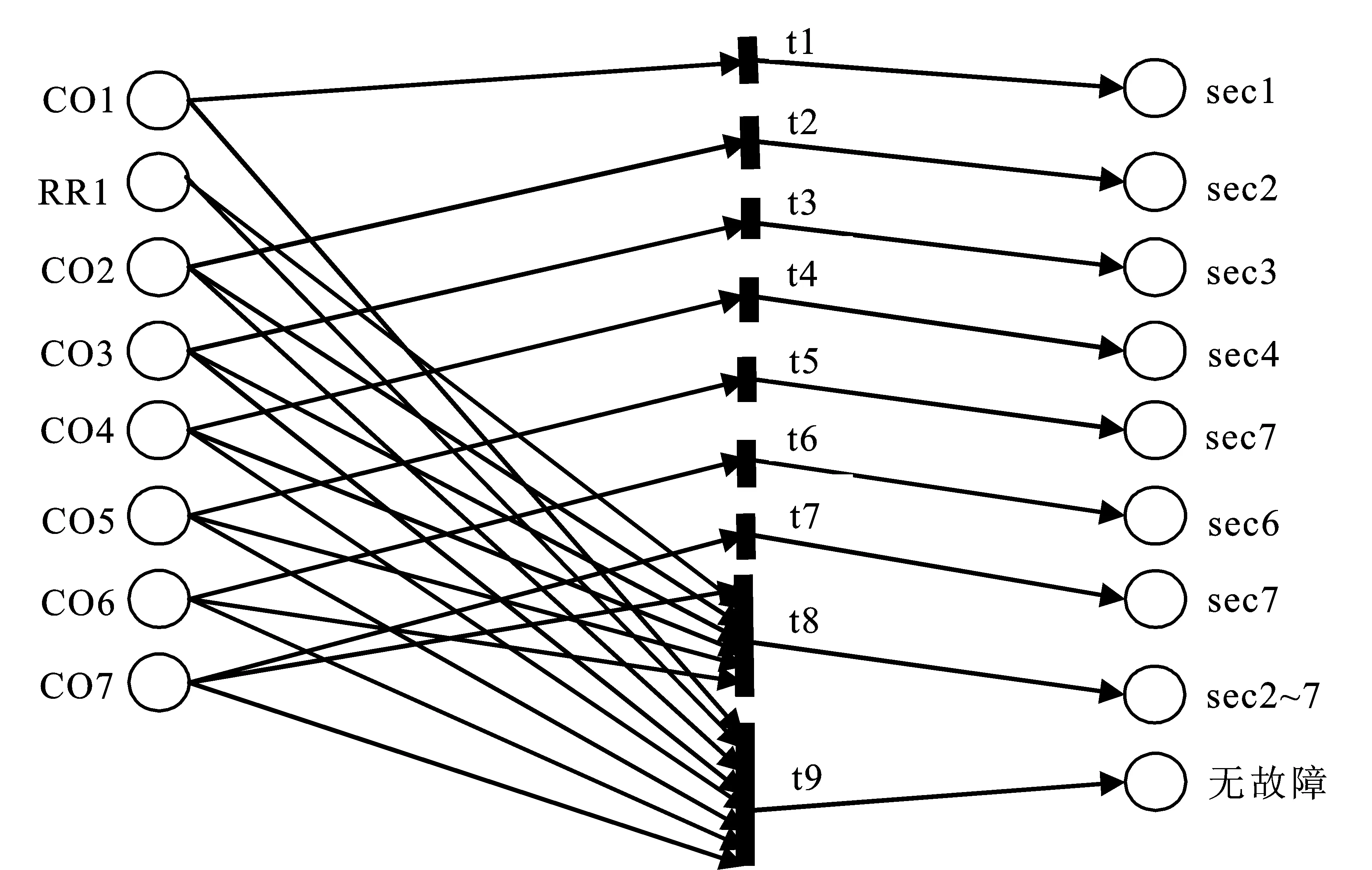
图 2 故障诊断Petri网模型Fig.2 Petri nets model of fault diagnosis

6 结束语

本文通过分析上述智能算法的优缺点,提出了一种基于量子遗传算法优化粗糙-Petri网的电网故障诊断方法.在当前实际电网高度智能化的背景下,对故障诊断的快速准确性的要求不断提高.量子遗传算法有效地对故障数据进行属性约简,降低故障属性维度,结合Petri网对电网故障离散事件的高效处理能力,提高了故障诊断效率.实例仿真结果表明,该方法具有较高的准确率和较快的处理速度.对实现复杂电网的高效准确诊断具有重要的实际意义.