克里雅绿洲浅层地下水与土壤特征的局部空间关系

黄 玲, 瓦哈甫·哈力克, 卢龙辉

(1.新疆大学资源与环境科学学院; 2.新疆大学绿洲生态教育部重点实验室;3.新疆大学旅游学院，新疆 乌鲁木齐 830046)

水是干旱区最关键的生态环境因子[1]，并且，干旱区直接影响植被生长的土壤水分和盐分与地下水密切相关[2]。水土关系的不平衡可能导致盐渍化等类型的土地退化。盐渍化作为影响生态环境的重要因素[3]，将直接决定生态系统的生产力、水分与能量的平衡交替[4]。深入研究干旱区水土空间关系，对维持绿洲系统的稳定性与安全具有重要意义。

在水土研究的初期，水土相互影响的研究主要以定性的总体分析为主(1994-2002年)[5-6]。随着定量方法的发展，以及空间数据处理技术的进步，插值方法与经典统计方法被引入水土关系的研究(2007-2012年)[7-10]。近年来，对水土关系的研究开始综合不同的分析方法，如经典统计分析、插值法、地统计方法(Moran’I)、耦合模型等(2014-2016年)[11-14]。在水土关系研究方法不断改进的过程中，空间插值法被广泛应用，IDW(Inverse Distance Weighted，反距离权重法)[15]、RBF(Radial Basis Function，径向基函数法)[16]、普通克里格法(Ordinary Kriging)[17]方法已被众多地理学者认可。统计分析方面，主要运用全局尺度相关分析，如经典统计方法(回归等)、Pearson’s相关分析及地统计方法。但目前对于局部尺度相关分析的研究还不多见。遥感技术、空间统计方法、地理信息技术的发展为水土关系分析提供了有力工具，尤其是GWR(Geographically Weighted Regression，地理加权回归)在探索变量间相互关系的异质性和空间自相关方面有明显优势[18-20]。如果能够同时运用全局尺度与局部尺度统计分析，且综合地理信息技术在空间上区分相关性的异质特征，将对浅层地下水特征与表层土壤特征间相互关系的研究有很大助益。

克里雅绿洲作为典型的干旱区绿洲区域，进行干旱化与盐渍化的研究非常迫切，尤其在探讨区域水土特征关系方面。本研究通过遴选最优插值方法，借助网格单元法，尝试在结合传统统计方法与空间统计方法的基础上，重点研究全局尺度统计与局部尺度统计在水土空间数据分析上的应用，为进一步研究浅层地下水特征与表层土壤特征的相互影响奠定基础。

1 研究区概况

克里雅绿洲位于中国新疆南部，隶属于和田地区于田县，地理位置为81°09′～82°51′E、35°14′～39°29′ N，地处克里雅河流域山前平原区域，位于塔克拉玛干沙漠与喀拉昆仑山之间。克里雅河自南向北贯穿绿洲，多年平均径流量为6.99×108m3[15]，占绿洲水资源利用总量的82.1%。克里雅绿洲属于暖温带大陆干旱荒漠气候，多年平均降水量为47.7 mm[16]，多年平均蒸发量为2 432.1 mm，降水稀少而蒸发量大。

2 数据与研究方法

通过在绿洲区域内均匀分布的24个观测井(见图1)内安装水位深度记录仪/监测仪(HOBO U20-001-02)与电导率测量记录仪(HOBO U24-002-C)进行地下水数据采集，间隔为1次/h。通过在观测井附近1m范围内安装土壤水分传感器(ECH2O 5TE)与五通道土壤数据采集器(EM50)进行表层(0～20、20～40、40～60、60～80、80～100 cm共五层)土壤数据采集，间隔为1次·h-1。

本研究获取到2015年全年地下水与表层土壤实测数据。考虑到表层土壤0～20 cm处为土壤盐分的主要影响层[19]，本研究主要分析表层(0～20 cm)土壤特征数据。排除突变数据及无效数据后，计算地下水埋深、地下水电导率、表层土壤含水率、表层土壤电导率4个指标的年平均值。通过SPSS 19.0进行对数转换，运用ArcGIS 10.0中三种较为常用的空间插值方法(普通克里格法、IDW、RBF)分析最优的地下水与表层土壤特征插值方法，并进行交叉验证及精度检验(ME平均误差、RMSE均方根误差)。本研究运用网格单元法(Grid Cell Method)对空间插值预测结果进行网格化处理(1 km×1 km)，通过Pearson’s相关系数分析4个指标间在总体上的统计相关。通过GWR(地理加权回归)与OLS(最小二乘法)模型精度对比分析最优的局部空间相关模型，研究地下水与表层土壤4个指标间在局部上的空间统计相关。

图1 研究区位置、井位分布图Fig.1 Location of the study area and distributionof sampling wells

3 结果与分析

3.1 最优空间插值方法与预测结果分析

对地下水埋深、地下水电导率、土壤含水率、土壤电导率数据均进行3次不同方法(普通克里格法、IDW、RBF)的空间插值(对比结果见表1)。RBF插值法拟合地下水埋深、表层土壤电导率精度最高，IDW法拟合地下水电导率的精度优于其它两种方法，表层土壤含水率更适于采用普通克里格法。三种插值方法采用对数转换后数据的精度普遍优于采用原始数据的精度(ME与RMSE更小[17])，但普通克里格法采用原始数据的精度更高，因此本研究将采用对数转换后数据进行地下水埋深、地下水电导率、表层土壤电导率的空间分布预测，采用原始数据进行表层土壤含水量的空间分布预测。为获得最优(精度最高)空间分布预测，本研究运用RBF法对地下水埋深、表层土壤电导率进行空间插值，IDW法对地下水电导率进行插值，普通克里格法对表层土壤含水率进行空间插值预测。

分析地下水埋深、地下水电导率、土壤含水率、土壤电导率的空间分布预测结果(见图2)，结果显示：不同指标表现出不同的空间分布特征。在绿洲区域内，地下水埋深跨度较大，变化范围为0.65 ～13.69 m，平均埋深约2.33 m，由于海拔的影响，总体呈现由西北至东南逐渐增加的趋势。由于河道与绿洲湿地的交替分布引起的地下水补给差异，地下水水位最高值位于绿洲西部湿地(龙湖湿地)区域以及东部稻田区域。地下水电导率总体由西南至东北依次呈现低-高-低的变化特征，平均电导率约为3.1 mS·cm-1。表层土壤电导率与表层土壤含水率呈现较为一致的分布特征，由绿洲西部至东部依次呈现低-高-低-次高的特征。表层土壤电导率与表层土壤含水率的两个最高值基本出现在相同的区域，很可能与湿地的盐分聚积效应有关。另外值得注意的是，受河流-地下水的动态相互补给过程的影响，沿河道一定范围内的土壤含水率均较高而土壤电导率均较低。

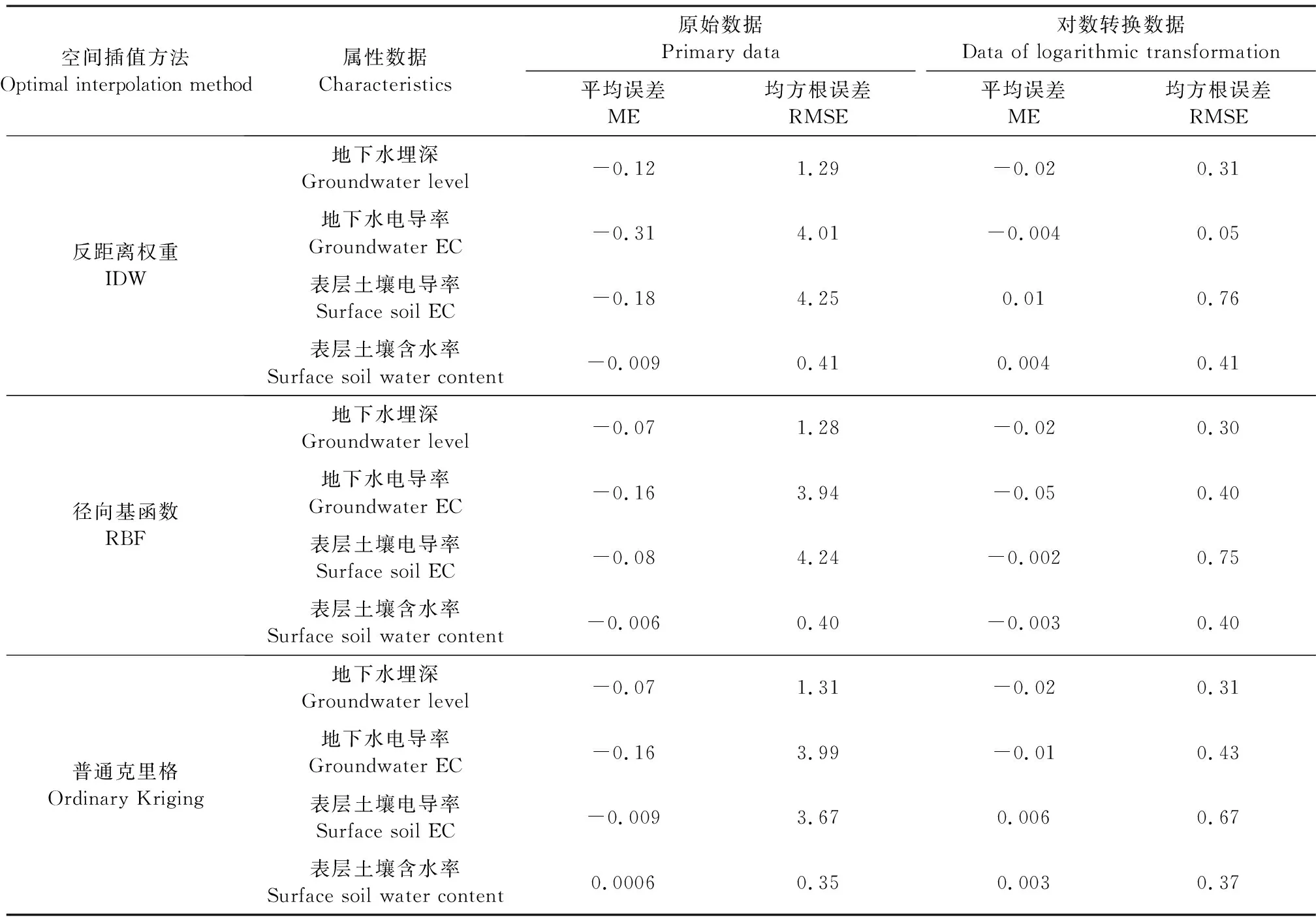
表1 浅层地下水与表层土壤特征的最优空间插值方法

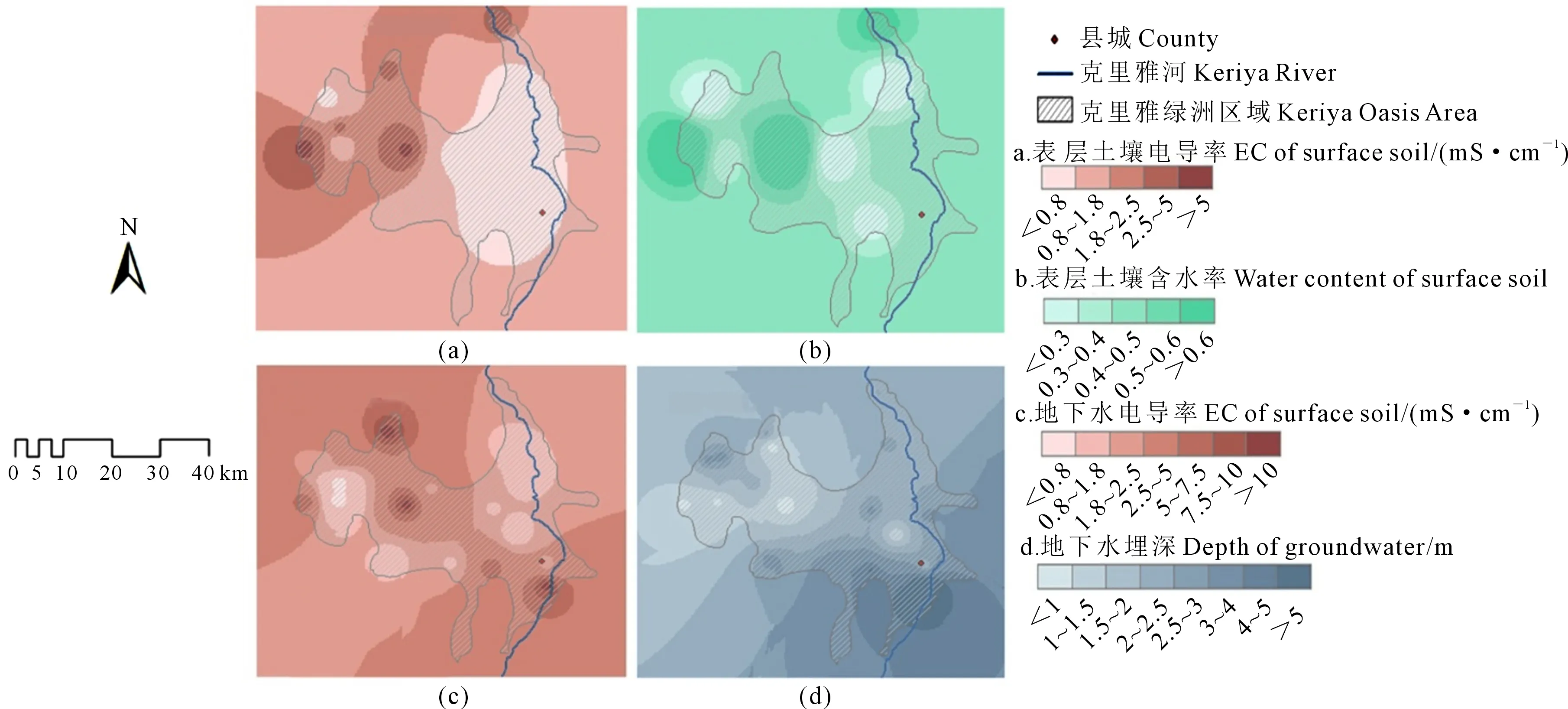
图2 浅层地下水与表层土壤特征的空间分布预测Fig.2 Predicted spatial distribution for characteristics of shallow groundwater and surface soil

本研究运用ArcGIS 10.0的数据管理-要素类创建渔网工具，对土壤电导率、土壤含水率、地下水埋深、地下水电导率4个指标的插值结果(栅格数据)进行分级，将转换的矢量面状文件进行网格单元化，网格大小1 km×1 km，结果见图3(以表层土壤电导率网格单元化为例)。

Pearson相关系数矩阵显示了土壤电导率、土壤含水率、地下水埋深、地下水电导率网格单元数据之间的总体相关性大小(见表2)。土壤电导率与土壤含水率的线性相关程度达到0.850，表明土壤含水率对土壤盐分的影响非常高，这与已有的研究结论相反[18]，可能由于克里雅绿洲典型的灌溉农业与干旱区蒸发量较大综合作用导致土壤含水率越高洗盐量也越高。土壤电导率与地下水埋深的线性相关系数为-0.459，与地下水电导率的相关系数为0.602，表明土壤电导率受地下水的影响较为明显，地下水电导率与土壤电导率的相关程度更高。地下水电导率与埋深的相关系数为-0.474，基本与土壤电导率、埋深两者的相关系数(-0.459)持平，表明地下水埋深对地下水电导率与土壤电导率的影响基本相同。所有相关系数均通过了显著性检验，为极显著水平。

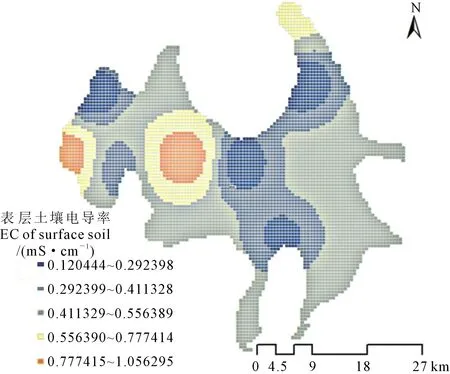
图3 网格单元化Fig.3 Results of grid cell method for predicted ECvalue of surface soil

Pearson’s系数Pearson’s correlation地下水埋深Groundwater level 地下水电导率Groundwater EC 表层土壤含水率Surface soil water content 表层土壤电导率Surface soil EC地下水埋深Groundwater level1地下水电导率Groundwater EC-0.474**1表层土壤含水率Surface soil water content-0.475**0.311**1表层土壤电导率Surface soil EC-0.459**0.602**0.850**1

注：**表示在0.01水平(双侧)上显著相关。

Note: ** denotes the significance level ofP≤ 0.01.

3.3 GWR与OLS模型对比与局部尺度空间回归分析

3.3.1 GWR与OLS模型对比及相关分析 对比GWR与OLS两种空间回归建模方法(见表3)，由于表层土壤电导率与表层土壤含水率存在很强的多重共线性，即存在较明显的相同变化趋势，采用OLS模型即可。其余指标间构建的模型对比结果显示：采用GWR模型的校正R2均有较大提高，模型的解释程度平均提升幅度为552%(R2越高变量解释的程度越高[19])；除地下水埋深与地下水电导率所构建模型外，均为GWR模型的AICC值更低(AICC越低表明模型预测结果与实际结果越接近[20])。为更精确地研究局部空间相关，本研究对表层土壤电导率与表层土壤含水率构建OLS模型，对土壤电导率与地下水电导率、土壤电导率与地下水埋深、地下水电导率与地下水埋深构建GWR模型。在空间上，对于表层土壤电导率，表层土壤含水率可以解释63.1%的变化，地下水电导率可以解释78.9%的变化，地下水埋深可以解释49.5%的变化；对于地下水电导率，地下水埋深可以解释61.4%的变化。

3.3.2 局部尺度空间回归结果在空间的异质性 OLS模型结果的估计、残差参数与GWR模型结果的局部回归系数、LocalR2见图4～图7。相比土壤电导率与土壤含水率的Pearson’s相关系数为极显著的0.85(见表2)，OLS模型结果(图4)显示绿洲内部在空间上存在高低不同的相关性，绿洲西部相关性明显高于东部。残差显示OLS模型在大部分区域拟合效果较好(残差绝对值小)。

土壤电导率与地下水电导率的GWR模型(图5)结果，与Pearson’s相关分析结果(极显著正相关0.602，见表2)不同，同时出现了正相关与负相关特征。负相关存在于绿洲中部灌溉频繁的耕地区域很可能的原因是灌溉对土壤的脱盐作用，尤其在稻田区域出现了最大的负相关(图5左，中部深蓝色环形区域)。

同样的空间异质特征也出现在土壤含水率与地下水埋深的局部回归结果中(图6)。总体Pearson’s相关系数为显著的负相关-0.459(见表2)，但局部空间回归的结果表明在绿洲东部区域存在正相关。不过结合绿洲西部呈现负相关的区域模型拟合效果较好，这种正相关的解释程度并不高。在湿地区域，由于地下水位较低，土壤电导率与埋深的相关也较好，呈现显著负相关。

地下水电导率与地下水埋深的GWR模型拟合结果同样呈现出空间相关的异质性(图7)。在总体呈负相关(见表2)的情况下，局部地区呈现出正相关的特征。

以上研究表明，将GWR方法运用在空间数据的统计分析方面能够反映更多的异质特征，而OLS模型只在近似线性的数据的处理分析上效果更好。

4 讨 论

在众多空间插值方法的选择上，不同的区域应当选取适用于研究区的插值方法，通过交叉验证与精度检验可以对插值方法进行优选。虽然本研究所选取的插值方法只适用于克里雅绿洲，但是选取插值方法依据的原则可以为其它区域的研究提供借鉴。

表3 GWR与OLS模型精度对比结果

Table 3 Comparison of GWR and OLS models accuracy

属性数据Characteristics模型Model表层土壤含水率Surface soil water content 校正R2Adjust R2AICC地下水电导率Groundwater EC 校正R2Adjust R2AICC地下水埋深Groundwater level校正R2Adjust R2AICC属性数据Characteristics地下水埋深Groundwater depth校正R2Adjust R2AICC表层土壤电导率Surface soil EC GWR0.789-12189.70.495-7723.5OLS0.631-93460.101-4781.10.094-4737地下水电导率Groundwater EC 0.61415224.50.094-4737

注：空白表示未能成功建立模型(存在严重多重共线性)，模型在0.05水平上均具有显著性。

Note: Blank spaces mean there were no successful models due to severe multiple linearity; all models showed here are significantly atP≤0.05 level.

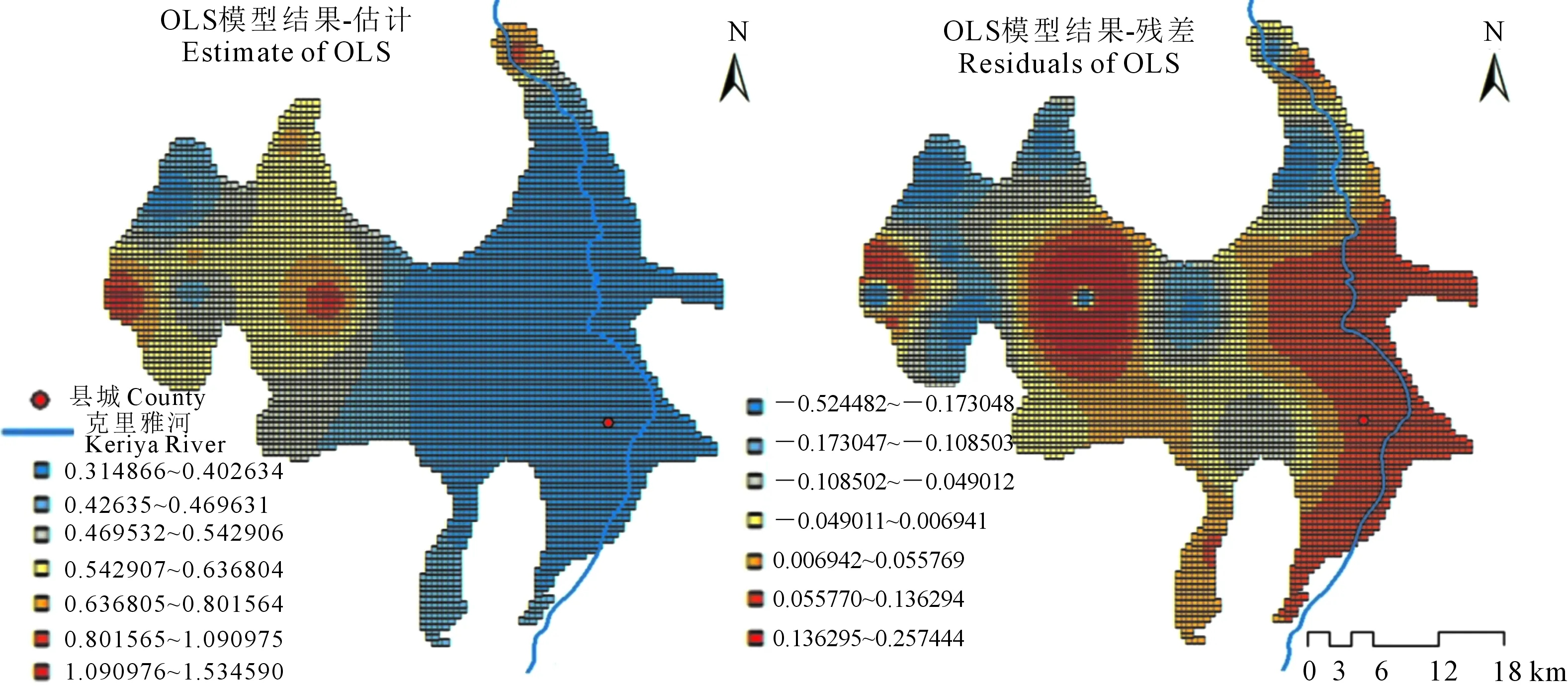
图4 土壤电导率与土壤含水率局部相关的空间变异(OLS模型)Fig.4 Spatial variation of regression outputs from OLS model of soil EC and soil moisture content

图5 土壤电导率与地下水电导率局部相关的空间变异(GWR模型)Fig.5 Spatial variation of regression outputs from GWR model of soil EC and groundwater EC

图6 土壤电导率与地下水埋深局部相关的空间变异(GWR模型)Fig.6 Spatial variation of regression outputs from GWR model of soil EC and groundwater level

图7 地下水电导率与地下水埋深局部相关的空间变异(GWR模型)Fig.7 Spatial variation of regression outputs from GWR model of groundwater EC and groundwater level

另外，本研究表明地统计空间插值方法适用于地下水特征与土壤特征的研究，但值得探讨的是，在其它研究领域的数据是否同样适用。

网格单元法在处理大尺度的地理空间数据上具有明显的优势。本研究借鉴常运用于大尺度空间数据处理的网格单元法，并且尝试将其运用于县域尺度的空间数据上，研究结果显示网格单元法既便于进行数据空间分析，也能够保证数据质量，且效果较好。但是，本文未对MAUP(可变面积单元)问题进行探讨，网格单元大小的不同对研究结果会造成多大的影响，将是下一步研究的问题。另外，网格单元法在点面数据转换方面具有一定优势，未来可以扩展应用至其它研究领域，尤其在社会、经济数据处理方面，能够为社会学科与自然学科的交叉研究提供有效的帮助。

统计方法已经普遍运用于各个研究领域的数据分析方面，而地统计技术及地理空间分析技术为相关科学研究提供了更多的分析维度。本研究结合了传统统计方法与空间统计方法，运用全局尺度统计与局部尺度统计对地下水与表层土壤空间数据进行了分析。在关注全局尺度统计结果的同时，更关注局部尺度统计的结果。另外需要注意空间统计模型的精度问题，探讨空间统计模型在不同研究领域、不同数据源的适用性，这将为不同学科的研究提供依据。

5 结 论

1)地下水埋深总体呈现由西北至东南逐渐增加的趋势，地下水电导率总体由西南至东北依次呈现低-高-低的变化特征。表层土壤电导率与表层土壤含水率呈现较为一致的分布特征，由绿洲西部至东部依次呈现低-高低-次高的特征。RBF插值法拟合地下水埋深、表层土壤电导率精度最高，IDW法拟合地下水电导率的精度优于其它两种方法，表层土壤含水率更适于采用普通克里格法。

2)空间关系模拟方法上，表层土壤电导率与表层土壤含水率存在很强的多重共线性，采用OLS模型，其余指标间构建的模型对比结果显示GWR模型更优。

3)空间相关性上，土壤含水率对土壤盐分的影响较高，土壤电导率受地下水的影响较为明显，地下水埋深对地下水电导率与土壤电导率的影响基本相同。土壤电导率与土壤含水率的全局相关性为极显著正相关(0.85)，局部相关性上绿洲西部明显高于东部；土壤电导率与地下水电导率的全局相关性为极显著正相关(0.602)，但局部相关性上同时具有正相关与负相关特征，负相关主要出现在绿洲中部灌溉频繁的耕地区域；土壤含水率与地下水埋深的全局相关性为显著负相关(-0.459)，但绿洲东部存在局部的正相关；地下水电导率与地下水埋深全局呈负相关，局部出现正相关。

4)GWR方法较OLS方法反映更多的异质特征，在总体相关水平下局部区域可能出现方向相反或大小不等的相关性。本研究表明在全局尺度统计分析显示的特征之外，局部尺度统计分析更能反映复杂的特征，更接近实际情况，提供的分析维度与深度更优、信息更丰富。本研究能为当地的水土资源管理实践提供实际的参考依据，帮助当地有关部门加深对水土相互影响的认识。本文在丰富水土关系研究方法的同时，建议未来的相关研究能够综合遥感、GIS、多种统计方法，希望能为进一步的干旱区地下水与土壤相互关系研究提供科学的依据。