ON THE NORMALIZED LAPLACIAN SPECTRUM OF A NEW JOIN OF TWO GRAPHS∗

Xianzhang Wu,Lili Shen

(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)

Abstract Given graphs G1and G2,we define a graph operation on G1and G2,namely the SSG-vertex join of G1and G2,denoted by G1⋆G2.Let S(G)be the subdivision graph of G.The SSG-vertex join G1⋆G2is the graph obtained from S(G1)and S(G2)by joining each vertex of G1with each vertex of G2.In this paper,when Gi(i=1,2)is a regular graph,we determine the normalized Laplacian spectrum of G1⋆G2.As applications,we construct many pairs of normalized Laplacian cospectral graphs,the normalized Laplacian energy,and the degree Kirchho ffindex of G1⋆G2.

Keywords spectrum;SSG-vertex join;normalized Laplacian cospectral graphs;normalized Laplacian energy;degree Kirchho ffindex

1 Introduction

All graphs described in this paper are simple and undirected.Let G be a connected graph with vertex set V(G)={v1,v2,···,vn}and edge set E(G)={e1,e2,···,em}.The adjacency matrix of G is A(G)=(aij)n×nwith aij=1 if viis adjacent to vj,and aij=0 otherwise.Let D(G)=diag(d1,d2,···,dn)be the diagonal matrix of vertex degrees of G.The Laplacian matrix and the normalized Laplacian matrix are defined as L(G)=D(G)−A(G)and L(G)=,respectively.The characteristic polynomial of L(G)is defined as fG(L(G):x)=det(xEn−L(G)),where Enis the identity matrix of order n.The roots of fG(L(G):x)=0 is called the normalized Laplacian eigenvalues of G,denoted by γ1(G),γ2(G),···,γn(G),where γn(G)=0.Since A(G)is a real symmetric matrix,its eigenvalues are all real numbers.Their eigenvalues are conventionally denoted and arranged as λ1(G) ≥ λ2(G) ≥ ···≥ λn(G).The set of all the eigenvalues together with their multiplicities is called the A-spectrum of G.Graphs G1and G2are called normalized Laplacian cospectral if they have the same normalized Laplacian spectrum.The incidence matrix R of G is a(0,1)matrix with rows indexed by vertices and column indexed by edges,where Rve=1 when the vertex v is an end point of the edge e and 0 otherwise.The subdivision graph of G,denoted by S(G),is the graph obtained by inserting a new vertex into every edge of G.Undefined terminology and notations may refer to[1].

Spectral graph theory is a fast growing branch of algebraic graph theory and concerns an interwind tale of properties of graphs and spectrum of related matrices.Calculating the spectra of graphs as well as formulating the characteristic polynomials of graphs is a fundamental and very meaningful work in spectra graph theory.The characteristic polynomial and spectra of graphs help to investigate some properties of graphs such as energy[2,3],the Kircho ffindex[4-6],the Laplacian-energy-like invarients[7,8],the normalized energy[15,16],the degree Kircho ffindex[17],and so on.Recently,many graph operations such as the subdivision join,the corona,the edge corona and the neighbour corona have been introduced,and their spectrum are computed[9-13].

Motivated by the above works,given graphs G1and G2,we define a new join of graphs G1⋆G2and obtain their normalized Laplacian spectrum when G1and G2are regular graphs.As applications,we construct many pairs of normalized Laplacian cospectral graphs,the normalized Laplacian energy,and the degree Kirchho ffindex of G1⋆G2.

2 Normalized Laplacian Spectrum of A New Join of Two Graphs

In this section,we first define a new join of graphs G1⋆G2and list some known results,then determine the normalized Laplacian spectrum of G1⋆G2when G1,G2are regular graphs.Moreover,we also construct many pairs of normalized Laplacian cospectral graphs,the normalized Laplacian energy,and the degree Kirchho ffindex of G1⋆G2.Let 1kand 0kbe two vectors of order k with all elements equal to 1 and 0,respectively.Moreover,Jm×ndenotes all m×n ones matrix,and 0m×ndenotes all m×n zeros matrix.

Definition 2.1 The SSG-vertex join of graphs G1and G2,denoted by G1⋆G2,is the graph obtained from the subdivision graphs S(G1)and S(G2)by joining each vertex of V(G1)with each vertex of V(G2).

Note that if we consider the graphs Giwith nivertices and miedges(i=1,2),then the graph G1⋆G2in Definition 2.1 contains n1+m1+n2+m2vertices and 2m1+2m2+n1n2edges.For example,the graphs P2⋆K3is depicted in Figure 1.

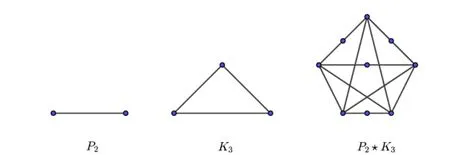
Figure 1

Lemma 2.1[14]LetGbe an r-regular graph with an adjacency matrixAand an incidence matrixR.Letl(G)be its line graph.ThenRRT=A+rEnandRTR=A(l(G))+2En.Moreover ifGhas an eigenvalue equaling to−rwith an eigenvectorX,thenGis bipartite andRTX=0.

Lemma 2.2[14]LetGbe an r-regular graph withspec(G)=r,λ2,···,λn.Then

wherespec(G)is the set of all the eigenvalues ofA(G)together with their multiplicities.AlsoZis an eigenvector belonging to the eigenvalue−2if and only ifRZ=0.

Theorem 2.1LetGibe anri-regular graph withnivertices andmiedges,andAi,Ribe the adjacency matrix and incidence matrix ofGirespectively,wherei=1,2.Then the normalized Laplacian spectrum ofG1⋆G2consists of

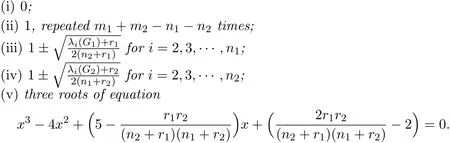
Proof By a proper labeling of vertices,the normalized Laplacian matrix L(G1⋆G2)of G1⋆G2can be written as

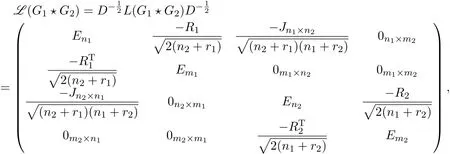
where

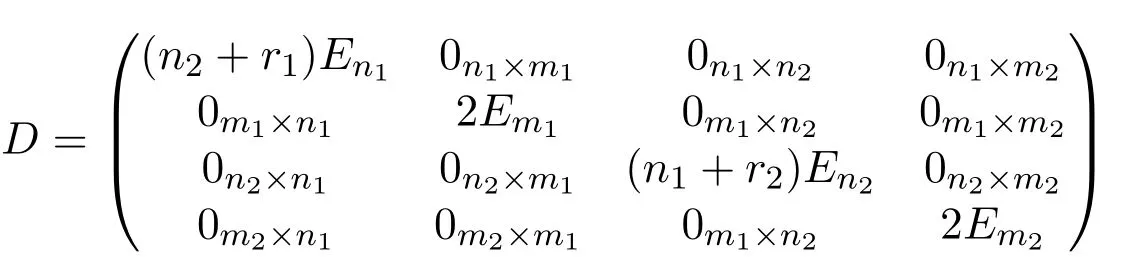
and

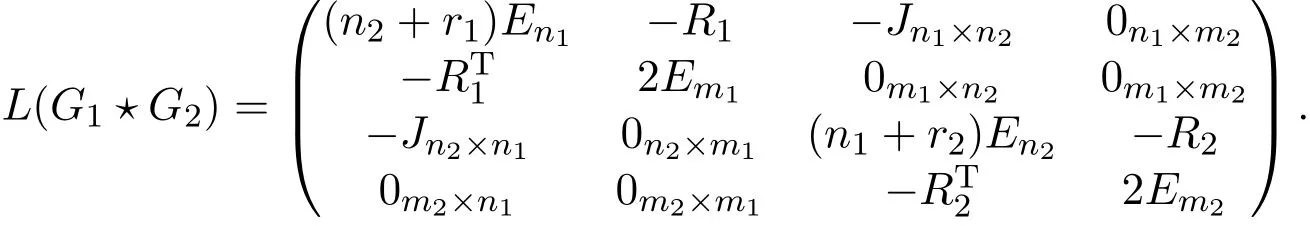
If Giis a regular graph,then Gihas all-one vector 1nias an eigenvector corresponding to eigenvalue ri,while all other eigenvectors are orthogonal to 1ni.

Let X be an eigenvector of G1corresponding to an eigenvalue λi(G1) ≠r1,2 ≤ i ≤ n1,then ϕ =(αX,,0n2×1,0m2×1)Tis an eigenvector of L(G1⋆ G2)corresponding to the normalized eigenvalue θ of graph G1⋆ G2.This is because

This yields

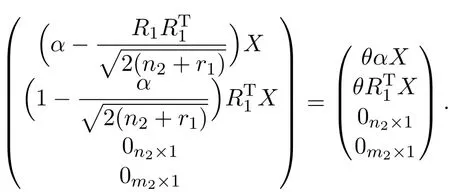
By solving these equations with Lemma 2.1,we get

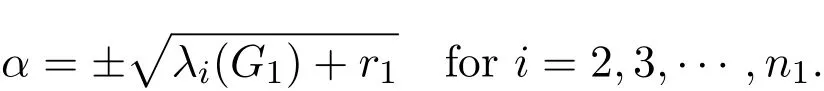
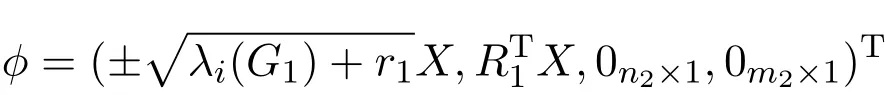
Thus,is an eigenvector of L(G1⋆ G√2)corresponding to the normalized eigenvalue θ of graph G1⋆G2,where θ=1±

Let Y be an eigenvector of G2corresponding to an eigenvalue λi(G2) ≠r2,2 ≤ i ≤ n2,then η =(0n1×1,0m1×1,sY,)Tis an eigenvector of L(G1⋆G2)corresponding to the normalized eigenvalue t of graph G1⋆G2,because

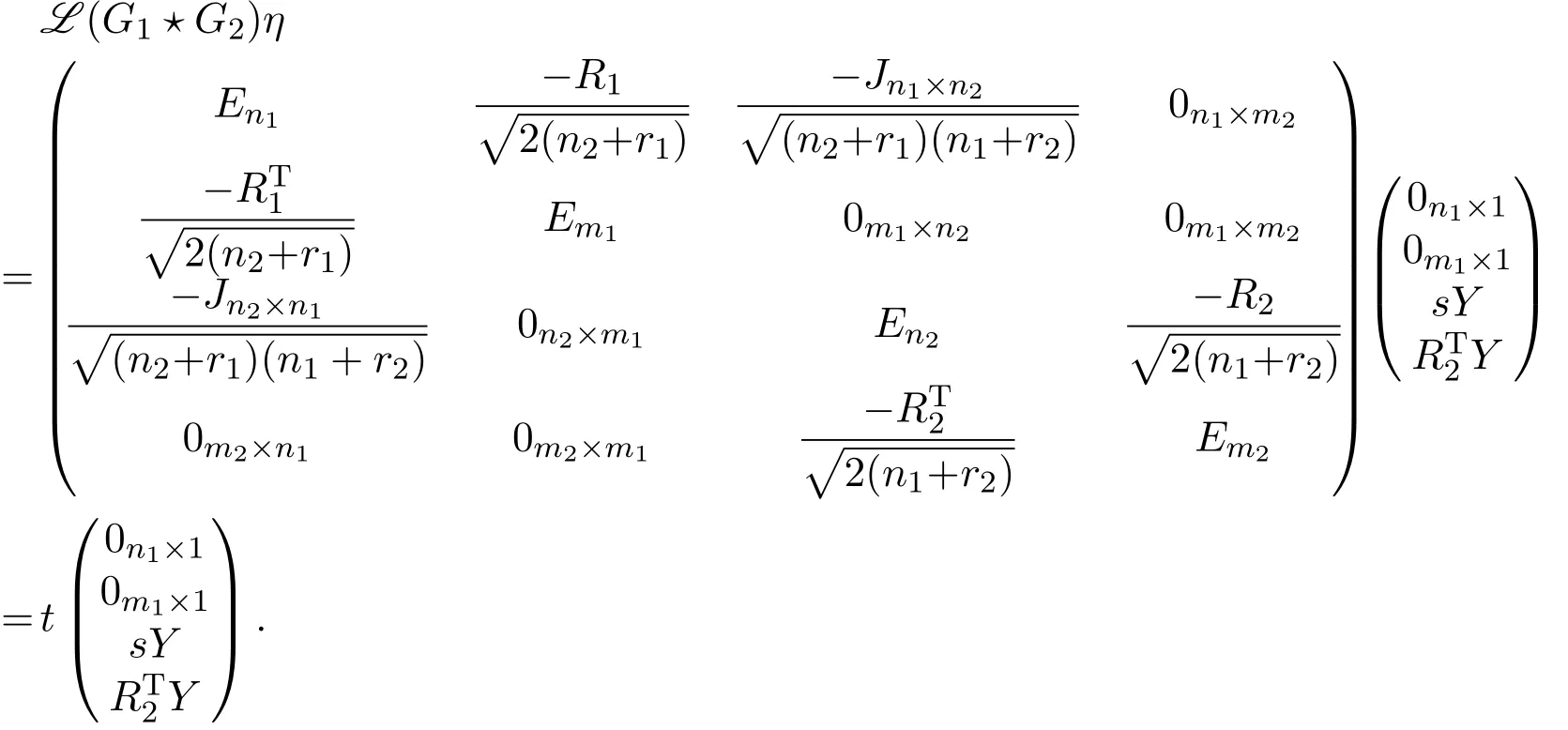
This yields

By solving these equations with Lemma 2.1,we get

Thus,

is an eigenvector of L(G1⋆G2)corresponding to the normalized eigenvalue t of graph G1⋆G2,where t=1±

Now we consider the m1−n1linearly independent eigenvectors Zpof l(G1),whose eigenvalue is−2 and the m2−n2linearly independent eigenvectorsof l(G2)whose eigenvalue is −2,where p=1,2,···,m1− n1,q=1,2,···,m2− n2.By Lemma 2.2,we have R1Zp=0,R2Z′q=0.Hence,γp=(0n1×1,Zp,0n2×1,0m2×1)Tand γq=(0n1×1,0m1×1,0n2×1,)Tare eigenvectors of L(G1⋆G2)with an eigenvalue 1,since

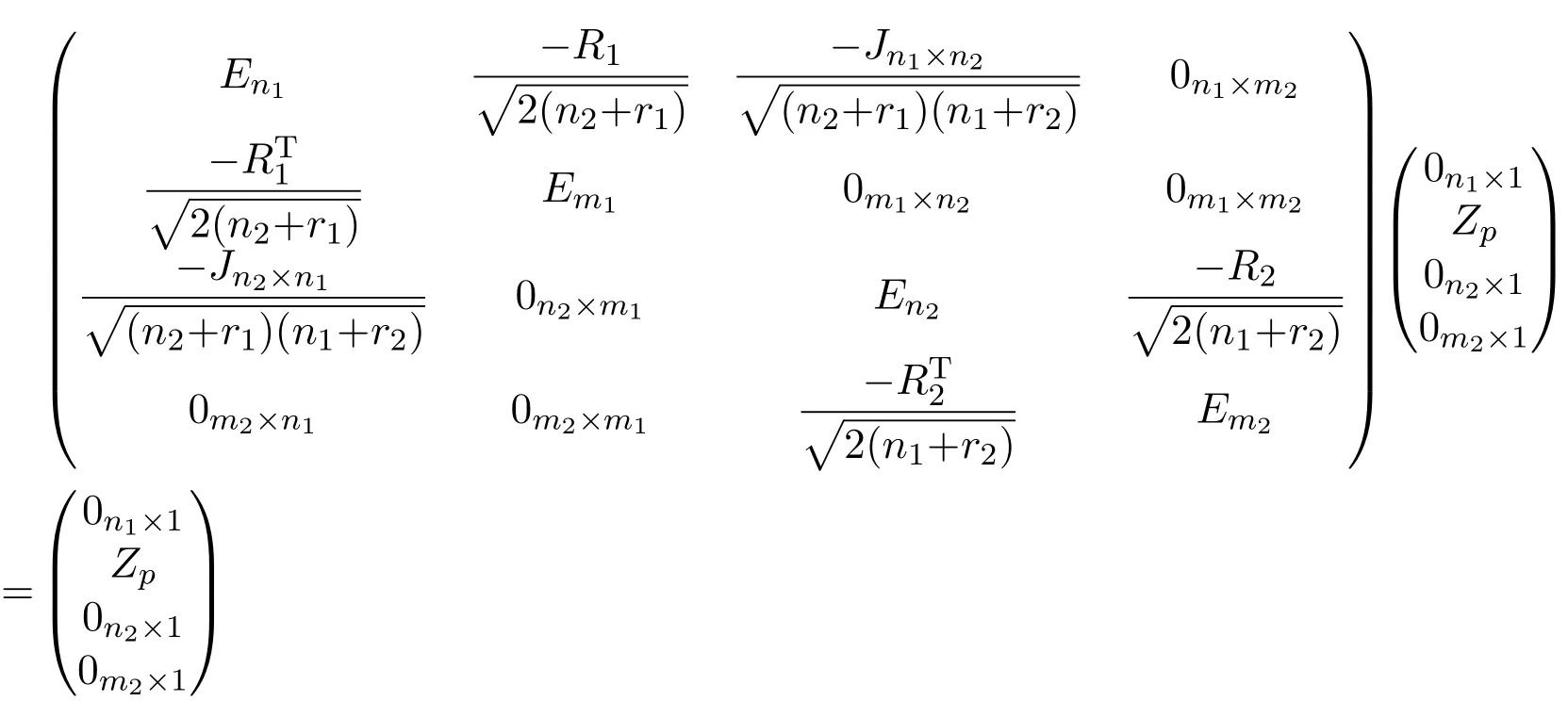
and

From the above argument,we have altogether constructed m1+n1+n2+m2−4 eigenvectors and their eigenvalues.These eigenvectors are linearly independent.Now there remains four eigenvectors.The already constructed eigenvectors are orthogonal to

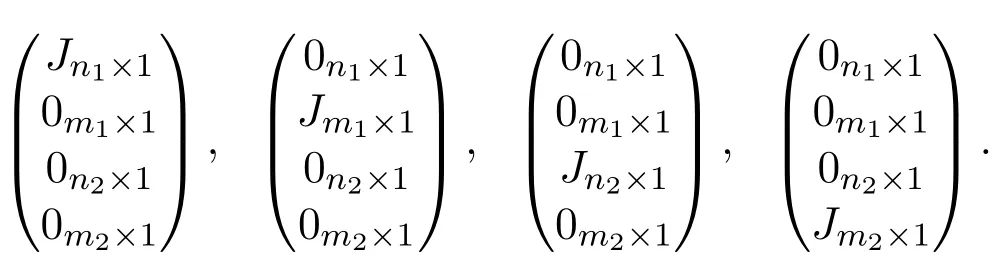
Hence,the remaining four eigenvectors can be spanned by these four vectors,which implies that they are of the form ξ=l1Jn1×1,l2Jm1×1,l3Jn2×1,l4Jm2×1)Tfor(l1,l2,l3,l4)≠0.But then from L(G1⋆ G2)ξ=xξ,ξ is an eigenvector of L(G1⋆ G2)with eigenvalue x if and only if(l1,l2,l3,l4)Tis an eigenvector of the matrix

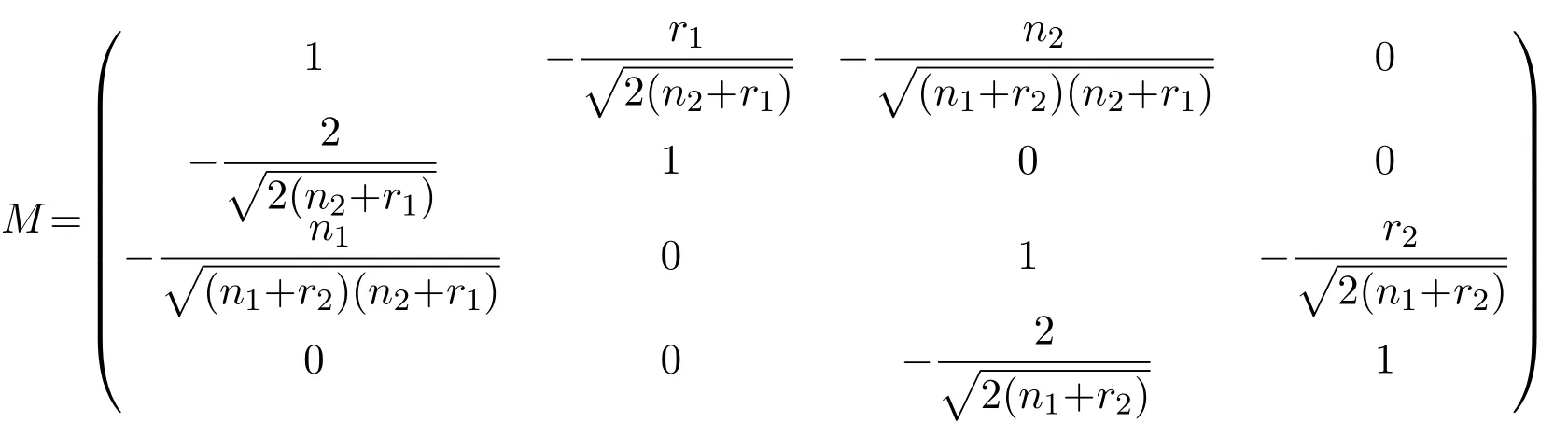
with eigenvalue x.Since the characteristic equation of M is

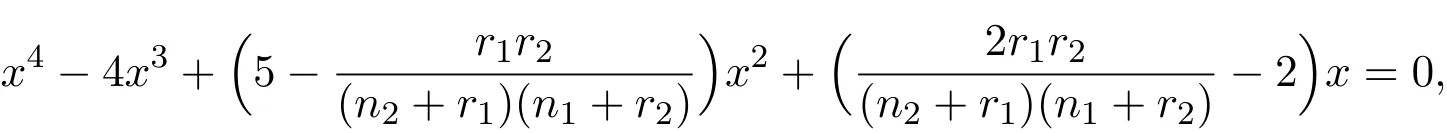
the theorem is proved.

Corollary 2.1IfGis anr-regular graph,andH1,H2are A-cospectral regular graphs,thenG⋆H1andG⋆H2are normalized Laplacian cospectral graphs.

Example 2.1 For any r-regular graph G,the graphs G⋆H1and G⋆H2are normalized Laplacian cospectral graphs,where H1and H2are the graphs in Figure 2.

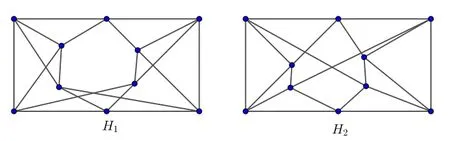
Figure 2:Two nonisomorphic 4-regular which are A-cospectral

The normalized Laplacian energy of G is defined assee[15,16]for details.

Corollary 2.2LetGibe anri-regular graph withnivertices andmiedges,andAibe the adjacency matrix ofGi,wherei=1,2.Then the normalized Laplacian energy ofG1⋆G2is

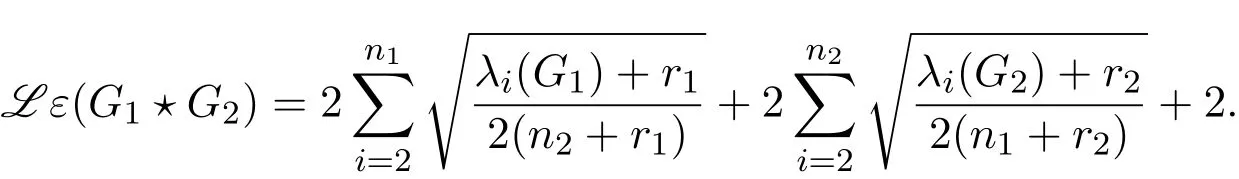
Proof By Theorem 2.1 and the relationship between the coefficients of a polynomial equation and roots,the proof is straight forward.

The degree Kirchho ffindex of graph G is defined by Chen et al.in[19]as

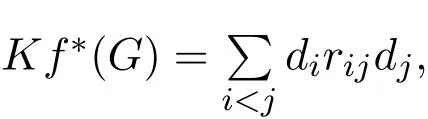
where rijdenotes the resistance-distance between vertices viand vjin a graph G.They proved that,where γi(G)is normalized Laplacian eigenvalues of G of order n,see[17,18]for details.

Corollary 2.3LetGibe anri-regular graph withnivertices andmiedges,andAibe the adjacency matrix ofGi,wherei=1,2.Then the degree Kirchho ffindex ofG1⋆G2is

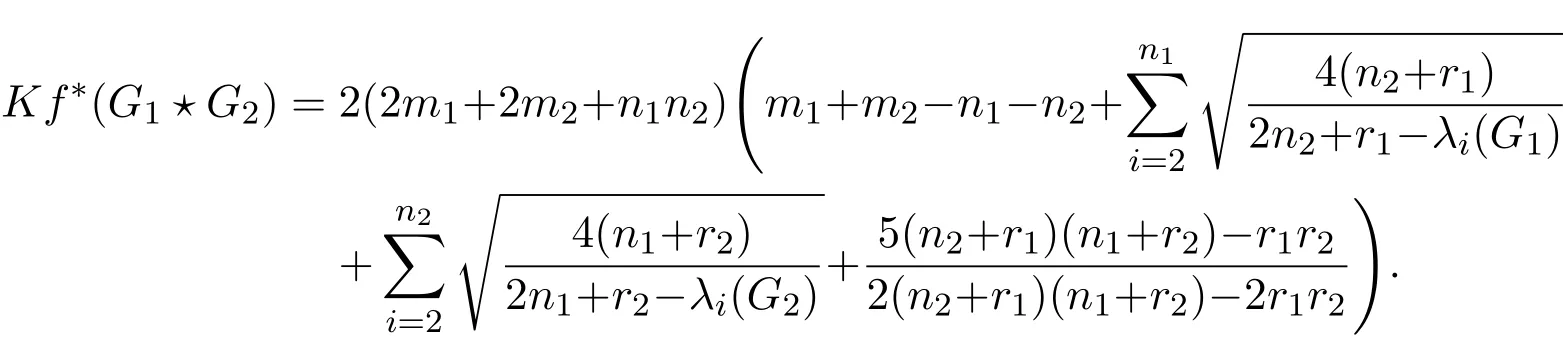
Proof By Theorem 2.1 and the relationship between the coefficients of a polynomial equation and roots,the proof is straight forward.