RAMSEY NUMBER OF HYPERGRAPH PATHS∗
Erxiong Liu
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
Abstract Let H=(V,E)be a k-uniform hypergraph.For 1≤s≤k−1,an s-pathof length n in H is a sequence of distinct vertices v1,v2,···,vs+n(k−s)such that{v1+i(k−s),···,vs+(i+1)(k−s)}is an edge of H for each 0 ≤ i≤ n−1.In this paper,we prove that R(,)=(2n+1)s+1 for n≥3.
Keywords hypergraph Ramsey number;path
1 Introduction
A k-uniform hypergraph H with vertex V is a collection of k-element subset of V.We write K(k)nfor the complete k-uniform hypergraph on an n-element vertex set.For given two k-uniform hypergraphs H1and H2,the Ramsey number R(H1,H2)is defined to be the minimum value of N such that each red-blue coloring of edges ofcontains either a monochromatic red copy of H1,or a monochromatic blue copy of H2.Let H be a k-uniform hypergraph.For each 1≤s≤k−1,an spathof length n in H is a sequence of distinct vertices v1,v2,···,vs+n(k−s)such that{v1+i(k−s),···,vs+(i+1)(k−s)}is an edge ei+1of H for each 0 ≤ i ≤ n −1.We also say that the edges e1,e2,···,enform a path.Similarly,an scycleof length n in H is a sequence of vertices v1,v2,···,vs+n(k−s)such that{v1+i(k−s),···,vs+(i+1)(k−s)}is an edge of H for each 0 ≤ i≤ n−1,v1,v2,···,vn(k−s)are distinct,and vj+n(k−s)=vjfor each 1≤ j≤ s.
When k=2 and s=1,a classical result by Gerencsér and Gyárfás[4]is R(Pn,Pm)=n+for n≥m≥1;it is also known from[2,3]that R(Pn,Cm)=R(Pn,Pm)=n+for n≥m with m being even.Recently,the hypergraph Ramsey numbers also attract lots of attention.When s=1,Haxell et al.[5] first determined that the asymptotic values of R(,),R(,)and R(,)are.Later,Gyárfás,Sárközy and Szemenrédi[6]extended this result to all k≥3.Namely,they proved thatare asymptotically equal to.There are some exact results on short paths and cycles.Gyárfás and Raeisi[7]proved that
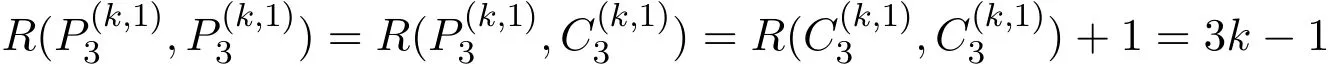
and
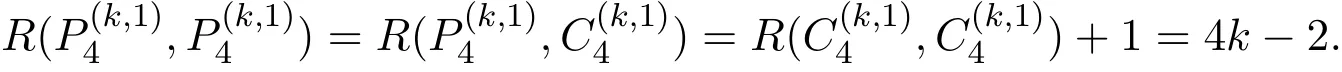
Recently,Omidi and Shahsiah[8]raised the conjecture that
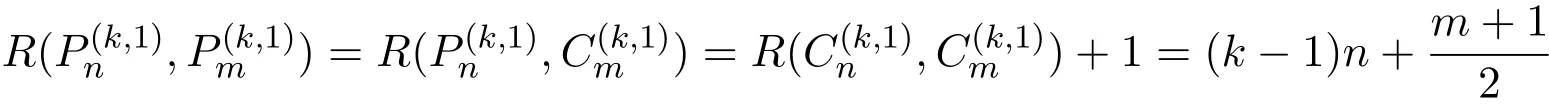
is equivalent to
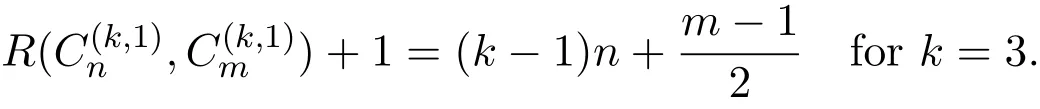
Later,the authors showed that for fixed m≥3 and k≥4 the former is equivalent to(only)the last equality of the latter for any 2m≥n≥m≥3.More precisely,they proved that for fixed m≥3 and k≥4,the latter is true for each n≥m if and only if it is true for the former for 2m≥n≥m≥3.In 2016,Peng[1]proved that for s≥1 and n≥3,
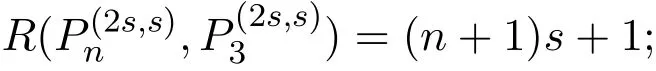
and for s≥1 and n≥4,
A general lower bound is as follows.
Lemma 1[5]For eachn≥m≥1and1≤s≤k/2,we have
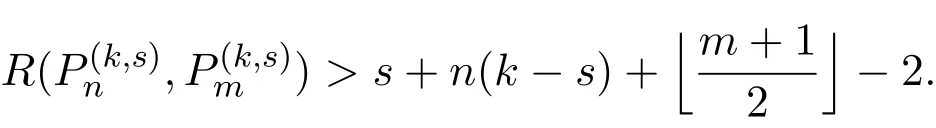
In this paper,we mainly consider the case of k=3s.In order to avoid the excessive use of superscripts,we use the simpler notations
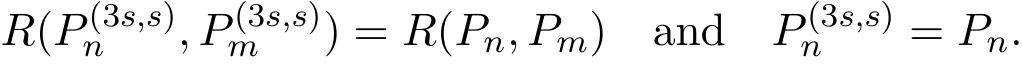
In this note,we have the following result.
Theorem 1For eachs≥1andn≥3,R(Pn,P3)=(2n+1)s+1.
2 Proof of the Main Result
In this section,we dedicate to establish Theorem 1.For convenience,when considering a red-blue edge coloring of,we always denote Hredand Hblueby the hypergraphs that induced by red and blue edges,respectively.
To prove Theorem 1,we need only to prove the upper bound.The proof is by induction on n≥3.We first prove the basis of the induction step,that is R(P3,P3)=7s+1.To this end,we shall establish the following lemmas at first.
Lemma 2For eachs≥1andn≥2,R(Pn,P2)=(2n+1)s.
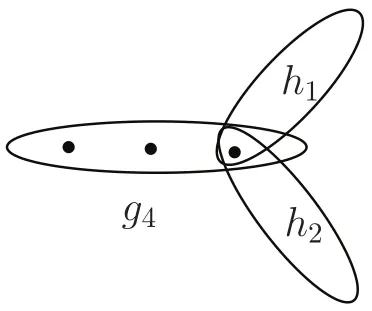
Proof We will prove this lemma by induction on n.For n=2,consider a redblue edge coloring of.We may assume that Hredand Hblueare both nonempty.Let A1∪A2∪A3∈Hred,then Ai∪A4∪A5must be blue for i=1,2,3.Otherwise,they will form a red P2.Meanwhile,the edges A1∪A2∪A4,A1∪A2∪A5,A1∪A3∪A4,A1∪A3∪A5,A2∪A3∪A4and A2∪A3∪A5must be red.Otherwise,it will form a blue P2with Ai∪A4∪A5.Then A1∪A2∪A4and A1∪A3∪A5form a red P2.
For n≥3,we will prove the assertion by induction on n.The base case is n=3.Let c be a red-blue coloring of edges ofon V,where|V|=7s.Since 7s≥R(P2,P2)=5s,there is either a red P2or a blue P2.In the latter case,the assertion holds.Now we consider the former case.Let B and C be the remaining disjoint vertex subsets of V of size s.Consider the edges g1=A5∪B∪C,g2=A1∪B∪A2and g3=A2∪C∪A3.If g1is red,then f1,f2,g1form a red P3.Hence,we may assume g1is blue.Now,if one of g2and g3is blue,then we have a blue P2.Otherwise,g2,g3and f2induce a red P3.
Now let n≥4 and c be a red-blue coloring of the edges inon V,where|V|=N=(2n+1)s.By induction we have R(Pn−1,P2)=(2n−1)s.So there is either a red Pn−1or a blue P2,and we need only to consider the former case.Assume f1,f2,···,fn−1is a red Pn−1,where fi=A2i−1∪ A2i∪ A2i+1,1 ≤ i≤ n − 1,and|Aj|=s,1≤j≤2n−1.Let B and C be the remaining disjoint vertex subsets of V that each of size s.Consider the edges g1=A2n−1∪B∪C,g2=A2j−1∪B∪A2jand g3=A2j∪C∪A2j+1,where 1≤j≤n−2.

Figure 1
If g1is red,then f1,f2,···,fn−1,g1form a red Pn.Hence,we may assume g1is blue.Now,if one of g2and g3is blue,then we have a blue P2.Otherwise,f1,f2,···,fj−1,g2,g3,fj+1,···,fn−1induce a red Pn.The proof is completed.
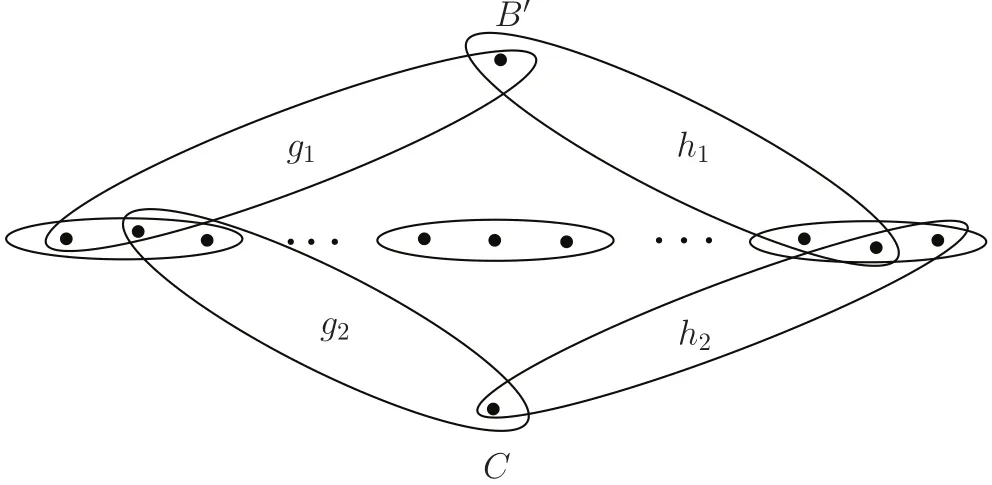
Lemma 3Assume the edgeAi∪Aj∪Akis red for all distincti,j,kwith1≤i,j,k≤2m−1,Ai∪Aj∪Cis red for all1≤i≠j≤2m−1and there is noredPm.For a fixed1≤ t≤⌋,if all edges of type(s+1− t,t− 1,s,s)are blueand there is a blue edge of type(t,s−t,s,s),then there exists a blueP3.
Proof Assume g1is an edge of type(t,s−t,s,s).Letwhere B′is a t-subset of B,is an(s−t)-subset of A2,and i,j,2 are distinct from each other.Chooseto be a(t− 1)-subset of A2.Let
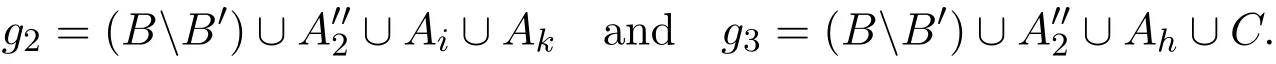
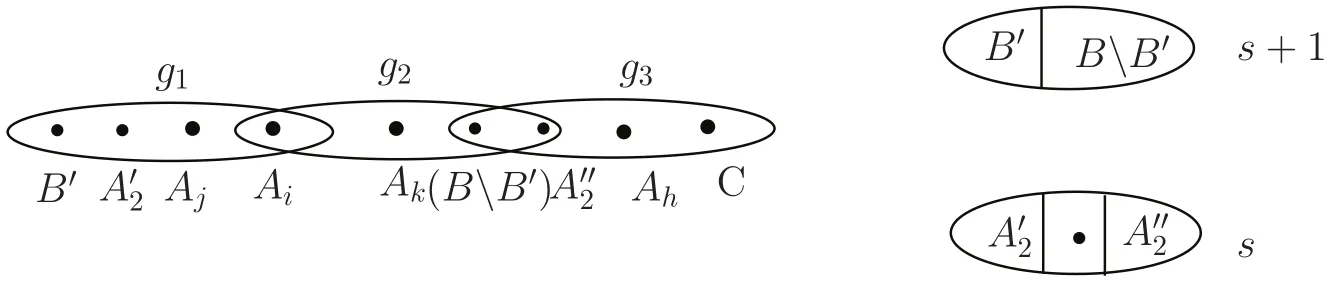
Figure 2
Since both g2and g3are of type(s+1−t,t−1,s,s),by assumption,we have that both g2and g3are blue.Thus g1,g2,g3form a blue P3as desired.The proof is completed.
Lemma 4Assume the edgeAi∪Aj∪Akis red for all distincti,j,kwith1≤i,j,k≤2m−1,Ai∪Aj∪Cis red for all1≤i≠j≤2m−1and there is noredPm.For a fixed1≤ t≤⌋,if all edges of type(t,s− t,s,s)are red,then alledges of type(s−t,t,s,s)are blue.
Proof Suppose to the contrary that g1is a red edge of type(s−t,t,s,s).Let g1=B′∪∪Ai∪Aj,where B′⊆ B with|B′|=s−t,⊆ A2with||=t,and i,j,2 are distinct from each other.We pick an arbitrary t-subset B′′of BB′,and define
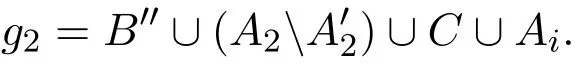
By assumption of this lemma,g2is red since it is of type(t,s−t,s,s).In the following,without loss of generality,we assume i Case 1i=1. If j=2k−1 for 2≤ k≤ m,let g3=A2m−1∪A2k−2∪A3,where g3is red by assumption.Then g2,g1,fk,···,fm−1,g3,f2,···,fk−2form a red Pm,where fi=A2i−1∪ A2i∪ A2i+1,which is a contradiction. Case 2i≠1. If both i and j are odd,thenform a red Pm,here A2m−1∪ A1∪ A3and Ai−2∪ Ai−1∪ Ai+1are red because of the assumption of this lemma,which is a contradiction. If both i and j are even,thenform a red Pm,hereare red because of the assumption of this lemma,which is a contradiction. If i is even and j is odd,thenform a red Pm,here A2m−1∪ A1∪ A3and Ai−1∪ Ai+1∪ Ai+2are red because of the assumption of this lemma,which is a contradiction. If i is odd and j is even,thenform a red Pm,here A2m−2∪ A2m−1A1,A1∪ A3∪ A4and Ai−1∪ Ai+1∪ Ai+2are red because of the assumption of this lemma,which is a contradiction.The proof is completed. The next lemma will tell us that the combination of the above two lemmas gives a blue P3under certain conditions. Lemma 5If the edgeAi∪Aj∪Akis red for all distincti,j,kwith1≤i,j,k≤2m−1,Ai∪Aj∪Cis red for all1≤i≠j≤2m−1and there is no redPm,then there must be a blueP3. Proof We separate the proof into two cases depending on the parity of s. Case 1s is even. We first show that there is at least one blue edge of type(s/2,s/2,s,s).Suppose all edges of type(s/2,s/2,s,s)are red.We pick two disjoint s/2-subsets B′and B′′of B.Letbe an s/2-subset of A2.We define We get g1and g2are red since they are of type(s/2,s/2,s,s).Now,g1,g2,f2,···,fm−1form a red Pm,which is a contradiction.Let j be the smallest integer such that there is a blue edge of type(j,s−j,s,s)for some 1≤j≤s/2.It is easy to see j is well-defined.We observe that all edges of type(s,0,s,s)are blue as if there is no red Pm.Suppose to the contrary that there is a red edge with type of(s,0,s,s).Without loss of generality,let g3=A1∪B′∪C,which is red,then g3,f1,f2,···,fm−1form a red Pm,which is a contradiction.If j=1,then a blue P3is given by Lemma 2 with t=1.If j≥2,then all edges of type(j−1,s−j+1,s,s)are red by the minimality of j for j>j′=j−1.Applying Lemma 4 with t=j−1,all edges of type(s−j+1,j−1,s,s)are blue.Now Lemma 3 with t=j gives a blue P3. Case 2s is odd. If there is a blue edge of type(j,s−j,s,s)with 1≤ j≤,then we repeat the argument similar to Case 1 to get a blue P3.Thus,we may assume that all edges of type(j,s−j,s,s)are red for 1≤ j≤.Using Lemma 4 with t=,we get all edges of type(,,s,s)are blue.Let B′be a-subset of B,andbe two disjoint-subsets of A2.We define where i,j∈/{1,3}.Since g1,g2and g3are of type,by assumption,they are all blue.Hence g1,g2and g3form a blue P3.The proof is completed. Now,we can establish the basis of the induction step. Lemma 6We haveR(P3,P3)=7s+1. Proof Let c be a red-blue coloring of edges of.Since 7s+1≥R(P3,P2),either there is some red P3,or there is some blue P2.We need only to consider the latter case.We assume that f1,f2induce a blue P2,where fi=A2i−1∪A2i∪A2i+1,i=1,2.Suppose to the contrary that there is no blue P3.Let B and C be the remaining disjoint vertex sets of V()with cardinality s+1 and s,respectively.Let B′be an arbitrary s-subset of B.We notice that the edges h1=A1∪B′∪C,h2=A2∪B′∪C,h3=A4∪B′∪C and h4=A5∪B′∪C must be red as there is no blue P3.If the edge Ai∪Aj∪Akis blue for all distinct i,j,k with 1≤i,j,k≤5 and Ai∪Aj∪C is blue for all 1≤i≠j≤5,then a red P3will appear following from Lemma 5.Otherwise,there is at least one red edge Ai∪Aj∪C for some 1 ≤ i≠j ≤ 5 or some edge from Consider the edges g1=A1∪B′∪A2,g2=A2∪C∪A3,g3=A3∪B′∪A4and g4=A4∪C∪A5.Since there is no blue P3,then g1and g2must be at least one red.g3and g4are analyzed in a similar way. Case 1g1and g3are blue. Since there is no red P3,we have that e5,e8and A4∪ B′∪ A5must be blue,otherwise each of these together with g2and h1form a red P3.Similarly,e2,e4and A1∪B′∪A5must be blue otherwise each of these together with g2and h3will form a red P3.Moreover,e1,e3and A1∪B′∪A4must be blue otherwise each of these together with g2and h4will form a red P3.If e6(or e7)is red,then e6(or e7),g4,h1form a red P3,which is a contradiction.Hence,e6and e7must be blue. Since there is also no red P3,A2∪B′∪A3must be blue otherwise this together with g4and h1form a red P3.Similarly,A1∪B′∪A3must be blue.If A2∪B′∪A4is red,then A3∪C∪A5must be blue otherwise this together with A2∪B′∪A4and h1form a red P3.Hence A2∪B′∪A4must be blue.Similarly,A2∪B′∪A5and A3∪B′∪A5must be blue.Let D=C ∪(BB′),then applying Lemma 5 with B=D and B′=C,we get a red P3,which is a contradiction. Figure 3 Figure 4 Case 2g2and g4are blue. This is equivalent to Case 1,we thus omit the proof. Case 3g1and g4are blue. Since there is no red P3,then e1and e3must be blue otherwise each of these together with g2and h4form a red P3.Since there is also no blue P3,then A4∪C∪A5must be red otherwise this together with g1and e3form a blue P3,which is a contradiction. Case 4g2and g3are blue. Since there is neither a red P3,nor a blue P3,we assert that the edges Ai∪Aj∪B′and Ai∪ Aj∪ C are all red with i,j ∈ {1,···,5}{3},otherwise,say A1∪ A5∪ C is blue,then A1∪A5∪C,g2,g3form a red P3,which is a contradiction.Therefore,we can apply Lemma 5 to get a blue P3,which again leads to a contradiction.This completes the proof of Case 4 and hence Lemma 6. Now,we are ready to give the proof of Theorem 1. Proof of Theorem 1 We will prove the theorem by induction on n.The base case is n=3,we have just established in Lemma 6. Now,assume the assertion holds for all 3≤n≤m−1 with m≥4.Consider a red-blue coloring of edges in.Since(2m+1)s+1≥ R(Pm−1,P3)=(2m−1)s+1,by the inductive hypothesis,either there is a red Pm−1or there is a blue P3.We need only to consider the case in which the maximum length of a red path is m − 1.Let f1,f2,···,fm−1be a red Pm−1,where fi=A2i−1∪ A2i∪ A2i+1for 1≤i≤m−1.Let B and C be the remaining disjoint vertex sets of V with cardinality s+1 and s,respectively.Let B′be an arbitrary s-subset of B.Since there is no red Pm,the edges A1∪ B′∪ C,A2∪ B′∪ C,A2m−2∪ B′∪ C and A2m−1∪B′∪C must be blue.If the edge Ai∪Aj∪Akis red for all distinct i,j,k with 1≤i,j,k≤2m−1,and Ai∪Aj∪C is red for all 1≤i≠j≤2m−1,then there exists a blue P3by Lemma 5.Otherwise,consider the edges g1=A1∪B′∪A2,g2=A2∪C∪A3;h1=A2m−3∪B′∪A2m−2,h2=A2m−2∪C∪A2m−1.Since there is no red Pm,one of g1and g2must be red.Similarly,one of h1and h2must be red. Figure 5 Case 1g1and h1are blue. One of A2m−3∪A2m−2∪A1and A2m−2∪B′∪A2m−1must be blue,otherwise,g2,f2,···,fm−2,A2m−3∪ A1∪ A2m−2,A2m−2∪ B′∪ A2m−1form a red Pmwhich is a contradiction.Moreover,one of edges A1∪A2∪ A2m−1,A2∪ A3∪ B′and A2m−3∪A2m−2∪C must be blue. Case 1.1There is a blue edge A1∪Ai∪Ajfor some 2≤i Case 1.1.1i≠2. If j ≠2m−1,then Aj∪Ai∪A1,A1∪A2∪B′,B′∪C ∪A2m−1form a blue P3. If j=2m−1,and i≠2m−3 and i≠2m−2,then A2m−1∪Ai∪A1,A1∪C∪B′,h1form a blue P3. If j=2m−1,and i=2m−3 or 2m−2,then A2∪C∪B′,h1,Ai∪A2m−1∪A1form a blue P3. Case 1.1.2i=2. If j=2m−3 or 2m−2,then A1∪A2∪Aj,h1,B′∪C∪A2m−1form a blue P3. If j ≠2m−3 and j ≠2m−2,then Aj∪A2∪A1,A1∪C∪B′,h1form a blue P3. Case 1.2There is a blue edge A2∪Ai∪Ajfor some 3≤i Case 1.2.1j ≠2m − 1. Then Aj∪Ai∪A2,g1,B′∪C∪A2m−1form a blue P3. Case 1.2.2j=2m−1. If i≠2m − 3 and i≠2m − 2,then A2m−1∪ Ai∪ A2,A2∪ C ∪ B′,h1form a blue P3. If i=2m−3 or 2m−2,then A2∪A2m−1∪Ai,h1,B′∪A1∪C form a blue P3. Case 1.3There is a blue edge A2m−1∪Ai∪Ajfor some 3≤i Then Ai∪Aj∪A2m−1,A2m−1∪C ∪B′,g1form a blue P3. Case 1.4There is a blue edge A2m−2∪Ai∪Ajfor some 3≤i Then Ai∪Aj∪A2m−2,A2m−2∪C ∪B′,g1form a blue P3. Case 1.5There is a blue edge A2m−3∪Ai∪Ajfor some 3≤i Then Ai∪Aj∪A2m−3,h1,B′∪C ∪A2m−1form a blue P3. Case 1.6All the above edges are red,and there exists a blue edge Ai∪Aj∪Akfor some distinct i,j,k with 3≤i In this case,we can consider a new red Pm−1,that is, and we can find a blue P3in the same way as Case 1.3. Case 2g1,h2are blue. The edges A1∪A2∪A2m−1and A2m−1∪A2m−2∪A1must be blue.Otherwise,either A1∪A2∪A2m−1or A2m−1∪A2m−2∪A1is red.For the former case: form a red Pm,which is a contradiction. For the latter case:form a red Pm,which is a contradiction. Case 2.1There is a blue edge A1∪Ai∪Ajfor some 2≤i Case 2.1.1i≠2. If j ≠2m−1,then Ai∪Aj∪A1,A1∪A2∪B′,B′∪C ∪A2m−1form a blue P3. If j=2m−1 and i≠2m−2,then A2∪B′∪A1,A1∪Ai∪A2m−1,A2m−1∪C∪A2m−2form a blue P3. Case 2.1.2i=2. Since A1∪ A2∪ A2m−1is blue from the above discussion,we have j ≠2m − 1.Moreover,if j≠2m−2,then Ai∪A2∪A1,A1∪B′∪C,C ∪A2m−2∪A2m−1form a blue P3. If j=2m−2,we will discuss it in Case 2.5. Case 2.2There is a blue edge A2∪Ai∪Ajfor some 3≤i Case 2.2.1j ≠2m − 1. Then Ai∪Aj∪A2,A2∪A1∪B′,B′∪C ∪A2m−1form a blue P3. Case 2.2.2j=2m−1. If i≠2m−2,B′∪ A1∪A2,A2∪ Ai∪A2m−1,A2m−1∪C ∪A2m−2form a blue P3. If i=2m−2,we will discuss it in Case 2.5. Case 2.3There is a blue edge A2m−1∪Ai∪Ajfor some 3≤i Then Ai∪A2m−2∪A2m−1,A2m−1∪C ∪B′,B′∪A2∪A1form a blue P3. Case 2.4There is a blue edge A2m−2∪Ai∪Ajfor some 3≤i Case 2.5All of the above edges are red,and there exists a blue edge Ai∪Aj∪Akfor some distinct i,j,k with 3≤ i In this case,we can consider a new red Pm−1,that is, and we can find a blue P3in the same way as above case. Case 3g2,h1are blue. Case 3.1There is a blue edge A1∪Ai∪Ajfor some 2≤i Case 3.1.1j=2m−1. If i≠2m − 3 and i≠2m − 2,then A2m−1∪ Ai∪ A1,A1∪ C ∪ B′,h1form a blue P3. If i=2m−3 or i=2m−2,then A2∪C ∪B′,h1,Ai∪A2m−1∪A1form a blue P3. Case 3.1.2j=2m−2. If i≠2m −3,then A1∪Ai∪A2m−2,h1,B′∪ C ∪A2m−1form a blue P3. If i=2m−3,then g2,C∪B′∪A2m−2,A2m−2∪A2m−3∪A1form a blue P3. Case 3.1.3j=2m−3. Then A1∪Ai∪A2m−3,h1,B′∪C ∪A2m−1form a blue P3. Case 3.1.4j≤2m−4. Then Aj∪Ai∪A1,A1∪C∪B′,h1form a blue P3. Case 3.2There is a blue edge A2∪Ai∪Ajfor some 3≤i Case 3.2.1i≠3. Then Aj∪Ai∪A2,g2,C∪B′∪A1form a blue P3. Case 3.2.2i=3. If j≠2m−3 and j≠2m−2,then h1,C ∪B′∪A2,A2∪A3∪Ajform a blue P3. If j=2m−3 or 2m−2,then A2∪A3∪Aj,h1,B′∪C∪A1form a blue P3. Case 3.3There is a blue edge A3∪Ai∪Ajfor some 4≤i Then Aj∪Ai∪A3,g2,C∪B′∪A1form a blue P3. Case 3.4There is a blue edge A2m−3∪Ai∪Ajfor some 4≤i Then Aj∪Ai∪A2m−3,h1,B′∪C ∪A2m−1form a blue P3. Case 3.5There is a blue edge A2m−2∪Ai∪Ajfor some 4≤i Then Ai∪Aj∪A2m−2,A2m−2∪C ∪B′,g2form a blue P3. Case 3.6There is a blue edge A2m−1∪Ai∪Ajfor some 4≤i Then Ai∪Aj∪A2m−1,A2m−1∪C ∪B′,g2form a blue P3. Case 3.7All the above edges are red,and there exists a blue edge Ai∪Aj∪Akfor some distinct i,j,k with 4≤i In this case,we can consider a new red Pm−1,that is, and we can find a blue P3in the same way as Case 3.1. Case 4g2,h2are blue. This case is similar to Case 1.The proof of Theorem 1 is completed now.
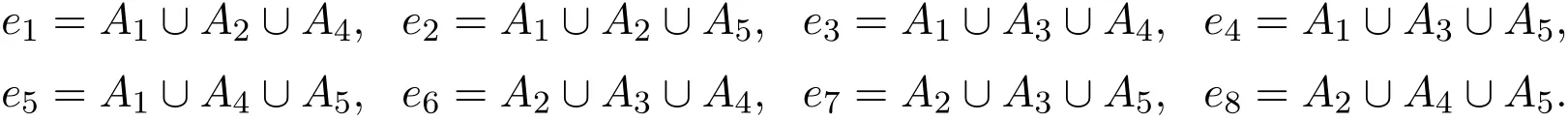

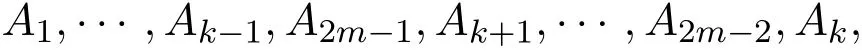

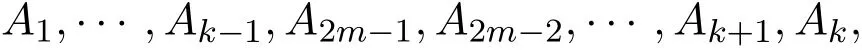
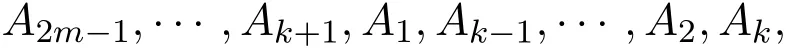
 Annals of Applied Mathematics2018年4期
Annals of Applied Mathematics2018年4期
