解析几何综合题的快速解题研究

摘 要：“直线与圆锥曲线的位置关系”是高中数学解析几何的重要内容，此部分内容的特点是思维量与运算量大，对学生的能力要求很高.本文着重解决“直线与椭圆位置关系” “直线与双曲线位置关系”问题，把它们整合起来，形成模型.与传统做法相比，此优化创新有两个方面的优势：一是提高学生解题速度;二是保障学生解题的准确性.

关键词：解析几何;综合题;快速解题

作者简介：刘坤成（1968-），男，湖北恩施人，本科，高级教师，研究方向：数学教育与数学创新应用.

“直线与圆锥曲线位置关系”是高中数学解析几何的重要内容，特别是“直线与椭圆或双曲线位置关系”是高考的重要考点，也是学生最怕的知识点.特别是此部分内容运算量大，运算能力稍差的学生一般都算错，每次考试该题得分率都很低，久而久之学生就会惧怕此题.

对于“直线与圆锥曲线位置关系”问题，传统的解题模型是以“联立方程组，消元化为一元二次方程，韦达定理代换”为基石，然后结合“判别式”，解决常见的十个方面的问题.其中，直线与椭圆有两个模型（焦点在不同坐标轴上）、直线与双曲线有两个模型（焦点在不同坐标轴上），这四个模型是解决问题的基石，但是这四个模型规律性不强，容易混淆，不易掌握.为了解决这个问题，提高学生解题速度与准确性，本人通过研究与实践，把上面四个模型整合成为一个模型，便于掌握，可使得学生解答此题时既快又准，不易出错.更为关键的是减轻了学生的负担.

1 直线与圆锥曲线位置关系的整合模型介绍

直线用标准式Ax+By+C=0，椭圆与双曲线合二为一也写成标准式x2a2±y2b2=1.整合后的模型总共包含以下三个方面内容.

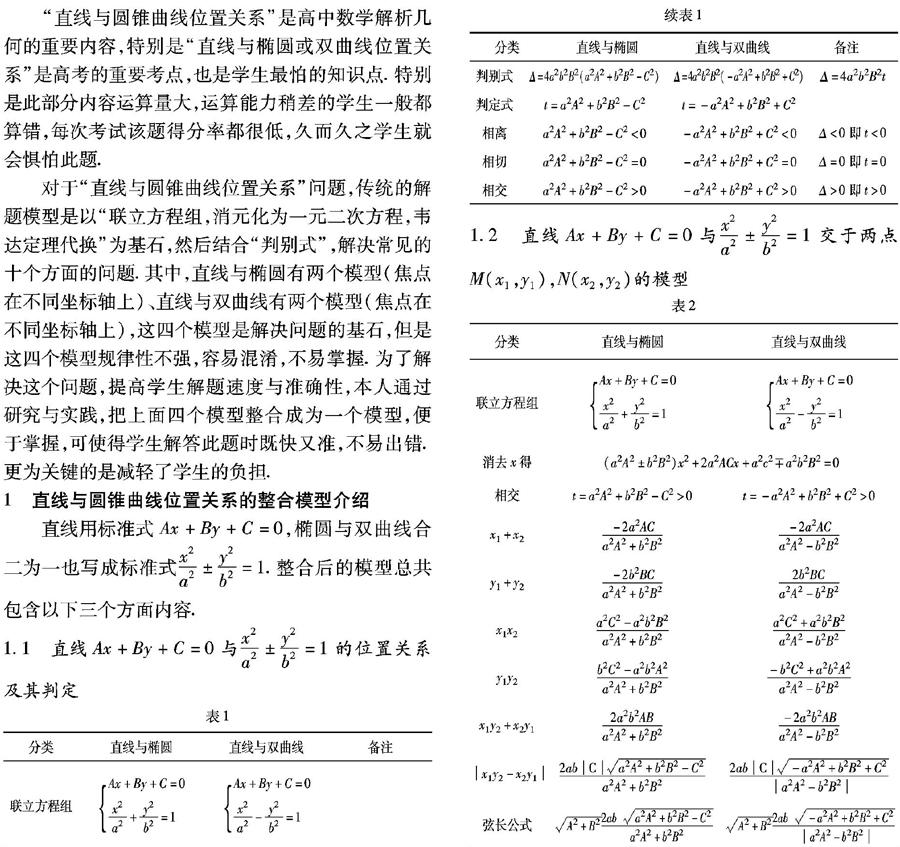
1.1 直线Ax+By+C=0与x2a2±y2b2=1的位置关系及其判定

1.2 直线Ax+By+C=0与x2a2±y2b2=1交于两点M（x1，y1），N（x2，y2）的模型

1.3 最值快解模型

对于弦长公式，有变形

MN=A2+B22aba2A2+b2B2-C2a2A2+b2B2-C2+C2=2abA2+B2tt+C2.

對于椭圆（设中心为点O），任意直线与椭圆交于两点M，N，则ΔOMN的面积的最大值为定值ab2，即

SΔOMN=12MN·d=abCa2A2+b2B2-C2a2A2+b2B2-C2+C2=abCtt+C2≤ab2.

上面就是相关的模型介绍，这是解决“直线与椭圆或双曲线位置关系”问题的基石.

2 直线与圆锥曲线位置关系的整合模型的释义与掌握方法

提出“判定式”概念.在“直线与椭圆位置关系问题”中把t=a2A2+b2B2-C2称为判定式，用于判定直线Ax+By+C=0与椭圆x2a2+y2b2=1的位置关系;在“直线与双曲线问题”中把t=-a2A2+b2B2+C2称为判定式，用于判定直线Ax+By+C=0与双曲线x2a2-y2b2=1的位置关系.

把“直线与椭圆交于两点问题”与“直线与双曲线交于两点问题”整合成为一个问题，使韦达定理结论x1+x2，x1x2，y1+y2，y1y2以及其他如x1y2+x2y1，x1y2-x2y1，弦长公式等全部公式化，成为一项实用性强的成果.

不要看上面的式子复杂，其实规律性极强，容易掌握，极易记忆.

其中一部分式子是优美的对称式，体现了数学的对称美，比如椭圆的判定式t=a2A2+b2B2-C2与x1y2+x2y1=2a2b2ABa2A2+b2B2.

对于其他式子，则用递进的方法掌握.观察“直线与椭圆交于两点问题”的式子，它们的分母全部一样，对称、优美，易于掌握.对于分子，从整体上只需先掌握“直线与椭圆交于两点问题”的两个式子x1+x2=-2a2ACa2A2+b2B2与x1x2=a2C2-a2b2B2a2A2+b2B2，掌握这两个以后，式子y1+y2，y1y2只需在上面的两个式子基础上变换——同时交换A与B，a与b即可.

对于“直线与双曲线交于两点问题”的式子x1+x2，x1x2，y1+y2，y1y2只需把“直线与椭圆交于两点问题”的式子x1+x2，x1x2，y1+y2，y1y2进行变换——把对应的b2换成-b2即可.

弦长公式稍难一点.

学生掌握了公式，就可以直接代公式，减少运算出错，这就解决了大多数学生运算错误问题，还提高了解题速度与解题准确性.

3 直线与圆锥曲线位置关系的整合模型的实践论证

“实践是检验真理的唯一标准”，这个整合结论是否有提高学生运算速度、运算准确度的效果，必须用事实说话.试验所有内容、数据如下.

实践设计 让学生做同一个题，但用不同的方法，比较解题时间与准确性.

实践方法 把学生随机分为两组，分别用传统方法（即目前教材及所有高中复习资料的方法）和上面整合后的模型方法来做，比较做题的时间与准确性.

试题设计 已知椭圆x29+y24=1.

（1）过点（0，5）的直线与椭圆交于两点M，N，求直线斜率的取值范围;

（2）过点（0，5）的直线与椭圆交于两点M，N，求ΔOMN的面积的最大值，其中O是坐标原点.

实验数据 每小问赋分12分.

实践结论

用整合方法的学生解题时间短而得分高，用传统方法的学生解题时间长而得分低，这说明整合后的方法比传统方法要快、准.同时要说明的是，题目越复杂，此模型的效果越好，比如，过点（4，5）的直线与椭圆x213+y27=1交于两点M，N，求直线斜率的取值范围.用传统方法运算量特别大，极易算错，而用模型就不存在这个问题.

通过实践以及在班级应用，证明此模型有极大的优越性：适用于基础中等与基础差的学生（也就是绝大部分学生），一是解题速度提高了;二是运算错误没有了.对于基础特好的学生，可以不用此方法.

从快速解题与准确性来说，此模型具有很大的推广价值.

4 反思

从教育上来说，学生虽然解题速度提高了，运算的准确性也提高了，但是，学生的运算能力没有提高.这里只能说提高的是学生的建模思维.

也许有专家问，你既然没有提高学生运算能力，那么建立模型还有意义吗？

对此问题，这里要思考的是：高中阶段解析几何的运算在过去、现在、将来到底有什么作用？绝大部分学生除了应试，有其他作用吗？事实是，至少百分之九十五以上的学生在过去、现在、将来根本不起作用.所以，不管怎么说，对于基础中等与基础差的学生（也就是绝大部分学生），解题速度、运算准确性提高了，就是减轻了学生的负担，就是成功的.

参考文献：

[1]刘坤成.高中数学基本模型[M].武汉：湖北人民出版社，2012.

[2]刘坤成.中学数学精华[M].北京：九州出版社，2015.

（收稿日期：2019-07-25）