辐照蠕变寿命外推方法

胡靖东 轩福贞 张效成 刘长军

华东理工大学承压系统与安全教育部重点实验室,上海,200237

0 引言

核电是人类获得低碳清洁能源的重要来源之一。以提供更安全、可持续和更经济的核能为目标，核电技术至今已发展成熟至第四代。在第四代核电反应堆中，液态金属快中子增殖反应堆(liquid metal fast breeder reactor, LMFBR)(下称“快堆”)技术较为成熟，是最有可能进行大规模商业化建造的四代反应堆之一。核电技术的革新带来核能利用率的提升，同时对结构材料提出了更高要求[1]，辐照影响就是其中的重要一项。针对不同辐照环境下结构材料的损伤和可承载能力变化的研究[2-3]是保证核设施安全的重要部分。奥氏体不锈钢材料以其优异的高温服役性能，以及相对低廉的制造成本，成为快堆内结构件及燃料包壳材料的首选[4]。在国外，针对冷拉硬化奥氏体不锈钢的辐照蠕变和肿胀性能的研究已较为成熟[5]。如何汲取国外经验，加快建立起符合我国材料特性的辐照性能设计参数数据库，是当前快堆设计面临的主要问题之一。

材料的堆内长期服役性能关乎反应堆长期运行的安全。以钠冷快堆为例，堆芯温度约在550℃[6]，在高温压力容器中，长时服役将导致蠕变损伤超过疲劳损伤，成为承压件失效的主因[7]。如何预测材料的长时高温蠕变性能一直是材料测试的难题。利用实验方法可最为准确地获取材料的长时蠕变性能，然而蠕变实验通常需要几年甚至几十年的时间成本，显然不能满足我国快堆设计的紧迫要求。如今较为可行的蠕变寿命外推方法是利用短时加速实验数据拟合曲线，通过该拟合曲线外推得到材料在低应力水平下的蠕变寿命预测数据，从而获得完整的材料蠕变断裂持久强度曲线，为需长服役期的工程结构设计提供参考。较为常见的一种蠕变寿命外推方法是时间-温度参数(time-temperature parameter, TTP)法，典型代表为Larson-Miller参数方程[8]和Dorn参数方程[9]法。利用这些方法能在蠕变机理不发生变化的情况下，根据短时高温加速的蠕变持久强度实验数据外推得到较为准确的长时蠕变持久强度预测数据。一般而言，利用上述方法外推获得的蠕变持久强度数据所对应的蠕变寿命上限不宜超过实验值的3倍。

奥氏体不锈钢材料在快堆内的蠕变不同于堆外蠕变(即热蠕变)，必须考虑辐照对其产生的影响(即辐照蠕变)。这就使得原有的TTP方法不能直接应用于辐照蠕变数据的外推。针对不同的蠕变机理，已有不少理论模型可进行描述[10]。例如，对于高温长时奥氏体不锈钢材料的辐照蠕变问题，MARGOLIN等[11-12]建立的模型从微观物理机制出发，可完整描述辐照蠕变的损伤形成全过程。然而，上述模型涉及的参数多达30余个，难以直接运用到工程设计之中。

本文希望找到一种既考虑辐照影响，又可如同TTP外推方法一样能较为简便地应用于工程实际的长时辐照蠕变寿命外推方法。为此，通过引入量纲一参数——辐照影响系数，建立了基于蠕变寿命外推TTP法的可用于辐照蠕变寿命外推的辐照-时间-温度参数(irradiation-time-temperature parameter, ITTP)法，以此推导了含辐照影响的Larson-Miller参数方程和Dorn参数方程并进行了验证。

1 辐照蠕变寿命外推模型

可用于辐照蠕变寿命外推的ITTP法是蠕变寿命外推法TTP法针对辐照影响的一个修正形式。ITTP法的建立过程与TTP法基本一致，同TTP法，ITTP法也是建立在Arrhenius方程的基础之上，即

(1)

辐照将对稳态蠕变速率产生影响，该影响的强弱除了与材料自身的微观结构因素有关外，还可能与温度T、辐照通量φ有关。将辐照对稳态蠕变速率的影响通过一个函数f体现，则稳态辐照蠕变速率与稳态蠕变速率的关系可写成：

(2)

辐照会导致材料脆化，也会对蠕变延性产生显著影响。考虑利用一个函数g来体现辐照对蠕变延性的影响。同样，辐照对蠕变延性影响的强弱也可能受温度T、辐照通量φ因素的控制，即

εf,i=εfg(T,φ)

(3)

式中，εf,i为辐照蠕变延性。

在推导TTP方法的过程中，一般假设材料蠕变由稳态蠕变过程主导，即

(4)

式中，εf为蠕变延性；tf为蠕变断裂时间，即材料的蠕变寿命。

参考式(4)，可得到类似的辐照蠕变稳态速率与辐照蠕变延性之间的关系，即

(5)

式中，tf,i为考虑辐照的蠕变寿命。

将式(2)～式(5)代入式(1)，可得到考虑辐照的Arrhenis方程：

(6)

新定义一个系数N：

(7)

称N为辐照影响系数，其值等于辐照蠕变速率与蠕变速率的比值除以辐照蠕变延性与蠕变延性的比值，是一个唯象的量纲一参数。将N代入式(6)，可得

(8)

式(8)即是ITTP法的基本方程。可利用式(8)推导含辐照影响系数N的Larson-Miller参数。对式(8)两边取对数，可得

(9)

Larson-Miller参数方程定义参数PLM等于式(9)等号左边，即

(10)

定义材料常数C为

C=lgA-lgεf

(11)

根据上述定义，可根据式(9)得到包含辐照影响的Larson-Miller参数PLM,i方程：

PLM,i=T(lgtf,i+lgN+C)

(12)

同理，还可通过类似的方法得到含辐照影响的Dorn参数θi方程：

(13)

式(12)和式(13)即是利用ITTP法得到的含辐照的Larson-Miller参数方程及Dorn参数方程。当不存在辐照影响时，由辐照影响系数的定义可知，N=1。此时式(12)和式(13)将退化成一般的TTP参数方程形式，且tf,i=tf，即

PLM=T(lgtf+C)

(14)

(15)

式中，PLM为Larson-Miller参数；θ为Dorn参数。

由此可见，ITTP法实质上是TTP法的一种特例。

2 辐照蠕变外推模型的验证与研究

以利用ITTP法得到的包含辐照影响系数的Larson-Miller参数方程(即式(12))为例，验证ITTP外推法的有效性。

利用GetData软件，本文采集了近50年来公开发表于论文中的堆内辐照蠕变实验数据及对照的未辐照纯蠕变数据共245组。WILLIAMS等[13]基于圆棒试样(图1a)给出的经热处理的304不锈钢的辐照持久强度试验数据显示，辐照降低了304不锈钢的蠕变持久强度；而LOVELL等[14]将预先冷变形20%的316CW不锈钢试样制成内压圆管试样(图1b)，在EBR-Ⅱ堆内经4.5×1022neutrons/cm2(E>0.1 MeV)的中子辐照后表现出持久强度未有下降，甚至出现了上升。BLEIBERG等[15]解释这是由于辐照导致的点缺陷“动态硬化”致使蠕变第三阶段推迟出现的结果。然而， UKAI等[16]利用相同的316CW试样在FFTF堆内剂量为2×1023neutrons/cm2(E>0.1 MeV)的辐照蠕变实验则显示了蠕变持久强度的显著降低，且发现在这些实验中经辐照后试样的蠕变第三阶段提前，且辐照蠕变后0.2%工程屈服强度也有所降低。PISARENKO等[17]基于奥氏体不锈钢材料0Kh16N15M3B制成平板试样(图1c)在SM-2堆内经中子辐照通量密度为5×1012neutrons/(cm2·s)(E>0.85 MeV)的辐照蠕变， 结果显示经辐照后材料的蠕变速率出现增大，持久强度出现降低；KISELEVSKII等[18]基于铬镍奥氏体钢03Kh20N45M4B的不同热处理方式获得的03Kh20N45M4BRTs和03Kh20N45M4BCh在AIMA装置中进行了中子辐照通量密度为4.2×1013neutrons/(cm2·s)(E≥1 MeV)辐照蠕变实验，结果也显示出了辐照蠕变速率增大和持久强度降低。

图1 3种不同试样Fig.1 Three different specimens

不同作者给出的实验方案及条件不尽相同，结果也存在差异，甚至相互矛盾，这说明在不同堆内的辐照蠕变机理可能不尽相同。通常来说，不同的辐照蠕变机理需要使用不同的理论模型求解。然而，本文提出的辐照影响参数N仅涉及到宏观参量(应变速率、延性)的唯象变化，并不涉及具体的微观机理。从理论上说，该参数适用于各种辐照蠕变现象的描述。

利用上述数据，考察本文提出的ITTP辐照蠕变寿命外推方法的有效性。可通过观察辐照数据在经辐照影响参数N的调整后是否向未辐照数据汇聚来确定有效性。首先，利用TTP法的Larson-Miller参数给出一张未经参数N修正的蠕变持久强度图作为参考，见图2。图中所有材料参数C均取20。可以看到，未辐照数据和辐照数据出现了分离，同一种材料的辐照数据和未辐照数据在TTP法中没有统一汇聚在一条曲线上。

图2 TTP法Larson-Miller参数与蠕变持久强度关系图Fig.2 The relationship between creep strength and Larson-Miller parameter in the form of TTP

利用ITTP法的Larson-Miller参数方程重新对上述数据进行处理，即参数采用式(12)的辐照修正形式，结果见图3。图3中数据点符号意义同图2。经过辐照影响系数N的修正之后，图中的实心数据点均向同一形状的空心数据点靠近， 即同一材料的未辐照数据和堆内辐照数据汇聚至同一条曲线上，表明通过辐照影响系数的修正，未辐照数据和辐照数据的规律得到了统一，即该方法已成功表征出了辐照对蠕变的影响。

图3 ITTP法的Larson-Miller参数与蠕变持久强度关系图Fig.3 The relationship between creep strength and Larson-Miller parameter in the form of ITTP

辐照影响系数具有明确的定义，它在不同参数方法中的取值应有一致性。为了研究该一致性是否存在，再引入包含辐照影响系数的Dorn参数方程(即式(13))作图，见图4。图4中数据点符号意义同图2，所有N的取值同图3。所有材料的蠕变激活能ΔΗ均为500 kJ/kmol。图4同图3一样，出现了同一图形的实心数据点向空心数据点靠拢的现象，说明在Larson-Miller参数方程中使用的N值同样也在Dorn参数方程中有效。这一结果表明，辐照影响系数具有在不同参数方法下的一致性，是一个与辐照条件、温度相关的材料常数。

图4 ITTP法的Dorn参数与蠕变持久强度关系图Fig.4 The relationship between creep strength and Dorn parameter in the form of ITTP

为了量化表征各参数方法对辐照实验数据的表征能力，本文定义针对辐照实验数据的均方差，其值等于该材料所有辐照实验测值与未辐照数据按不同参数方法拟合二次多项式曲线后给出的预测值的差值的平方的平均值，该值越小，表明该参数方法表征辐照影响的能力越好。表1中，材料1～材料5分别表示03Kh20N45M4BRTs、03Kh20N45M4BCh、0Kh16N15M3B、316CW、304SA； L-M、Dorn分别表示Larson-Miller参数和Dorn参数。由表1可知，TTP方法的均方差值较ITTP方法均高出一个数量级以上，ITTP方法下的含辐照Larson-Miller参数和Dorn参数的均方差相似且均较小。

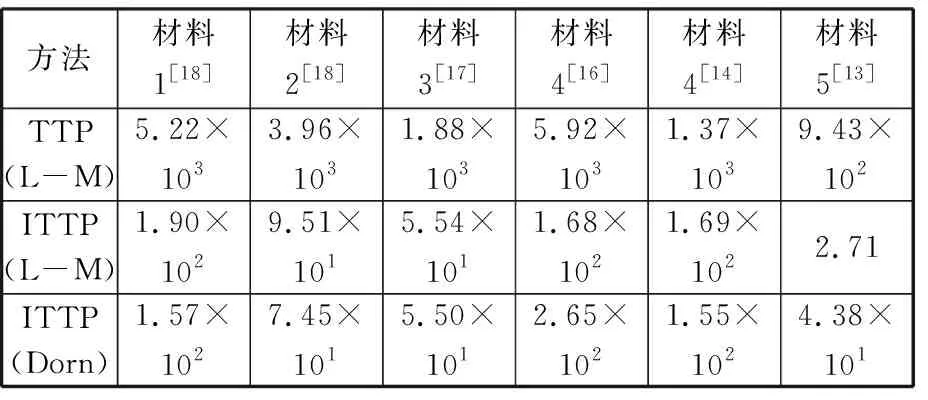
表1 不同奥氏体钢材料的辐照实验数据在各参数拟合法下的均方差

根据辐照蠕变系数在式(12)及式(13)中的位置可知，辐照蠕变系数的增大将导致材料辐照蠕变寿命的缩短。进一步考虑辐照蠕变系数的定义，可知上述关系表明稳态辐照蠕变速率越高，辐照蠕变延性越低，将会导致辐照蠕变寿命变小。辐照蠕变延性的数据分散性较大，显示其较易受外部参数的影响而产生变化，数据整体规律性不强。而稳态辐照蠕变数据则较规律，可用来探究其与辐照蠕变寿命之间的关系。观察图5取自文献[18]的稳态蠕变速率与断裂寿命的实验数据，图中，实线圈内数据为堆内辐照数据，虚线圈内为对照的未辐照蠕变数据，实线圈整体要较虚线圈偏向稳态蠕变速率更大及断裂寿命较小的一边。由此可知，稳态辐照蠕变速率越快，确实存在着使辐照蠕变寿命变小的趋势。这进一步佐证了辐照影响系数这一参数的合理性。

图5 稳态蠕变速率与断裂寿命之间的关系Fig.5 The relationship between static state creep rate and rupture life

辐照影响系数与温度、辐照剂量、材料等因素相关。在现有的数据条件下，由于采集到的数据细节不够充分，研究辐照剂量对辐照影响系数的影响比较困难。而温度对辐照影响系数的影响，可通过上述数据进行初步窥探。如图6所示，不同材料的辐照影响系数与温度的关系并不一致。大体上而言，对于奥氏体不锈钢材料，辐照影响系数随绝对温度的升高呈先下降后逐步趋于稳定的趋势。

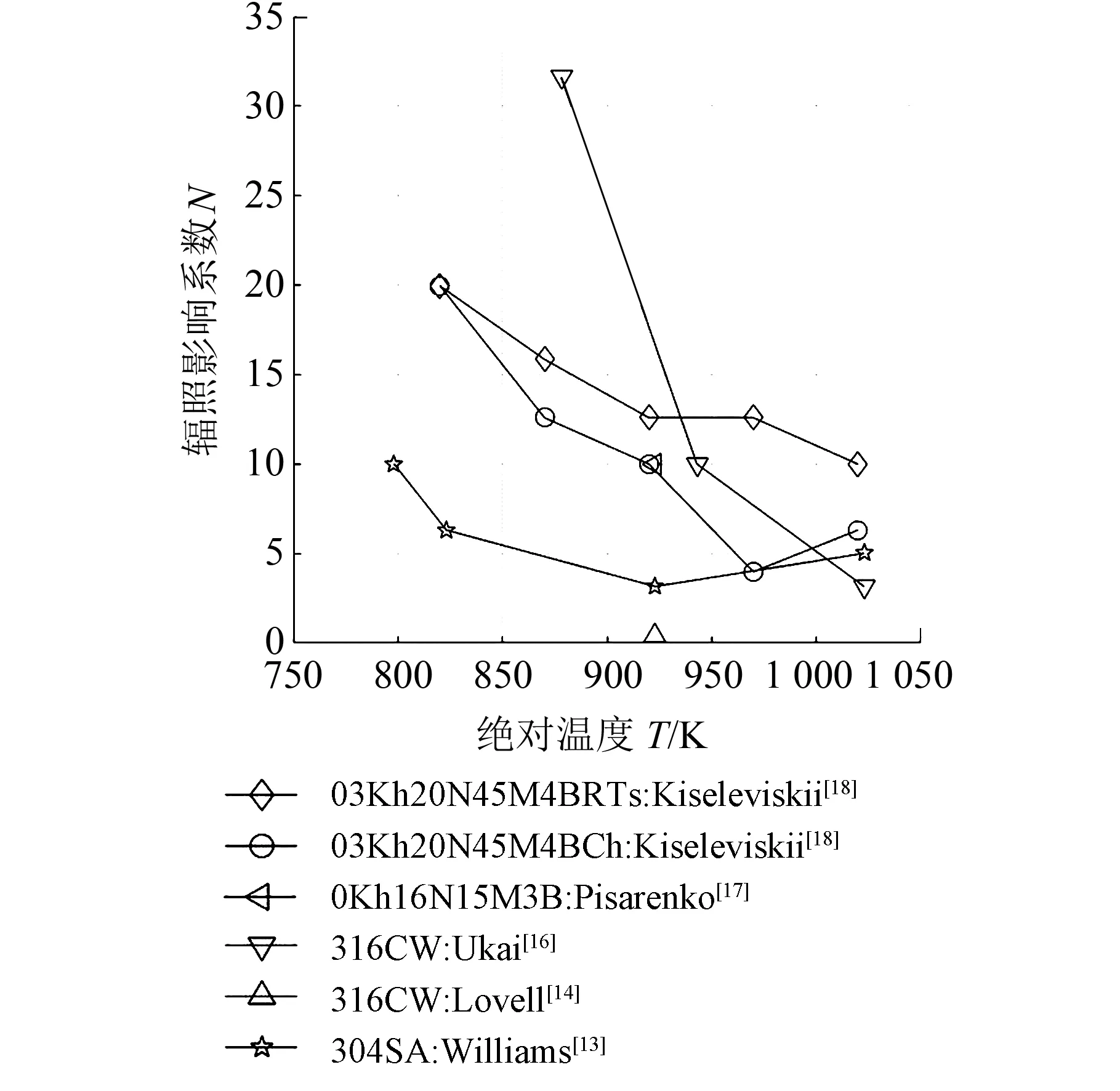
图6 辐照影响系数与绝对温度的关系图Fig.6 The relationship between neutron irradiationin fluence factor and absolute temperature

3 结论

(1)通过引入唯象的量纲一辐照影响系数，改进了高温蠕变寿命外推的常用时间-温度参数(TTP)法，建立了用于辐照蠕变寿命外推的辐照-时间-温度参数(ITTP)法。

(2)在ITTP方法的基础上，推导了含辐照影响系数的Larson-Miller参数方程和Dorn参数方程。

(3)经堆内辐照蠕变数据验证，基于ITTP法的含辐照影响系数的Larson-Miller参数方程和Dorn参数方程均可较好地将未辐照和堆内辐照数据汇聚到一条曲线上。以上结果说明ITTP法的确可表征辐照对蠕变寿命的影响，可用于辐照蠕变规律的拟合和短时辐照蠕变寿命数据的外推。

(4)经验证，本文提出的辐照影响系数具有定常数性质，即采用不同的参数方程时辐照影响系数的值并不会随之改变。

(5)影响辐照影响系数的因素较为复杂，初步研究认为，针对奥氏体不锈钢材料而言，辐照影响系数可能随环境温度的上升而具有先下降后趋于稳定的趋势。