基于伪布尔模型和启发式算法求解无容量设施选址问题

凌海峰

1.合肥工业大学管理学院，合肥，230009 2.过程优化与智能决策教育部重点实验室，合肥，230009

0 引言

无容量设施选址问题(uncapacitated facility location problem, UFLP)是组合优化领域的著名问题之一，经典的应用包括医疗设施选址[1-2]、制造设施选址和物流设施选址等[3]。目前在智慧运输和智慧城市中也有重要的应用，如在城市中如何放置传感器和摄像头来检测交通的拥堵情况。

在UFLP问题中，存在一个设施位置的集合I={1,2,…,m}和一个客户的集合J={1,2,…,n}，每个客户有一个单位需求。 输入数据包括:在位置i(i∈I)建立设施的固定成本向量F(F=(fi));从设施i到客户j(j∈J)的运输成本矩阵C(C=[cij])。 目标是求出一个集合P*(∅⊂P*⊆I), 使得满足所有客户需求的总成本最小。总成本包括建立设施的固定成本以及从设施位置到客户的运输成本。

目前，用于求解UFLP问题的算法大致可分为精确算法和智能优化算法两类。用于求解UFLP问题的智能优化算法主要有遗传算法[4-5]、模拟退火算法[6]、粒子群算法[7]、蚁群算法[8-9]等。这些算法搜索效率高，适合求解大规模问题，但容易陷入局部最优。求解UFLP问题的精确算法主要有分支定界法[10-11]、半拉格朗日松弛法[12]等。这些算法能够发现最优解，但运算速度较慢，通常只适用于小规模的问题。

本文提出利用伪布尔模型和启发式算法来求解UFLP问题。

1 UFLP问题的pseudo-Boolean 表示

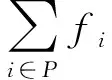
P*∈argmin{f[F|C](P):∅⊂P⊆I}

(1)

首先定义

用向量y=(y1,y2, …,ym)表示任何解P，从而可以用pseudo-Boolean函数将式(1)表示为

y*∈argmin{f[F|C](y)|y∈{0,1}m,y≠I}

(2)

式中，I为单位矩阵。

总成本中的固定成本部分可以表示为

(3)

给定一个m×n维排序矩阵Π=[πij]，它的列向量Πj=(π1j,π2j…,πmj)T定义了一个关于1,2，…，m的排列。对于一个运输成本矩阵C， 所有排序矩阵Π的集合表示为perm(C)，使得cπ1jj≤cπ2jj≤…≤cπmjj(j=1,2，…,n)。

给定一个运输成本矩阵C和一个排序矩阵Π(Π∈perm(C)),对于任意j∈J，可以将运输成本之间的差异表示为

Δc[0,j]=cπ1jj

那么, 对于任意j∈J有

min{cij|i∈P}=Δc[0,j]+Δc[1,j]yπ1j+

Δc[2,j]yπ1jyπ2j+…+Δc[m-1,j]yπ1j…yπ(m-1)j=

这样，对应于一个排序矩阵Π，与解y对应的运输成本部分可以表示为

(4)

根据式(3)和式(4), 对于排序矩阵Π，与实例[F|C]对应的解y的总成本可以用pseudo-Boolean多项式表示：

f[F|C],Π(y)=fF(y)+fC,Π(y)=

(5)

总成本函数f[F|C],Π(y) 对于所有的Π是相同的,称对应于UFLP实例[F|C]和Π的pseudo-Boolean多项式为Hammer函数H[F|C](y)，即H[F|C](y)=f[F|C],Π(y)(Π∈perm(C))。

由式(5)可知，伪布尔表示法用多项式描述了与UFLP问题实例的解对应的总成本，包括实例中的固定成本和运输成本，由pseudo-Boolean多项式容易得出在任何给定位置建立设施对于总成本的影响，这不仅有利于构建预处理规则来降低问题的规模，而且利用pseudo-Boolean多项式中的信息可以设计有效的分支准则来求解问题。

2 基于Khumawala规则和启发式分支准则的算法

算法使用Khumawala规则作为初始阶段的预处理规则，可以通过检查与UFLP实例对应的pseudo-Boolean 多项式或Hammer函数中各决策变量的系数，在分支前确定子问题中某些变量的取值，即在当前的子问题中，确定某些设施能够建立或不能建立。在Khumawala规则不可用时，算法根据Hammer函数中各项系数的特征来预测分支变量，从而设计出问题实例的启发式分支准则。

2.1 Khumawala规则

对于Hammer函数Khumawala规则描述如下：设H(y)是对应于UFLP实例的Hammer函数，其中同类项已经合并。对于每一个设施k, 设ak为对应于yk的线性项的系数，tk为包含yk的所有非线性项的系数之和。那么下面两条规则成立。

上述规则表明，如果Hammer函数中的线性项yi的系数为非负值，则在最优解中，设施i是开放的。同样地，如果在Hammer函数中，包含yi的所有项的系数之和是非正的，则在最优解中，设施i是关闭的。

2.2 分支准则

对于一个|I|=m和|J|=n的UFLP实例，它的解是一个长度为m的向量y，可用 {0,1,#}表示。yj=0 (yj=1) 表示设施j开放(关闭)。yj=#表示设施j还没有确定(开放或关闭)。含有yj=#的解称为部分解，否则称为完整解。

若ak<0,ak靠近0的自由变量yk比ak远离0的自由变量yk在最优解中为0的可能性更大。反之，ak远离0的自由变量yk比ak靠近0的自由变量yk在最优解中为1的可能性更大。

若ak+tk>0,ak+tk靠近0的自由变量yk比ak+tk远离0的自由变量yk在最优解中为1的可能性更大。反之，ak+tk远离0的自由变量yk比ak+tk靠近0的自由变量yk在最优解中为0的可能性更大。

若ak<0且ak+tk>0,设 |ai|=min{|ak|}以及aj+tj=min{ak+tk},ai靠近0的自由变量yi比aj+tj远离0的自由变量yj在最优解中为0的可能性更大。反之，aj+tj靠近0的自由变量yj比ai远离0的自由变量yi在最优解中为1的可能性更大。

类似地，设|ai|=max{|ak|} 以及aj+tj=max{ak+tk}, 那么，ai远离0的自由变量yi比aj+tj靠近 0的自由变量yj在最优解中为1的可能性更大。反之，aj+tj远离0的自由变量yj比ai靠近0的自由变量yi在最优解中为0的可能性更大。

根据上述分析，可得如下分支准则。

(1)最大分支准则：若r=argmax{-ak,ak+tk}, 则从自由变量集合中选择自由变量yr作为分支变量。

(2)最小分支准则：若r=argmin{-ak,ak+tk},则从自由变量集合中选择自由变量yr作为分支变量。

2.3 算法的执行

首先定义HammerFunction和PartialSolution两个过程来应用Khumawala规则。图1中的过程HammerFunction取增广矩阵[F|C]作为输入，返回pseudo-Boolean多项式。图2中的过程PartialSolution以Hammer函数为输入，重复执行Khumawala规则, 直到不能再应用Khumawala 规则作进一步的预处理为止。

图1 构建Hammer函数的伪代码Fig.1 Pseudocode for construction of Hammer function

图2 执行Khumawala规则的伪代码Fig.2 Pseudocode for execution of Khumawala rule

图2中的过程PartialSolution 返回的解一般情况下是部分解。图3中的过程LargestBranchingVariable(最大分支准则)和SmallestBranchingVariable(最小分支准则)取预处理后的部分解为输入, 返回最好的分支变量。

图3 最大分支准则和最小分支准则的伪代码Fig.3 Pseudocodes for maximum branching criterion and minimum branching criterion

使用最大分支准则(LBA)和最小分支准则(SBA)的两种算法递归执行的伪代码见图4。两种算法都执行了预处理步骤(使用了PartialSolution过程)。

3 在物流配送中心选址中的应用算例

一家制造企业在5个不同的地点进行生产，计划建立一个或多个配送中心，用来存储大量的原材料，然后按照要求将它们配送到生产地点。选择4个位置作为候选的配送中心，配送中心i产生的固定成本以及从配送中心到生产地点的运输成本数据见表1，现需要确定配送中心的位置，以使总成本最小。

图4 两种算法执行的伪代码Fig.4 Pseudocodes for execution of two algorithms

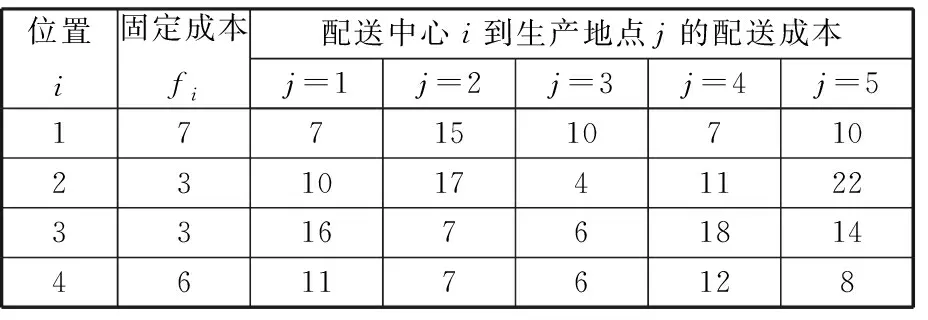
表1 物流配送中心选址问题的数据

下面以LBA算法为例，说明该算法在上述具体问题中的应用。首先建立成本矩阵：

用一个向量y=(y1,y2,y3,y4)来表示任何解P，其中

最优解

y*∈argmin{f[F|C](y)|y∈{0,1}4,y≠I}

总成本中的固定成本

3(1-y2)+3(1-y3)+6(1-y4)

与运输成本矩阵C对应的一个可能的排序矩阵：

与矩阵C对应的运输成本间的差异矩阵

因此，总成本中的运输成本

(7+3y1+1y1y2+5y1y2y4)+(7+0y3+8y3y4+

2y1y3y4)+(4+2y2+0y2y3+4y2y3y4)+(7+4y1+

1y1y2+6y1y2y4)+(8+2y4+4y1y4+8y1y3y4)

于是，总成本的Hammer函数为

[7(1-y1)+3(1-y2)+3(1-y3)+6(1-y4)]+

(7+3y1+1y1y2+5y1y2y4)+(7+0y3+8y3y4+

2y1y3y4)+(4+2y2+0y2y3+4y2y3y4)+(7+4y1+

1y1y2+6y1y2y4)+(8+2y4+4y1y4+8y1y3y4)=

52+0y1-y2-3y3-4y4+2y1y2+4y1y4+

8y3y4+11y1y2y4+10y1y3y4+4y2y3y4

(6)

计算δ+=max{ak}=0。由于δ+≥0,计算r+=min{k:ak=0}=1，因此，可以应用RO规则设置y1=0。将y1=0代入式(6)，可得

H(y)=52-y2-3y3-4y4+8y3y4+4y2y3y4

(7)

ak、tk和ak+tk的值如表2中的a列所示。

如果y3=0,代入式(7)可得

H(y)=52-y2-4y4

(8)

ak、tk和ak+tk的值如表2中的b列所示。

计算δ-=min{ak+tk}=-4。由于δ-≤0,计算r-=min{k:ak+tk=-4}=4。因此，我们应用RC规则设置y4=1。

将y4=1代入式(8)可得

H(y)=48-y2

(9)

ak、tk和ak+tk的值如表2中的c列所示。

表2 ak、tk和tk+tk的值

计算δ-=min{ak+tk}=-1。由于δ-≤0,故计算r-=min{k:ak+tk=-1}=2。由此，可应用RC规则设置y2=1。将y2=1代入式(9)，可得解(0,1,0,1)，成本H(y)=47。由于47<60,设置best=(0,1,0,1),H(best)=47。

如果y3=1,代入式(7)可得H(y)=49-y2+4y4+4y2y4。

类似地，注意到a4=4,可以应用RO规则设置y4=0。从而H(y)=49-y2。

由于a2+t2=-1,可以应用RC规则设置y2=1,从而产生解(0,1,1,0)，成本H(y)=48，由于48>H(best),故最优解y*=(0,1,0,1)，最优成本为H(y*)=47。即在位置1和位置3建立配送中心，最小成本为47。

4 实验结果

本文采用OR-Library中的benchmark实例评价LBA和SBA算法的性能(http://people.brunel.ac.uk/～mastjjb/jeb/orlib/files/)。OR-Library库中有12个中等规模的实例，其中4个实例的规模是m=16和n=50, 4个实例的规模是m=25和n=50, 其余4个实例的规模是m=n=50。

算法使用两个不同的分支准则执行。采用2.20 GHz的Intel i5机器，内存为4 GB。代码使用C++语言，操作系统为Windows 7。

表3中列出了OR-Library中12个benchmark实例的计算结果，包括两种算法计算的最优成本。与文献[9]中的蚁群算法(ACO)进行比较，结果表明LBA算法和SBA算法都能求出benchmark实例的最优解。

表4为使用OR-Library中的12个bench-mark实例进一步对两种算法性能的差异进行比较。实验结果表明，LBA算法要优于SBA算法的执行效果，尤其在较大规模的问题上。如问题实例Cap131， LBA算法的运行时间要远短于SBA算法的时间，表明LBA算法简单高效。

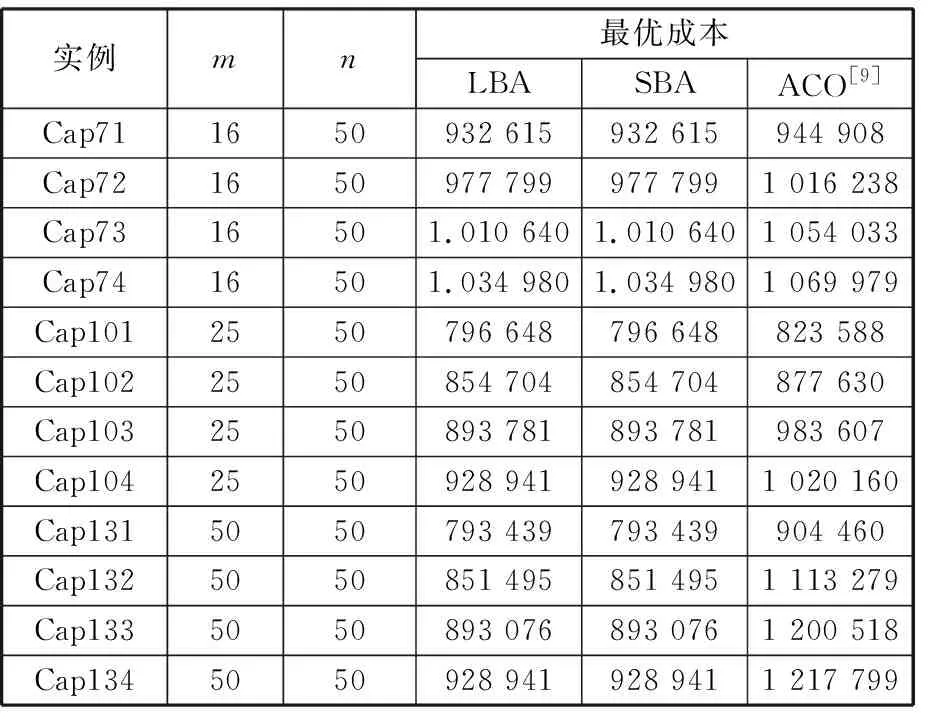
表3 OR-Library中实例的计算结果

表4 LBA算法和SBA算法的性能比较

5 结语

本文在对无容量设施选址问题(UFLP)建立pseudo-Boolean模型的基础上，提出了基于Khumawala规则和启发式分支准则相结合的问题求解方法。从仿真实验结果可以看出，两种新的算法都可以发现问题的最优解。就两种启发式分支准则而言，最大分支准则比最小分支准则能够更加快速有效地解决UFLP问题。今后将进行更广泛的测试并对该方法作适当的改进。此外，将新算法应用到其他组合优化问题也是一个值得研究的方向。