格栅数据的费用分析模型在公路择线求解中的应用
文/江西省赣南公路勘察设计院 欧阳路明 朱艳梅
本文应用基于格栅数据的费用分析模型,探索公路择线的布线经济走廊的产生和选定方法,尝试应用GIS空间数据及其多重分析功能,实现科学化、数据化和图形化的公路择线优化求解。
公路择线的费用分析模型简述
公路择线费用分析模型,是一种智能化的空间数字模拟模型。该模型基于格栅数据和GIS空间数据计算,依靠多重分析功能,对公路最佳择线开展科学化、数据化和图形化的求解。
基于费用模型的公路最佳择线求解
费用分析模型通过模拟格栅和GIS空间数据进行择线分析计算,以此获取最为理想的择线。比如我们假设存在一个非连续的二维空间:
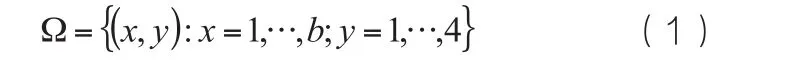
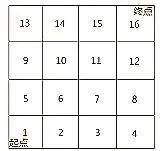
图1 数据格栅基本模型
则数据格栅基本模型,具体如图1所示。其中,起始格栅(1,1)处于该图的左下角,而格栅(4,4)则处于该图的右上角。采用Dijikstra算法分析最佳择线时,最为关键的是要求出权距离,这就涉及了两个不同类型的格栅层,一个是源格栅层,另一个则是费用格栅层。其中,源格栅层涵盖了一个以上的区域,可根据自身情况将这些区域连接,而这些单元都已被赋值。Arcview的GRID模块可通过函数关系对格栅的最佳择线进行计算与分析。比如由COSTDISTANCE函数生成的输出格栅层,主要对距离源格栅最近的费用进行统计与分析。这种算法的最大特点是运用了“节点/联系”模型,将格栅单元看作节点,各单元的距离也就成了权距离。理论上,在水平和垂直方向,格栅单元所形成的权距离为1,而在斜方向就成为了1.414。
对于可在四个方向灵活运动的格栅单元来说,假设从1到2到3时,那么此“联系”值就成为这个格栅单元的费用值与其邻近单元费用值的一个均值,也就是:

式中cost1、cost2分别是单元1、2的值,q是从1到2的一个联结长度。可利用下式求出邻近单元3的累计费用,具体如下:
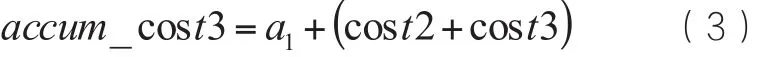
式中,cost2是单元2的值,cost3是单元3的值,accum-cost3是累计费用值。
假设是在斜线方向,从单元1到6到11所形成的这种“联系”也就成为这个格栅单元的费用值与其邻近单元费用值的一个均值的1.414倍,具体如下:
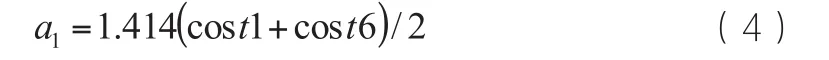
式中cost1、cost6分别是单元1、2的值,q是从1到2的一个联结长度。可利用下式求出邻近单元11的累计费用,具体如下:
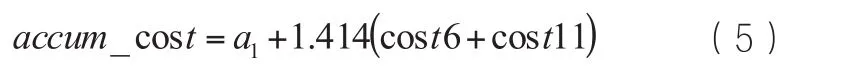
式中,cost6是单元6的值,cost11是单元11的值,accum_cost11则是累计费用值。
通过费用格栅,可计算出各单元到源单元的最低费用。只要计算出累计费用,就能获得到另一目的地最佳择线线。
采用上述介绍的计算方法及具体操作流程,求出与起始格栅有关的全部格栅择线的累计费用,然后确定出邻近格栅的最佳择线顺序,并将其视为链接的重要依据;如果探索出的新择线循环择线未发生任何改变,表明可中断计算程序。
在Arcview的grid的模块中,可利用前文提到的函数根据格栅数据对最佳择线进行分析,具体如下:
第一,构建一个与实际情况相适应的源点格栅sourcegrid,如图2所示,与此同时,还可构建一个容易辨识的终点格栅destingrid,如图3所示。
第二,构建一个格栅图costgrid,用来分析择线费用,如图4所示,通过该图数值可确定费用大小。
COSTDISTANCE的函数表达式如下:

第三,可获取两个不同类型的格栅图,一个是方向格栅“dir_grid”,如图5所示。另一个是方向分配格栅图" alloc_grid"和累计费用图accum_cost图,如图6所示。
COSTPATH的函数表达式如下:

根据计算结果绘制出最佳择线图,如图7所示,从起点(1,1)到终点(4,4)的最佳择线具体为:(1,1)一(2,1)一 (3,1)一 (4,2)一 (4,3)一 (4,4)。
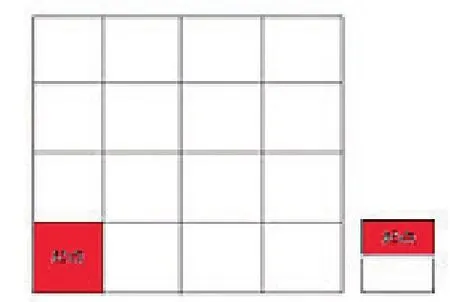
图2 起点格栅图
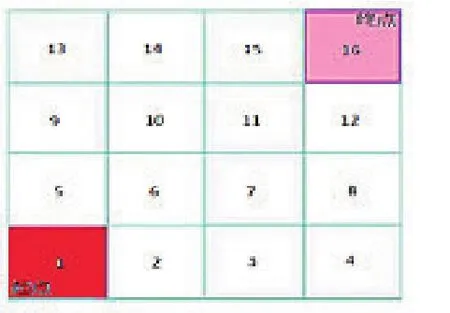
图3 终点格栅图

图4 费用值格栅图
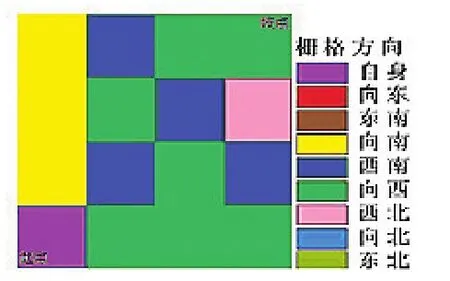
图5 方向格栅图
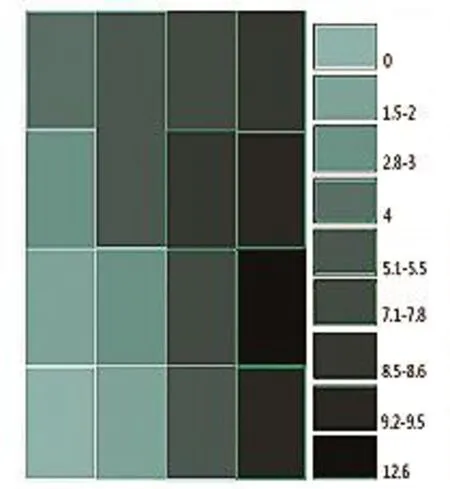
图6 费用累计格栅图
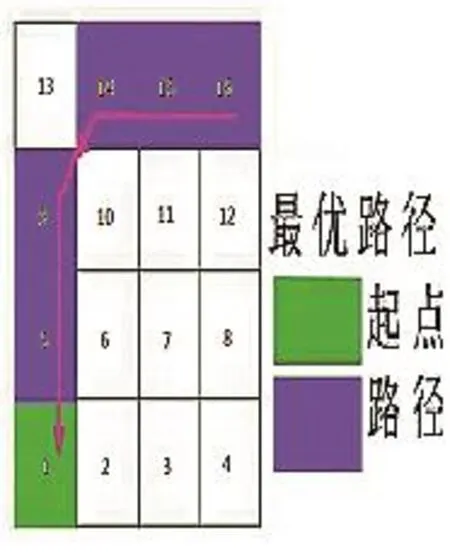
图7 择线结果格栅图
公路择线的布线经济走廊的选定
要想获得最佳公路布线走廊,需完成以下操作:在择线范围内,求出任一点到始点的最小累计费用;在择线范围之内,求出任一点到终点的最小累计费用;将前两步的累计费用计算结果进行叠加运算,由此便可计算出任一点到起点和终点的最小累计费用。
距离最佳择线最近的是布线经济走廊,一般用浅色填充,距离最佳择线越远,颜色就越深,最小累计费用就越高。如何才能确定出最符合现实情况的公路布线经济走廊,可通过以下操作来完成,具体如下:
在选择的区域内,先求出与起点A有关的每个格栅的最小累计费用,可通过下式获得此值:
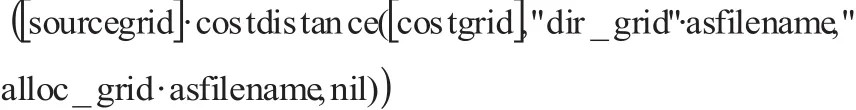
确定出accum_grid和dir_grid这两个性质不一的格栅图。
任一点C到A的最优择线,具体如下:

任一点C到A点的最佳择线区域用蓝线进行标识,同样道理,颜色越深,表明生成的最小的累计费用就越高。
在选择的区域内,求出与终点B有关的每个格栅的最小累计费用,其计算过程可参考步骤1,两者的计算方式完全一样,只是将A更换为B。
在既定范围之内,任一点C到B的最佳择线用黑色进行标识,由白色到绿色的这个演变过程,颜色越深表明产生的最小累计费用就越高。

