基于尾轴-油膜-艉部结构的轴系稳定时间
陈天然, 董良雄, 俞嘉阳
(浙江海洋大学 港航与交通运输工程学院, 浙江 舟山316022)
0 引 言
航行中的船舶受恶劣环境影响,船体在外力作用下会产生不均匀变形与随机运动,造成船体形变,轴系、尾轴承油膜与船体之间相互耦合、相互影响,从而使轴系进入不稳定状态。抑制或削弱船舶轴系振动是加强其工作稳定性和改善传动性能的关键所在。本文应用数值计算,研究了不同载荷、不同转速下船舶轴系稳定性的变化规律,分析其纵向振动的特性并寻求有效方法,以达到缩短碰摩发生后轴系恢复稳定所用时间的目的,希望为船舶建造的优化设计与轴系的合理安装提供一定的理论基础,加强船舶在航行过程中的安全保障。
1 船舶尾轴在外力作用下的稳定性分析
针对船舶尾轴的复杂受力状态,开展其轴心轨迹的瞬变及由瞬变到稳定过程的研究具有重要理论意义和应用价值。船舶尾轴承承受的动载荷形式有2种:一种是冲击载荷,其特点是持续时间非常短暂,能量释放和传递是骤然完成的,在冲击载荷作用下,系统产生瞬态运动,轴心位移发生较大变化;另一种是周期变化的动载荷,最常见的就是碰摩载荷,在其作用下,轴心轨迹发生涡动,轴心轨迹周期变化,轴心轨迹是滑动轴承内部润滑规律的外部表征,是轴承工作状态的综合反映。因此,通过轴心轨迹,可以判断轴承的稳定性,确定轴承的承载能力,判断轴承设计参数的合理性。
按照离散化建模思路,首先将船体艉部结构离散化,使离散化的艉部结构之间具有线性弹性联接,并将尾轴系统简化为单圆盘系统,两端由滑动轴承支撑,建立相应的力学模型[1-3]。绘制的力学模型如图1所示。
具体参数的取值为:m1=100kg;m2=80kg;m3=m4=m5=200kg;c1=c2=c3=5 000N·s/m;k1=k2=5×106;c=0.2mm;r=0.06mm;f=0.1;k3=k4=k5=5×107。
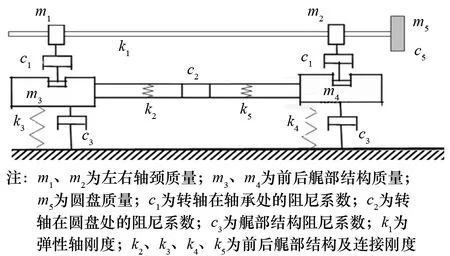
图1 数值模型结构
设系统的质量矩阵、阻尼矩阵、陀螺力矩矩阵和刚度矩阵分别为M、C、J和K,转子系统动力学方程为

(1)

2 冲击载荷下尾轴由扰动到稳定的过程模拟
在正常工况下,轴心轨迹对转速的变化最为敏感,不同转速下轴心轨迹在收敛与发散间变化不定[4-6]。在轴系轨迹是收敛的情况下,发生扰动时,轴心轨迹趋向偏离原来的运动轨迹,一段时间后恢复到稳定状态。在不同扰动下,轴心轨迹恢复的过程和时间都不相同。本文主要分析2种情况下轴心轨迹的变化规律:一种是在冲击载荷工况时不同转速下轴心轨迹的变化;另一种是转子系统存在碰摩载荷工况时,不同转速下轴心轨迹的变化规律。
船舶在航行过程中,螺旋桨和船体受外力作用,常常会对尾轴的运动造成影响,这种影响作用可用冲击载荷来进行描述。冲击载荷作用于轴的矩形脉冲载荷随无量纲时间的变化规律如图2所示。冲击载荷可用式(2)来描述。
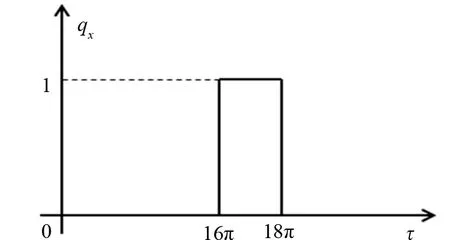
图2 冲击载荷图
(2)
在推进轴系的运动过程中,随着激励频率的增大,系统呈现出由稳定运动过渡到周期运动再到混沌运动的状态,振动系统拓扑结构也会发生相应的改变。本文选取2种轴系工况,即周期运动和混沌运动2种不同转速工况,对应的转速分别为760 r/min和800 r/min,进行分析与模拟,得到其振动轨迹曲线和振幅-时间响应曲线如图3所示。其中,转速为760 r/min时的轴心轨迹如图3a)所示,轴颈振动响应如图3b)、图3c)所示(其中箭头线段表示受到冲击载荷后轴系恢复稳定所需的时间)。

图3 转速760 r/min、800 r/min时轴颈振动响应及轴心轨迹图
由图3分析得出,冲击载荷对轴心轨迹产生一定的扰动影响,且冲击载荷愈强激起的轴系振幅愈大持续时间愈久。转速为760 r/min时的稳定时间为1.2 s,转速为800 r/min时的稳定时间为1.4 s,因此,受到同样冲击载荷时,选择合适的转速可有效缩短轴系受到冲击后的稳定时间。
改变冲击载荷的大小和持续时间,保持轴系转速不变测取尾轴的稳定时间如表1所示。
3 碰摩载荷下的尾轴稳定过程分析
3.1 碰摩载荷下轴心稳定过程模拟
碰摩载荷是船舶营运过程中尾轴与尾轴承发生接触而产生的一种工况。发生碰摩时,尾轴与尾轴承之间既有碰撞产生的径向冲击力,也有轴向摩擦力,该作用力由尾轴承来承受。假设尾轴与尾轴承之间的间隙为δ,碰撞过程为弹性变形,则碰摩力可表示为
(3)
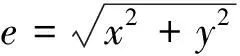
同样,取碰摩摩擦因数为0.1,间隙δ为0.000 2,即保持碰摩载荷的大小不变且作用时间相同,且碰摩装置刚度一定,改变轴系转速,当轴系转速分别为760r/min、800r/min时,测得不同转速条件下轴系恢复稳定所需时间的曲线,结果如图4所示,其中图4a)为转速760r/min时的轴心轨迹图,图4b)和图4c)分别为2种转速下的振动时程图。
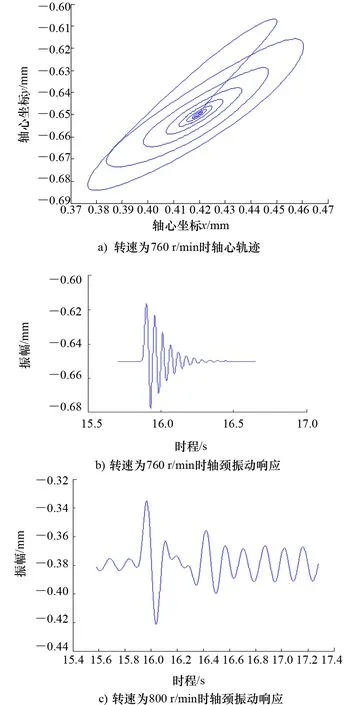
图4 转速为760 r/min、800 r/min,碰摩摩擦因数为0.1,碰摩间隙为0.000 2时轴心轨迹图与轴颈振动响应图
从图4可看出:当船舶轴系碰摩载荷大小和弹簧刚度一定时,船舶轴系转速的改变会对其轴心轨迹的稳定造成一定影响。随着轴系转速的提高,轴承支承油膜力动态特性发生改变,轴系在碰摩载荷作用下引起的扰动振幅较大,振动幅值由小到大,从不碰摩到轻微碰摩,从轻微碰摩到比较严重的碰摩。
另外,碰摩摩擦因数的改变对轴系振动也有一定影响,但不如另外2个参数明显。若碰摩摩擦因数越大,即弹簧刚度越大,则轴系发生碰摩后的纵向振动越剧烈,转子振幅变化越大且曲线变得更不光滑,故在受到同样的碰摩载荷时,适当地调节转速和选择恰当的摩擦因数可有效缩短轴系稳定时间。
3.2 碰摩载荷下的尾轴稳定性比较
为进一步对碰摩载荷作用下尾轴的稳定性进行比较,保持轴系转速不变,通过改变碰摩载荷的摩擦因数和弹性系数,观察稳定时间并进行比较。记录稳定时间并计入表2。

表1 760 r/min时不同载荷下的稳定时间 s

表2 500 r/min时不同载荷下的稳定时间 s
表2的数据可以制作成图5、图6。

图5 稳定时间随弹性系数的变化曲线
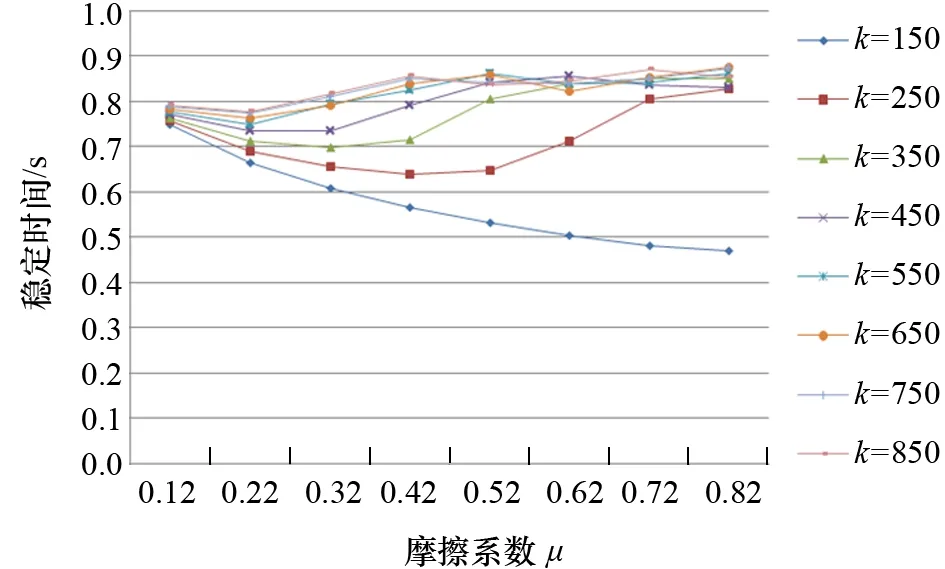
图6 稳定时间随摩擦因数的变化曲线
图5是摩擦因数一定,稳定时间随弹性系数的变化曲线。图中x轴为弹性系数,不同标记的折线表示各摩擦因数下的变化趋势。由图5可知,在相同的摩擦因数下,当轴系的弹性系数不同时,轴系恢复稳定所需时间呈现不同的变化特性。
图6是弹性系数一定,随着摩擦因数的增大,稳定时间的变化曲线,可看出在不同摩擦因数下稳定时间增速不同,摩擦因数越低,稳定时间增速越小,甚至呈上升趋势。例如,弹性系数为150时恢复速度最快,曲线最光滑。当摩擦因数较小时,弹性系数较低则轴系恢复稳定所需时间较大;当摩擦因数较大时,弹性系数越高则轴系恢复稳定所需时间越大。
4 结 论
本文以船舶尾轴为研究对象,建立尾轴-油膜-艉部结构系统动力学模型,研究发生冲击和碰摩之后的稳定性特征,为碰摩发生后轴系的安全评估提供一定的理论参考。
(1) 冲击和碰摩载荷都会对船舶推进轴系轴心运动产生扰动,从而影响其稳定性,影响程度与轴心转速有关。在轴心轨迹处于非周期运动区域内,载荷影响时间长,振幅衰减慢, 轴系恢复稳定状态的能力弱。
在周期运动区域,碰摩响应衰减快,而且轴的转速偏离该频率区域越远,碰摩响应振幅衰减越快,轴系恢复稳定状态的能力越强。
(2) 相对于冲击载荷,碰摩载荷发生后轴系恢复稳定所需的时间短。在碰摩载荷的作用下,一方面可通过调节轴系的工作速度能够回避碰摩作用对轴系的破坏作用;另一方面,发生碰摩时,合适的摩擦因数也会缩短尾轴的稳定时间,从而在一定程度上加强了船舶轴系保持稳定的能力。

