基于多传感器的AGV定位误差校正方法研究
曲立国, 邓亚颂
(安徽师范大学 物理与电子信息学院, 安徽 芜湖 241002)
0 引 言
自动导引运输车(Automated Guided Vehicle, AGV)是现代物流系统的重要组成部分, 随着物流行业的发展与科技技术水平的提升, 国内AGV技术发展迅速, AGV需求量居国际前列. AGV之所以能够实现无人驾驶, 导航和导引对其起到了关键的作用, 而AGV能否稳定精确地完成任务, 定位的准确性将会直接影响AGV导航的精度. 通常, 对于已知环境的定位方法主要分为相对定位法和绝对定位法. 相对定位法是指通常使用航位推算和惯性导航完成AGV姿态计算的导航方法, 但是这种方法的估计误差将会被累积. 随着导航技术的发展, 为了提高定位的准确性, 许多研究人员试图考虑将两种方法结合起来解决一些问题[1].
轮式AGV定位的最简单方法就是根据车轮的旋转角度得到AGV与道路的相对位置, 这一方法的弊病在于AGV在平坦的地面移动时, 轮子打滑是主要的方向误差来源. Cho B S等人利用惯性坐标系下线加速度传感器和角加速度传感器来进行导航位姿推算, 研究了接触面上的滑动误差的补偿等问题[2-5].
在近几年的研究中, 地标被广泛地应用于室内移动机器人定位, 地标被分为自然地标和人造地标, 人造地标相比于自然地标是它们不需要改变室内环境. Okuyama K等人将QR码作为人工地标引入到机器人的定位与导航上, 通过垂直于人工地标的摄像机检测到人工地标, 机器人读取QR码里设置的定位数据而得到确切位置, 进而校准机器人的姿态[6-8].
张涛等人将视觉信标和编码器数据进行融合来达到室内定位的目的, 使用Kalman滤波器融合编码器和视觉定位信息补充单个传感器定位的缺陷, 有效地提高了定位的精度[9-12].
基于QR码AGV定位系统如图 1 所示, QR码成网格状分布在操作空间中. 例如: 需要AGV从被标号为(0,0)的工作点行走至(2,2)的工作点, 在AGV的路径规划中选择(0,0)——(1,1)——(2,2)显然为最佳路径. 在此过程中需要AGV在(0,0)点首先要使小车方向调整为45°, 再从(0,0)——(1,1)——(2,2). 系统中有两个关键问题需要解决: 第一是AGV如何在QR码处确定前进的绝对角度, 保证正确到达下一个节点; 第二是离开QR码后, 在两个QR码之间如何进行局部的位置姿态调整, 保证行进方向的正确性, 以及如何补偿车轮打滑的问题.
针对此问题, 本文在分析已有研究成果的基础上, 重新设计编码器在AGV上的安装方法, 提出一种S形曲线修正算法, 解决两QR码间的AGV导航和车轮打滑问题. 其次, 实验中每经过一个QR码, 即通过QR码内嵌入标签号和位置信息, 相机在识别到QR码后, 提取QR码特征点在网络中的位置, 并且计算当前QR码与AGV之间的位置偏差和姿态, 根据QR码与AGV的位置关系对AGV的位置和姿态进行调整, 确定AGV的绝对行驶角度.

图 1 QR码分布图Fig.1 Distribution diagram of QR code
1 基于编码器的自定位校正系统
1.1 AGV的结构设计
AGV从结构上主要包含轮式、 足式、 履带式、 躯干式四个大类[13]. 本文AGV设计是为满足工业生产使用, , 四轮结构在稳定性方面要强于三轮结构, 所以采用四轮式AGV结构. 普通轮式AGV转向装置的结构一般分为两种方式: 一种是使用舵机转向, 前轮是自由轮, 后轮是驱动轮, 使用一个电机进行驱动, 转向使用舵机控制转向轮(前轮)实现; 另一种是采用差动控制转向, 与舵机转向相同的是, 后轮是驱动轮, 其左、 右轮使用独立的电机驱动, 前轮为自由轮, 转向通过控制左右驱动轮速度的方式实现[14].
综合考虑到AGV的稳定性以及对工作精确度的要求, 本文中AGV对以往的轮式AGV构造进行了改进, 采用了中间两轮做驱动轮, 且分别由两个直流电机进行控制, 前后各一个万向轮的结构布局, 使得小车可以前后左右自由地移动, 大大提高了AGV的可操作性、 稳定性以及转向精度.
其次, 轮式AGV在行走中容易出现车轮打滑的情况, 从而记录不了AGV行走的真实距离, 本文实验中AGV通过改装, 如图 2 所示, 形成一个与两边驱动轮同轴的编码器轮, 来测量AGV行走的真实距离, 为AGV的定位提供准确性. 与直流电机对应的的编码器通过改装, 与电机形成一个同轴线的转动效果, 车轮打滑时编码器轮却不打滑, 且与AGV之间通过减震弹簧连接, 从而不受AGV本身的压力影响, 使得在不影响AGV转弯的前提下达到精确测量AGV真实位移的效果. 此外相机安装在AGV驱动轮连轴的正中心, 因而角度上存在的误差不会被叠加到位置误差中, 进一步提高定位精度.

图 2 车体结构图Fig.2 Car structure diagram
1.2 S形曲线修正算法
针对以往研究中轮式AGV在行走的过程中容易出现车轮打滑, 从而偏离原路线行走, 使得无法测量真实位移的问题, 本文基于对AGV编码器的特殊设计提出了一种S形路径误差补偿的方法, 来修正由车轮打滑带来的误差, 使得车头保持直线向前行走.
如图 3 所示, AGV在行进过程中左右编码器记录的路程分别为SL1和SR1,θn为下一时刻AGV的航偏角与水平轴的夹角(θn为陀螺仪提供的相对角度), Δθn为AGV前后两个时刻位姿的变化量. 可分以下两种情况讨论:

图 3 AGV偏移示意图Fig.3 Diagram of AGV migration
1) AGV车轮不打滑时:SL1=SR1.
由于采样的周期性, 所以位置的推算为
(1)
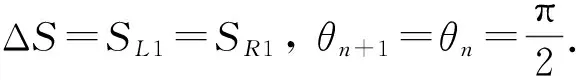
2) AGV车轮出现打滑时:SL1≠SR1.
若AGV发生偏移, 当SL1>SR1时, 如图 4 第一部分所示, 则
SL1-SR1=ΔS>0.(2)
根据图示几何关系, 为了保证AGV最后能回到原轨迹并且保持正方向不变, 直线向前行走, 按照本文提出的算法, AGV需要进行如图 4 第二部分所示的调整, 使左右两轮行进路程满足如下关系
SL2-SR2=-2ΔS.(3)

图 4 “S”形曲线修正路径图Fig.4 “S” curve correction path map
为了AGV最后能达到上述目的, 接下来还需要做如图 4 第三部分所示的调整, 使左右两轮行进路程满足如下关系
SL3-SR3=ΔS.(4)
根据以上算法推算在AGV发生偏移时, 进行以上两次算法调整则可以满足回到原轨迹并且保持正方向不变直线向前行走的目的, 若发生SL1 如图 3 中所示, 即为某一时刻车轮出现了打滑的情况, 则此时刻AGV的位置推算为 (5) 下面对如图4第二部分进行调整, 调整过程中位置推算公式为 (6) 为了保证AGV最后能回到原轨迹并且保持正方向不变直线向前行走, 接下来还需要做如图 4 第三部分调整, 调整过程中位置推算公式为 (7) 本实验模拟物流仓环境, QR码被粘贴在地板上, 以网格模式规则分布, 工业相机每次仅可以检测到一个QR码, 此设计的好处是每次相机确定的QR码位置为绝对位置. 如图 1 所示, QR码由草料二维码生成器软件生成. QR码的标签号和位置信息被编码在二维码中, 例如“(X,Y)=(00000001)”. QR码的方向如图 6 中YR方向, 固定为向上的方向为Y轴方向, 向右为X轴方向. 并且为了QR码被解码时, 它不会相互混乱, 生成的每个代码中的标签号和位置信息都各不相同. 在地图中每个点都为AGV的行进路线, AGV的每一次行走相当于从地图上一个坐标点移动到另外一个坐标点. 每一个QR码是AGV工作中使用的视觉信标节点, 如图 1 中将20个信标整齐地、 间距地、 同方向地排列在工作地面上, AGV通过安装于底部且垂直于地面的相机QR码进行识别. AGV的定位过程就是需要在每一个局部空间中实时反馈AGV的位置和航向角. 针对目前QR码在AGV应用上的问题, 本文利用局部QR码定位的准确性来进行AGV位姿的校正, AGV每次在QR码处确定前进的绝对角度, 保证正确到达下一个节点. 2.2.1 基于QR码的位姿推算 图 5 给出了AGV与QR码之间的位置关系, 其中Yw-Ow-Xw为世界坐标系下的位置坐标,Yc-Oc-Xc为AGV的坐标,Yr-Or-Xr为QR码坐标. (在本文实验中默认为QR码坐标与世界坐标重合, 忽略在粘贴QR码时的人为误差). 图 5 AGV与QR码之间的位置关系Fig.5 Position relation between AGV and QR code 如图 6 所示, AGV在工作中渐渐靠近QR码时, 相机能拍摄到图像信息, 相机的旋转中心还未与QR码的旋转中心重合, 而此时AGV的实时位姿推算可由以下算法求得: 设机器人坐标系下某二维码坐标为[xc,yc]T, 对应的世界坐标系下坐标为[xw,yw]T. 由公式推导可得 xw=xccosθα-ycsinθα+rx, yw=xcsinθα+yccosθα+ry.(8) 图 6 AGV渐近QR码时的位置关系Fig.6 The position relation of AGV asymptotically QR code 转换为矩阵形式有 Xw=H·Xc+r,(9) 其线性关系可表示为 Xw=[xw,yw,1]T,Xc=[xc,yc,1]T.(10) 结合式(1)~(3)可得 (11) 即线性关系式 Xw=Tw,c·Xc,(12) 式中:Tw,c为两坐标系之间相互变换的变换矩阵. 由式(5)也可写出其反向变换矩阵为 则可用T来表示AGV的位姿, 进行此次位姿的调整, 直到使AGV的旋转中心与QR码旋转中心重合, 结束此阶段局部的位姿校正. 2.2.2 基于QR码的偏转角校正 当AGV行进到QR码区域时, 会对相机中拍摄到的二维码进行解码, 提取QR码中编码的标签号和位置信息, 与地图上的信息进行比较确定AGV实时的位置坐标, 进行QR码局部的位姿校正, 是基于QR码与AGV之间旋转中心重合时的偏转角进行校正. 如图 7(a) 所示, 即为AGV旋转中心与QR码旋转中心重合时的一种情况, 在这种情况下需要基于QR码图像对小车的航偏角进行校正, 即对相机采集到的QR码图像进行处理. 为了更快和能够适应不同的光照强度, 首先对采集到的图像进行了灰度图像自适应阈值分割, 如图7(b)所示. 再对边缘进行直线提取求得二维码正向与AGV正向之间的偏向角, 如图7(c)所示. 在AGV旋转中心进行位置的校正是通过中间两个驱动轮差速控制来调整AGV的姿态. 图 7 QR码旋转中心信息的提取Fig.7 Extraction of information from the center of rotation of QR code 如图 8 所示为本次实验搭建的载体, 实验在2.4 m×1.6 m的地板上进行, 相机安装距离地面约为0.08 m, 地板上以0.8 m×0.8 m的地砖为基准等间隔铺设QR码, 目的是让AGV在此环境中按照命令进行自主行进. 图 8 实验载体AGVFig.8 Experimental carrier AGV 如图 9 为本文AGV定位轨迹结果, 图9中所示AGV行进轨迹设定为一个“C”字形, 和使用本文提出的S形曲线修正算法与QR码相结合的轨迹相比较, 只使用单个编码器轨迹存在误差累积问题. 而使用本文算法的轨迹始终在不停地调整, 在QR码处行进行进角度计算, 且在未检测到QR码时行走路径不停地逼近直线. 将本文定位轨迹与文献[15]的定位轨迹相比, 系统的航向误差不会出现如图 10 中航向角度误差随时间累积和转弯时定位出现偏差现象. 结果表明本算法可以用于室内AGV的路径控制中. 如图 11 所示为使用本文算法的AGV在X和Y轴方向上的位置偏差分布图, 由图可知当AGV上的视觉传感器采集到QR码时, 则利用第2节方法对AGV进行位置与姿态的校正. 当没有检测到QR码时, 则利用第1节方法对AGV位置进行估计并且利用S形曲线修正算法进行打滑误差的补偿, 从而达到降低定位、 导航误差的目的. 图 9 本文AGV定位轨迹图Fig.9 AGV location trace in this paper 图 10 文献[15]定位轨迹图Fig.10 Location trace in document [15] 图 11 X, Y轴方向位置偏差Fig.11 Position deviation of X, Y axis orientation 本文从AGV在应用中的两个关键问题入手, 介绍了一种基于编码器的S形路径修正算法, 并且设计了新的编码器安装方法, 使编码器轮与AGV车轮形成一个随动但相互不受力的效果. 其次将QR码应用到视觉定位中, 根据QR码与AGV的位置关系对AGV的位置和姿态进行调整以及进行角度的变换. 将QR码与编码器间隔使用, 补偿了编码器大角度范围变化下积累的误差. 实验结果表明此方法具有很好的实用性与稳定性, 定位精度也能够满足室内AGV的需求. 另外, 在实验中发现相机安装距地面的距离、 QR码大小和相机像素将会影响相机的识别精度, 值设置大于QR码宽度的一半可能会造成累计误差超过相机视觉范围偏离QR码, 造成误差的积累.
2 AGV位姿校正系统
2.1 QR码的分布及地图的创建
2.2 AGV位姿的校正


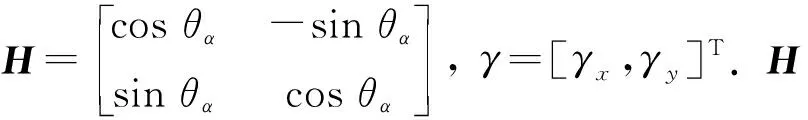
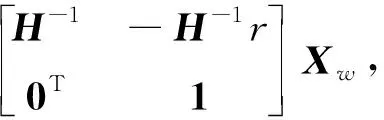

3 实验结果分析




4 结 论
——编码器

