一种改进的UKF-SLAM算法
吕太之, 周 武, 赵春霞
(1. 江苏海事学院 信息工程学院, 南京 210017; 2. 南京理工大学 计算机科学与技术学院, 南京 210094;3. 浙江师范大学工学院, 浙江 金华 321019)
0 引 言
自21世纪初以来, 国内外对机器人技术的发展越来越重视, 使其成为当今前沿高新技术研究最活跃的领域之一[1]. 同时定位与地图创建(simultaneous localization and mapping, SLAM)具有重要的理论和应用价值, 是实现移动机器人自主导航的关键. SLAM已经在移动机器人、 无人车辆、 无人水下航行器、 无人机、 增强现实等领域得到广泛应用[2-3]. 然而, SLAM技术仍然面临很多挑战, 如复杂的大环境、 可靠的数据融合、 非线性和未知的先验知识等[4-6].
SLAM问题的常用概率解决方案有两类, 基于卡尔曼滤波(Kalman Filter, KF)和基于粒子滤波(Particle Filter, PF)的SLAM算法[6]. 扩展卡尔曼滤波(Extended Kalman Filter, EKF)将非线性化的系统线性化, 来应用于SLAM问题的解决. EKF-SLAM在机器人导航领域被广泛应用, 相继在室内、 结构化道路、 水下等场合取得了成功. Bailey等人对EKF-SLAM算法进行了详细的论述和实验验证, 同时对EKF-SLAM算法进行了优化, 提高了状态向量维数很高时算法的效率[7]. 当路标数量较多时, EKF-SLAM计算量很大, 同时由于EKF在线性化的过程中, 不可避免的引入了线性化误差, 这样状态向量的估计就难以达到最优. 为了降低计算复杂度和减少线性化误差, 研究人员提出一系列改进方法. 降低计算复杂度的方法有不变扩展卡尔曼滤波(Invariant Extended Kalman Filter, IEKF)[8]、 平均扩展卡尔曼滤波(Mean Extended Kalman Filter, MEKF)[9]等. 对于提高算法精确度方面主要从运动模型的改进和减少由线性化带来的误差着手. 无迹卡尔曼滤波(Unscented Kalman Filter, UKF)使用UT(Unscented Transform)变换通过Sigma点重构出状态向量的统计特性(均值和误差), 为非线性化的SLAM问题提供了一种解决思路. Martinez-Cantin等[10]提出将UKF应用于机器人位姿和地图的估计. 曲丽萍[11]等提出基于平方根的无迹卡尔曼滤波, 在具有与UKF滤波相同精度的情况下, 确保了计算的稳定性和协方差矩阵的半正定性. 在UKF-SLAM的基础上, 学者们提出迭代平方根的UKF-SLAM[12]、 AUKF-SLAM(Augmented UKF-SLAM)[13]等算法.
除线性化误差和计算复杂度, 基于卡尔曼滤波的SLAM算法中一个不容忽视的问题就是外部干扰. 在真实环境中, 移动机器人轮胎打滑、 遇到障碍物导致前进受阻、 突发外力导致位置发生大的变化等外部干扰都会对SLAM产生较大的影响, 因此降低其鲁棒性, 甚至导致定位和地图创建的失败. 传统的卡尔曼滤波算法在受到外部干扰的情况下会导致误差急剧增加, 但随着不断的观测来更新状态, 误差会逐渐减少, 所以算法不需要考虑外部干扰的问题. 但卡尔曼滤波算法应用于SLAM问题上, 外部干扰在影响移动机器人定位的同时也会影响到环境地图. 环境地图和移动机器人定位相互影响, 不会随着观测来减少误差, 而是进一步累计误差. 传统UKF-SLAM算法并没有考虑外部干扰的影响, 因此, 当发生外部干扰情况的时候, UKF-SLAM算法会导致估计的不确定性远小于真实情况, 从而降低了SLAM的精度和鲁棒性. 为了减少外部干扰对SLAM算法的影响, 近几年各种不同的算法被提出. Ting[14]等通过对观测数据采用增量期望值最大的算法来检测外部干扰. Havangi[15]提出改进的模糊神经网络算法来动态调整先验知识的协方差. 然而该算法只调整观测误差的协方差矩阵R, 同时也容易受到累计误差的影响. Choi[16]等提出基于协方差膨胀的移动均值(Shifted Mean Based Covariance Inflation Technique, SMCI)方法来降低外部干扰的影响. SMCI-SLAM算法通过方差膨胀来减少外部干扰的影响, 但效果在下一个周期才能体现, 同时没有区别对待不同类型的外部干扰, 也容易受累计误差的影响.
基于前期研究成果[17], 针对外部干扰会导致基于UKF-SLAM算法精度降低甚至发散的问题, 提出了一种改进的UKF-SLAM算法. 算法主要特点在于:
1) 继承抗外部干扰的EKF-SLAM算法, 将其应用于UKF-SLAM算法, 通过临近观测分析来检测外部干扰, 不会受累计误差的影响, 提高了外部干扰检测的精度.
2)不仅处理干扰对控制输入的影响, 也处理干扰对观测过程的影响. 将干扰分类处理, 根据不同类型的外部干扰使用不同方式来膨胀系统状态方差, 扩大其不确定性, 使系统状态迅速收敛到真值.
3)改进干扰检测算法, 根据临近观测对比以及控制噪声和观测噪声协方差矩阵来判断是否发生小概率事件, 以此确定SLAM过程是否存在外部干扰.
1 SLAM问题描述
SLAM问题可以描述为机器人在未知环境中从一个未知的位置开始移动, 在不断的移动中根据控制信息和传感器观测进行自身定位, 同时构建增量式地图. SLAM的主要目标就是基于一组从开始到t时刻带有误差的控制数据u1:t和观测数据z1:t中获得对移动机器人位姿和地图信息最好的估计. SLAM问题可以描述为如下的后验概率.
p(xi,Θ|z1:t,u1:t),(1)
式中:xt是当前机器人的位姿;Θ是环境地图.xt可以通过上一时刻位姿xt-1和当前时刻控制数据ut的概率函数来表示, 称之为运动模型.
xt=g(xt-1,ut)+εt,(2)
式中:εt为服从高斯分布的运动模型噪声. 通过传感器获得的观测数据同样可以被概率函数表示, 称之为观测模型.
zt=h(xt,Θ)+δt,(3)
式中:δt为服从高斯分布的观测模型噪声.
基于运动和观测模型, SLAM问题的后验概率可以使用贝叶斯滤波器迭代更新, 式(1)改写成
p(xt,Θ|z1:t,u1:t)=ηp(zt|xt,Θ,z1:t,u1:t),
p(xt,Θ|z1:t-1,u1:t,x0).(4)
卡尔曼滤波和粒子滤波都是典型的贝叶斯滤波. 卡尔曼滤波是将SLAM后验概率描述为均值为xt, 协方差为Pt的多维高斯分布. 粒子滤波则是用有限的样本集合来代表SLAM的后验分布.
2 UKF-SLAM算法
EKF在迭代更新移动机器人状态时采用泰勒级数线性化系统模型, 不可避免地引入了线性化模型误差, 同时雅可比矩阵的更新也增大了EKF的计算量. 无迹卡尔曼滤波(Unscented Kalman Filter, UKF)是用2L+1(L为系统状态的维数)个能表征系统状态向量的Sigma点重构出系统统计特性. 通过非线性系统模型来实现机器人系统状态的更新, 提高了估计的精度, 同时该算法不需要推导系统的雅可比矩阵, 节省了计算时间. 基于此, UKF被广泛应用于SLAM问题中[10, 18].
UKF-SLAM初始化过程包括均值、 协方差矩阵和Sigma点权值的设置.
x0=xinitP0=Pinit,(5)

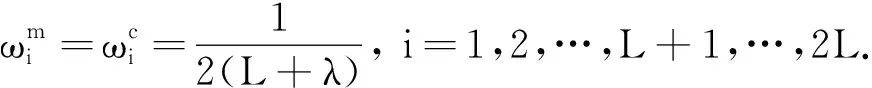
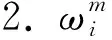
通过Sigma点计算、 预测和观测更新三个步骤完成状态向量和协方差矩阵的迭代更新.
1) Sigma点计算
若t-1时刻系统状态均值和协方差为xt-1和Pt-1, 首先增广系统状态向量得到如下均值和方差.
(8)

式中:Q和R分别代表控制噪声和观测噪声的协方差矩阵. 根据增广矩阵计算Sigma点.
(10)
尺度常量η计算如下
(11)
2) 预测
根据上一时刻的Sigma点和运动模型预测t时刻的Sigma点.
(12)
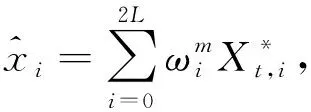
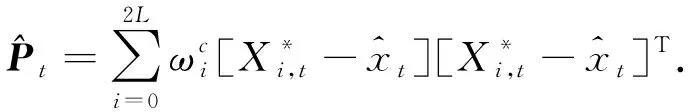
3) 更新
(15)


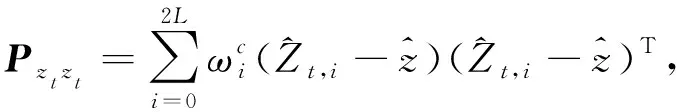
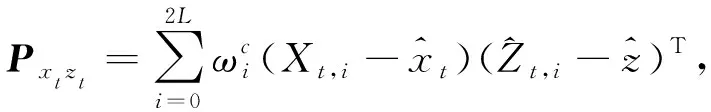
Kt=Pxtxt(Pxtzt)-1,(20)
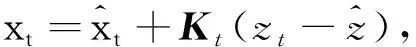
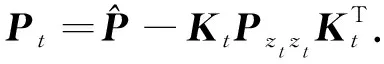
3 改进的UFK-SLAM算法
3.1 算法设计思路
在未知环境中探索的时候, 外部干扰会导致误差突然增大, 从而降低SLAM估计精度和鲁棒性. 在SLAM过程中, 移动机器人会根据上一时刻的状态和控制输入来预测当前位姿和路标位置. 如果观测传感器观测的数据与预测的数据一致, 系统状态的更新是可靠的; 反之则是不可靠的, 有很大可能性发生了外部干扰. 外部干扰主要分为以下两类情况:
一类是移动机器人自身受到外部干扰, 导致此类情况的主要原因有: ① 外力的作用而导致移动机器人位姿发生较大的改变; ② 移动机器人遇到障碍物或者地面潮湿等原因而导致车轮打滑使得从里程计读取的数据不能真实反映其运动状态; ③ 惯性测量单元发送故障, 读取的是错误数据.
另一类情况是路标受到外部干扰, 导致此类情况的主要原因有: ① 由于外力的作用导致路标的自身位置发生了改变; ② 观测传感器发生故障, 读取的是错误数据.
针对外部干扰影响SLAM估计精度问题, 本文提出一种改进的UKF-SLAM算法. 本文算法在UKF-SLAM算法基础上增加干扰检测和系统状态方差膨胀的过程. 临近观测的不一致性能判断出预测和观测数据是否一致, 被用于外部干扰的检测. 当检测到存在外部干扰的时候, 针对不同类型的外部干扰, 通过膨胀系统状态协方差矩阵, 扩大其不确定性, 使系统状态迅速收敛到真值, 提高算法的估计精度和鲁棒性.
3.2 干扰检测和状态方差膨胀
提出算法通过对比t-1时刻和t时刻的观测来检测移动机器人是否受到外部干扰. 假定t-1时刻移动机器人处于原点位置, 前进的方向为X轴.t-1时刻机器人观测到的第j个路标信息为zt-1(mj)= [lt-1(mj),βt-1(mj)]. 以t-1时刻移动机器人位置为原点, 第j个坐标的位置为
(23)

(24)
式中: ΔT为采样周期;vt为车辆后轴中心处运动速度;αt为车辆的转向角;L为两轴的轴距. 通过平移和旋转操作, 可以获得第j个路标以t时刻机器人为原点下的预测位置
(25)

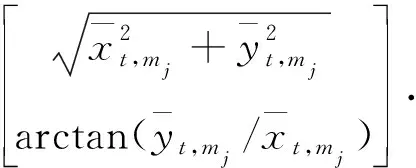
最后通过临近两次观测不一致性来确定移动机器人或者路标是否受到外部干扰.
1) 移动机器人受到外部干扰
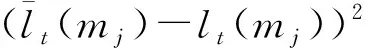
(27)
式中:Sm是观测函数关于路标位置的雅可比矩阵.Dlt(mj)~N(0,1)服从正态分布. 当该值大于2.3即小概率事件发生的时候, 表示由于外部干扰的影响导致对路标的观测存在较大误差的可能性较大. 根据观测路标数量、 控制和观测误差协方差矩阵设定阀值, 当存在较大观测误差的路标数量超过阀值, 就认定移动机器人受到外部干扰.

(28)
Dβt(mj)~N(0,1)服从正态分布. 当对多个路标观测Dβt(mj)超过指定阀值并且角度偏移方向趋于一致的时候就认定移动机器人受到外部干扰.
当判断移动机器人受到外部干扰的时候, 下一步的工作就是修复此类干扰. 本文算法对移动机器人位姿状态的协方差矩阵进行膨胀, 以此来加大机器人的不确定性, 让系统状态更倾向于观测的结果, 从而在更新过程中使机器人更接近于真实的位置.

式中: avg(diffl)和avg(diffβ)代表路标预测值和观测值在距离和角度上的平均偏差值;Gut是运动模型关于控制输入的雅可比矩阵.
2) 路标受到外部干扰
当只有单一路标预测值与观测值之间的距离差值超过阀值, 就认定该路标由于受到外部干扰而导致位置发生了改变. 假定第j个路标受到外部干扰, 通过对该路标的协方差矩阵Pm,j进行膨胀,以此来加大该路标估计的不确定性, 让系统状态更倾向于移动机器人的位姿和其他路标观测的结果, 从而使得对系统状态的更新更接近于真实值.

式中:diffl,j和diffβ,j代表第j个路标预测值和观测值在距离和角度上的偏差;Ht是观测模型关于状态向量的雅可比矩阵.
3.3 算法流程
本文算法改进UKF-SLAM, 增加了干扰检测的过程, 当检测到系统中存在外部干扰时, 通过对系统状态方差的膨胀, 加大移动机器人或路标估计的不确定性, 提高了SLAM估计的精度. 算法1描述t时刻干扰检测和状态方差膨胀的流程.
算法1 干扰检测和状态方差膨胀
输入:
t-1时刻协方差矩阵Pt-1,t-1时刻观测zt-1,t时刻观测zt
步骤:
∥如果临近观测相同路标数量小于3, 不进行外部干扰检测
if (sameObservedLandmark(zt-1,zt)<3)
return;
end if
∥根据临近两次观测检测是否存在外部干扰
disturanceType=checkDisturance(zt-1,zt);
if disturanceType==ROBOTDISTURANCE
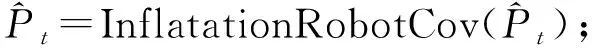
else if disturanceType==LANDMARKDISTRUANCE
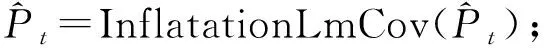
end if
输出:
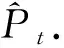
本文算法在UFK-SLAM数据关联和系统状态更新流程之间增加了干扰检测和状态方差膨胀的过程. 由于是在系统状态更新之前引入外部干扰检测和状态方差膨胀, 所以本文算法能在干扰发生的周期内做出快速响应. 图 1 描述了t时刻改进UKF-SLAM算法更新系统状态的流程.

图 1 改进UKF-SLAM算法流程图Fig.1 The flowchart of the improved UKF-SLAM algorithm
4 仿真实验结果及分析
为了测试算法性能, 设计了UKF-SLAM[10]、 SMCI-SLAM[16]和改进UKF-SLAM算法的仿真对比实验. 移动机器人t时刻的运动和观测模型采用式(31)和(32). 给定控制输入ut=[vt,αt],vt是车辆后轴中心处运动速度,αt是车辆的转向角. 移动机器人运动模型可表示为

式中: ΔT为采样周期;ε为控制噪声;L为两轴的轴距. SLAM问题假定控制噪声服从高斯分布.
观测数据由路标的距离lt(mj)和方向角βt(mj)组成.t时刻移动机器人观测方程为
(32)


4.1 移动机器人受到外部干扰
设计一个大小为250 m×200 m的包含75个路标的仿真环境, 如图 2(a)所示, 移动机器人的初始位置为(0,0).
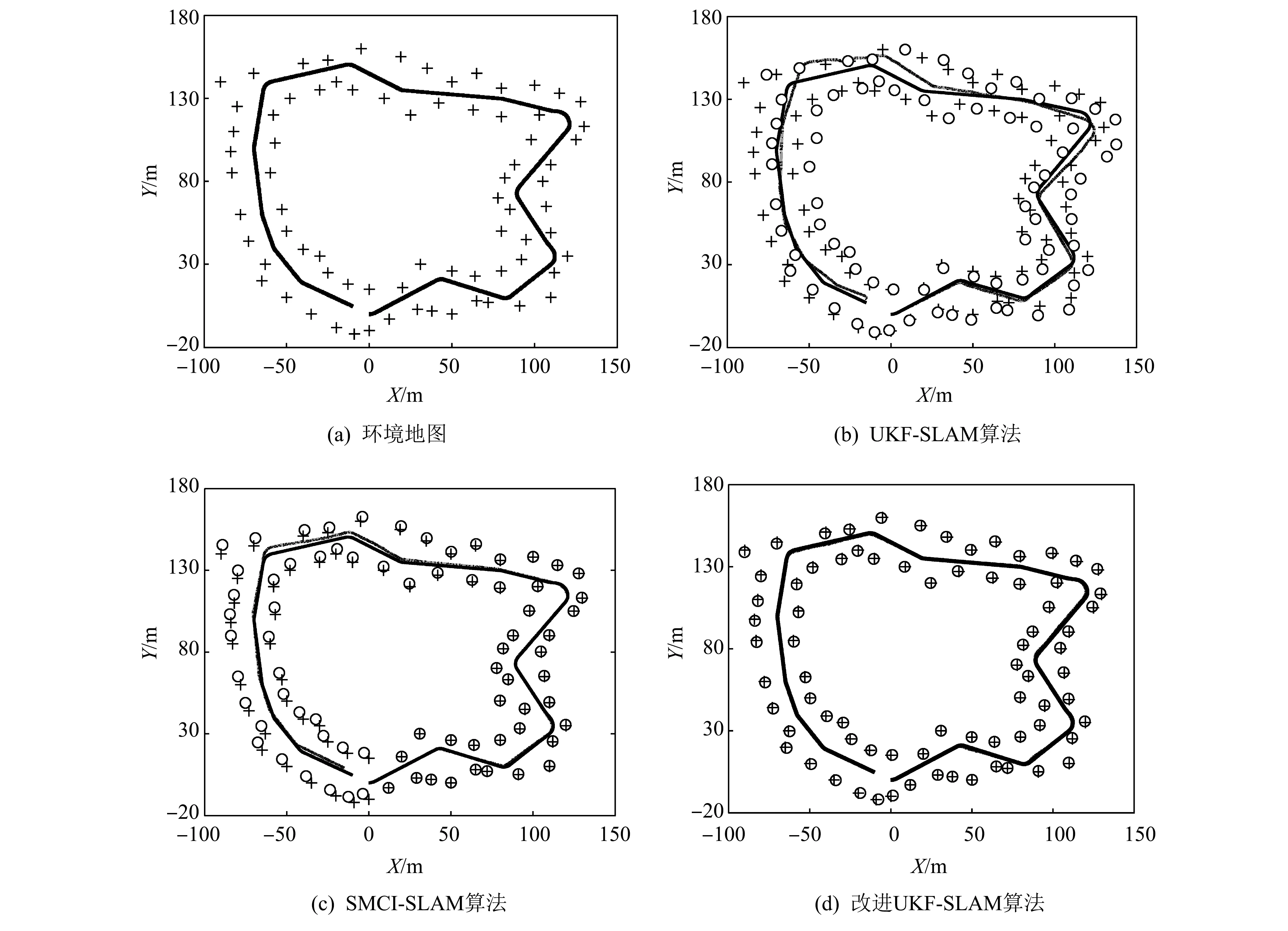
图 2 三种算法在机器人受到外部干扰下的实验结果Fig.2 Comparison between the three algorithms with outlier disturbances on robots
移动机器人在此环境运动过程中, 每100个控制周期会随机产生3~5次外部干扰. 由于外部干扰的存在导致移动机器人实际的位姿改变与控制输入相差甚远, 从而影响机器人定位和地图创建的精度. 在此环境中采用UKF-SLAM、 SMCI-SLAM和改进UKF-SLAM算法对移动机器人的路径和环境中的路标进行估计, 三种算法均假定数据关联已知. 仿真实验结果如图2(b)~图2(d), 图中实线表示移动机器人的运行轨迹, 虚线表示各个算法预估的路径. 加号表示路标的真实位置, 圆圈表示各个算法估计的路标位置.
从图 2 中可以看出, 虽然三种算法与机器人真实的路径都存在一定的误差, 但是改进UKF-SLAM算法无论在机器人路径估计还是路标位置估计上的误差都要小于UKF-SLAM和SMCI-SLAM算法, 即改进UKF-SLAM算法的估计更接近真实的状态.
由于在仿真环境中, 运动和观测噪声是随机的, 每次实验的结果都是不一样的, 所以不能仅用某一次的实验结果来判断算法的性能. 均方根误差(root-mean squared error, RMSE)用来衡量观测值和真实值之间的偏差, 能很好地反映出算法的精确度. 以RMSE为标准, 对UKF-SLAM、 SMCI-SLAM和改进UKF-SLAM算法进行比较. 使用图2(a)所示仿真环境, 在机器人运动过程中, 随机产生外部干扰. 为了更详细地评估三种算法的性能, 实验执行了50次, 结果如表 1 所示. RMSE_P表示机器人位置估计的均方根误差, RMSE_L表示路标位置估计的均方根误差.

表 1 三种算法的50次仿真实验对比
改进UKF-SLAM算法比UKF-SLAM在移动机器人位置和路标估计上的RMSE分别降低了53.80%和57.16%, 比SMCI-SLAM算法在移动机器人位置和路标位置估计的RMSE分别下降了31%和35%. 实验证明, 在移动机器人受到外部干扰的环境中, 通过干扰检测和状态方差膨胀可以改进SLAM估计的精度. 由于干扰检测只对比了相邻两次观测的路标, 所耗费的时间有限, 故改进UKF-SLAM算法与UKF-SLAM和SMCI-SLAM算法执行时间上接近.
在50次仿真实验中, 移动机器人每次运动大约190 s. 图 3 所示为UKF-SLAM、 SMCI-SLAM和改进UKF-SLAM算法基于时间的移动机器人位姿估计均方根误差曲线图. 图中包含了四幅子图, 分别是基于X轴、Y轴、 方向角和位置的均方根误差. 从图3中可以看出, 改进UKF-SLAM比其他两种算法在整个实验过程中都更接近移动机器人的真实位置, 证明干扰检测和状态方差膨胀可以有效提高移动机器人位姿估计精度.
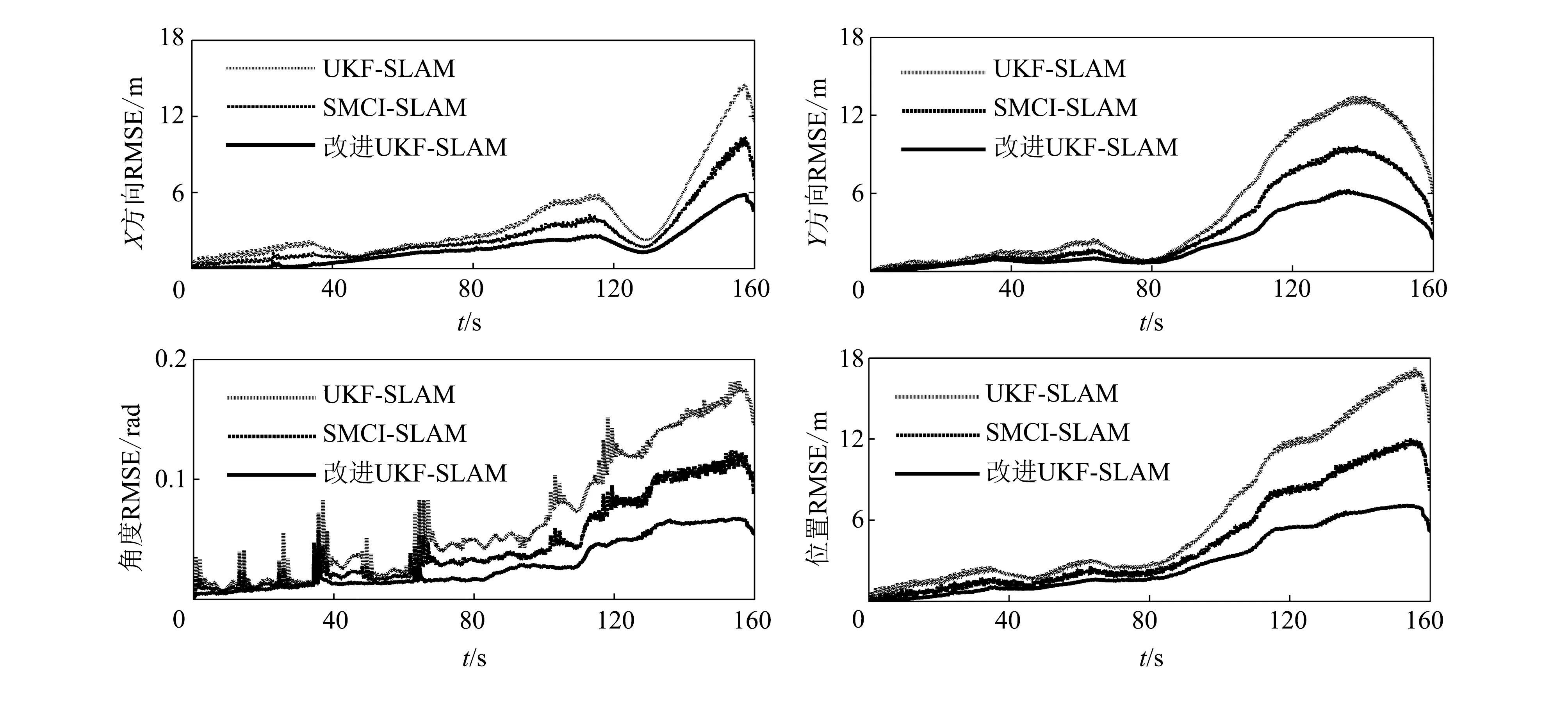
图 3 三种算法在机器人位姿上的均方根误差Fig.3 The RMSE comparison in position among the three algorithms
图 4 所示为路标位置的均方根误差曲线图. 从图中可以看出, 改进UKF-SLAM算法比其他两种算法对于路标位置的估计误差要小.

图 4 三种算法在路标位置上的均方根误差Fig.4 The RMSE comparison in landmark position between the three algorithms
4.2 路标受到外部干扰
采用与前面实验相同的仿真环境, 在机器人移动过程中坐标为(12,-3), (125,105)和(-20,140)的3个路标由于受到外部干扰的影响, 位置发生了改变. 在路标受到外部干扰的环境下使用UKF-SLAM、 SMCI-SLAM和改进UKF-SLAM算法对移动机器人的路径和环境中的路标进行估计. 三种算法均假定数据关联已知, 仿真实验结果如图 5(b)~图5(d)所示.
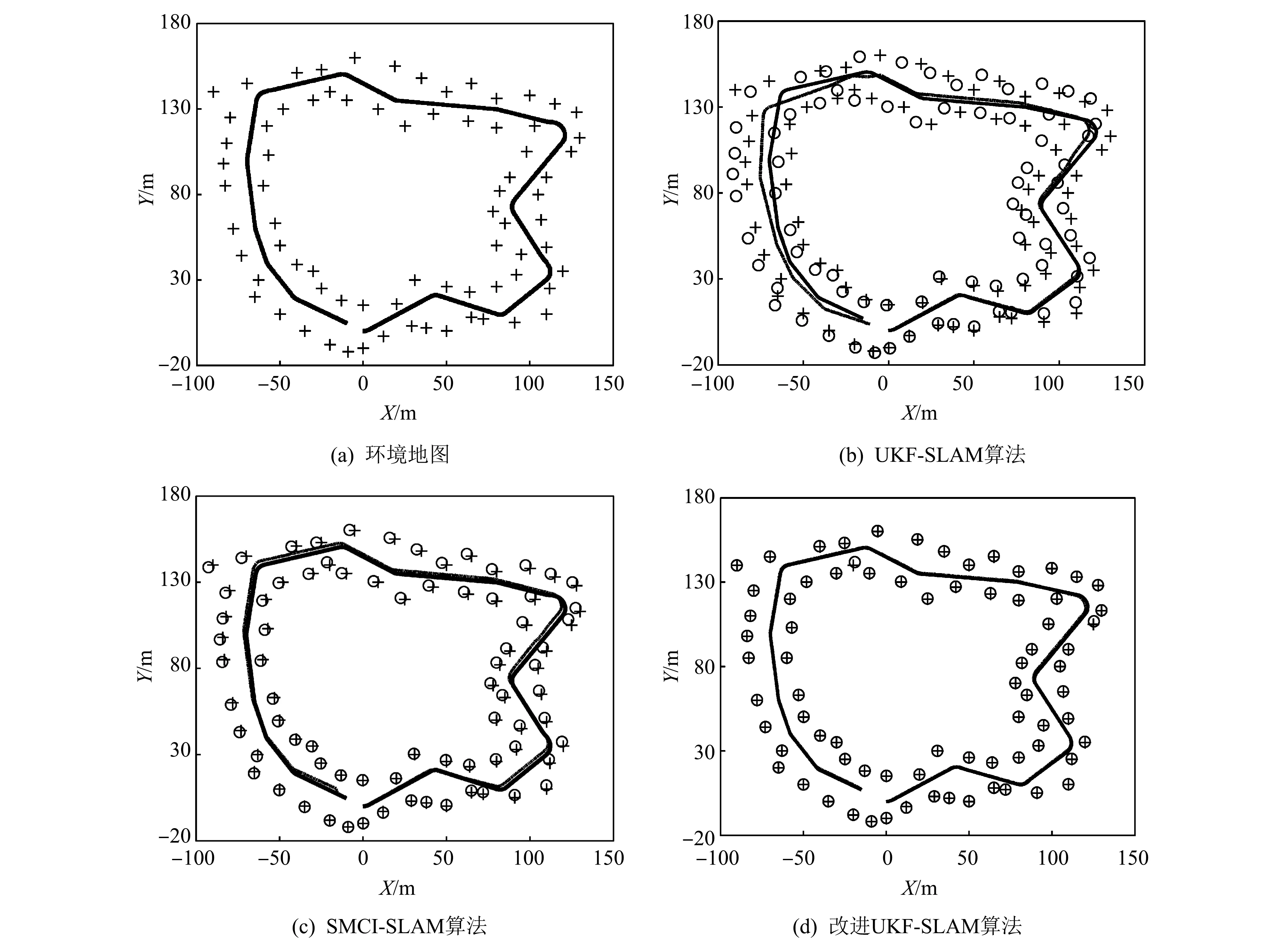
图 5 三种算法在路标受到外部干扰下的实验结果Fig.5 Comparison between the three algorithms with outlier disturbances on landmarks
在UKF-SLAM算法中, 某个路标位置的改变不仅影响地图估计, 也影响了移动机器人定位的精度. 由于采用固定的噪声模型, 使得对位置已改变路标的过分信任, 导致移动机器人位姿和其他路标位置向已改变位置路标偏移. 在UKF-SLAM算法中误差是累计的, 最终会使得无论在地图估计上的误差还是机器人定位估计上的误差都会变大. SMCI-SLAM算法和改进UKF-SLAM算法通过对系统状态的膨胀降低了对位置改变路标的信任, 提高了SLAM的估计精度. 通过系统状态膨胀, 虽然可能会降低被改变路标位置估计的精度, 如图5(d)改进UKF-SLAM算法对于坐标为(12,-3)的路标估计精度不如UKF-SLAM, 但是如果不膨胀系统状态, 会导致移动机器人定位和地图中其他路标位置估计精度的降低, 如图5(b)中, 由于该路标位置的改变, 导致移动机器人的位置和其他路标位置都发生了偏移, 由于误差是累计的, 从而导致后面对系统状态估计的误差越来越大. SMCI-SLAM算法是在路标受到外部干扰影响的下一个周期才使用膨胀后的协方差更新地图和机器人位置, 同时也受累计误差的影响. 改进UKF-SLAM算法在路标受到外部影响的周期内就使用膨胀后的协方差更新系统状态, 能够快速地对外部干扰做出反应, 同时不受累计误差的影响, 也对外部干扰做出了分类, 所以更能反映真实的环境. 从图中也可以看出, 改进UKF-SLAM估计的精度要优于SMCI-SLAM和UKF-SLAM算法.
由于运动和观测噪声的随机性导致每次实验的结果不一样, 这里仍然以RMSE为标准, 对UKF-SLAM、 SMCI-SLAM和改进UKF-SLAM算法进行比较. 环境地图使用图5(a)的仿真环境, 在移动机器人运动过程中, 会随机产生外部干扰导致3~5个路标位置发生改变. 实验执行了50次, 结果如表 2 所示, 结果表明在路标受到外部干扰的环境中, 通过干扰检测和状态方差膨胀可以改进SLAM估计的精度.

表 2 三种算法的50次仿真实验对比
5 结束语
对外部干扰影响SLAM估计精度的问题, 提出了改进的UKF-SLAM算法. 所提算法在系统状态更新之前引入外部干扰检测和状态方差膨胀, 能在干扰发生的周期内快速做出响应. 临近观测的不一致性用于检测外部干扰不受累计误差的影响, 提高了检测的精度. 外部干扰分为移动机器人受到的外部干扰和路标受到的外部干扰, 对它们使用不同方式膨胀系统状态协方差可以获取更精确的系统状态估计. 仿真实验结果表明, 改进UKF-SLAM算法比UKF-SLAM和SMCI-SLAM算法在系统发生外部干扰的情况下对系统状态的估计更加精确, 同时增加的系统开销也很小.

