基于后悔理论和证据推理的风险型多属性决策

吴 扬， 郭 敏， 李彦华

(中北大学 经济与管理学院， 山西 太原 030051)

0 引 言

风险型多属性决策是指在不确定自然状态下， 考虑多个属性或指标， 对有限方案进行排序. 其特点是在决策过程中存在两个及以上的自然状态， 且无法确定未来会出现哪种状态[1]. 对于风险型多属性决策问题的研究具有广泛的实际背景， 然而现实中由于决策问题客观的复杂性、 不确定性等以及决策者的行为受心理活动的影响等， 多属性决策往往存在以下问题： 1) 决策信息不确定、 不完全， 难以用精确值描述. 2) 如何集结不确定信息， 得到更可靠的评价结果. 3) 选择什么样的分析方法， 来反映决策者的行为.

对于问题1),可以采用区间数、 模糊数、 语言值等形式来表示不确定信息. 其中， 区间数能够简洁有效地表示不确定信息， 在多属性决策问题中得到了广泛应用. 如张自欣[2]利用区间数表示某时间段内系统各指标的动态变化， 解决了突发事件的动态预警问题. 李磊[3]等使用区间数来体现群决策的综合意愿， 提出一种基于区间数的组合算法来进行方案排序. 对于决策信息的不完全性， 研究者通常只假设属性权重信息不完全或只假设自然状态发生概率信息不完全， 很少有研究将这两类不完全信息同时考虑. 显然， 对属性权重信息和自然状态发生概率信息都不完全情况下的多属性决策问题的研究更具有现实意义和研究价值.

对于问题2)， Yang[4]等提出的证据推理法在不确定多源信息融合方面具有优势. 近年来已成为研究热点. 如包甜甜[5]等针对不确定的混合多属性决策问题， 提出基于前景理论和证据推理的直觉模糊决策方法. 何小雨[6]等结合证据推理法解决了群层次分析法在不确定信息处理方面的缺陷. Wang[7]等针对模糊多属性决策问题， 提出了基于直觉模糊集和证据理论的决策方法. 对于区间型属性值， 运用证据推理法不需像文献[1]中以某种分布将其转化为实数， 能够减少类型转换造成的信息丢失.

对于问题3)， 通常有两类分析方法来反映决策者的行为. 一类是基于期望效用理论， 假设决策者的行为是完全理性的. 另一类是基于前景理论或后悔理论等， 假设决策者是有限理性的. 较之前一类， 有限理性分析方法更能反映现实中决策者的决策行为， 已成为研究主流. 后悔理论虽较前景理论简单但同样能够解释所有违背期望效用理论的现象[8]， 因而越来越引起学者们的关注. 如朱轮[9]等利用后悔理论构造出决策者对各属性的感知效用值， 从而构建了最优化模型. 张晓[10]等针对属性值和自然状态发生概率均为区间数的情况下， 利用后悔理论来构建决策者对各属性的感知效用值， 提出了基于后悔理论的风险型多属性决策方法. 钱丽丽[11]等针对灰色随机多准则决策问题,在考虑决策者的风险态度及心理行为的情境下， 提出了一种基于后悔理论的决策方法. 相比于前景理论， 后悔理论还考虑到了备选方案对决策者所选方案的影响， 对于方案选优问题具有一定的参考价值.

本文针对属性值为区间数、 各属性权重及各自然状态发生概率信息均不完全的风险型多属性决策问题， 提出一种基于后悔理论和证据推理的风险型多属性决策方法. 该方法通过两阶段证据融合得到各方案的综合感知效用值， 在此基础上， 通过构建方案综合感知效用最大化的优化模型， 得到各属性权重和各自然状态发生概率. 最后根据各方案的综合感知效用两两比较可能度矩阵进行排序.

1 基本知识

1.1 后悔理论

后悔理论由Bell、 Loomes和Sugden分别提出， 它将决策者的后悔和欣喜两种心理纳入到决策过程中. 根据该理论， 决策者对方案的感知效用由效用函数v(x)和后悔-欣喜函数R(Δv)组成. 当R(Δv)>0时， 表示欣喜值； 当R(Δv)≤0时， 表示后悔值. 后悔或欣喜值是通过所选方案与备选方案比较得到的. 假设有两个方案A和B， 对应的决策信息为x和y， 那么决策者对方案A的感知效用值为

U(x)=v(x)+R(Δv),(1)

式中： Δv=v(x)-v(y),v(x)和v(y)表示决策者对方案A和B的决策信息x和y的感知效用.

1.2 证据推理

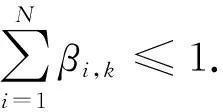
(2)

其中，

wk表示第k个属性的权重.

1.3 区间数运算及排序

定义1 记a=[al,au]为一个区间数， 满足al≤au. 当al=au时，a退化为一个实数. 定义运算法则如下： 设a=[al,au]，b=[bl,bu]， 则：

1) 当al=bl且au=bu时，a=b.

2)a+b=[al+bl,au+bu].

定义2 对于区间数a=[al,au]和b=[bl,bu]， 令d(a,b)表示区间数a和b的距离， 则[13]

(3)

定义3 对于区间数a=[al,au]和b=[bl,bu]， 令La=au-al，Lb=bu-bl，p(a≥b)为a≥b的可能度.

1) 当La和Lb中至少有一个不等于0时，p(a≥b)的计算公式为[14]

(4)

2) 当La=0且Lb=0时，a,b均为实数.p(a≥b)的计算公式为

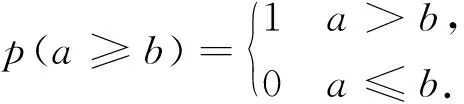
(5)

2 风险型多属性决策模型

2.1 问题描述

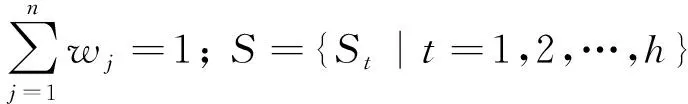
本文假设权重信息和自然状态信息是不完全的. 令W∈δ1， 其中δ1表示属性权重的不完全信息数学表达式的集合， 具体可分为以下5种情形[15]：

1)wk1-wk2=εk1;

2)wk1≥σk1wk2;

5)wk1-wk2≥wk3-wk4,k1≠k2≠k3≠k4.

2.2 感知效用值的计算

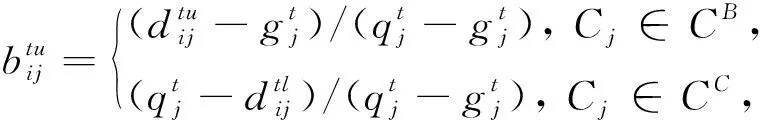
其中，

v(x)=xα,(7)

式中：α表示风险规避系数. 0<α<1， 且α越小风险规避程度越大.

然后， 计算每个方案的各属性相对于其他方案各属性的后悔-欣喜值. 现实中决策者会尽量地减少后悔， 所以假设决策者是后悔规避的. 因而，R(v(xi)-v(xk))是单调递增的凹函数, 满足R′(v(xi)-v(xk))>0，R″(v(xi)-v(xk))<0.R(v(xi)-v(xk))可以表示为[10]

R(v(xi)-v(xk))=1-e-δ(v(xi)-v(xk)),(8)

式中：δ表示后悔规避系数，δ>0.δ越大后悔规避程度越大.

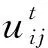
(9)

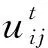
2.3 感知效用值的融合

(10)

其中，

其次， 设H={H1,H2}为识别框架, 其中H1代表“感知效用值的肯定程度”；H2代表“感知效用值的否定程度”；H代表“感知效用值的未知程度”. 用βtk,i(j)表示状态Si下， 方案Ai的属性Cj属于Hk的置信度， 其中k∈{1,2}. 则

(11)

然后， 以状态Si下方案Ai的所有属性的等级评价结果为证据， 依据式(2)进行证据融合， 得到状态St下方案Ai被评价为等级Hk的置信度

t∈H,i∈M,k∈{1,2},(12)

其中，

i∈M,k∈{1,2},(13)

其中，

那么， 决策者对方案总的等级评价结果为

S(Ai)={(Hk,βk,i(W,P)),k=1,2},i∈M.

方案Ai的综合感知效用为

其中，

(14)

2.4 决策优化模型的构建

对于模型(15)， 若最优解不存在， 那么需要对属性权重信息或自然状态概率信息进行调整. 若存在多个最优解， 那么需要进行灵敏度分析， 并在此基础上选择符合决策者偏好的解.

2.5 灵敏度分析

2.6 方案排序

1) 当Li和Lj至少有一个不为0时，Ei,j的计算公式为

i,j∈M,i≠j.(16)

2) 当Li=0且Lj=0时，Ei,j的计算公式为

(17)

根据式(16)和(17)建立各方案的综合感知效用值两两比较可能度矩阵

E=[Ei,j]m×m=

利用文献[14]中给出的排序公式

(18)

得到可能度矩阵E对应的排序向量π=(π1,π2,…,πm)T， 并根据πi(i∈M)对各方案进行排序.

综上所述， 基于后悔理论和证据推理的多属性决策方法的步骤如下：

步骤 1： 根据式(6)将原始决策矩阵D转化为规范化决策矩阵B.

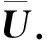
步骤 5: 将各方案的综合等级评价结果S(Ai)转化为综合感知效用值ui(W,P)， 如式(14)所示.

步骤 6: 建立如式(15)所示的最优化模型， 并运用Matlab编程求解. 获得各方案的感知效用值ui(W,P).

步骤 7: 根据式(16)～(17)建立各方案的综合感知效用值两两比较可能度矩阵E， 并根据式(18)进行排序.

3 算 例

下面采用文献[13]中的算例和数据来验证本文方法的有效性. 某电子产品生产企业考虑开发一种新电子产品并投放到市场. 现有5个方案(A1,A2,…,A5)可供选择. 需要考虑属性：C1: 市场需求(单位： 万台/年)，C2: 收益率(单位： %/年)，C3: 投资回收期(单位： 年). 其中C1和C2为效益型属性，C3为成本型属性. 在产品市场投放期间， 有3种可能的自然状态：S1: 好，S2: 中，S3: 差. 已知各属性权重δ1∶w1=0.35,w2=0.4,w3=0.25; 自然状态概率信息δ2∶0.3≤p1≤0.5, 0.4≤p2≤0.6, 0.1≤p3≤0.3.

根据式(6),将文献[13]案例中的数据进行归一化处理.

参考文献[16]中经过实验验证的数据, 令α=0.88,δ=0.3， 根据式(7)～(9)计算感知效用值， 并根据式(10)对感知效用值进行规范化， 结果如表 1 所示.

表 1 决策者感知效用值矩阵

根据式(16)～(17)建立各方案的综合感知效用值两两比较可能度矩阵:

根据式(18)得到可能度矩阵E的排序向量：π=[0.137,0.252,0.130,0.108,0.248]. 所以方案的排序结果为：A2>A5>A1>A3>A4.

使用文献[10]提出的基于后悔理论的风险型多属性决策方法和文献[13]提出的基于前景理论的风险型多属性决策方法分别求解该问题， 得到的排序结果与本文方法所得的排序结果比较如表 2 所示.

表 2 排序结果比较

比较上述3种方法可以看出， 使用本文所提出的方法来解决上述问题， 得到的排序结果与文献[13]中基于前景理论的排序结果基本一致， 且最优方案都为A2. 但相比于文献[13]基于前景理论的多属性决策方法， 本文提出的方法不需另外设置参考点， 且使用了更少的参数， 可操作性强. 利用文献[10]所提的方法来解决上述问题， 得到的方案排序与本文所提方法完全一致， 但是文献[10]以某种假定的分布将具有不确定性的区间属性值转化为确定性的实数型属性值， 可能会造成信息的丢失. 而本文利用证据推理法避免了将区间性属性值转化为实数型属性值， 保留了属性取值的不确定性.

为进一步说明本文方法的有效性， 将上述问题中的自然状态概率向量确定为P*=(0.3,0.4,0.3)， 使用区间加权平均算子(IVWA)对表 1 中的属性值进行集结， 得到各方的综合感知效用值为u1=[0.130,0.554],u2=[0.574,0.970],u3=[0.075,0.596],u4=[0.095,0.466],u5=[0.595,0.969]. 与本文使用证据推理法得到的结果对比， 如图 1 所示.

可以看出本文使用证据推理法进行不确定信息集结， 在保留不确定性的同时具有更高的精度.

图 1 两种方法决策结果对比图Fig.1 Comparison of the result of two methods

此外， 本文提出的方法可以处理属性权重的信息和自然状态发生概率的信息都不完全的情况， 使其具备更广泛的适用范围. 下面在各属性权重信息和各自然状态发生概率信息都不完全情况下， 来验证本文所提的方法. 首先， 将上述问题中的属性权重也改为不完全信息表示. 即， 假定为δ1：0.1≤w2-w1≤0.2， 0.4≤w2≤0.6, 0.6w1≤w3≤0.9w1, 其他条件不变. 然后， 仍可建立式(15)所示的模型. 最后， 求解得到最优属性权重向量W*=(0.31,0.41,0.28)和最优点概率向量P*=(0.3,0.4,0.3). 基于可能度矩阵的排序向量为：π=[0.138,0.251,0.129,0.108,0.249]， 所以方案的排序结果为：A2>A5>A1>A3>A4. 最优方案为A2. 表明本文提出的方法能够处理属性权重和自然状态发生概率信息均不完全的情形.

4 结 论