飞行器特性对雷达探测跟踪的影响
刘关心
(中国人民解放军92419部队,辽宁 125106)
1 引 言
雷达系统对目标的探测与跟踪总是要依赖目标自身的特性,理论和工程实践中以电磁散射能力表征雷达目标特性。对于飞行器的特性,人们普遍关注的是其运动特性,运动会使雷达目标特性发生变化。显然雷达目标特性、运动特性对雷达系统探测跟踪都有着直接的影响,且彼此间还相互关联,分析研究它们之间的关系是飞行器设计、目标特性研究、雷达工程、制导控制等领域需要深入开展的工作之一,本文对此进行了一些有益的分析与探索,提出了一些基本的观点与结论,供相关专业技术人员参考。
2 飞行器雷达目标特性分析[1]
雷达散射截面积(RCS,用б表示)是表征目标对照射电磁波散射能力的物理量,RCS是雷达自身、传播媒介与目标特征等综合特性的反映,雷达的探测跟踪要靠目标对电磁波的散射来实现,雷达方程用数学方法表现了该物理过程。
雷达方程简单形式见公式(1)
(1)
式中:Rmax——雷达最大探测距离;Pt——辐射功率;Gt——天线增益;Ae为有效接收孔径面积;Smin——最小可检测信号。从式(1)中可以看出:
(1)Pt、Gt、Ae由雷达自身性能决定,б、Smin与目标的特性相关,目标特性需要通过RCS幅值和信号噪声变化在雷达探测与跟踪中显现出来,因此RCS成为雷达目标特性的代名词。
(2)对于某一特定的雷达系统,雷达最大探测距离会随着RCS大小变化而增减,从定量的角度确定了RCS与雷达性能的联系,这既反映了雷达设计的特性,也反映了雷达对目标特性的要求。
(3)从雷达方程可以反推出RCS的计算方法,从雷达测量的角度确定了RCS的度量方法,这也正是雷达与雷达目标特性之间不可分的具体体现。
雷达的探测跟踪通过观测目标回波来实现,实际的雷达系统其雷达回波总会出现起伏,这种起伏与雷达目标的RCS变化相关联。根据现代雷达信号研究的成果,RCS的起伏特性呈现以下主要特点:
(1)RCS起伏是随机的、不规律的,通过统计学原理分析,可以用统计模型来描述其基本规律,现代雷达目标的RCS起伏一般服从χ2分布、莱斯分布和对数正态分布,这使得RCS的变化对雷达探测跟踪变得有规律可循、有数据可度量。
(2)雷达目标的复杂性导致形成多个散射源,在雷达视线坐标系下随着目标姿态的改变,雷达系统将接受不同的散射源信号,出现RCS变化,姿态改变越快RCS变化也越快,即RCS随目标姿态变化十分敏感。
(3)RCS起伏变化表面上出现回波起伏,实际上将导致发现概率、虚警概率、信噪比等雷达主要性能发生变化,影响探测跟踪能力。通过统计模型得到RCS概率密度后,可以估算出发现概率、虚警概率等,为雷达的设计使用提供依据。
3 飞行特性对雷达目标特性的影响
3.1 对RCS幅值的影响[2,3]
RCS是目标的固有特性,在某一状态下,其值是一定的,它不会随其它外部因素而改变,但不同状态下其RCS值是不同的。雷达的频率、极化方式以及目标空间姿态等是决定RCS的主要状态条件,这些条件改变时RCS也会发生变化,图1给出了战斧巡航导弹的RCS随方位分布情况。

图1 战斧巡航导弹RCS随方位分布Fig.1 RCS distributionof Tomahawk cruise missileat any Azimuth
对于运动的飞机和导弹类目标,空中的运动时刻改变着其相对雷达的空间姿态,对探测跟踪雷达而言,其RCS在随时间不断地发生着变化,形成RCS随时间起伏的函数。图2给出了某一飞行航路RCS随时间变化的情况。

图2 按航路飞行时RCS随时间变化Fig.2 RCS changes with time on the flight routes
从图1与图2的描述可以看出:
(1)同一目标不同方位其RCS差异较大,其起伏范围在(30~40)dB,雷达在不同方位探测跟踪目标差异很大,对雷达制导影响严重。
(2)雷达采用不同的频率和极化方式其RCS有较大差异,但起伏的规律是基本一致的,RCS的峰值点和波谷点的方位基本相同,说明雷达自身性能改变的是RCS幅值,而目标自身特性决定了RCS变化规律。
(3)图1中给出的是RCS随方位变化的情况,实际上,俯仰和横滚发生变化时也会呈现相同的变化,只是其起伏分布不同而已。这说明空中目标姿态的任何变化都会使RCS出现差异,三维姿态的变化使这种差异更加复杂,定量的评估也更难。
(4)图2的动态实测数据更具不稳定性,表明了RCS动静态之间的差异,为更有效判明雷达跟踪效果应以动态测试数据为依据[4]。
3.2 对雷达目标噪声的影响[3]
雷达目标噪声是由复杂形状目标的运动或姿态角变化产生的,复杂目标各部分散射回波幅值与相对相位变化会引起回波幅值的变化,而散射回波幅值是姿态角的敏感函数,无论目标轨迹还是姿态发生改变都将使雷达测量坐标系下的视线角变化,回波幅值的变化和视线角的变化形成雷达目标噪声,对雷达的测量产生影响。目标的不同特性能够产生幅度噪声、角闪烁噪声、多普勒噪声和距离噪声等主要雷达目标噪声,这些噪声以不同的形式影响雷达的探测跟踪性能。
幅度噪声是由复杂目标各散射子矢量引起的回波起伏,包含了低频到几千赫兹的频谱范围,对预警雷达的检测概率、跟踪雷达的角跟踪精度等产生影响。可视为刚体的飞行器,运动时姿态的变化或雷达视线变化,造成回波幅度的起伏,是主要的幅度噪声。飞行器翼尖等处的低频颤动,活动部件(螺旋桨、直升机旋翼、发动机排气道叶片等)调制特性,它们的基波和谐波分量将引起回波幅度的起伏或增加背景噪声,形成幅度噪声。显然,目标结构越复杂,回波幅度变化越大;目标机动或快速运动导致姿态或雷达视线变化快,幅度噪声就越大,反之亦然。因此,目标的结构复杂性、运动速度、机动性产生幅度噪声影响。
凡目标尺度能与波长相比拟,且具有两个以上等效散射中心的扩展目标,都会产生角闪烁噪声,用离目标几何中心的线偏差来表示。在远距离该线偏差几乎与目标速度、距离、雷达频率等不相关,对角跟踪误差影响较小。但对于近距离和高精度雷达跟踪,特别是雷达导引头,角闪烁噪声成为主要的误差源。对于对称目标产生的角闪烁线偏差均方值一般取(0.15~0.35)L(L为垂直视线方向的目标拓展长度),但实际上有可能超过L。角闪烁噪声所引起的角度误差与距离成反比,其影响主要在近距和中距上。可见,造成角闪烁噪声的主要是目标的尺度和等效散射中心,而在雷达视线目标下目标的运动会改变目标的展宽与散射中心,外部结构、尺寸及目标运动影响角闪烁噪声的形成。
任何扩展目标的机动或加速运动产生径向非线性运动,形成回波相位变化率,这一变化率与点目标变化率存在差异,即多普勒噪声。多普雷噪声主要是扩展目标回波相位波前畸变或目标上活动部件产生。回波相位波前畸变与角闪烁密切相关,经分析研究,由此产生的多普勒调制频率均方根值按公式(2)计算。
δf=2.72бεбθ
(2)
式中:бε=4πεθ/λ——角闪烁均方根;εθ——角闪烁线偏差;бθ——视线角变化率。由该式可见目标的运动速度、机动性、目标结构等特性都将影响多普勒噪声的形成。目标上的活动部件周期性旋转产生的调制谱分量同样是重要的多普勒噪声,该部分噪声与活动部件(如直升机旋翼)的转速、叶片数量等特性相关。
距离噪声是由扩展目标在视线方向的径向尺度造成回波展宽,形成测距误差,经验分析距离噪声均方根估计在(0.3~0.5)L′(L′为目标径向长度),它与角闪烁线偏差分布相似,由于目标运动与状态变化纵向比横向要小,距离噪声要比角闪烁噪声小。目标在运动过程中径向尺度在不断改变,距离噪声也会发生变化,与目标的运动状态等相关。
4 运动特性对雷达探测性能的影响
4.1 飞行状态对雷达探测能力的限制
雷达的探测首要的条件是无线电通视,飞行目标只有在雷达视线内才能被跟踪。飞行器飞行状态对雷达探测范围的影响主要是指其飞行高度和速度对雷达可视范围和可能探测跟踪时间,表1给出了目标飞行高度与视距及飞越视距时间的计算结果。
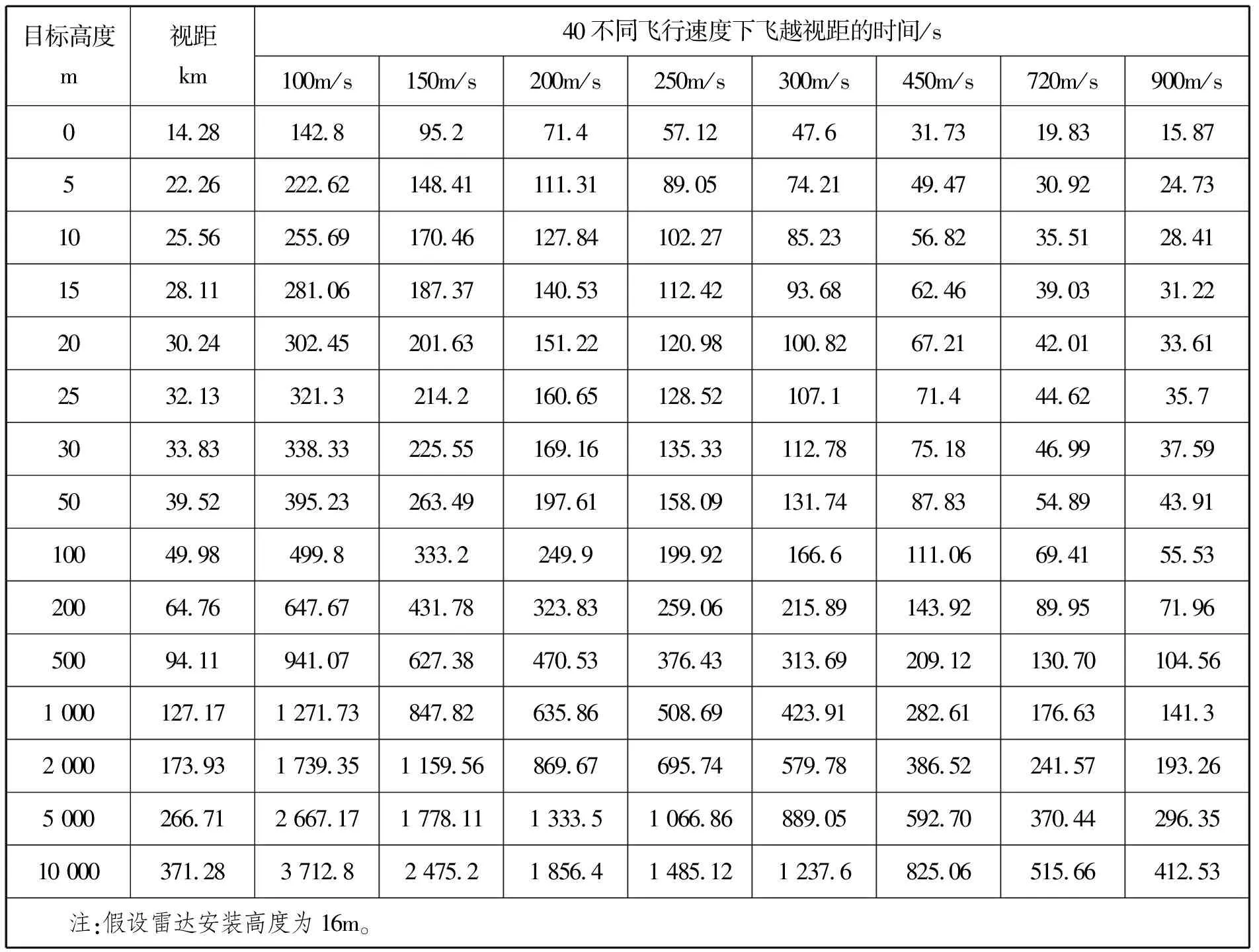
表1 飞行高度与视距及飞越视距时间Tab.1 Visual range and flight time of sight distance at diffident flight height
分析上表给出的数据,可以看出:
(1)目标的飞行高度和飞行速度对舰载雷达的探测跟踪有着严格的限制。飞行高度越低视距越小,雷达可探测跟踪的范围越小,飞行速度越快目标飞越视距的时间越短,雷达可用的探测跟踪时间也越少。雷达探测范围越小、可用探测跟踪时间越短,舰空武器使用就越受到制约。这也是飞行特性对舰空武器影响最本质之处。
(2)在目标常使用的特性下,视距并无实质的差距。反舰导弹飞行高度常在(5~25)m内,而视距差别只有10km左右,飞机目标常在中高空飞行视距的限制并不大。但对不同速度而言飞越视距的时间差距较大,因此飞行速度的制约性更大。
(3)表1中给出的仅是视距的数据,实际上当目标飞行高度很低,舰载雷达形成负角度探测跟踪时,多路径效应、海杂波等也会形成对雷达探测跟踪的影响。
4.2 飞行性能对雷达探测概率的影响[1,6]
当雷达本身固有参数(如工作波长,发射频率等)和其它环境参数(如气象条件、海面状况等)以及目标运动参数确定时,雷达所需信噪比与探测概率、虚警概率之间具有如公式(3)关系
lnPd=lnPfd/(SNR+1)
(3)
式中:Pfd——虚警概率;Pd——雷达探测概率;SNR——信噪比。当虚警概率Pfd为固定值时,雷达探测概Pd只和信噪比SNR有关系,而信噪比SNR会受到大气衰减、海杂波、多径效应以及入射角等因素变化的影响,当目标高度不同时,上述几种因素值会有较大变化,具体分析如下:
(1)对正常大气来讲,高度每降低100m,大气压上升12hPa,温度提高0.55℃,相对湿度不变。因此从大气衰减的角度来讲,目标高度越低,大气衰减越大,信噪比SNR就越低,雷达对目标的探测概率也就越低;
(2)对低空目标来说,海杂波强度大,海杂波使得检测门限较高,影响雷达的目标检测性能。当目标RCS较小(小于1m2数量级)时,海杂波功率与目标回波功率相当,对雷达的检测性能起主导作用,当目标距离较近时,目标所在距离单元对应的电磁波入射角增大,使海面散射系数增大、杂波信号增强,导致检测门限提高,可能造成目标难以检测。因此,从海杂波角度来讲,目标高度越低,海杂波越强,雷达对目标的探测概率越低。
4.3 飞行性能对雷达跟踪性能的影响[5]
雷达系统对目标的跟踪能力主要体现在跟踪速度和加速度上,除相控阵体制雷达外,雷达跟踪速度和加速度是重要的性能。特别是近距离跟踪目标时,目标的角闪烁十分严重,对跟踪性能的影响也严重。
从雷达观测看,其最大舷角跟踪速度按公式(4)计算。
Wq=VmP/R2
(4)
式中:Vm——目标速度;P——航路捷径;R——目标距离。
仰角跟踪速度按公式(5)计算。
Wε=VmH/R2
(5)
式中:H——目标高度。从式(4)和(5)中可以看出:
(1)雷达跟踪特性与目标运动性能有着密切的关联。尽管雷达跟踪性能是固有特性,但其设计应受到目标运动性能的约束,而且在实际使用过程中,其跟踪误差、稳定度会随着目标运动性能的变化而改变。
(2)目标距离越近跟踪速度要求越大,近距离对雷达跟踪影响大。目标运动速度越大,跟踪速度要求越快,高速度对雷达跟踪影响也大。目标捷径越大、高度越高,角度变化越快,跟踪速度也会越大,大捷径、高高度对雷达跟踪影响也越大。
(3)目标运动性能对雷达跟踪的影响是综合的,每一航路的每一时刻都会有差异,总体的趋势是有规律的。
5 结束语
飞行器目标特性研究是一个十分广阔的领域,从不同的角度、不同层面分析都会有许多十分有益的成果,本文从目标自身特性出发进行了一些初步分析与研究,以期引发更深更多的研究成果涌现,为推动这一领域发展起到一定的作用。

