基于AIS的轨迹插值方法
周 鹏,陈金海,林乾锋,梅 强,黄鹏飞
(1.集美大学航海学院,福建 厦门 361021;2.船舶辅助导航技术国家地方联合工程研究中心,福建 厦门 361021)
0 引言
船舶自动识别系统AIS(automatic identification system)能够发射并接收船舶的动态信息和静态信息[1,4]。其中:动态信息包括船舶发出信息的时刻,该时刻船舶经度、纬度值,船舶航向,船艏向等[5];静态信息包括船舶长度、宽度,AIS天线到船首距离和左右舷距离等。AIS数据分析研究预处理[6-9]一般都包括对原始数据的插值[2],但常用的几种数值分析插值方法[10-11]并没有结合具体水域的交通状况,忽视了由于插值方法的不同带来的误差[12]。为了进一步提高插值精度,已有学者提出结合专业领域的插值方法[3]。王超等[13]提出了一种考虑船舶航速航向的AIS航迹插值方法,刘立群等[14]提出三次样条插值结合船舶经纬度的方法;Wang等[15]提出结合空间多个维度构建多维阵列来对轨迹进行插值。这些插值方法结合了AIS数据特有的属性,在一定程度上减小了插值方法本身造成的误差,但适用性有限。本文通过分析船舶轨迹研究中常用的插值方法,提出一种结合线性插值和航速航向[16]的新插值方法,并以实际AIS轨迹数据进行验证。
1 插值原理
1.1 常用插值方法
在船舶轨迹分析中常用的插值方法可以分为两种:一种是以数值分析为基础,常用的有拉格朗日线性插值、三次样条插值等;另一种是以数理统计结合AIS固有属性的方法,主要有结合时间的插值方法和结合航速航向的插值方法。
1)拉格朗日插值方法
拉格朗日插值法能给出一个恰好穿过二维平面上若干个已知点的多项式函数。如对实际的船舶轨迹数据进行处理,有若干个已知点,拉格朗日插值法可以得到一个多项式,能够包含所有的已知点,最后再由多项式得到插值点的数据。这种方法思路简洁,在算法的实现上也简单,但是由于AIS数据的离散性、连续变化的无规律性,这种插值方法精度并不高;而且AIS数据量大,根据拉格朗日插值方法构造插值多项式时,插值点越多,插值多项式的次数也越高,当插值次数过高时就会出现龙格现象(即在一定范围内能较好逼近,但越接近插值端点,误差也就越大的现象),这样得到的插值结果误差会很大,还会产生虚假的波动,不具备保形效果。
2)三次样条插值方法
三次样条插值(Spline插值)是通过求解三弯矩方程组得出曲线函数组的过程[17],最终得到的是通过一系列形值点的一条光滑曲线。三次插值样条曲线在灵活性和计算速度之间进行了合理的折中。与更高次样条相比,三次插值样条只需较少的计算和存储,且较稳定。与二次插值样条相比,三次插值样条在模拟任意形状时显得更灵活。
3)结合时间的插值方法
将船舶运动分解为经度和纬度两种运动状态的变化,即将原有的经纬度变化视为(时间—经度)(时间—纬度)两个一维运动的组合,将两种方向上的运动都视为短时间的匀加速直线运动。假设待插值点为pi(Loni,Lati,vi,θi,ti),其中:Lon代表经度;Lat代表纬度;v代表船速;θ代表航向;t代表发送时间。前后两点坐标为q1(Lon1,Lat1,v1,θ1,t1)和q2(Lon2,Lat2,v2,θ2,t2),由通过经纬度插值变为通过时间插值,通过插值时间序列T得到待插值时间ti点处的坐标(Loni,Lati),再结合线性插值方法分别对两种运动状态插值,最后将插值得到的相同时间的经纬度组合,得到最终的插值结果。
1.2 改进插值方法原理
船舶轨迹可分为直线轨迹段和曲线轨迹段,若插值点附近航向差值的绝对值在5°以内,则判定该插值点所处轨迹段为直线轨迹,否则为曲线轨迹[16]。
首先将AIS的大地坐标值(经纬度)经过高斯—克吕格投影转化为平面坐标值(x,y)[18];如果已知插值点前后点高斯坐标A(x1,y1)、B(x2,y2),那么可以分别以A、B两点为基准得到两组插值点的预测坐标
(1)
(2)
式中:θ和v分别为插值基点处的航向和航速;ti为插值点的时间,t1、t2为插值基点处对应的时间。
对预测坐标(xi1,yi1)(xi2,yi2)进行加权平均,权重由插值点距离A、B两点的时间差确定,距离哪一点时间越近,相应点对应的权重也就越大。即
Q1=1-(ti-t1)/(t2-t1),
Q2=1-(t2-ti)/(t2-t1)。
(3)
式中:Q1,Q2分别为A、B两端的权重,则加权平均后的插值点坐标为
(4)
最后将相应平面坐标转换为经纬度坐标,即得到最终的插值结果。
2 整体实验设计
为了验证改进后的插值方法的插值效果,利用MMSI码为412468324的船舶在20150104这天一段时长为20 min的AIS轨迹数据,在MATLAB中进行仿真实验。对这段轨迹分别采用不同插值方法进行轨迹插值,通过比较与原始轨迹的贴近程度,先验证各种插值方法在轨迹较完整时的效果,再从完整轨迹中取4个抽样点(表1中加黑的数据点),模拟极端稀疏情况下的AIS数据,通过比较不同插值方法,对同一数据插值后与原轨迹的接近程度来进一步验证其方法的优劣程度。
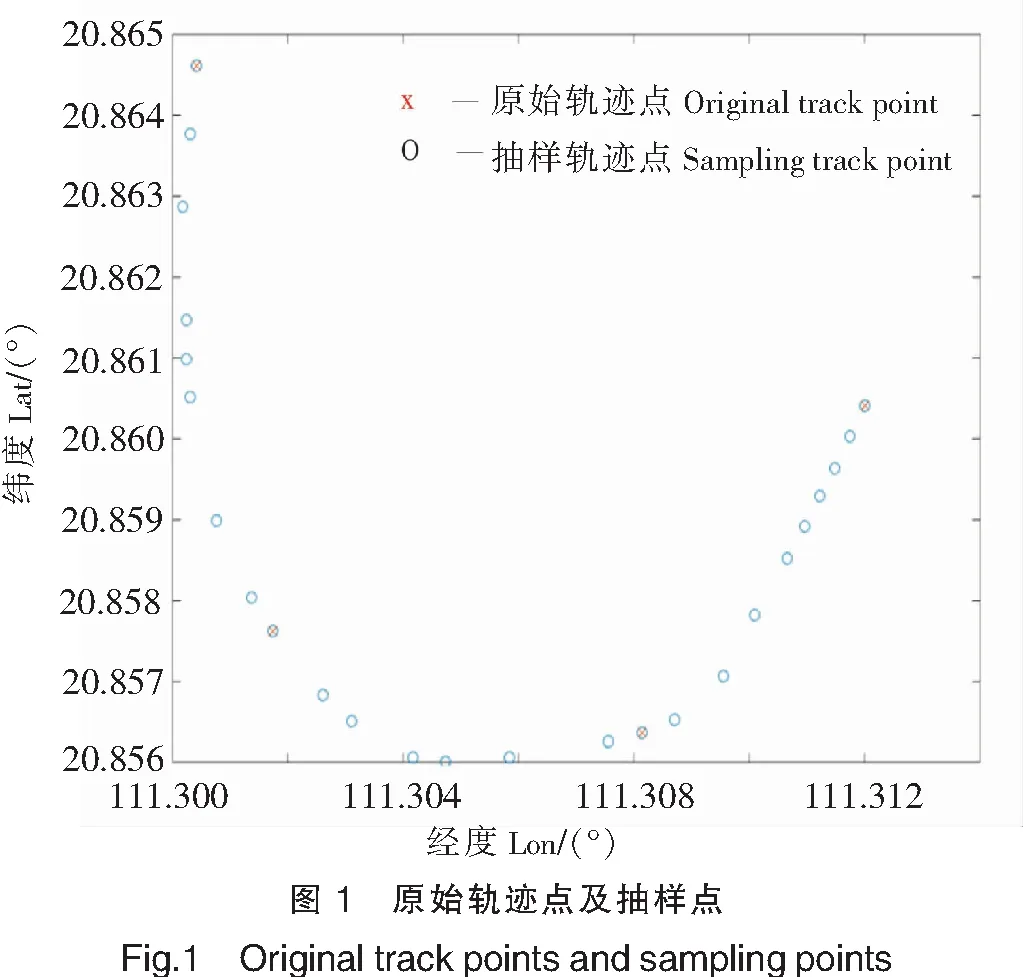
船舶AIS原始数据如表1所示(表中加黑的为抽样点数据)、对应的坐标图如图1所示(图中绿色点为抽样点)
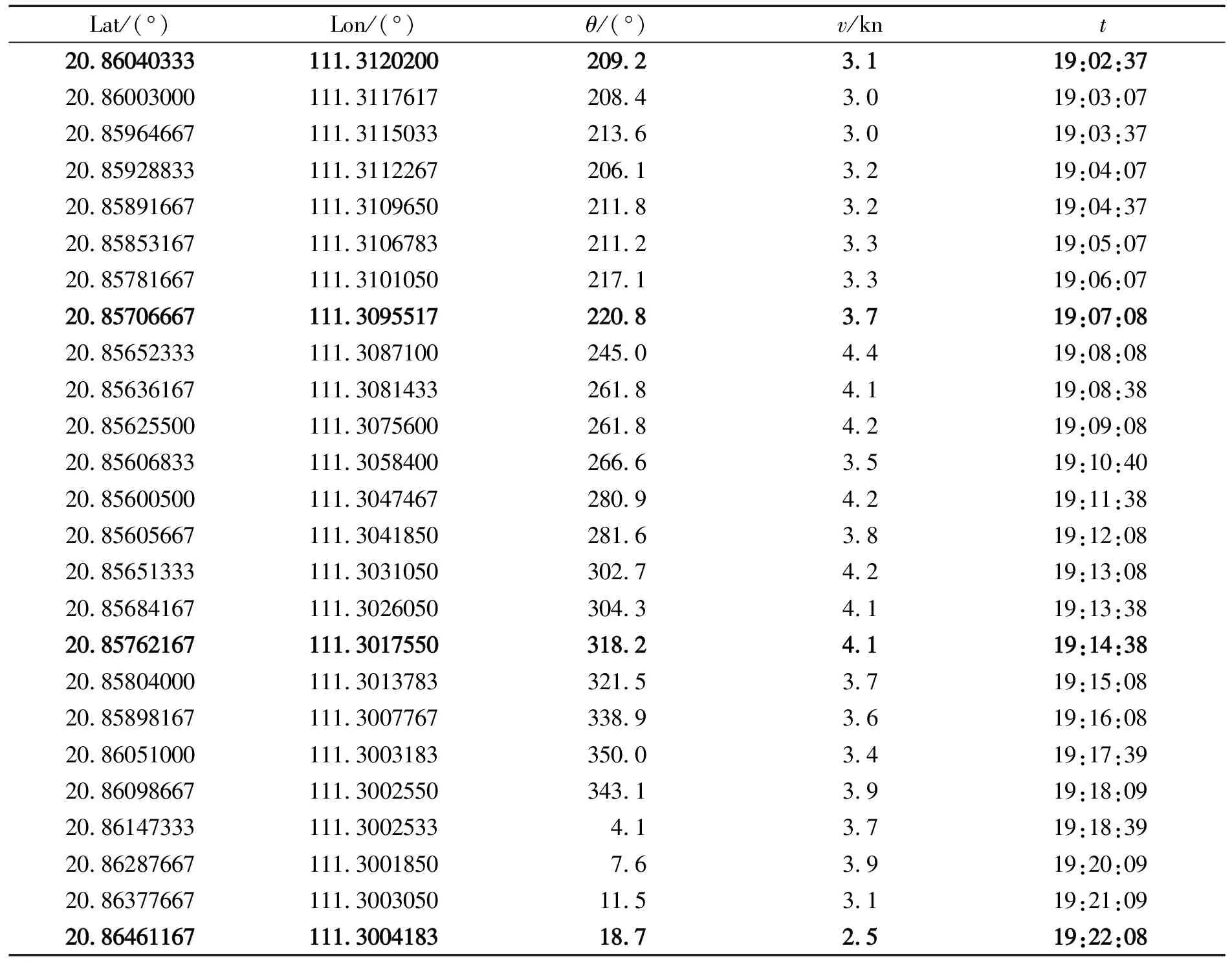
表1 原始轨迹数据
3 实验结果及分析
采用上述4种方法分别对原始轨迹点以及抽样点进行插值,并输出插值图像,直观对比插值轨迹与原轨迹的趋近程度,分析改进后的插值方法在曲线轨迹时的效果。
在对原始轨迹的插值过程中,4种插值方法的效果如图2所示,除拉格朗日线性插值轨迹较原始轨迹有较小幅度的偏差,其余3种方法都很接近原始轨迹。主要原因在于原始轨迹点较密集,这些方法的插值误差都很小。这也表明三次样条插值、时间维度插值、改进航速航向插值方法在原始轨迹密集的情况下都可以满足实验需求。
为了更进一步分析这4种插值方法的适用范围,在原始轨迹中提取4个抽样点,只以这4个点为已知,模拟稀疏情况下的船舶轨迹,输出结果如图3。
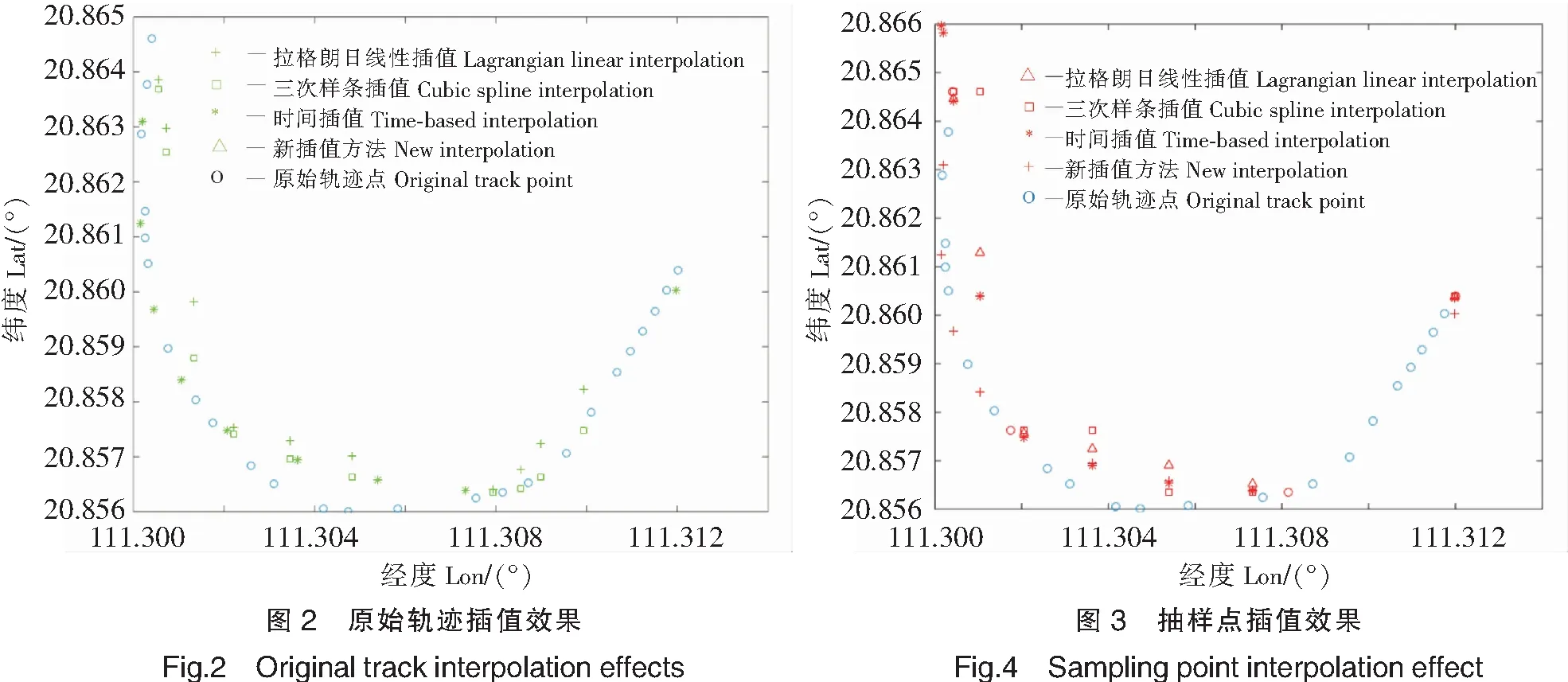
从图3可以看出,三次样条插值由于初始已知条件太少,插值得到的轨迹点发生跳变,轨迹的拟合度最差;拉格朗日线性插值就是将已知点相连作为拟合轨迹,插值点也在轨迹上对应取值,误差太大,且在插值过程中经常出现轨迹跨越陆地的情况,也不可取;基于时间的插值方法虽然在经度111.302°~111.308°区域内插值效果与改进后的插值方法精度相差不大,但在第一个抽样点到第二个抽样点范围内误差很大,并且由于原始数据时间间隔不统一,插值还出现了插在抽样点范围以外的情况;改进后的新插值方法在整体上拟合原轨迹效果最好,插值精度误差也最小,证明改进后的插值方法在弯曲稀疏轨迹段也能取得较为理想的效果。
通过对比这些插值方法,可以发现单纯以数值分析为原理的插值方法在AIS轨迹插值上效果并不理想,主要原因在于远海AIS数据稀疏,在插值时提供不了数值分析插值方法所需的大量临近已知点,并且AIS中的船舶轨迹数据点并不同于数学上的离散函数点,很难发现其数学意义上具有的函数规律,因此当AIS数据大量缺失时,轨迹插值的最好方法还是结合航速、航向、时间这些数据,将轨迹分类处理,直线轨迹采用数值分析方法插值,保质并且高效,曲线轨迹采用改进后的航向航速插值方法,其精度得到了明显提高。
4 结论
通过总结现有AIS数据的插值方法,提出一种用于海上交通研究分析的新插值方法。在前3种插值方法的基础上进行改进,将轨迹曲线分类处理,按照插值前后点间航向的变化,将轨迹分为直线和曲线两种轨迹段,直线轨迹段各插值方法精度区别不大,因此采用分段线性插值方法,插值精度和效率都能得到保证;曲线轨迹段插值较为困难,因此结合AIS航速航向以及时间这些属性,分别以两端点坐标和航速航向为基准得到两组预测差值坐标,再加入时间作为权重,实验结果表明插值坐标精度有了明显提高,并且在插值点前后时间间隔很长的情况下效果较其他方法更好,尤其在曲线轨迹的插值上也明显优于其他方法。因此此种新插值方法在船舶数据分析上具有一定的实际意义。

