电动汽车无线充电系统电磁场计算方法
王林梅,刘 瑞,蒋佐富,陈 鑫,周仲岳,张克涵
(1.台州宏远电力设计院,浙江 台州 318000;2.国网浙江省电力有限公司台州供电公司,浙江 台州 318000;3.西北工业大学,西安 710072)
0 引言
当前我国电动汽车产业已步入快速发展期,充电设施建设如火如荼[1]。电动汽车的无线充电技术可以解决火花、积尘、接触损耗及机械磨损等一系列传统充电方式所带来的问题,提高电动汽车的续航能力[2],因此电动汽车无线充电将成为未来主要的发展方向。
目前,无线电能传输技术主要有3种方式:基于磁耦合的IPT(感应电能传输)、基于电场耦合的CPT(电容能量传输)、微波辐射。基于磁耦合谐振的非接触式电能传输系统,在传输距离较远时也可以实现大功率高效电能传输;基于电场耦合的无线电能传输系统,结构简单,制造成本低,具有很大的发展空间[3];基于微波辐射的传输方式,其传输距离远远大于传输装置的几何尺寸[4],其缺点是传输效率较低。CPT及IPT技术均可应用到电动汽车无线充电系统中。IPT作为一种传统无线电能传输技术,原理简单,容易实现,因此在电动汽车无线充电领域具有广阔的应用空间。目前国内外在磁耦合无线电能传输方面的研究主要集中在阻抗匹配、系统动态控制、电磁兼容及生物安全问题等方面[5]。磁耦合谐振式WPT(无线电能传输)技术起步较晚,但近年来受到了较多的关注[6]。
1 IPT研究国内外现状
2007年,MIT(麻省理工)的科学家首先基于耦合模理论对磁耦合谐振WPT进行系统建模,分析传输距离、工作频率、天线结构参数对传输功率和传输效率的影响,然后分析耦合谐振的非辐射能量传输特性[7-8],为提高传输效率和增大传输距离,先后提出了2种改进的谐振器结构,即中继谐振器结构和多接收负载谐振器结构[9-10]。日本东京大学 Takehiro等通过等效电路和纽曼公式[11],实现传输效率的最优化。2008年,Intel公司的J.R.Smith展示了基于磁耦合谐振技术的研究成果,在演示过程中,该系统以75%的效率实现了60 W传输功率[12]。华南理工大学张波教授课题组从电路角度分析系统传输效率与线圈尺寸、距离等之间的关系,从而进行无线电能传输系统优化设计[13]。东南大学将无线传输的距离增加到50 cm左右,传输功率大于1 kW[14]。
目前对于IPT系统,多采用互感模型进行分析,这种分析方法只能定量地表示出次级线圈感应电压和感应电流,进而得出输出功率,但这种方法并不能分析系统参数对系统性能的影响,无法具体分析系统传输机理,难以对系统耦合线圈进行优化设计。因此本文采用电磁场分析方法,首先利用电磁场的矢量叠加原理,推导得出多匝线圈产生的电磁场解析表达式,从而得出WPT系统初、次级侧线圈产生的合成电磁场解析表达式,并应用COSMOL仿真软件和WPT实验系统,验证了电磁场解析表达式的正确性,对WPT系统的传输机理进行了深入研究。
2 IPT基本原理
应用磁耦合谐振IPT技术对电动汽车进行无线充电,其基本原理为:汽车停车位下面的初级侧线圈产生交变电磁场,在汽车底盘安装的次级侧线圈感应出交变电流,经过AC/DC(交流/直流)以及DC/DC(直流/直流)变换,转换为满足电池充电要求的直流电,电路模型如图1所示。
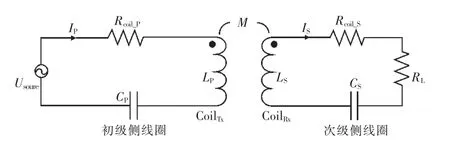
图1 串串型电路模型
其中,LP和LS分别为初级侧、次级侧线圈自感;M为两线圈之间的互感;CP和CS分别为初级侧、次级侧补偿电容;Rcoil_P和Rcoil_S分别为初级侧及次级侧线圈交流阻抗;RL为负载阻抗;Usource为电源。在初级侧、次级侧均达到谐振状态时,传输效率η和功率PL表示如下:
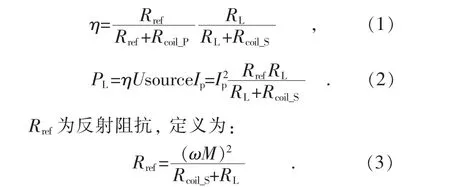
3 电磁场计算
一般而言,线圈采用的结构可分为螺旋线圈结构和平面线圈结构,多匝线圈的结构如图2所示,线圈半径为a。
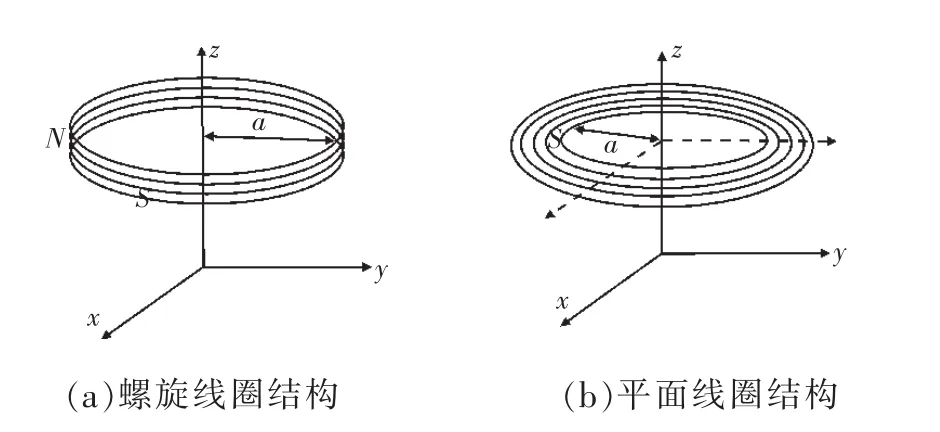
图2 多匝线圈结构
空间中平面线圈和螺旋线圈是轴对称的,其产生的电磁场在空间中也具有对称性,可以由单匝线圈产生的电磁场的解析表达式,来研究多匝线圈在空间产生的电磁场分布状况。因螺旋线圈与平面线圈解析表达式的推导方式基本相同,本文仅推导螺旋线圈在空间中产生电磁场的解析表达式,然后建立相应的仿真模型,搭建实验系统,验证解析表达式的正确性。
3.1 单匝线圈
如图3所示,选螺旋线圈中轴线与z轴重合,t=0时刻初级侧线圈电流方向和轴正向呈右手螺旋关系O-ρφz,建立线圈柱面坐标系,电流的时域表达式为 i(t)=Icos(ωt)。假设通电线圈处于线性均匀的无限介质中,ε,μ,σ分别表示介质的介电常数、磁导率和电导率[15]。
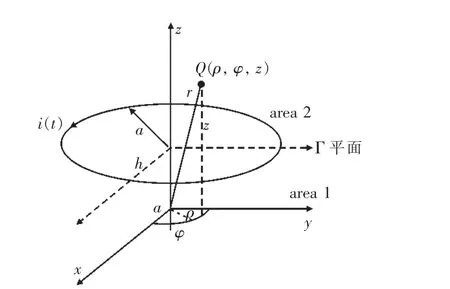
图3 单匝通电线圈柱面坐标系
图3中线圈半径为a;r表示原点O与任意点 Q(ρ,φ,z)的间距。通电线圈处于 Γ(z=h)平面上, 规定 z<h区域为 area 1,z>h区域为 area 2,即在area 1和2内没有电流源的分布,电流源仅分布在area 1和2的边界处。
空间中任意一点 Q(ρ, φ, z)处电场强度 E(ρ,φ,z)为[16]:
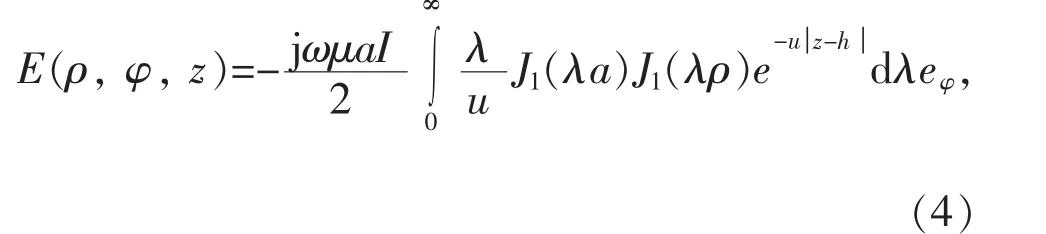
由电场强度E和磁场强度H的关系,可得Q(ρ, φ, z)处磁场强度 H(ρ, φ, z)为:
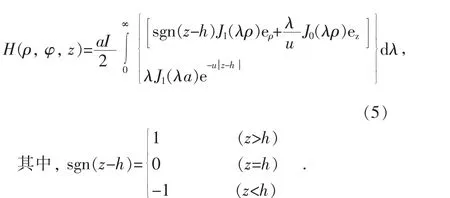
3.2 N匝螺旋线圈电磁场计算
N匝螺旋线圈可以看作图4中灰色单匝线圈沿z轴方向平移(N-1)次得到,单次平移间距为s,螺旋线圈可以分解成N个单匝线圈。N和a分别表示通电线圈的匝数以及半径,Q(ρ,φ,z)表示柱面坐标系中任意一点,r表示坐标原点O到Q点的距离。根据单匝线圈产生的电场强度公式(4),可以推导出灰色单匝线圈沿z轴平移(N-1)s之后,在Q(ρ,φ,z)处产生的电磁场解析表达式,将多匝线圈产生的电场强度和磁场强度做矢量叠加,可以得到N匝螺旋线圈在Q(ρ,φ,z)产生的电场强度 E(ρ, φ, z)和磁场强度 H(ρ, φ, z)解析表达式为:
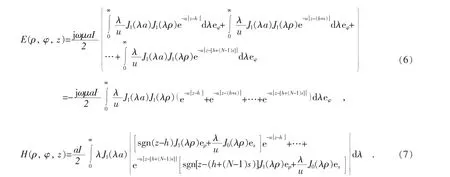
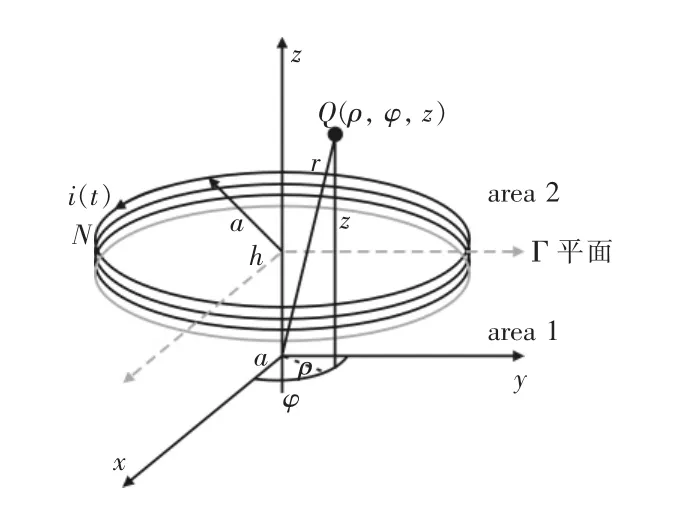
图4 螺旋线圈柱面坐标系
3.3 WPT系统电磁场计算
在空间中的电场和磁场是初、次级侧线圈产生的电场和磁场的矢量叠加,建立螺旋线圈柱面坐标系如图5所示,Nj和aj分别表示线圈匝数和内半径,hj表示线圈平面与z=0的xoy平面的垂直距离,Q(ρ,φ,z)为任意一点,rj是坐标原点O到Q点的距离,其中j=p时表示初级侧线圈的参数,j=s时表示次级侧线圈的参数。

图5 螺旋线圈结构初、次级侧线圈柱面坐标系
当位于多匝线圈的单侧时,式(6)、式(7)可化简为式(8)、 式(9):
空间中电场强度Etotal和磁场强度Htotal是初级线圈产生的Ep,Hp和次级侧线圈产生的矢量和,由式(8)、式(9)可得到在areaⅡ区域电磁场解析表达式(10)、 式(11):

4 仿真验证
采用有限元分析软件COMSOL搭建仿真系统,对螺旋线圈构成的WPT系统电磁场解析式进行仿真分析,验证解析表达式的正确性。根据上节推导可知,电场强度和磁场强度与φ无关,选取φ=0截面进行仿真分析。
4.1 电场强度
取φ=0截面中任意一条直线上的E解析值与仿真值进行比较,线圈参数如表1所示。取φ=0,ρ=60 mm,10 mm≤z≤60 mm, 利用 COMSOL进行仿真,再使用式(6)计算出解析值,作出电场强度幅值和相位图,如图6和图7所示。

表1 螺旋线圈参数
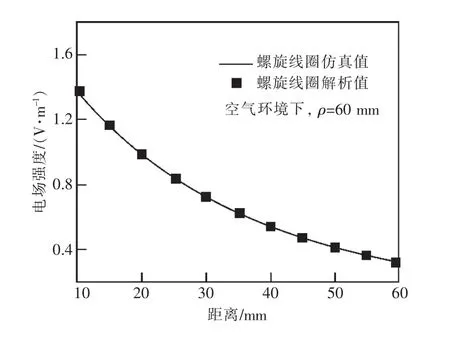
图6 电场强度幅值
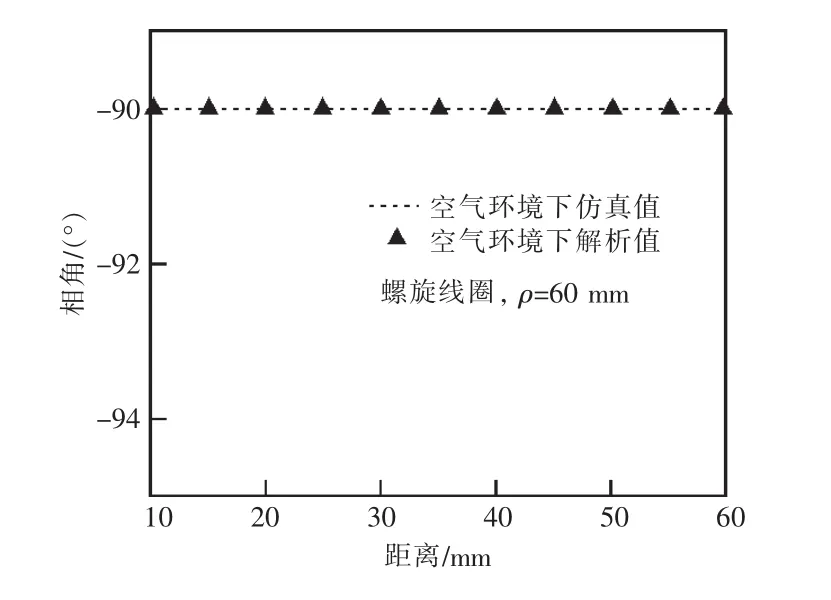
图7 电场强度相角
从图6和图7可以看出,电场强度的幅值和相角的解析值以及仿真值非常接近,从而验证了螺旋线圈电场强度E解析式的正确性。
4.2 磁场强度
为了验证磁场强度的解析式,令ρ=60 mm,z从10mm到60 mm变化,利用COMSOL计算出螺旋线圈产生的磁场强度仿真值,参数如表1所示,利用式(7)得出磁场强度解析值,其对比如图8所示。
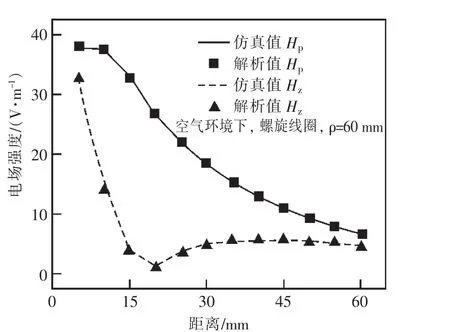
图8 空气中螺旋线圈产生的磁场强度对比
H在空间中只有ρ和z方向上的分量。根据图8可知,仿真值和对应的解析值吻合很好,说明螺旋线圈在空间任意一点产生的磁场强度解析式是正确的。
5 实验验证
通电线圈在空间中产生交变电磁场,线圈在交变电磁场中感应出的电压Uopen是线圈所在处E的环路积分,表达式为:

利用示波器的电压钳测量感应线圈电压值,利用有限元分析软件建立线圈模型,得出感应电压仿真值,通过式(12)算出感应电压解析值,比较实验值、仿真值以及解析值,验证式(10)电磁场解析表达式的正确性。
5.1 单线圈电场试验验证
初级侧线圈通入正弦交变电压,次级侧线圈保持开路,保持初级侧电路电流为1.5 A,同时改变电流频率,使用示波器测量次级侧开路线圈感应电压,电路拓扑结构如图9所示,线圈参数如表2所示。作出感应电压Uopen实验值、仿真值及解析值的对比曲线,如图10所示。
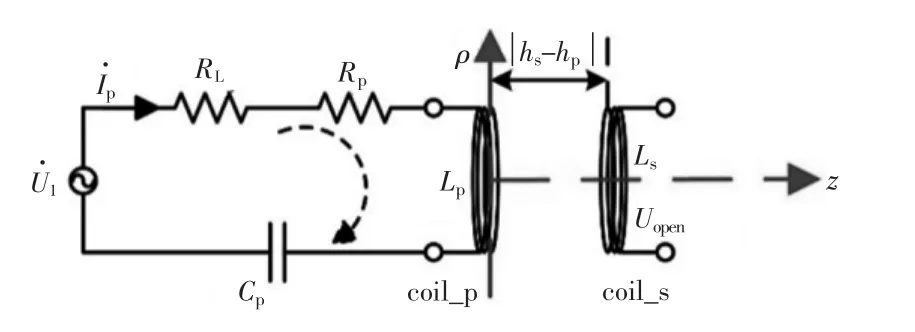
图9 单线圈通电电磁场验证拓扑结构
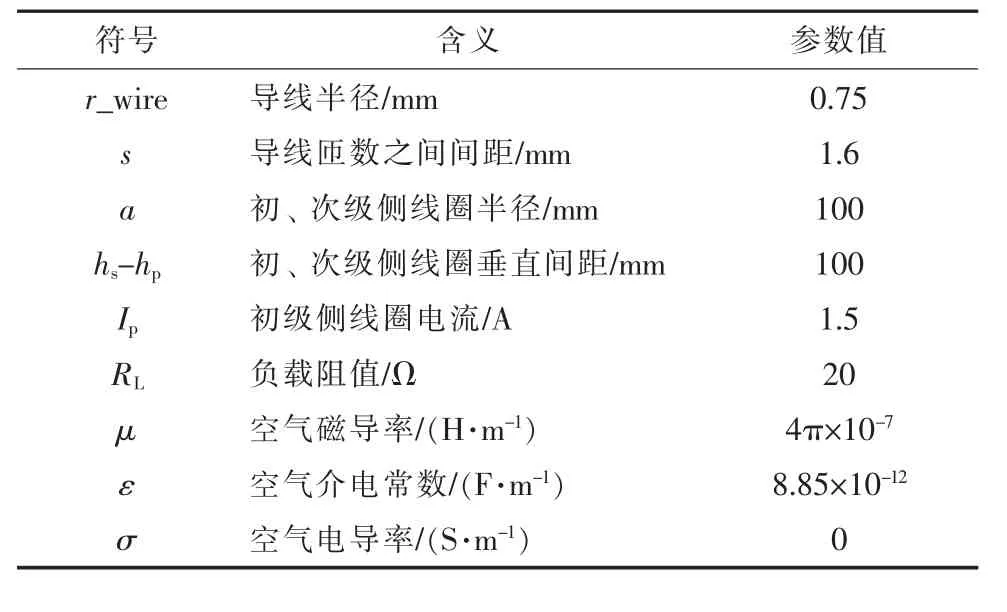
表2 通电线圈参数
对图10分析可知,五角星(★)对应的是解析值,空心圆(○)代表的是实验测量值,而直线或者虚线代表仿真值,对应着不同线圈的匝数。解析值、测量值及仿真值均非常接近,验证了式(8)螺旋线圈电场强度解析式的正确性。
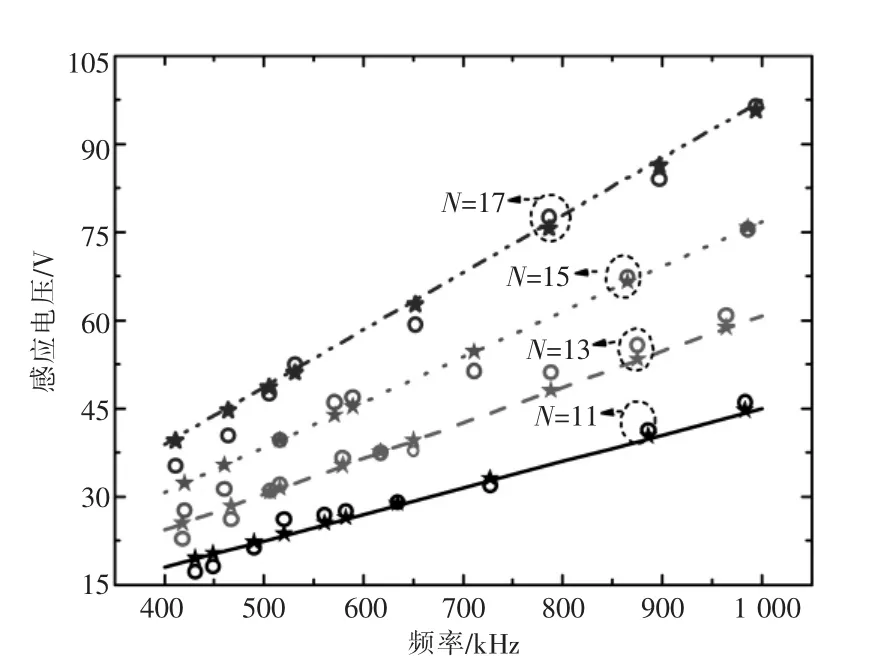
图10 开路线圈感应电压
从图10可以明显看到,匝数越大,次级侧线圈感应电压Uopen越大,一方面是因为初级侧线圈匝数越大,在电流一定的情况下,产生的电场强度越强;另一方面次级侧线圈匝数变多,从而感应电压相应增加。匝数固定时,次级侧线圈感应电压Uopen随频率的增大而增大。感应电压的变化规律与电场强度解析表达式相符合。
5.2 WPT系统电场试验验证
当初级侧线圈通入正弦交变电压后,在空间中会产生交变电场Ep,当次级侧线圈回路接通,形成电流回路,在空间中产生另一个交变电场Es,与Ep矢量叠加,从而形成新的电场Etotal。在初、次级侧线圈中间放置一个同轴开路单匝线圈,线圈感应电压U的解析式为:
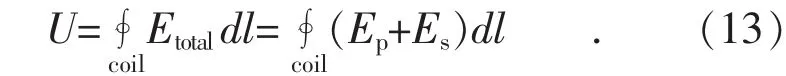
实验系统拓扑如图11所示,线圈参数如表3所示,当初级侧线圈电流频率为500 kHz时,对单匝线圈进行平移,测量不同位置的感应电压,同时作出感应电压变化曲线,如图12所示。
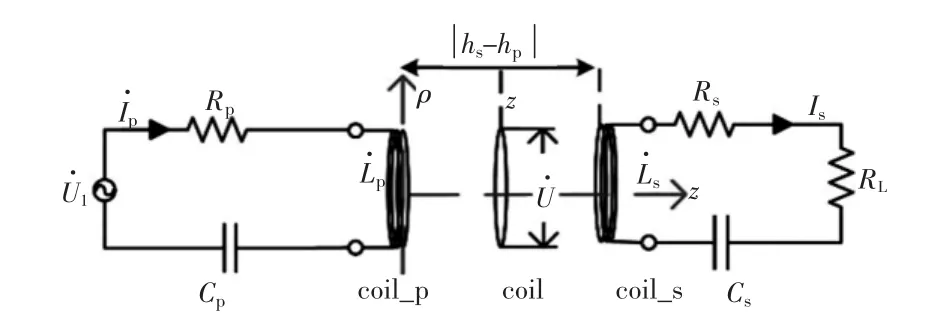
图11 WPT系统拓扑

表3 通电线圈参数

图12 线圈感应电压
从图12可以看出当匝数和频率固定时,初级侧线圈和次级侧线圈之间随着单匝线圈位置的改变,由初级侧线圈和次级侧线圈分别产生的交变电场随之改变,经过电场叠加,单匝线圈感应电压发生变化。圆点(●)和菱形(◆)分别代表实验值和仿真值,直线代表解析值,相同参数下实验值、解析值以及仿真值互相吻合,证明了式(13)的正确性,从而证实了系统电场强度解析表达式(10)的正确性。由于电场强度与磁场强度有固定的约束关系,也间接说明磁场强度的解析表达式(11)是正确的。
6 结语
本文首先利用电磁场的矢量叠加原理,推导得出多匝线圈产生的电磁场解析表达式,从而得出WPT系统初、次级侧线圈产生的合成电磁场解析表达式。随后应用CPOSMOL仿真软件,进行了仿真分析,仿真值和对应的解析值吻合很好,说明电磁场解析表达式的正确性。最后搭建WPT实验系统,进行实验验证,证明了提出的电磁场分析方法的正确性,为相关系统参数优化提供了参考。

