考虑电网日常无功投切的低频振荡阻尼在线预警方法

黄弘扬，彭 琰，郑 翔，华 文，楼伯良，余一平

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.国网浙江省电力有限公司，杭州 310007；3.河海大学，南京 210098）

0 引言

区域电网互联是跨区大范围资源优化配置的客观要求，同时也是世界各国电网发展的总体趋势。区域电网互联可以带来跨区电力输送、水火电互济、削峰填谷、备用容量需求降低、事故紧急功率支援等诸多好处，可以显著提高电网运行的经济性和可靠性。但是由于电网规模的不断扩大，区域互联电网的网架结构和运行方式日趋复杂，电网安全稳定分析与控制难度必将大为增加，其中较为突出的便是互联电网的低频振荡问题[1-2]。

及时获得系统的阻尼状况，实现电网低频振荡的预警预控，对电力系统安全稳定运行具有重要意义[3-7]。以往系统阻尼一般通过典型方式离线模态分析或者基于实时潮流和动态模型参数匹配后的在线模态分析获得，其结果极大地依赖于系统潮流和模型参数的准确性。而在低频振荡在线监测方面，则是主要基于PMU（同步相量测量单元）实测数据，对系统发生振荡后的动态轨迹进行Prony（普罗尼算法）分析，获得系统振荡模式信息[8-10]。但是由于实际电网大幅功率振荡发生较为偶然，当实际低频振荡事故发生时进行在线辨识和分析，难以实现预警和预控的目的。当前强迫功率振荡现象在电网中时有发生，在强迫功率振荡情况下，动态振荡轨迹的Prony分析结果难以反映系统真实阻尼状况[11-13]。因此，有学者提出基于系统日常运行过程中时刻存在环境激励的类噪声信号，通过ARMA（自回归滑动平均）方法在线获得系统功率振荡特性[14-18]。类噪声信号中虽然含有部分反映系统模式的自由振荡信号，但是由于不知激励的具体形式，响应信号较弱，容易受其他噪声信号的干扰，从而造成误判，而且存在所需观测时间过长，实时性欠缺等问题。因此，如何准确实时地获得系统的真实阻尼状况达到预警目的亟待研究。

实际上，电网中每天都存在一些典型的有功和无功日常扰动，例如大容量电容器投切就可激励邻近机组电磁功率振荡。本文利用这种电网日常扰动，提出通过日常无功投切后对自由振荡轨迹进行阻尼辨识，以实现电网低频振荡阻尼在线预警。这种方法与传统类噪声信号阻尼辨识方法相比，由于其已知激励的具体形式，响应信号较强，故不易受噪声干扰而误判。浙江电网实测数据的分析结果也验证了所提出方法的有效性。

1 基本原理

1.1 单机系统分析

以经典单机无穷大系统为例，说明电网无功投切对低频振荡的激发作用。如图1所示，图中发电机采用经典模型，发电机内电势用Eg表示，内电势功角用δ表示，机端电压用Vt表示，机组有功功率和无功功率分别用Pe和Qe表示；节点2为负荷节点，假设存在冲击性的负荷扰动（ΔPd，ΔQd），节点电压为Vd，电压相角用θd表示；节点3为无穷大节点，节点电压为Vs。节点注入功率方程线性化后可以表示为：

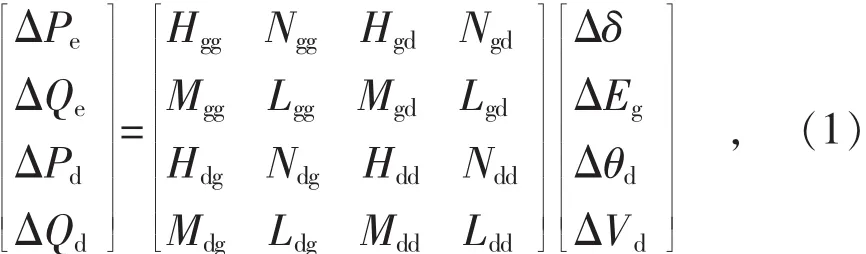
式中：H，N，M，L 分别为 Pe，Qe，Pd，Qd对 δ，Eg， θd， Vd的偏导数。

由于经典模型情况下ΔEg=0，可以求得：

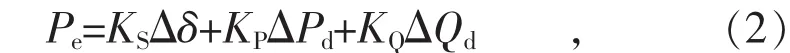
式中：KS为发电机同步转矩系数；KP和KQ分别为与有功负荷扰动和无功负荷扰动相关的系数，均为实数。

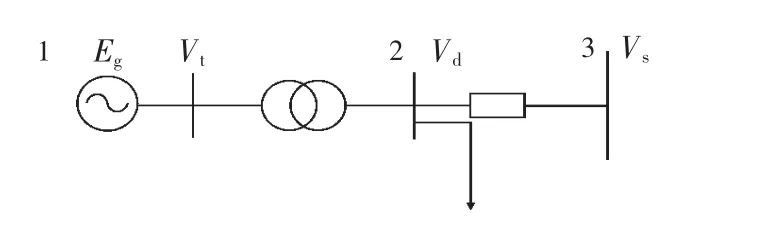
图1 单机无穷大系统示意

由式（2）知，冲击性的有功负荷和无功负荷都会使电磁功率存在冲击性的分量。为便于分析，本节假设仅存在电容器投切情况，即假设ΔPd=0， ΔQd=Fε（t）， 其中 F 为阶跃幅值， ε（t）为阶跃函数。下面分析阶跃无功负荷冲击下的机组响应特性，发电机线性化转子运动方程为：

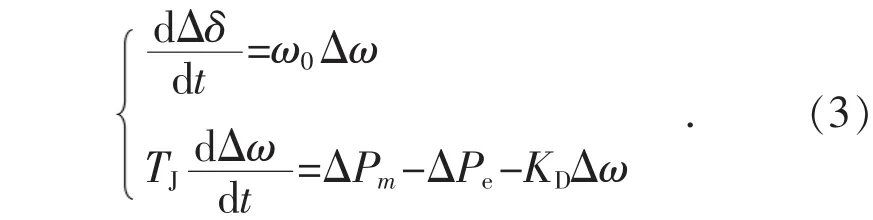
忽略机械功率，使ΔPm=0，得：

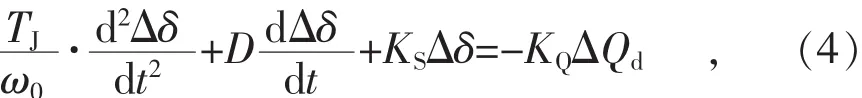
式中： ΔQd=Fε（t）为电容器扰动； ω0=2πf0， f0为系统基准频率；Δω为发电机转子角速度偏差；ΔPm为发电机机械功率偏差；TJ为发电机惯性时间常数；D=KD/ω0为发电机阻尼系数。

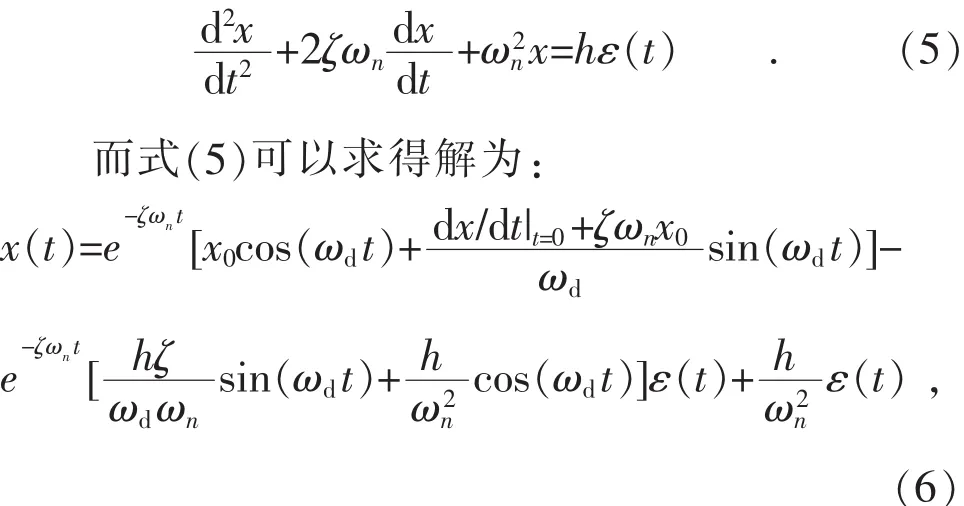
由式（6）可以看出，在电容器投切造成的无功负荷阶跃冲击下，邻近发电机状态变量时域响应主要为系统固有振荡模式的自由振荡分量。

1.2 多机系统分析

假设网络中l节点存在无功负荷扰动，根据网络分析理论推导可得：

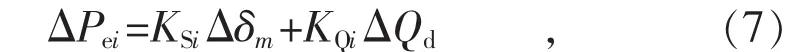
式中：ΔPei为发电机电磁功率偏差；Δδm为发电机功角偏差；KSi为同步系数；KQi为电容器投切扰动无功功率机组分配因子，表示机组电磁功率变化中与电容器投切扰动直接相关部分的系数，其大小由电容器与机组间的电气距离决定。

忽略发电机机械功率变化，并将式（7）中ΔPei带入发电机线性化转子运动方程，可得：

式中：u=ΔQd；B=[0 … KQ1… KQm]T。

根模态分析推导，可得系统状态变量解为：

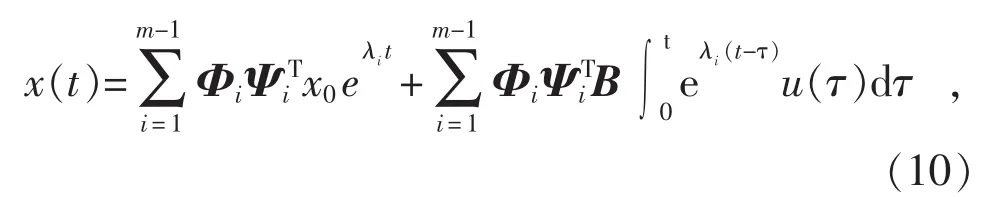
式中：Φi和Ψi分别为第i阶模式的左、右特征向量。

根据式（7）、式（10）并结合参与因子含义，可得出如下结论：阶跃负荷距离机组的电气距离越近，阶跃变化对该机组施加的振荡激发作用越大。在多机系统情况下，当距离电容器/电抗器电气距离较近的发电机组是某些关键振荡模式的强相关机组时，电容器/电抗器阶跃冲击可能激发这些关键模式的小幅振荡，并在机组电磁功率动态响应中存在该模式的自由振荡分量。通过对这些自由振荡分量进行在线监测和辨识，可以获得系统相关关键模式的实时阻尼信息。

2 方法步骤

由前述分析可知，电网日常电容器/电抗器等无功补偿设备的投切可激发某些关键振荡模式，用于电网低频关键振荡模式阻尼在线预警，其具体的实施步骤如下：

（1）关键模式辨识：基于实时潮流和动态数据进行在线模态分析，并结合电网历史功率振荡数据，确定系统关键振荡模式和强相关机组。

（2）阻尼监测机组选择：选择关键振荡模式的强相关机组为阻尼监测机组。强相关机组更易激发关键振荡模式，而且机组振荡信息更明显，有利于阻尼监测。

（3）激励变电站选择：基于电网关键振荡模式强相关机组及变电站在各区域中的地理分布，选择通过电容器/电抗器投切可能激发强相关机组功率振荡的变电站。变电站的选择宜接近强相关机组。电气距离越近，机组对电容器/电抗器投切的响应越大，关键振荡模式越容易被激发。

（4）关键模式阻尼在线预警：对激励变电站电容器/电抗器投切SCADA（数据采集与监视控制系统）实测数据和阻尼监测机组PMU实测数据进行监测。根据SCADA记录激励变电站电容器/电抗器投切时刻，根据PMU数据搜索该时刻附近机组是否发生小幅功率振荡。对存在较为明显振荡的，记录起始振荡时刻，并对扰动后机组有功功率的动态响应轨迹进行Prony或者ARMA分析，在线获得系统关键振荡模式的频率和阻尼信息，若关键模式阻尼不足则立即预警。

3 浙江电网算例分析

浙江电网是华东电网的重要组成部分，其主要参与华东电网浙皖闽区间关键振荡模式，该振荡模式下浙江机组相对安徽和福建机组振荡。在浙江电网内部，宁波舟山地区机组对浙南机组是关键振荡模式。正常方式下，浙江电网上述2个关键模式的振荡频率和阻尼比计算结果见表1。

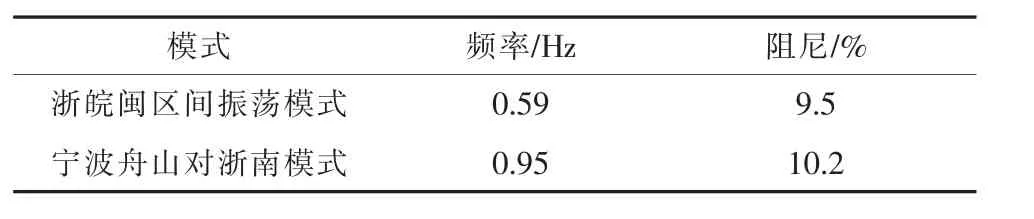
表1 浙江电网关键模式的振荡频率和阻尼

根据振荡模式参与因子计算结果，可以进一步确定重点监视机组。针对浙皖闽区间振荡模式，建议重点在浙江兰溪、安徽宣城、福建后石等电厂监视预警；针对宁波舟山机组对浙南机组振荡模式，建议重点在北仑、朗熹、温州等电厂监视预警。

图2是与安徽较近的浙北核心变电站无功投切后，近区电厂机组功率振荡仿真曲线。对图中曲线进行Prony分析可知，该扰动激发了浙皖闽区间振荡模式，振荡频率0.57 Hz，阻尼比9.7%。上述结果证明通过Prony等方法分析电容器/电抗器投切扰动冲击下强相关机组的有功功率小幅振荡实测数据，可获得电网关键振荡模式阻尼，实现低频振荡阻尼在线预警。

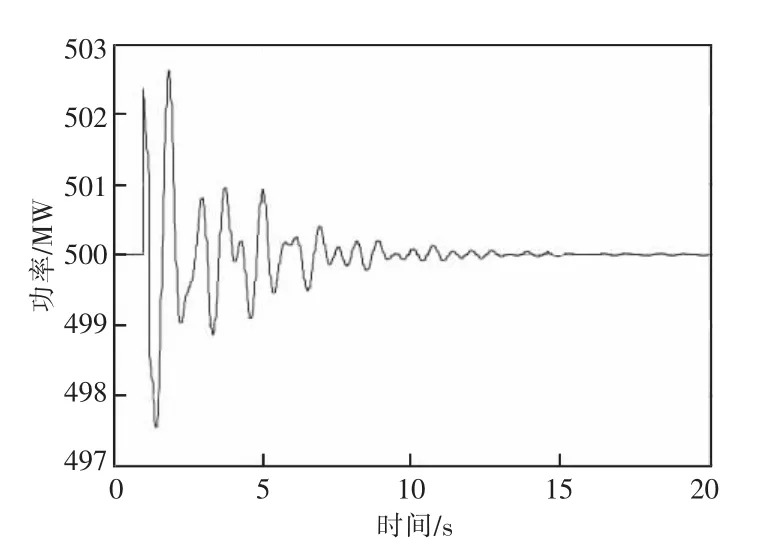
图2 浙北某变电站无功投切下近区机组有功功率曲线

4 浙江电网实例验证

以浙皖闽区间振荡模式为待监测的关键模式，浙江境内大多数机组均较明显地参与了该振荡。在实测监视预警中，选择浙江兰溪发电厂机组作为阻尼监测机组。兰溪发电厂附近金华换流站共配置17组总容量约4 900 Mvar的并联电容器和交流滤波器，而且其日常投切相对较多，故选择金华换流站作为激励变电站。

4.1 实例A

图3是金华换流站滤波器组某日SCADA实测无功功率，图中数据采样间隔为1 min。与图3滤波器组投入运行相对应时刻，实测兰溪机组PMU有功功率如图4所示，图中数据采样间隔为40 ms。由图4可见，金华换流站滤波器组无功投切的同时兰溪机组有功功率存在振荡，两者间存在因果激发关系。

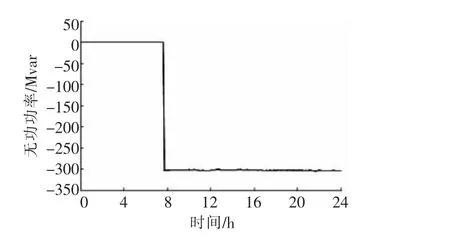
图3 金华换流站滤波器组SCADA实测无功功率

图4兰溪机组PMU实测有功功率的Prony辨识结果见表2。由表2可见，兰溪机组有功功率主要存在2个振荡模式：第1个模式是兰溪机组本机振荡模式，振荡频率1.17 Hz，阻尼比为4.42%；第2个模式是浙皖闽区间振荡模式，振荡频率0.63 Hz，阻尼比为9.11%。

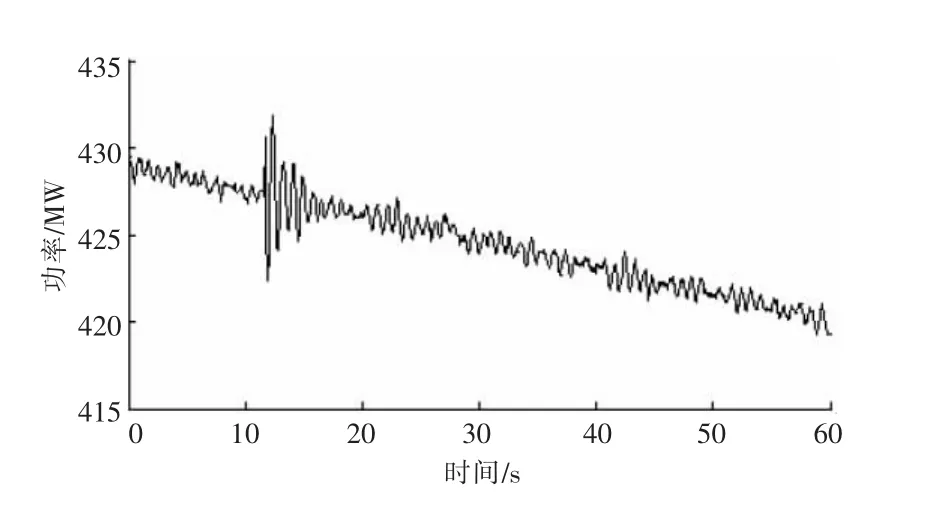
图4 兰溪发电厂机组PMU实测有功功率

表2 兰溪机组PMU实测有功功率Prony辨识结果

4.2 实例B

图5是金华换流站滤波器组另一日SCADA实测无功功率，图中数据采样间隔为1 min。与图5滤波器组投入运行相对应的时刻，实测兰溪机组PMU有功功率如图6所示，图中数据采样间隔为40 ms。由图6可见，该时段兰溪机组有功功率亦存在明显振荡，其Prony辨识结果见表3。由表3可见，与实例A类似，兰溪机组有功功率主要也存在2个振荡模式：第1个模式是兰溪机组本机振荡模式，振荡频率1.18 Hz，阻尼比为6.07%；第2个模式是浙皖闽区间振荡模式，振荡频率0.61 Hz，阻尼比为9.65%。

由前述不同时间段的2个实例分析结果可见，通过Prony等方法分析电容器/电抗器投切扰动冲击下强相关机组的有功功率小幅振荡实测数据，可获得电网关键振荡模式阻尼，实现低频振荡阻尼在线预警。

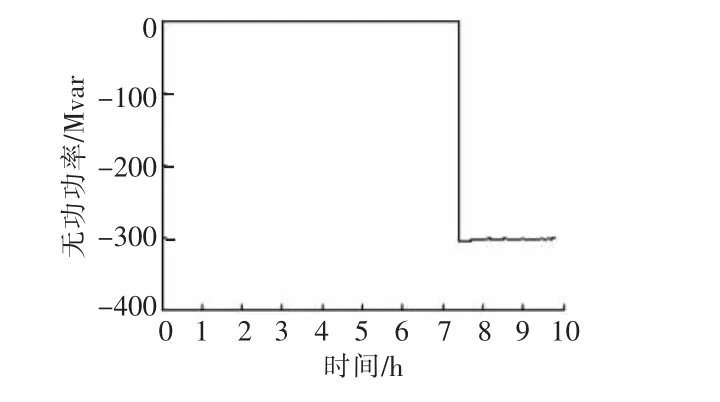
图5 金华换流站滤波器组SCADA实测无功功率

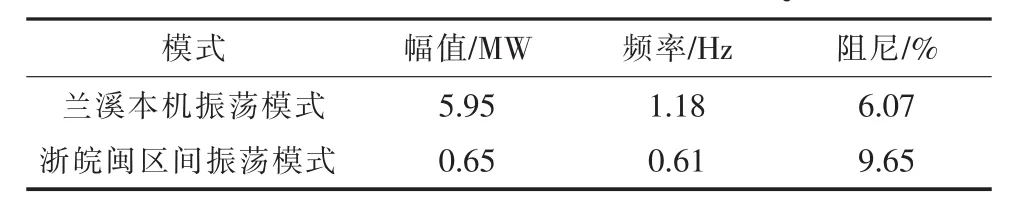
表3 兰溪机组PMU实测有功功率Prony辨识结果

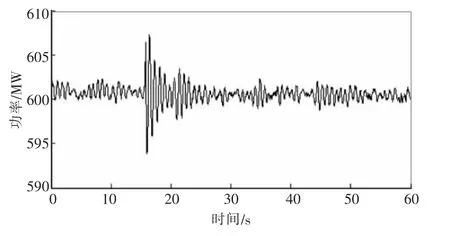
图6 兰溪发电厂机组PMU实测有功功率

5 结语

本文提出一种考虑电网日常无功投切的低频振荡阻尼在线预警方法。电网日常运行中存在大量地理分布较广、时间分布相对固定的扰动，例如大容量电容器/电抗器投切扰动具有无功功率阶跃冲击的特性，会对相邻机组造成冲击，从而激发机组参与关键振荡模式的小幅振荡。本文所提出的方法利用上述原理，通过监测变电站电容器/电抗器投切SCADA数据和关键机组PMU实测数据以辨识电网关键振荡模式阻尼。浙江电网实测数据分析结果也验证了该方法的有效性。