自适应平方根无迹粒子滤波算法及其应用
李晓明,赵长胜,张立凯
(江苏师范大学地理测绘与城乡规划学院,江苏 徐州 221116)
目前应用于GPS单点定位的非线性滤波方法有基于贝叶斯估计的各种卡尔曼滤波改进算法和贯序的蒙特卡罗方法-粒子滤波(particle filter,PF)及其结合抗差、自适应、平方根因子等的改进算法。自适应卡尔曼滤波的提出有效抑制了由于状态噪声方差和观测噪声方差的不确定而引起的滤波发散问题。基于有色噪声一阶AR模型的自适应扩展卡尔曼滤波算法确定了自适应因子,有效提升了解算过程中的收敛速度和幅度[1],缺陷在于省略了高阶项信息,而且只能在噪声较小时使用。UKF摒弃了EKF对非线性函数线性化的传统处理,对于非线性的预测方程,基于先验均值和先验方差矩阵的平方根选择采样点,对于非线性分布的统计量有较高的计算精度[2],非线性程度高时,协方差极容易出现负定,平方根无迹卡尔曼滤波具有数值稳定性,因此保证了状态协方差的正定性[3]。基于UT变换和自适应调节因子综合选取重要密度函数进行粒子的重要性重采样,提高了机器人的定位精度[4]。改进的无迹粒子滤波算法避免在状态空间进行无迹变换,从而降低了时间开销[5]。改进的非线性容积卡尔曼滤波算法在单点定位中的应用,有效地抑制了预报信息误差[6];通过将SRUKF算法和自适应因子结合,迭代计算更新系统状态方差阵和噪声方差阵的平方根,以保证系统的非负定性[7]。粒子滤波(也称为粒子云滤波)的作用主要是用于参数估计,不受高斯模型的约束,不同于UKF的是,PF借用蒙特卡洛的思想,调整离散的样本集的权值来近似后验分布,从而获得状态的最小方法估计。粒子滤波算法的定位精度适用于非线性[8]、非高斯、多维状态问题[9],能有效减弱噪声扰动,但同时增大了计算时间[10],粒子滤波过程中粒子退化问题影响了粒子滤波的应用。
本文结合无迹卡尔曼滤波、粒子滤波各自的优点,采用自适应滤波理论,提出了自适应平方根无迹粒子滤波(ASRUPF)的新算法。ASRUPF选择合适的重采样技术,分别对系统状态和观测进行更新,在保证过程噪声方差阵正定的同时,有效延缓粒子退化现象,改善了粒子滤波算法性能,提高非线性系统的状态估值精度,且具有抗差性质。应用于GPS单点定位解算中取得了较好的滤波效果。
1 自适应SRUKF算法
平方根无迹卡尔曼滤波使UT变换后的验后方差精度具有三阶精度,但滤波效果仍然受到滤波初值的影响,假设由随机变量x和具有高斯白噪声的观测变量Z构成的非线性系统描述如下
(1)
式中,xk为n维随机变量;Zk为观测值向量;f( )为系统状态函数;h( )为量测函数;状态噪声wk-1与观测噪声vk互不相关且服从高斯分布,其协方差矩阵分别为Q、R。
假设已知k-1时刻的状态均值和初始方差为Xk和P,通过UT变换得到2n+1个Sigma点集及其相应的权值,得到状态的非线性映射,过程如下。
(1) 权值计算公式为
(2)
式中,m为均值;c为协方差;λ、α、β为UT变换的参数。
(2) 采取平方根法,对权阵进行Cholesky分解,使用chol函数计算Sigma点集为
(3)
(3) Sigma点集计算及一步预测为
(4)
(5)
(4) 状态预估为
(6)
状态协方差平方根预估,采用矩阵QR分解,用状态协方差的Cholesky因子代替进行递推运算,cholupdate表示矩阵的上三角矩阵和其转置的乘积
(7)
(8)
再次使用UT变换对噪声方差的平方根进行预测为
(9)
(10)
(5) 观测预测值为
(11)
(6) 计算预测残差为
(12)
预测残差可作为预估信息准确性的评判标准,基于预测残差统计量的自适应因子可用于估计量测或状态噪声,指数函数表示的自适应因子可表示为[11]
(13)
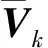
(14)
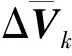
式(7) 求得观测值协方差及其与状态值的互协方差为
(15)
其中
(16)
求得滤波增益、系统的状态更新及其协方差更新为
(17)
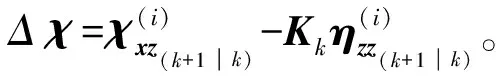
2 自适应无迹粒子滤波算法(ASRUPF)

(18)
利用粒子滤波计算采样更新粒子的核心为在一次迭代周期中UKF算法可为每个粒子计算其均值及协方差,然后用于更新采样该粒子,其实质是从建议密度函数角度来优化粒子滤波算法,从k=0时刻起,流程如下
(19)
(20)
粒子滤波算法输出的是一组样本点,当采样数量无穷大时,这些样本点可近似地表示为后验分布
(21)
状态的均值计算可表示为
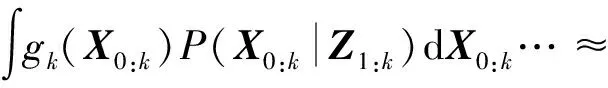
(22)
式中,gk为利益函数,若选用X0:k为边缘条件均值,此时gk(X0:k)=Xk,边缘条件均值反映了利益函数的质量。
3 ASRUPF在GPS定位解算中的应用
GPS伪距观测方程表示为[14]
ρ=R+cI+cT+cδtu-cδts
(23)
式中,ρ为伪距观测值;R为卫星与接收机的几何距离;c为真空中光速;I为电离层延迟;T为对流层延迟;δtu为接收机钟差;δts为卫星钟差。
选取的载体运动模型选择CV(常速度)模型,状态函数表示为
xk=Φ·xk-1+wk-1
(24)
其中,接收机状态
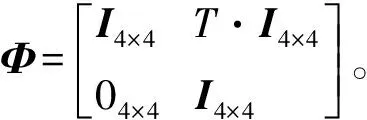
状态噪声协方差阵取为
q为位置和速度系统噪声的谱密度,取q=0.01 m2·s-3。本文算法验证所用数据为广播星历,共1364个历元,以GPS双频伪距观测消除电离层误差,采用Hop-filed模型改正对流层延迟误差[15-16],使用自适应平方根无迹粒子滤波器进行滤波处理,采用的重采样算法为残差重采样,量测噪声为
R=I(size(sat,1))
式中,sat为观测的卫星数。
初始状态协方差阵取
Qx=diag([111500111500])
以精密单点定位数据后处理值为滤波估计参考,三维位置各个方向滤波误差如图1—图3所示。
各方向位置均方误差结果见表1,一个迭代周期中各算法平均耗时见表2。
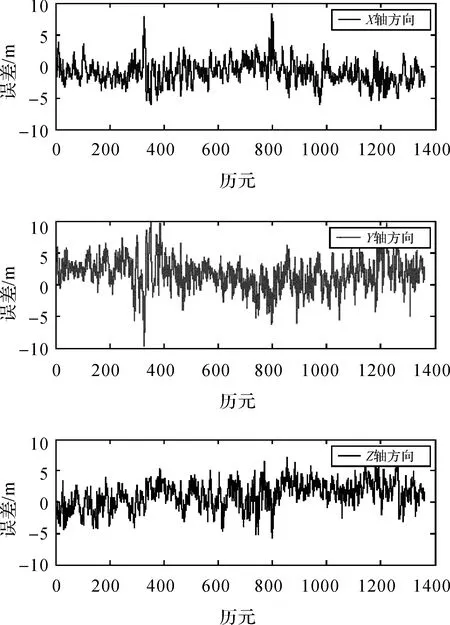
图1 LS处理结果
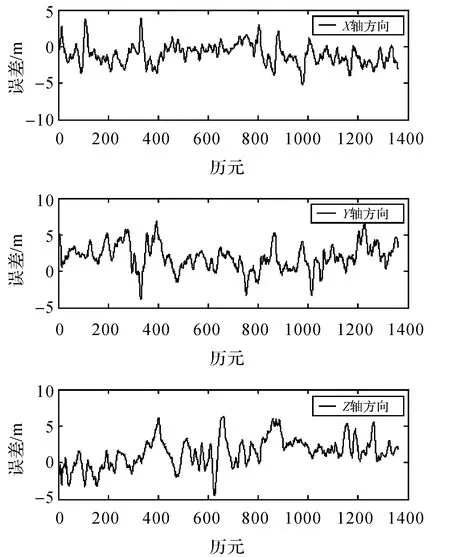
图2 ASRUKF滤波结果
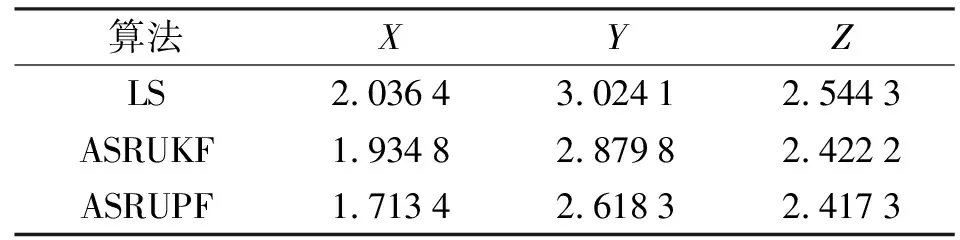
表1 三维坐标位置偏差均方根误差 m

图3 ASRUPF滤波结果

表2 各算法耗时比较 s
图1—图3的滤波结果表明,在GPS定位解算中,因UKF采用的无迹变换算法能使后验方差的精度达到三阶,UKF较LS有较高的滤波精度优势,基于预测残差统计量的自适应无迹卡尔曼滤波与粒子滤波的结合使得滤波算法得到优化,ASRUPF处理的结果相较于ASRUKF有较大的提升,自适应因子减小了误差和不确定性因素的影响,PF与UKF相比增加了粒子的多样性,延缓了退化,但是算法耗费的时间增加了,3种算法在一个迭代周期中的耗时长度LS最短,ASRUKF次之,ASRUPF耗时最长。
4 结 语
本文利用无迹卡尔曼在滤波精度上的优势,结合基于预测残差统计量的自适应因子,构建出合理的建议密度函数,从而改进了粒子滤波算法,提升了算法性能,应用到GPS定位解算领域,具有很好的定位精度,进一步提高了GPS导航定位的可靠性。目前仍然存在的问题是随着历元的增加及粒子数的增多,ASRUPF在实时性要求较高的领域相比一般的滤波算法优势不明显, 如何选择更合理的建议密度函数或更好地改进滤波算法则有待更进一步的研究。

