垂直分布数据集上的安全Skyline查询算法

吴吉斌，王箭

（南京航空航天大学计算机科学与技术学院，江苏南京211106）

Skyline查询[1]能从大量多维数据中筛选出人们感兴趣的数据，是一种重要的数据分析方法，并在推荐系统等场景中有广泛的应用。2001年，Borzsonyi等[2]研究了大规模数据集上的skyline查询算法。此后，Skyline查询在分布式存储及其相关领域受到广泛关注[3-7]。Balke等在中首次提出了垂直分布数据集上Skyline查询方案，但该方案中每个服务器只能存储一维数据，当处理多维数据时开销巨大。Trimponias等在文献[7]中提出了一种垂直划分Skyline查询算法VPS（vertical partition skyline）。该方案中每个服务器可存储任意维度的数据，降低了多维度数据集计算时的硬件开销。然而目前仅有的两种垂直分布数据集上的Skyline查询方案没有考虑数据集的隐私保护需求，查询过程中数据均以明文形式传输，服务器中存储的数据直接泄露给查询端，造成敏感数据泄露。现实生活中查询服务提供商一般为商业公司，并将其服务器内存储的数据集视为商业机密。因此如何实现垂直分布数据集上保护隐私的Skyline查询成为目前亟待解决的问题。

随着隐私保护需求的不断增长，分布式数据集上保护隐私的Skyline查询方案受到了越来越多的关注。Bothe等在[8]中提出了使用可逆矩阵加密数据并进行Skyline查询的方案。文献[9]中提出了基于0-1编码技术[10]的安全Skyline查询技术。Liu等在[11]中提出了一种基于使用Paillier算法[12]加密的双服务器Skyline查询方案。然而，以上方案在数据比较过程中，服务器均需拥有数据点的所有维度，因此不适用于垂直划分数据集上的Skyline查询。本文提出了垂直分布式的保护隐私Skyline查询方案PPVPS。该方案使用安全多方和积协议对不同参与方之间的交互数据加密，实现待查询数据集的隐私保护，并能实现抗合谋攻击。最后通过理论分析证明了该方案的安全性，并通过模拟实验对协议运行效率进行了评估。

1 预备知识

1.1 Skyline查询

Skyline查询是一种数据分析方式，是指从给定d维度数据集DS中，选出子集S，其中子集S中的所有数据点不被任意其他数据点支配。这里支配是指对于d维数据点P和Q，如果数据点P每个维度都不比数据点Q差，并且数据点P至少有一个维度上比数据点Q好，那么就称数据点P支配数据点Q。这里假设数据点每个维度上的较小值优于较大值，比如对顾客而言，商品价格越低越优。对于给定数据集DS中的数据点P，若数据点P支配该数据集内较多的数据点，则称该数据点为锚点，记做Panc。

定义1（帕累托一致函数）对任意函数f，如果向量 P1支配向量 P2，一定存在 f（P1）f（P2），则称函数 f为帕累托一致函数。

这里通过一个例子介绍skyline查询在推荐系统中的应用。假设某旅客要去海边旅游，需要订一个价格便宜并且离海边近的酒店。某旅游公司的数据库中存储了各个酒店的价格和到海边的距离，如图1所示，以每个点表示一个酒店，其中x轴表示酒店价格，y轴表示酒店到海边的距离。对于图中的酒店A和酒店B，酒店A的价格和到海岸的距离都小于酒店B，因此酒店A支配酒店B。图中不存在某酒店价格和到海岸的距离均小于酒店A，因此酒店A不被任何其他酒店支配，酒店A是Skyline点。可以看出虚线相连的4个点是这些酒店中的Skyline点。

图1 Skyline查询经典案例

假设 d 维数据集 DS={P1，P2，…，Pn}垂直分布在m个服务器中。这里以m为2举例，数据垂直分布方式如图2所示，服务器N1和N2分别存储数据点不同维度，并且除数据点的ID外，两服务器存储维度不重复。

图2 垂直分布示意图

1.2 VPS算法

2013年，Trimponias等[7]提出了一种垂直分布数据集上的Skyline查询算法VPS。假设d维数据集 DS={P1，P2，…，Pn}垂直分布在 m 个服务器中，则数据点Pi的维度和为：

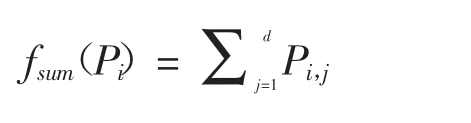
假设数据点P在服务器Ni中的投影为P.Di，则数据点P在服务器Ni中的维度和为fsum（P.Di）。服务器按fsum从小到大顺序排列数据点，查询端Client初始化Panc为空，该算法执行过程如下。

1）选择未返回Panc的服务器Ni，发送Ni序列顶端数据点P到查询端

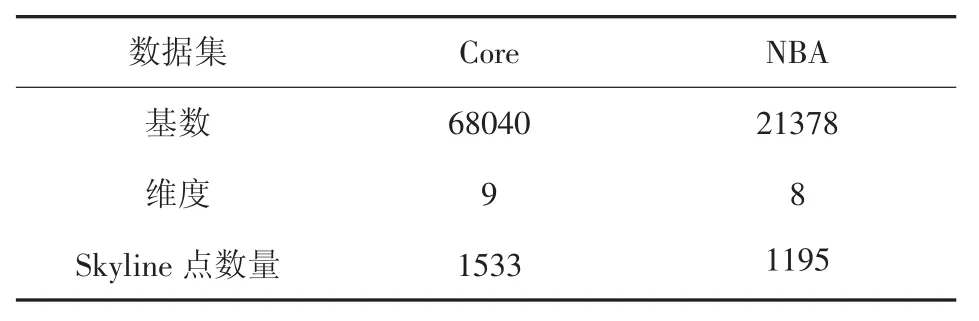
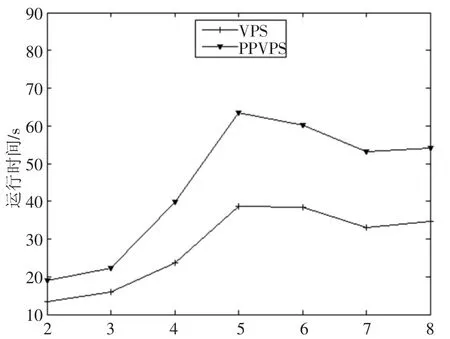
2）若数据点P与Panc的维度和满足fsum（P）

3）重复1-2，直到所有服务器返回Panc。

4）所有服务器计算Panc的本地支配区间，将不被Panc支配的数据点发送到查询端

5）查询端在剩余数据点上计算Skyline

文献[7]给出了该算法详细的正确性分析和准确性证明。但该算法中数据以明文形式传输，服务器存储的数据直接泄露给查询端，无法满足用户隐私保护需求。

1.3 安全多方和积协议

Yang等在文献[13]中提出了一种抗合谋攻击的安全多方和积协议SPOS（Secure Product of Summations Protocol），该协议使用同态加密[12]实现安全多方和积的计算，并能够抵抗合谋攻击。该协议假设有m个参与方且第i个参与方Ni有数据（xi，r）i，m方合作计算并保证计算过程中任意参与方无法获得其他参与方的任何有效数据。该协议中参与方是平等的，在计算过程中每个参与方执行相同的操作，不存在中间节点。

文献[13]中对该协议的安全性进行了详细的证明。在半诚实模型下，该协议是（m-1）-隐私[14]的，即前m-1个参与方共谋，也无法推测出第m个参与方的有效数据。

2 隐私保护的垂直划分skyline查询

本节介绍隐私保护的垂直划分Skyline查询协议（PPVPS），该协议能实现垂直划分数据集上的安全Skyline查询。

2.1 系统模型

图3 系统模型

如图3所示，该系统模型包括一个客户端（Client）和 m（m>1）个服务器{N1，N2，…，Nm}。包含 n 个 d 维数据点的数据集 DS={P1，P2，…，Pn}垂直分布在m个服务器中。假设集合Di中不存在完全相同的两个点，即任意两个点Pa.Di=（Pai1，Pai2，…，Paik）和 Pb=（Pbi1，Pbi2，…，Pbik），至少存在一个正整数 j∈[1，k]，满足 Paij≠Pbij。客户端的目标是从数据集DS中查找出所有的skyline点。由于每个子数据集包含了隐私信息，每个服务器所持有的子数据集既不愿意发送给其他的服务器，也不愿意泄漏给客户端。

2.2 PPVPS协议

该协议可以分为三个部分：第一部分筛选锚点，第二部分筛选出不被锚点支配的数据点，第三部分在筛选出的数据上计算skyline。

第一部分（步骤1-6）服务器先对数据进行预处理，按照fsum值从小到大的顺序生成序列Li。客户端选择一个未返回当前锚点的服务器，返回该服务器序列顶端的数据点P的ID。其中数据点P不能属于序列VS，否则重新返回下一个数据点。如果Panc为空，则令Panc=P，否则客户端将数据点P和锚点Panc的ID发送给所有服务器。

对于服务器Ni，该服务器计算fsum（Panc.Di）和fsum（P.Di）的值，并令xi=fsum（Panc.Di）-fsum（P.Di），并生成随机正整数ri。根据SPOS，客户端生成p，其中p=因为所以若p>0，可得 fsum（Panc）-fsum（P）>0，即 fsum（P）0，则令Panc=P。重复步骤2-5直至所有服务器返回当前锚点。

第二部分（步骤7）服务器返回不被锚点支配的数据点的ID。若该数据点未在第一部分中返回客户端，则客户端将该数据点插入序列VS尾部。值得注意的是，第一部分和第二部分中数据点按服务器序列顺序返回，因此序列VS中排在前面的数据点一定不被排在后面的数据点支配。假设序列VS中排在前面的数据点P1被排在后面的数据点P2支配，因此任意服务器Ni中P2至少有一个维度小于P1，因此在Ni中P2的各维度值之和一定小于P1的各维度值之和，即满足fsum（P2.Di）

第三部分（步骤8-12）是在序列VS的数据上计算SKY。客户端选取序列VS前端的数据点P和集合SKY中的数据点P*，如果SKY为空，则将数据点P放入集合SKY。否则客户端将数据点P和数据点P*的ID发送到服务器。

协议隐私保护的垂直划分skyline查询算法（PPVPS）输入：服务器输入数据集DS输出：客户端输出SKY 1．客户端初始化 Panc= φ，VS= φ 2．客户端选定任意未返回当前锚点的服务器Ni，并按顺序返回序列Li顶端数据P（P∈VS）的ID，并将P存入序列VS 3．若Panc=φ，则令Panc=P，否则将P和Panc的ID发送到所有服务器4．任意服务器Ni计算xi=fsum（Panc.Di）-fsum（P.Di）5．客户端计算p=SPOS（xi，ri），i=1，2，…，m。如果p>0则令Panc=P 6．重复步骤2-5直到所有服务器返回当前锚点7．任意服务器Ni将所有不被锚点本地支配的数据P的ID返回客户端，如果P∈VS，将P插入序列VS尾部8．客户端初始化SKY=φ 9．客户端按顺序选取VS顶端元素P，若SKY=φ，则将数据点P加入集合SKY，否则选取SKY集合内任意数据P*，并将P和P*的ID发送到所有服务器10．对于服务器 Ni，如果 P*.Di支配 P.Di，则服务器 Ni令 xi=0，否则令 xi=random（0，1）11．客户端计算p=（xi，ri），i=1，2，…，m。若对于任意P*都有p≠0，则将P加入集合SKY 12．重复9-11直到序列VS内所有元素被选取，输出SKY

对于任意服务器Ni，如果P*.Di本地支配P.Di，则令xi=0，否则令xi为正随机数，并生成随机正整数ri。随后根据SPOS，客户端生成因为不等式0恒成立，所以若p≠0则≠0，即数据点P不被数据点P*全局支配。如果数据点P不被集合SKY内任意数据点支配，则将数据点P是Skyline点，并将其放入集合SKY。重复步骤9-11直至序列VS内的所有数据点被选取。协议完成后，集合SKY是最终筛选出的Skyline点集合。

3 协议分析

3.1 正确性分析

定理1 在半诚实模型下，本文所提出的PPVPS能够正确地计算出所有的Skyline点。

证明：证明可以分为两点，第二部分执行完毕后所有的Skyline点都被返回客户端；第三部分中只需判断后选中的数据点是否被SKY集合内的数据点支配，即可确定该数据点是否为Skyline点。第一点：假设某Skyline点P未返回客户端，因为该点是Skyline点，所以点P某维度一定优于锚点，则该点在某服务器内不被锚点支配。服务器会将不被锚点支配的数据点返回客户端，因此该点在第二部分完成时一定已被返回客户端。第二点：第三部分客户端按fsum从小到大的顺序对数据点排序，fsum是帕累托一致函数，因此序列前端的数据点一定不被序列后端的数据点支配，因此只需要判断后选中的数据点是否被SKY集合内的数据点支配。

3.2 安全性分析

定理2 （[15]）假设g可以安全约减成f，并且f是安全的，那么一定存在一个协议安全的计算g。

文献[15]中Goldreich提出安全性约减理论，该理论提出如果一个协议能够使用f安全的计算g，则称g可安全约减成f。

定理3 在半诚实模型下，本文提出的PPVPS能是（m-1）-隐私的，可以抵抗合谋攻击。

证明：PPVPS协议的数据交互有两类：客户端和服务器间传输的数据点ID和调用协议SPOS的输入和输出。显然参与方无法通过数据点ID推导出相关隐私信息，并且协议SPOS是（m-1）-隐私的，PPVPS协议可安全约减为协议SPOS，因此PPVPS协议是（m-1）-隐私的，可以抵抗合谋攻击。

4 实验评估

本实验以多台 Ubuntu 12.04，3.40GHz CPU，8GB RAM的台式机模拟服务器，以一台Windows7，2.20GHz CPU，8GB RAM的台式机模拟查询端。实验数据集采用的是skyline查询经典数据集Core和NBA。其中数据集Core含有68K条9维数据记录，共有1533个skyline点。数据集NBA含有21K条8维数据记录，共有1195个skyline点，数据集的相关信息如表1所示。

表1 数据集信息

该实验过程利用Socket实现服务器与查询端之间的数据通信。本实验结果受到待测试数据集基数和服务器数量的影响，并且不同数据集锚点分布不同，会对实验结果造成一定的影响。图4展示了在Core数据集中，PP-VPS协议和VPS协议在服务器数量从2增长到9的过程中的计算时间。当服务器数量从2增长到5时，PPVPS协议运行时间从65.849秒增加到200.945秒。当服务器数量小于5时，PPVPS和VPS算法执行时间近似，当服务器数量大于5时，PPVPS执行时间出现较快增长。

图4 Core实验结果对比

图5展示了在NBA数据集中，PPVPS协议和VPS协议在服务器数量从2增长到8的过程中的计算时间变化曲线。从图中可以看出，随着服务器数量从2增加到5，协议运行时间从19.013 s增加到63.354 s，当服务器数量逐渐增加到8时，VPS协议和PPVPS协议的计算时间出现波动，这是因为数据集的分布影响锚点筛选，从而影响协议运行时间。

图5 NBA实验结果对比

当服务器数量较少时，PPVPS协议在实现安全Skyline查询的条件下，计算时间与VPS协议近似，该实验证明了PPVPS协议的可行性。

5 结束语

提出了一种垂直分布数据集上保护隐私的Skyline查询协议。理论分析显示本方案能够正确地实现Skyline查询，并保护数据集的隐私信息。在参与者合谋攻击的情况下，依然可以确保隐私信息的安全。进一步，还通过理论分析和模拟实验对新协议的运行效率进行了评估，结果显示可以取得较高的运行效率。在未来的工作中，将着重研究协议效率的提升和通信复杂度的降低，使其在现实中得到广泛的应用。