基于IWRAP模型的船舶交通流数据拟合模型

柯冉绚， 胡栩祯， 陈 毅

(集美大学 航海学院，福建 厦门 361021)

伴随船舶大型化、交通流密集化等问题，航道的风险管理日趋重要，科学的管理是保障船舶安全行驶的有效途径。[1]在船舶交通流统计的基础上，使用IWRAP模型计算水域的船舶碰撞和搁浅的概率，对于了解水域的安全情况具有重要意义。[2]

吴兆麟[3]采用港口或选定水域的交通流数据，将对某一特定时期内(如季度或年度)所发生的船舶交通事故数量与该期间内船舶活动量的比值作为衡量该港口或水域在该期间内的船舶交通安全状况的指标。孙苗等[4]根据水域辖区内的交通流情况，提出利用船舶交通服务(Vessel Traffic Service, VTS)系统设置船舶可能存在的搁浅判定条件，指导相关人员及时向存在搁浅风险的船舶发出预警信息，及时提醒船舶人员采取应对措施。黄纯等[5]借助长江口水域2010—2015年的交通流数据，实际数据发生船舶碰撞事故为21.8起/a，搁浅事故频率平均为1.8起/a；使用IWRAP MKII软件的计算结果是碰撞事故平均为21.05起/a，搁浅事故频率平均为2.298起/a，计算结果与实际情况比较相符。

已有的研究较少涉及安全评价的定量分析；另外，已有的定量研究在使用IWRAP MKII软件时，主要关注模型运行结果与实际是否相符，本文则侧重于以交通流分布函数的拟合度，即选择数据的分布函数这个起源，探究模型运行结果的可靠性，提出模型拟合优化的方法，提供更好应用IWRAP MKII软件分析水域风险的思路。

1 IWRAP模型基础理论

加拿大海岸警卫队和丹麦科技大学联合开发的航道风险评估工具IWRAP(IALA Waterway Risk Assessment Program)是一种以事故致因概率为前提， 基于船舶自动识别系统(Automatic Identification System, AIS)历史数据对船舶碰撞和搁浅概率进行理论计算的模型，它可以有效地对在不同航段中的不同类型的船舶碰撞和搁浅的概率进行计算和分析比较，并进行预测。

1.1 潜在碰撞船舶数量计算模型

碰撞可以简单地分为两种类型：发生在直线航段碰撞，即对遇碰撞和追越碰撞；发生在交叉航段的碰撞，即交叉碰撞。针对两种不同的碰撞方式，该模型运用不同的计算方法。

1.1.1直线航段计算模型

在直线双向航道上，沿航线航行的船舶发生几何碰撞事故的潜在船舶数量为

(1)

(2)

若f(yi)(1)和f(yj)(2)都是正态分布，且其分布参数分别为(μi,σi)和(μj,σj)，则对遇潜在碰撞船舶数量的计算式可简化为

(3)

(4)

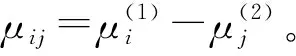
1.1.2弯曲航段计算模型

IWRAP模型中，将两船夹角为 10°～170°时定义为交叉相遇，两船在交叉相遇的过程中发生碰撞的情形见图2。在交叉航道上，船舶发生几何碰撞事故的潜在船舶数量可表示为

(5)

1.2 潜在搁浅船舶数量计算模型

搁浅分为操纵性搁浅和漂移性搁浅两类。操纵性搁浅是由于人为错误或者船员缺乏警惕性造成的(第I类)；漂移性搁浅是由于操作或者推进装置失效，船舶失去自航能力造成的(第II类)。水域内的预计搁浅事件或与固定物体碰撞的预计次数的模型见图3。

根据模型，上述搁浅类别中预计搁浅事件数量为

(6)

(7)

式(6)和式(7)中：ai为导航器进行2次定位的平均距离；d为导航路线中从障碍物到航线转弯的距离，随着船舶的横向位置s而变化；i为船舶种类，按船舶类型和自重或长度分类;fi(z)为船舶交通的概率密度函数；NI为预计每年I类搁浅事件的数量；NII为每年预计第II类基准事件的数量；Pc,i为因果概率，即在搁浅过程中船舶搁浅和船舶之间的比率；Qi为第i级船舶每年通过路线横断面的数量；Z为垂直于航道方向的坐标；Zmin，Zmax分别为障碍物的横向坐标。[6]

2 风险建模与评估流程

2.1 风险的基本概念和量化方法

指定海域中通航的船舶交通风险，该风险显示为此航线上通行的船舶发生碰撞或搁浅的概率，并量化为某个指定的时间段内发生该事故数。

通过对指定航线上航行的船舶进行碰撞和搁浅频率的评估进行风险的量化。首先确定航线和水域，之后导入相关的AIS数据，分析该水域的交通流分布函数，与IWRAP MKII软件中提供的7种交通流分布函数进行拟合，经分析和比较，选择最符合实际数据的拟合曲线，然后在IWRAP MKII软件中运行，计算该水域所有船舶碰撞和搁浅的概率，且进行验证，从而提高应用该模型算法计算船舶碰撞概率的准确度，为选定的水域内船舶风险评估提供参考。

2.2 IWRAP MKII简介

IWRAP MKII应用程序是为用户提供一个评估指定水域内船舶碰撞和搁浅风险的量化工具。IWRAP MKII允许设置不同的场景，评估因交通流量和交通流的组成发生变化，或者航道几何结构变化，或者助导航设施的变化，或者其他缓解风险的选项也变化的情况下，碰撞和搁浅年平均数量(概率)产生的变化。IWRAP MKII是基于MS-WindowsTM的应用程序实施的，其风险评估流程涉及以下步骤[7-8]：

1) 定义水深、航线、航点和航段。

2) 在每条航道输入交通流分布。

3) 定义每条航段的船舶统计分布。

4) 标识漂移引起的搁浅。

5) 定义该地区的其他交通。

6) 选择概率影响因素。

7) 结果计算和评估。

使用厦门港2016年的AIS数据进行拟合，并运行IWRAP MKII软件，进行数据分布函数拟合的分析和比较，以此说明分布函数拟合度越好，该软件运行的结果与实际风险情况的相似度越高。

3 厦门港交通流数据的统计分析

3.1 厦门港的进港和出港数据图示分析

本文使用的交通流数据来自2016年厦门港主航道内进出港集装箱船舶的VTS截面数据基础上预处理过的数据。数据的处理是在定义航段基础上进行的，所定义的航段在厦门港九节礁附近的主航道上，该航段交通流较为密集，是船舶进出厦门港的必经之路。

根据厦门港2016年的集装箱船交通流数据，将交通流数据分为进港和出港两部分，在EXCEL中画出直方图，结果见图4和图5。从图4和图5可知：厦门港进出港的交通流分布呈先上升再下降的趋势，与IWRAP MKII软件中的7种曲线—Normal(正态分布)曲线、Gumbel(max)(极大值)曲线、Gumbel(min)(极小值)曲线、Lognormal(对数正态分布)曲线、Uniform(均匀分布)曲线、Weibull(韦伯分布)曲线、Beta(贝塔分布)曲线对比而言：7种曲线中，Uniform(均匀分布)函数呈水平直线趋势，其余6种分布函数曲线均呈先上升后下降趋势。图4和图5的分布图表明厦门港集装箱船进出港的分布并非Uniform(均匀分布)。因此，初步的分析中，先把Uniform(均匀分布)曲线排除，然后将实际数据与其余6种曲线的分布进行比对。

3.2 交通流数据与各曲线的相关性

3.2.1 相关系数简介

相关系数是反映变量之间关系密切程度的统计指标，按积差方法计算，以两变量与各自平均值的离差为基础，以两个离差相乘来体现两变量之间的相关程度。

相关系数一般用字母r表示，度量两个变量间的线性关系，其定义式为

(8)

式(8)中：Cov(X,Y)为X与Y的协方差；Var[X]为X的方差；Var[Y]为Y的方差。

相关系数表示X和Y之间线性关系的紧密程度，定量体现X和Y的相关程度，即相关系数越大，相关程度越大。相关系数等于0表示相关程度最低，通常认为X和Y不存在线性关系。需要注意相关系数的正负号只表示相关的方向，绝对值为相关的程度。利用相关系数的性质计算厦门港交通流数据分布和各分布函数的相关系数并进行对比，筛选与厦门港实际交通流数据分布最接近的函数曲线。

3.2.2 厦门港进港船舶数据

在MATLAB软件中使用corrcoef函数计算两个序列的相关度，corrcoef(x，y)表示序列x和序列y的相关系数，得到的结果是一个2×2矩阵，其中对角线上的元素分别表示x和y的自相关，非对角线上的元素分别表示x与y的相关系数和y与x的相关系数，两者相等。

使用corrcoef函数时，两个序列的元素个数应相同。先设定一个随机数列，然后用corrcoef(x，y)得出两数列的相关系数。

将厦门港进港船舶数据导进MATLAB软件，进行这些数据的分布与IWRAP MKII中6个分布函数的相关系数计算。

1)与Normal(正态分布)函数相关系数的计算。生成3 180×1的正态分布矩阵数据，以z=corrcoef(A,B)指令计算相关系数，zNormal=0.008 9。

2)与Weibull(韦伯分布)函数相关系数的计算。生成3 180×1的韦伯分布随机矩阵数据，然后以z=corrcoef(A,C)指令计算相关系数，zWeibull=0.002 1。

3)与Lognormal(对数正态分布)函数相关系数的计算。生成3 180×1的对数正态分布随机矩阵数据，然后以z=corrcoef(A,D)指令计算相关系数，zLognormal=0.003 1。

4)与Beta(贝塔分布)函数相关系数的计算。生成3 180×1的Beta(贝塔分布)随机矩阵数据，然后以z=corrcoef(A,E)指令计算相关系数，zBeta=-0.004 3。

5)与Gumbel(max)(极大值)函数相关系数的计算。生成3 180×1的Gumbel(max)(极大值)函数随机矩阵数据，然后以z=corrcoef(A,F)指令计算相关系数，zGumbel(max)=-0.007 7。

6)与Gumbel(min)(极小值)函数相关系数的计算。生成3 180×1的Gumbel(min)(极小值)函数随机矩阵数据，然后以z=corrcoef(A,G)指令计算相关系数，zGumbel(min)=-0.003 3。

比较以上相关系数的绝对值，可知zNormal>zGumbel(max)>zBeta>zGumbel(min)>zLognormal>zWeibull，6个函数中，厦门港的进港集装箱船舶分布与Normal(正态分布)函数相关程度最高，故之后将采用正态分布函数来表示2016年厦门港的进港集装箱船舶数据分布。

3.2.3 厦门港出港船舶数据

出港数据与进港数据计算过程类似。首先将厦门港出港船舶数据导进MATLAB软件，在MATLAB软件中进行计算，形成一个3 188×1的矩阵，得出以下结果。

1)与Normal(正态分布)函数相关系数为zNormal=-0.005 2。

2)与Weibull(韦伯分布)函数相关系数为zWeibull=0.007 2。

3)与Lognormal(对数正态分布)函数相关系数为zLognormal=0.009 8。

4)与Beta(贝塔分布)函数相关系数为zBeta=0.001 1。

5)与Gumbel(max)(极大值)函数相关系数为zGumbelmax=0.005 6。

6)与Gumbel(min)(极小值)函数相关系数为zGumbelmin=0.002 3。

通过对比上述相关系数的绝对值结果，可知zLognormal>zWeibull>zNormal>zGumbelmax>zBeta，即在6个函数中，厦门港出港集装箱船舶的分布与Lognormal(对数正态分布)函数相关程度最高。以上可见，进出港数据拟合分别匹配不同的分布函数，这也是在使用IWRAP MKII模型时需要留意的。

4 实例应用与验证

通过IWRAP MKII软件计算出厦门港2016年碰撞事故数并与实际发生的碰撞事故数进行对比，其差值越小，代表越接近实际情况，验证选择的交通流数据的分布函数曲线与实际交通流数据分布的拟合程度越高，使用IWRAP MKII计算船舶碰撞和搁浅的次数与实际更相符，即软件评估风险的准确性越高。

4.1 厦门港主航道地形数据建模

地形数据建模包括构建出海图上出现的岛屿、暗礁和陆地等，必须使用IWRAP MKII软件自带的多边形工具手动构建。根据软件中的Google地图并结合厦门港九节礁附近的主航道海图建模见图6。

4.2 交通流分布建模

关于岛屿、暗礁、浅滩、陆地等构建完成后开始设置交通流信息。从上述结果可知，进港方向数据最接近Normal(正态分布)函数，出港方向最接近Lognormal(对数正态分布)函数。验算分两部分：第1部分在东向(进港)的数据设置上选择Normal(正态分布)曲线，在西向(出港)上分别选择不同的曲线Normal(正态分布)曲线、Gumbel(max)(极大值)曲线、Gumbel(min)(极小值)曲线、Lognormal(对数正态分布)曲线、Weibull(韦伯分布)曲线、Beta(贝塔分布)曲线完成计算；第2部分在西向(出港)的数据设置上一直保持选择Lognormal(对数正态分布)曲线，在东向(进港)上选择不同的曲线完成计算，以达到单一变量的效果，确保验算的一致性。交通流分布设置界面部分截图见图7。

航段内交通流量是根据交通流量分布编辑器进行设置的。交通流量分布编辑器主要设置航段内每年船舶航行的数量、船舶的类型和船舶航行速度等相关设置。

IWRAP MKⅡ软件默认在原油油船、成品油油船、化学品船、天然气船、集装箱船、杂货船、散货船、滚装船、客船、快速渡船、支持船、渔船、油船、其他船对这14种船型进行区分，每种船型按25 m间隔分为若干个长度类别，分别为0～25 m，25～50 m，…，400 m及以上。此次计算的基础数据为集装箱船舶数据，填入集装箱船的交通流量分布即可。

厦门港进港方向集装箱船舶分布统计见图8，厦门港出港方向集装箱船舶分布统计见图9。设置完成后，由MATLAB软件运行进行计算。

4.3 评估结果分析与验证

基本参数设置完成后，计算结果见图10，东向(出港)数据设置保持不变，6种曲线对应的碰撞事故分析结果如图10所示。

从图10可看出：选择Beta(贝塔分布)曲线计算结果为1.568起/a、选择Weibull(韦伯分布)曲线计算结果为1.806起/a、选择Lognormal(对数正态分布)曲线计算结果为1.933起/a、选择Gumbel(min)(极小值)曲线计算结果为1.553起/a、选择Gumbel(max)(极小值)曲线计算结果为1.709起/a、选择Normal(正态分布)曲线的计算结果为1.648起/a，已知实际上2016年的碰撞事故6起，计算与实际碰撞事故数的差值并比较可以得出，选择运用Lognormal(对数正态分布)曲线所进行的运算结果与实际最为接近。

同理，在西向(出港)数据设置不变情况下，6种分布曲线对应的计算结果为：选择Beta(贝塔分布)曲线计算结果为1.683起/a、选择Weibull(韦伯分布)曲线计算结果为1.234起/a、选择Lognormal(对数正态分布)曲线计算结果为1.318起/a、选择Gumbel(min)(极小值)曲线的计算结果为1.525起/a、选择Gumbel(max)(极小值)曲线计算结果为1.745起/a、选择Normal(正态分布)曲线计算结果为2.032起/a，已知实际上2016年的碰撞事故6起，计算与实际碰撞事故数的差值并比较可得出，选择运用Normal(正态分布)曲线所进行的运算结果与实际最为接近。

统计学理论认为交通流分布数据服从正态分布函数，但是本范例通过厦门港2016年的数据分析后认为，实际上船舶航迹分布不是典型的正态分布函数，因此，应先进行交通流分布函数的拟合，选择最为接近的分布函数。函数的选择影响建模后的运行结果与实际结果的差距，函数越接近实际数据的分布增加，建模的差距就越小，计算结果也就越接近实际情况。

5 结束语

定量型航道风险评估工具IWRAP是IALA(The International Association of Marine Aids to Navigation and Lighthouse Authorities)推荐使用的航道风险管理工具。本文关注IWRAP模型中的交通流数据建模，建模过程中需要输入船舶交通流分布，通过计算、对比与分析发现，从AIS导出的船舶交通流数据，部分接近正态分布函数，部分非正态分布，而现有的一些研究基本将其归为正态分布。IWRAP MKII软件运算结果显示，分布函数拟合的相关系数越大，得出的风险预测结果就越接近实际。因此，在运用IWRAP MKII软件的时候，应根据具体的交通流数据先进行分析对比，选择拟合度较好的分布函数，从而更有效地发挥IWRAP模型的作用。

囿于基础数据是AIS导出的数据，实际上可能存在AIS数据缺失或屏蔽AIS信息的船舶，以及不规则交通流的影响等，本文在分析和比较分布函数的选择对于IWRAP模型运算结果的影响时，设置单一变量，从而避免其他因素的影响，因此即便IWRAP MKII软件验证过程中得到的碰撞结果与实际值存在差异，但并不影响拟合函数对比分析的可行性。后续研究可以增加水域内多个航段的设置，以及多种船型的配置，多角度地进行拟合分布曲线与IWRAP MKII运行结果的影响分析，让本文的论点更具普适性，也更好地完善IWRAP MKII进行风险评估的适用性。