卫星回收舱再入过渡流区气动热数值计算

贾居红 胡丽杰



卫星回收舱再入过渡流区气动热数值计算

贾居红1胡丽杰2

（1 海军91267部队，福州 350015）（2 中国人民大学信息学院，北京 100872）

返回式卫星进入地球大气层95km高度左右时，速度达到>20，回收舱被高超声速稀薄来流形成的弓形激波环绕，气动加热问题非常明显，准确预测过渡流区的气动热成为一个十分突出的问题。过渡区由于气体空气分子仍然比较密集，基于分子动力学的直接蒙特卡洛模拟方法（DSMC）极其耗费计算资源，而求解Navier-Stokes（N-S）方程的方法误差较大。采用添加二阶滑移条件的N-S方程求解过渡流区气动热，并与开源DSMC2V程序计算结果对比，研究了舱体母线热流、压强系数变化；通过对比两种方法下舱体前缘弓形激波及流场参数变化，分析了滑移条件影响壁面和流场参数的机理。结果表明：回收舱再入过渡区时，钝头驻点区为高压、高热流区，锥身区气动热和壁面压强保持在较低水平。带滑移条件的计算机流体力学方法（Computational Fluid Dynamics，CFD）计算得到的热流、压强系数与DSMC结果吻合良好，具有计算效率高、精度较高的优势。对流场压力、温度、速度等参数分析显示，滑移条件中壁面速度滑移和温度跳跃的加入，改变了壁面流动参数，进而改善了壁面热流和压强的准确模拟能力。滑移条件对外流场参数的影响极小，没有改善稀薄流区流场的模拟能力和激波捕获能力，模拟得到的温度、速度等流场参数及激波位置、激波层厚度等与DSMC结果仍有差别。可以认为，文章采用方法能够满足工程上快速高效预测卫星回收舱再入过渡流区气动热需要。

高超声速 气动热 回收舱 计算流体力学 滑移条件 返回式卫星

0 引言

返回式卫星主要用于遥感和空间科学实验，具有显著的经济和社会效益。其微重力条件可以达到10–5n甚至更高的水平，这是载人飞船与航天飞机无法比拟的[1-3]。近年来，返回式卫星由于其优越的微重力环境和低成本，而在空间科学试验领域受到各国青睐，最具代表的是俄罗斯和欧空局的“光子”号和“生物”号系列空间科学实验卫星。

卫星完成在轨任务后，经过制动减速返回地球，再入过程中速度达>20，高超声速来流形成弓形激波包裹在卫星周围，流场温度接近2 000K[4]。除了来流空气与卫星舱体摩擦生热之外，高温条件下空气发生化学反应、返回舱体表面材料催化特性也会给返回舱壁面热载荷带来影响[5-6]，准确预测再入过程气动热是回收舱再入需要解决的难题之一。地面预测高超声速气动热的方法主要有风洞试验、数值模拟和工程预估，由于稀薄空气高超声速气动热风洞试验难度较大且费用高昂，工程预估精度难于保证，采用数值方法预测再入过程气动加热成为一种经济高效的选择[7]。目前，数值模拟高超声速气动热的方法主要有基于分子动力学的直接蒙特卡洛模拟法（DSMC）[8-9]和求解Navier-Stoke（N-S）方程的计算机流体力学方法（CFD）。空气的稀薄程度通常用克努森数来表征[10]，定义为分子平均自由程与流动特征尺度的比值。对于连续流区（<0.001），带滑移条件的计算机流体力学方法（Computational Fluid Dynamics，CFD）方法能具有较高气动热预测精度；对于自由分子流区（>10），DSMC方法是不二之选；对于过渡流区（0.1<<10）而言，由于气体分子比较密集，DSMC方法极其耗费计算资源，而基于连续性假设的N-S方程方法误差过大。因此，添加滑移条件的N-S方程方法成为一种折中选择[11-12]。本文以DSMC方法为对照，采用添加滑移条件的N-S方程求解过渡流区小型再入卫星表面气动热，为工程上多工况快速预测提供借鉴。

1 几何模型与来流条件

卫星返回舱外形如图1（a），前部为回收舱，后部为制动舱。回收舱体布局为球锥结构形式[13]，球头半径为0.267 8m，后体半锥角11.4°，底部半径0.503 5m，舱体总长1.41m，详细参数如图1（b）所示。图1中以返回舱头部顶点为坐标原点，横坐标为舱体轴向距离,纵坐标为舱体切向距离。

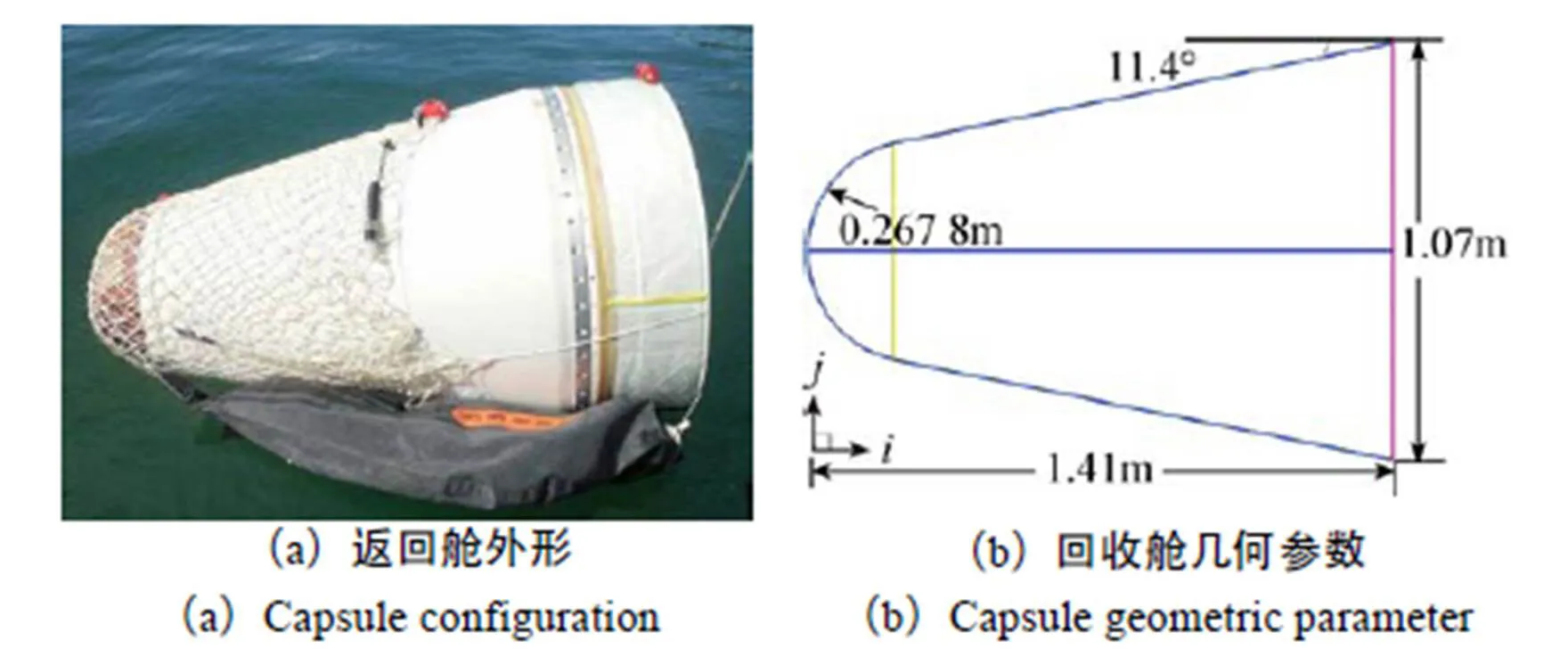
图1 卫星回收舱体结构参数

伴随流条件为相应高度的国际标准大气[14]，卫星返回至95km高空时速度7 860m/s，>28.45，以卫星球头半径为特征尺度的克努森数（）为0.216，属于过渡流区。详细来流参数如表1所示。文献[15]采用DSMC方法对三维钝头再入舱进行了化学平衡和非平衡两种工况计算，本文以此为参照，采用带二阶滑移条件的CFD方法进行模拟，并与开源的DSMC2V程序[16]二维计算结果进行对比分析。

表1 来流条件

Tab.1 Flow conditions

2 计算方法

2.1 数值方法

本文采用雷诺平均N-S方程求解，其形式可表示为[17]

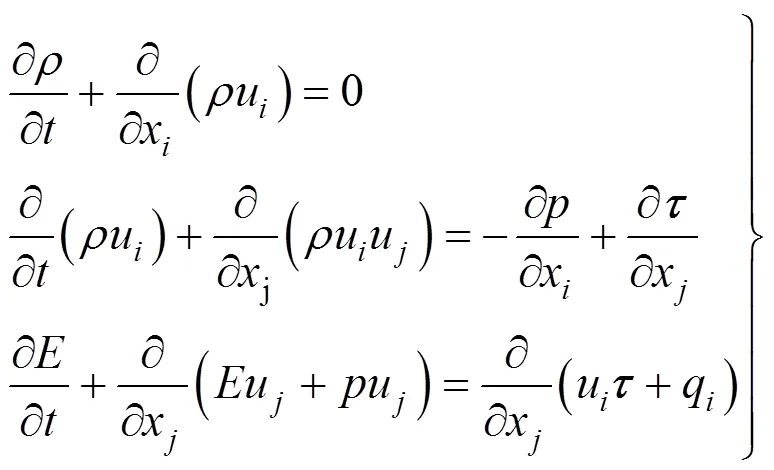
2.2 滑移条件

采用Beskok等[21]提出的二阶滑移条件，其壁面速度滑移和温度跳跃公式为

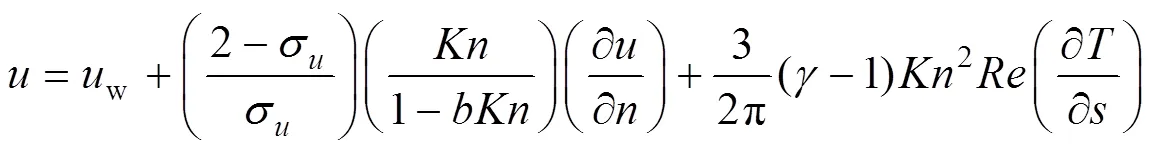
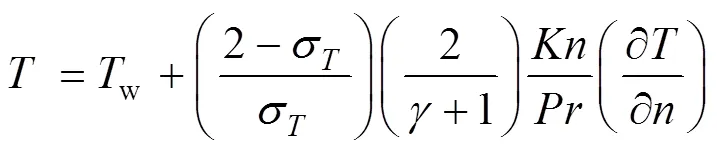
2.3 网格划分与边界条件

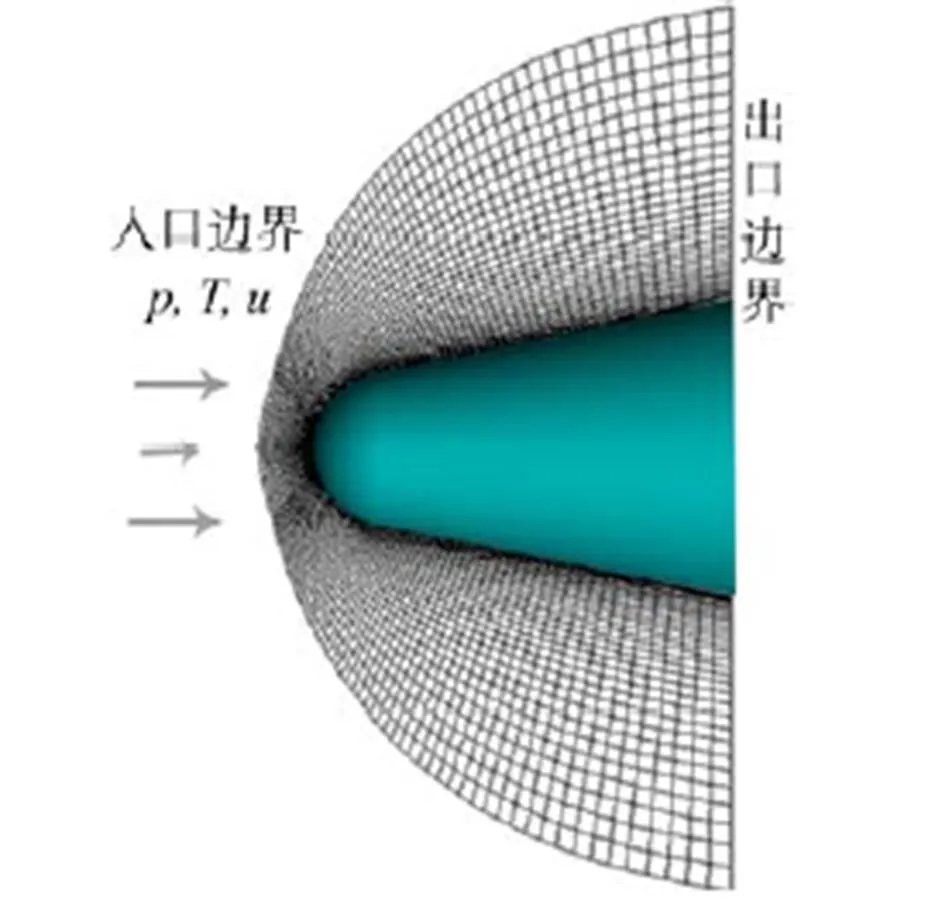
图2 对称面网格及边界条件

3 结果与讨论

3.1 网格无关性验证

物体壁面法向网格尺度对气动热模拟结果影响较大，为了消除网格因素的影响，采用由疏到密的5套网格，对二维轴对称模型进行了网格无关性测试。测试网格尺度、网格延伸率及计算获得壁面+如表2所示。

表2 测试网格参数

Tab.2 Test grids parameters

表3 不同网格下热流与压强系数峰值（误差）

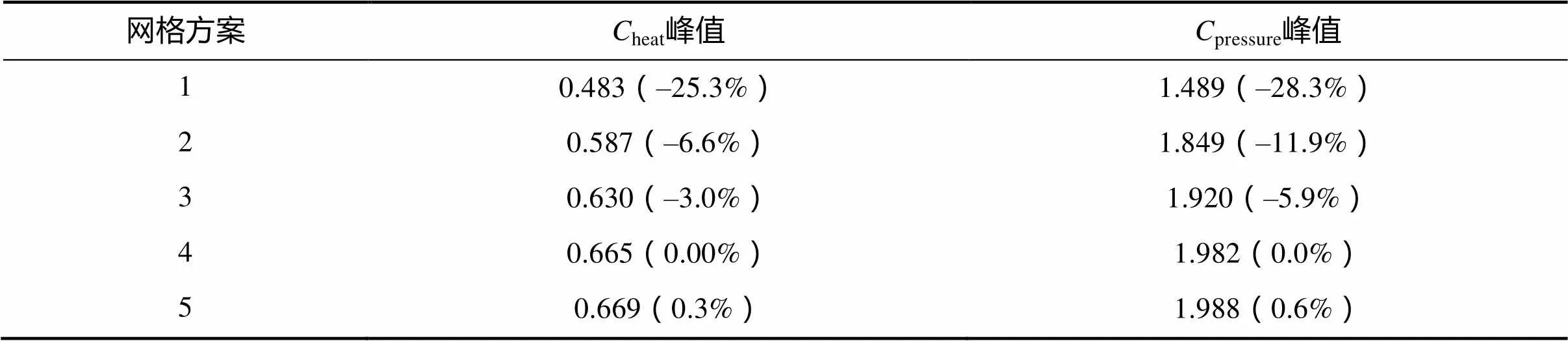
Tab.3 Heat flux & pressure coefficient with different grid（Difference）

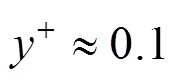
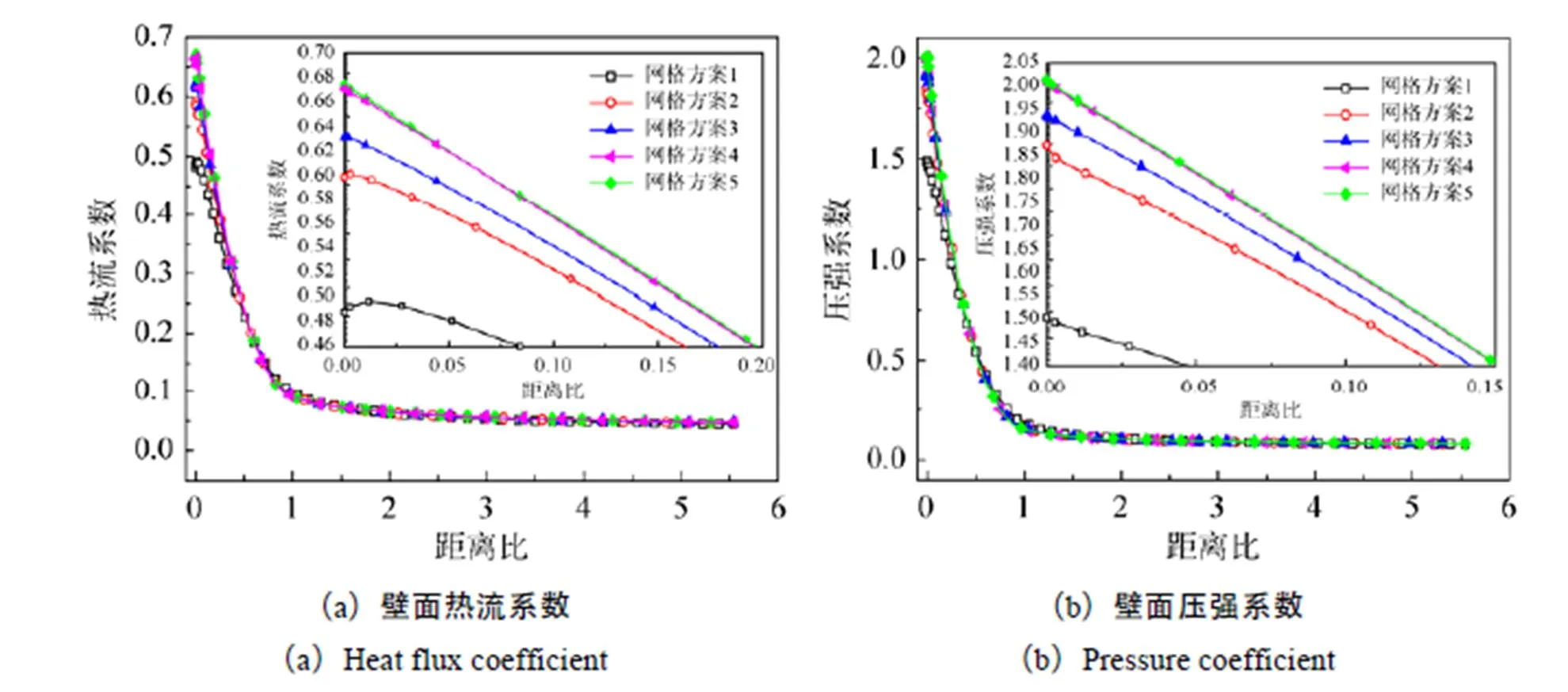
图3 不同网格尺度下壁面热流与压强系数

3.2 壁面热流与压强分布

为了分析带滑移条件的CFD方法模拟再入体气动热的能力，以DSMC2V计算结果为对照，对壁面热流、压强和流场参数进行对比分析。表4为驻点热流与压强系数峰值对比，可以看出：相对于DSMC非平衡流结果，CFD无滑移计算得到的量纲—热流系数峰值误差13.3%，添加滑移条件后，CFD滑移热流峰值误差降低至2.9%；CFD无滑移压强系数峰值误差2.8%，添加滑移条件后，压强峰值误差降低至0.5%。

表4 驻点热流与压强系数峰值（误差）

Tab.4 Peak heat flux & pressure coefficient（Difference）

图4（a）为三维壁面热流分布，可以看到热流峰值出现在球头驻点区域，并沿球头母线快速递减，锥体部分热流密度远低于驻点区，并且保持缓慢降低。图4（b）为沿舱体对称面母线的热流系数，可以看出，无滑移CFD方法模拟壁面热流明显高于DSMC结果，误差较大；添加滑移条件后模拟得到数据曲线与DSMC非平衡结果较为接近，误差较小。图4（c）给出了舱体表面三维压强分布，可以看出压强与热流分布规律较为相似，驻点区压强明显大于锥身区域，锥体部分压强保持在较低水平。图4（d）给出沿舱体对称面母线压强系数分布，可以看出无滑移CFD与带滑移条件CFD结果均与DSMC变化趋势相同，但添加滑移条件后，模拟得到的壁面压强更接近DSMC非平衡结果，误差较小。综合表4和图4可以看出，添加滑移条件的CFD方法能较为精确模拟过渡流区卫星回收舱表面热流分布和压强分布，满足工程上气动热预测需要。

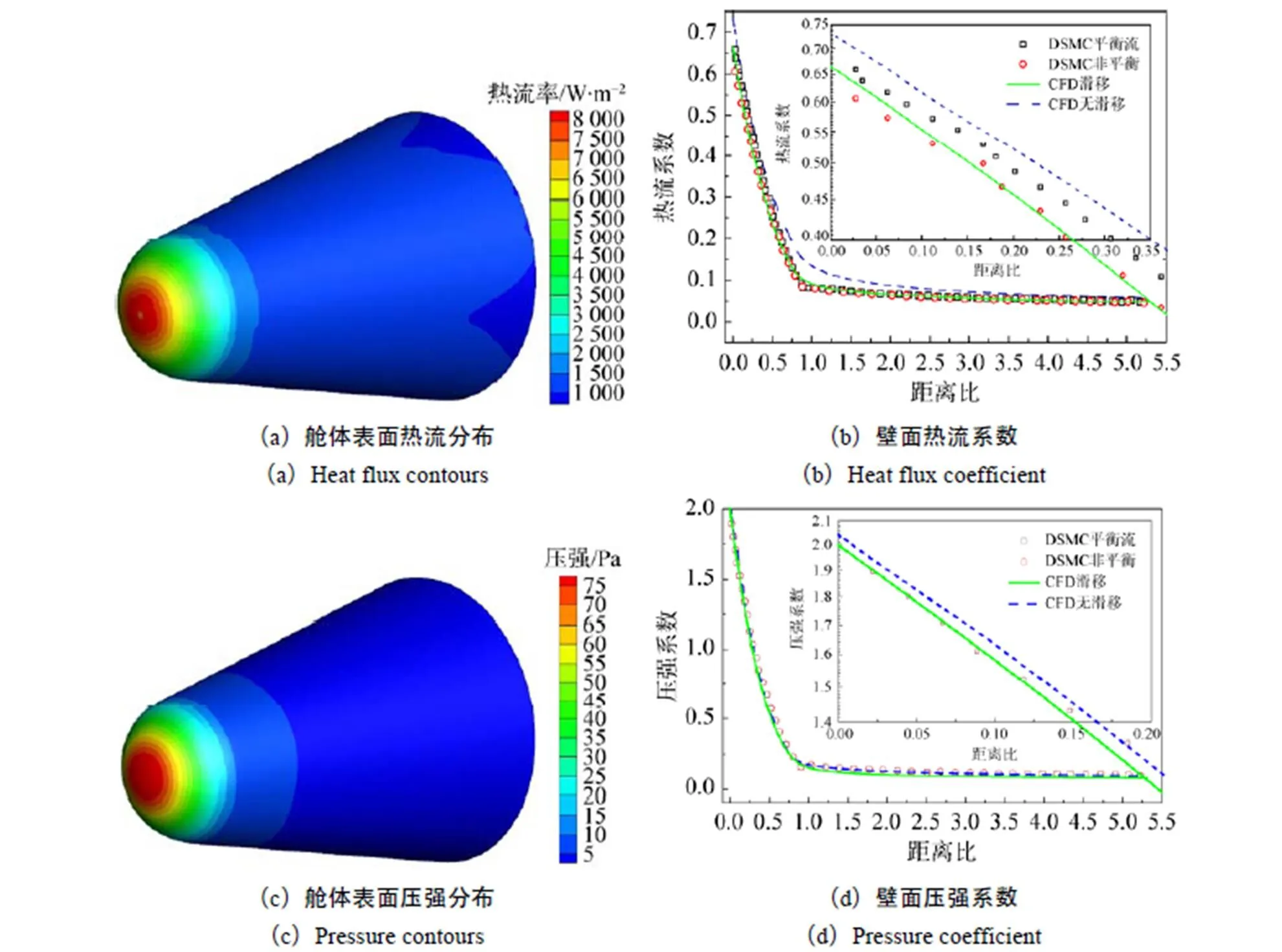
图4 壁面热流与压强分布

3.3 流场参数分布

综合对比图5（b）（d）（f）中是否添加滑移条件的两种CFD方法模拟结果，可以看出：添加滑移条件后，对返回舱壁面附近的速度和温度参数进行了矫正，进而造成壁面温度梯度变化，进一步改善壁面热流和壁面压强分布，使之更加接近真实状态。综合图4、图5可以看出，滑移条件对外流场压强、速度带来影响非常小，没有改变原有流场分布，也没有改善CFD方法模拟稀薄流区流场能力。

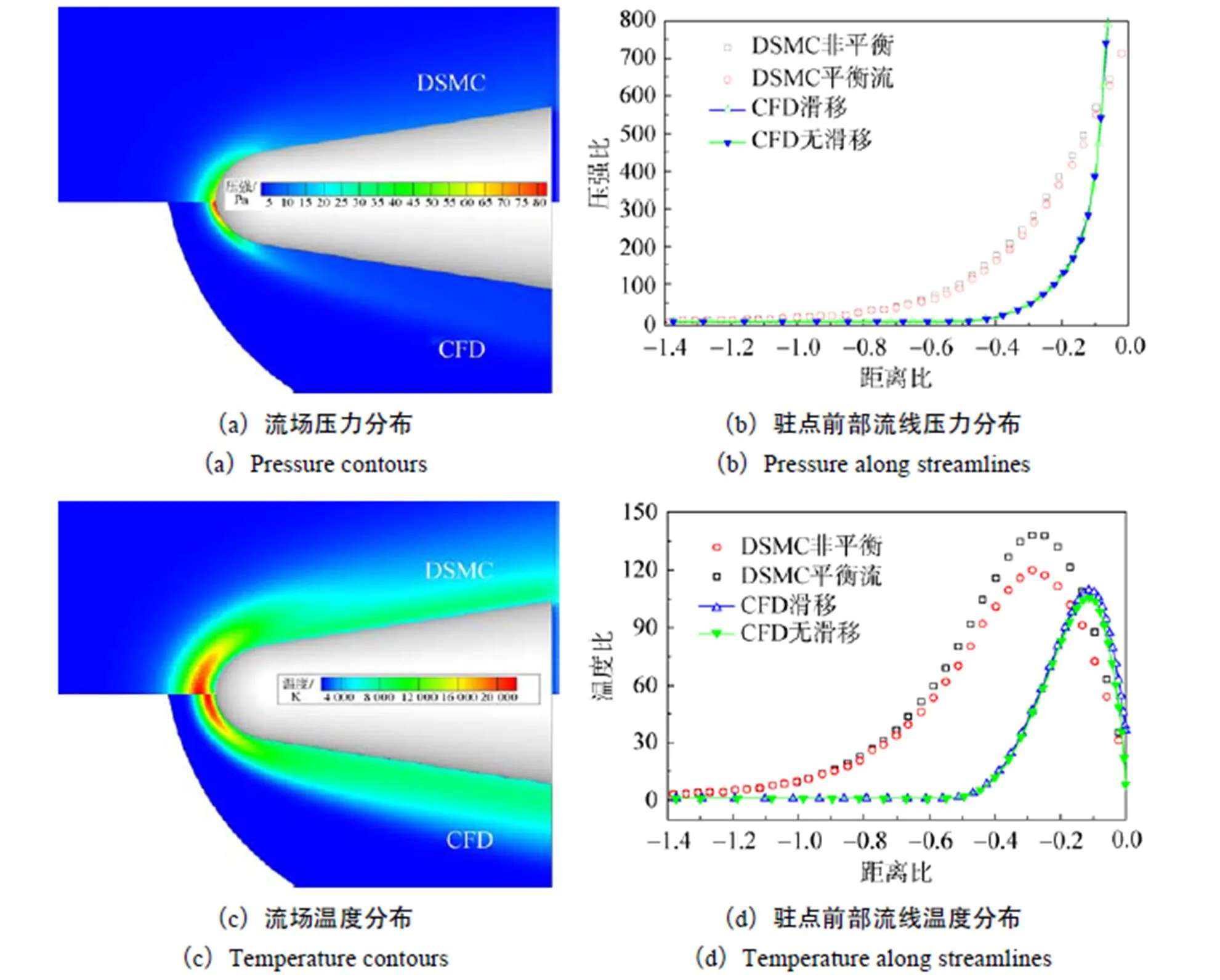
最后，对比CFD方法与DSMC方法在计算资源和计算效率上的差别。计算机配置为英特尔Core i5-650，3.2G Hz，双核4线程，内存8G，本文计算均采用单线程。两种方法计算至完全收敛的时长如表4所示。可以看出，DSMC由于依靠大量分子进行模拟，其计算量巨大，即使二维结果也需要计算20小时以上才能收敛，而三维CFD方法仅需要2小时左右。此外，必须看到，当进入稠密大气层时，DSMC方法效率大为降低，耗时将增加数十倍，但CFD方法计算效率变化不会太大。

表5 计算效率

Tab.5 Computational efficiency

4 结束语

本文以DSMC方法为对比，采用CFD方法模拟了克努森数不太大的过渡流区卫星回收舱表面压力和热流分布，研究了舱体母线热流、压强系数变化，分析了舱体前缘弓形激波厚度及流场温度、压强分布。数值模拟结果显示：

1）添加移条件后，CFD方法能够有效求解过渡流区回收舱气动热和壁面压强分布，模拟的母线方向壁面热流、压强系数与DSMC结果吻合较好，具有计算效率高、精度较高的优势，满足工程设计阶段气动热预测需求。

2）驻点前缘流线方向压力、温度、速度对比分析显示，添加滑移条件改善了壁面热流和压强分布，但没有改善CFD方法模拟稀薄流区流场的能力，得到的流场温度、压强、速度分布与DSMC结果有所差别。

[1] ANTONIO V, GIUSEPPE P. Nonequilibrium Aerothermodynamics for a Capsule Reentry Vehicle[J]. Engineering Applications of Computational Fluid Mechanics, 2009, 3(4): 543-561.

[2] 王希季. 中国返回式卫星的发展—纪念中国第一颗返回式卫星成功返回40周年[J]. 航天返回与遥感, 2015, 36(6): 1-5. WANG Xiji. Development of Chinese Returnable Satellite—To Commemorate the 40 Anniversary of the Successful Return of Chinese First Returnable Satellite[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(6): 1-5. (in Chinese)

[3] 邢连群. 返回式卫星烧蚀防热结构的工程计算[J]. 中国空间科学技术, 1991, 4(2): 26-34. XING Lianqun. An Engineering Computation of Ablative Thermal Protection Structure of Returnable Satellite[J]. Chinese Space Science and Technology, 1991, 4(2): 26-34. (in Chinese)

[4] 唐伯昶. 中国返回式卫星[J]. 中国航天, 2008(5): 8-17. TANG Bochang. Chinese Returnable Satellites[J]. Aerospace China, 2008(5): 8-17. (in Chinese)

[5] SCANLON T, WHITE J, BORG C, et, al. Open Source Direct Simulation Monte Carlo Chemistry Modeling for Hypersonic Flows[J]. AIAA Journal, 2015, 53(6): 1670-1680.

[6] MAZAHERI A R. Computational Aerothermodynamic Analysis of the Space Shuttle Orbiter Tile Overlay Repair with Different Geometries[R]. Reston, VA, US: AIAA, 2004.

[7] YANG G D, DUAN Y H, LIU C Z, et al. Approximate Prediction for Aerodynamic Heating and Design for Leading-edge Bluntness on Hypersonic Vehicles[R]. Reston, VA, US: AIAA, 2014.

[8] RODRIGO C, CRAIG W, MATTHEW K B, et al. Benchmark Numerical Simulations of Rarefied Non-reacting Gas Flows Using an Open-source DSMC Code[J]. Computers and Fluids, 2015(120): 140-157.

[9] MOSS J N, GLASS C E, GRANNE F A. DSMC Simulations of Apollo Capsule Aerodynamics for Hypersonic Rarefied Conditions[C]//Thermophysics and Heat Transfer Conference. San Francisco, CA, US, 2006.

[10] 贾居红. 临近空间高超声速气动热数值模拟研究[D]. 北京: 北京理工大学, 2017. JIA Juhong. Numerical Study on Hypersonic Aerothermodynamic of Near Space Flight Vichle[D]. Beijing: Beijing Institute of Technology, 2017.

[11] SCANLON T J, WHITE C, BORG M K, et, al. Open-source Direct Simulation Monte Carlo Chemistry Modeling for Hypersonic Flows[J]. AIAA Journal, 2015, 53(6): 1670-1680.

[12] FREIDOONIMEHR N, RASHIDI M M, YANG Z G, et al. Velocity Slip and Temperature Jump Effects for an Unsteady Flow over a Stretching Permeable Surfaces[J]. Thermal Science, 2016(1): 1-8.

[13] SANTOS W F. Aero-thermodynamic Analysis of a Reentry Brazilian Satellite[J]. Brazilian Journal of Physics, 2012, 42(5): 373-390.

[14] Standard Atmosphere Computations[EB/OL].[2018-3-23]. http://www-mdp.eng.cam.ac.uk.

[15] PAHLARINI R C, AZEVEDO J L. Thermochemical Nonequilibrium Computations of a Brazilian Reentry Satellite[J]. Journal of Spacecraft & Rockets, 2017, 54(4): 1-10.

[16] BIRD G A. The DSMC Method[M]. Oxford: Claredon Press, 2013: 57-92.

[17] WILCOX D C. Turbulence Modeling for CFD[M]. 3rd ed. California: DCW lndustries Inc, 2006: 243-249.

[18] GOLDBERG U C, OTA D K. A k-e Near-wall Formulation for Separated Flows[C]//AIAA 21st Fluid Dynamics, Plasma Dynamicsand Lasers Conference. Seattle, WA, US, 1990.

[19] GOLDBERG U C. Hypersonic Turbulent Flow Predictions Using CFD++[R].Reston, VA, US: AIAA, 2005.

[20] FURFARO D, SAUREL R. A Simple HLLC-type Riemann Solver for Compressible Non-equilibrium Two-phase Flows[J]. Computer & Fluid, 2015(111): 159-178.

[21] BESKOK A, KARNIADAKIS G E, TRIMMER W. Rarefaction and Compressibility Effects in Gas Microflows[J]. Transactions of the ASME, 1996, 118(9): 448-456.

[22] 毛宏霞, 贾居红, 傅德彬, 等. HIFIRE-1飞行器激波与边界层干扰气动热研究[J]. 兵工学报, 2018(3): 528-536. MAO Hongxia, JIA Juhong, FU Debin, et al. Research on Aero Thermodynamics and Influencing Factors for HIFIRE-1[J]. Acta Armamentarii, 2018(3): 528-536. (in Chinese)

[23] NASA Viscous Grid Spacing Calculator[EB/OL].[2018-3-30]. http://geolab.larc.nasa.gov/APPS/YPlus.

Aerothermodynamics Computations of Reentry Satellite in Transition Region

JIA Juhong1HU Lijie2

（1 Unit 91267, PLA Navy, Fuzhou 350015, China）（2 School of Information, Renmin University of China, Beijing 100872, China）

When the reentry satellite comes into the altitude of 95 km, its reentry Mach number is more than 20, high temperature wave surrounded the vehicle, and aero-heating becomes a serious problem. the Navier-Stokes (N-S) equations based on second-order velocity slip and temperature jump boundary conditions suggested by Beskok and Karniadakis are used to calculate the heat flux and pressure of the capsule, the results are compared with the direct simulation Monte Carlo (DSMC) method result, the DSMC2V opened by Bird is used. The influence of slip effects on aerothermodynamics properties are analyzed, the pressure contours, Mach numbers and temperature contours of flow field are studied. The result shows that, N-S equations with velocity slip and temperature jump changed the near wall flow contours, then it can calculate the aerothermodynamics and aerodynamics correctly, and has the advantage of high efficiency and high accuracy. Havever, the analysis of flow contours depicts, slip boundary condition do not change the out flow conditions. As a result, the simulated flow contours, along with the position and thickness of shock wave is a little different from the DSMC results. It can be conclude that this method is satisfied with the prediction of heat flux for reentry satellite in transition regime.

hypersonic; aerothermodynamics; capsule; Computational fluid dynamics; slip boundary conditions; reentry satellite

V211

A

1009-8518(2018)06-0037-09

10.3969/j.issn.1009-8518.2018.06.005

2018-07-20

贾居红，男，1989年生，2017年获北京理工大学宇航学院兵器科学与技术专业硕士学位，工程师。研究方向为再入体气动热问题。E-mail：jiajuhongbit@126.com。

胡丽杰，女，1995年生，现在中国人民大学信息学院攻读硕士学位。主要研究方向为微分方程数值解问题研究。E-mail：lily_950827@126.com。

（编辑：刘颖）