VVT正时链轮的模具优化设计
申小平,黄永强
VVT正时链轮的模具优化设计
申小平,黄永强
(南京理工大学 工程训练中心,南京 210094)
VVT正时链轮是汽车发动机中的关键零件,作为汽车传动机构具有较高的配合精度要求。本文基于粉末连续体,运用有限元deform软件对VVT正时链轮的三种不同设计方案下的压坯密度进行模拟分析。通过数值模拟仿真数据对模具进行改进及尺寸优化,提高压坯密度分布的均匀性,以实现VVT正时链轮采用粉末冶金近净成形的先进方法制造,并满足其对精度、密度、性能的要求。结果表明:设计上一下一的模具结构,在锁孔对应位置处上模冲设计漏粉穴,使得锁孔处处于过饱和的粉末实现移动,防止产生过压现象。当漏粉穴尺寸较小时,其过压现象得不到缓解,当漏粉穴尺寸较大时,锁孔周边粉末流失,形成低密度区,导致整体密度分布不均,将漏粉穴的体积设计为锁孔体积的2/3时,可获得密度分布最均匀的压坯。
粉末压制;有限元模拟;相对密度;VVT链轮
发动机可变气门正时系统(VVT,variable valve timing)通过配备的控制及执行系统对发动机凸轮的相位进行调节从而使得气门开启、关闭的时间随发动机转速的变化而变化,调整进气(排气)的量,和气门开合时间与角度。使进入的空气量达到最佳,提高燃烧效率。正时链轮是可变气门正时系统的关键部件,汽车发动机在工作过程中,在气缸内不断发生进气、压缩、爆炸、排气四个过程,并且每个步骤的时机都要与活塞的运行状态和位置相匹配,使进气与排气及活塞升降相互协调起来,正时链轮在发动机里面扮演了一个“桥梁”的作用,在凸轮轴的带动下将力量传递给相应机件。图1为正时链轮的零件图。近净成形技术可直接由粉末制成最终制品或接近最终形状的制品,而不需或只需少量机加工便可以达到制品的技术需求。与传统的金属加工方法相比,粉末冶金法制备材料利用率高、能耗低、经济效益好,是节能节材的先进工艺技术[1−2]。因此,在工业生产中被大量用于金属零件的制备,特别是在汽车制造领域有着广泛的应用[3]。对于生产油量控制套筒这种形状复杂的零件,正由近净成形先进制造方法取代传统的切削加工方 法[4]。运用有限元软件对粉末压制成形过程模拟是一种有效的设计方法,可发现生产过程中存在的问题,并提出有效的改进措施,从而做到早期评价,优化工艺参数,快速有效地确定模具的最终理想形状,提高生产效率,缩短研发周期,降低成本[5−6]。Deform有限元软件广泛应用于塑性成形工艺的模拟仿真,可用于分析各种塑性成形过程中的金属流动以及应变应力、温度、密度等物理场量的分布,提供材料流动、成形载荷、模具应力、密度分布和金属微结构等信息。运用不同的材料模型可分析残余应力,回弹问题以及粉末冶金成形等,并为模具仿真及其他相关工艺分析提供数据[7]。本文运用有限元deform软件对VVT正时链轮的三种不同设计方案下的压坯密度进行模拟分析。通过模拟数据对模具进行改进及尺寸优化,着重对带有逃粉穴设计的模具进行模拟并加以分析,以此来提高压坯密度分布的均匀性。
1 现有粉末冶金制造工艺方案、存在问题及改进方案
1.1 制造工艺方案
对于正时链轮的粉末冶金制造工艺方案:考虑到该款正时链轮的厚度较薄(总厚为6.5 mm),在后道工序中需要对齿部和锁孔处进行局部高频淬火处理,会产生较大的变形,难以保证产品的平行度和平面度,因此在压制工艺时需对毛坯的密度进行精确地控制,尽量保证各部位密度均匀性,避免在热处理过程中由于密度不均而产生开裂现象。本研究中采用上一下一的模具结构,上模冲开凿漏粉穴,保证压坯在锁孔处密度均匀,另外采用机加工的方法车出锁孔背面凸台及台阶。该方案模具零件包括阴模、上模冲(带逃粉穴)、下模冲、芯棒。其压形毛坯如图2所示。

图1 正时链轮的零件图

图2 正时链轮的压坯图
1.2 存在问题及实验方案
上述工艺方案得到的压坯存在以下问题:(1) 密度均匀性较差。从外观看,有亮有暗,色泽不均匀。通过分段密度测试可知,暗处和亮处密度相差达0.8 g/cm3。图3所示的阴影区域为高密度区。(2) 存在裂纹。部分压坯有裂纹,裂纹出现的位置通常在密度差大的区域。
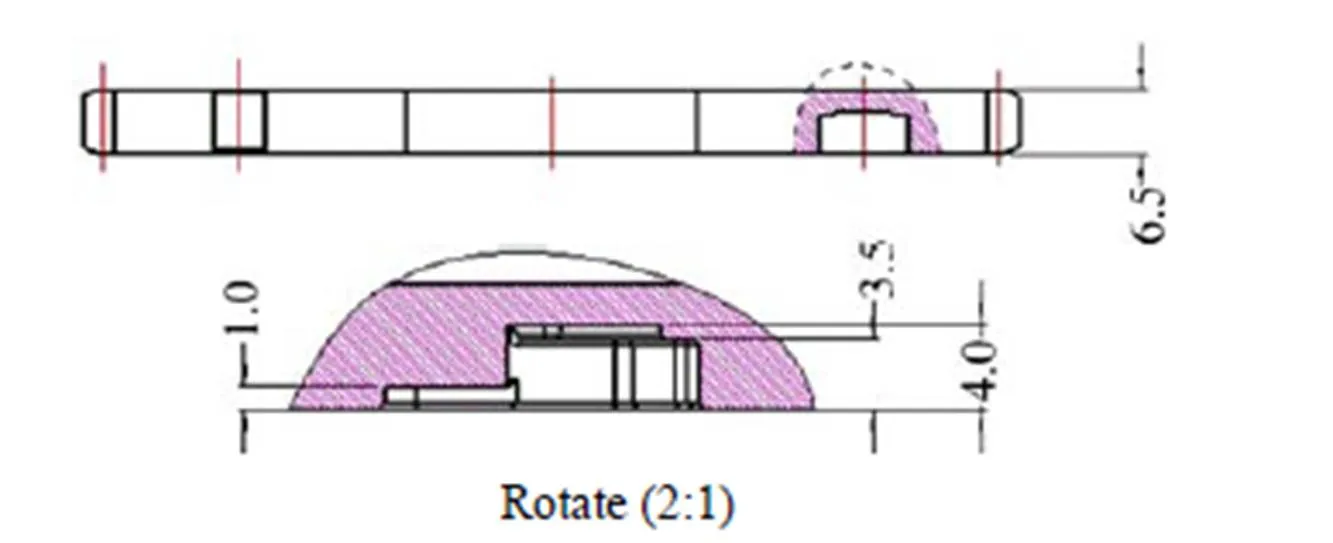
图3 压坯不良现象:密度不均匀及压坯裂纹分布
试验方案:(1) 方案一,直接采取上一下一的模具结构,上模冲不加逃粉穴。(2) 方案二,采取上一下二的模具结构,锁孔位置成形单独分冲。(3) 方案三,采用上一下一的模具结构,在锁孔对应位置的上模冲设计漏粉穴[4],使得此处多余粉料实现排除以防止锁孔区域过压。
2 模具改进方案的有限元分析
粉末体具有流动性,在一定程度上具有流体的特性,但粉末体在受压下又可变形具有固体的特性。本文针对粉末特有的性质,介于流体和固体之间,将粉末体选为Deform软件中的粘塑性porous模型,模具为刚性rigid模型,采用更新的拉格朗日方法对粉末压制过程进行模拟分析[7−8],基于模具不同改进方案下得到密度分布均匀的压坯为目的。材料参数如图4所示:粉末的松装相对密度为0.438,杨氏模量与其密度存在一定的关系,如图4(a)所示;泊松比用概率密度的正态分布函数表示[9],如图4(b)所示;流动应力应变曲线,如图4(c)所示;热膨胀系数为1.35×10−5。按装粉系数为=2建立有限元模型[10]。模拟过程:在三维作图软件中建立的坯料及模具组装模型转化为STL格式导入3D-Deform中,将粉坯模型进行属性定义及网格划分,定义模具属性以及各冲头的压制速度,采用残差或位移收敛,收敛精度为10×10−6。摩擦条件定义:采用修正的库伦摩擦模型,摩擦因数为0.2。
2.1 上一下一的模具结构,上模冲不加逃粉穴
采用上一下一的模具结构,上模冲不加逃粉穴设计方案,运用deform软件对粉末压制过程进行模拟研究,得到压坯的密度分布,如图5所示。由图可知,压坯P3处最大的相对密度值为0.97(密度为7.6 g/cm3,致密体密度为7.85 g/cm3),即锁孔区明显存在过压现象,这是由于下模冲为一个整体的冲头,不能对锁孔处粉末充填量进行调整,以充填系数为2计算,锁孔处理论的充填量为5 mm,但采用不加逃粉穴结构设计方案时,锁孔处的实际充填量为9 mm,因此在压制过程中会产生过压现象,导致压坯产生裂纹,甚至下模冲锁孔凸台崩断。通过密度分布图像可看出P4、P5处密度较其他区域较大,这是充填不可调造成的。另外,从图5对压坯密度纵向数据进行对比P1(0.946)>P2(0.837),P4(0.926)>P5(0.876),这是因为锁孔在压制过程中会发生粉末横向移动,相应地增加了P1和P4区域的充填量。
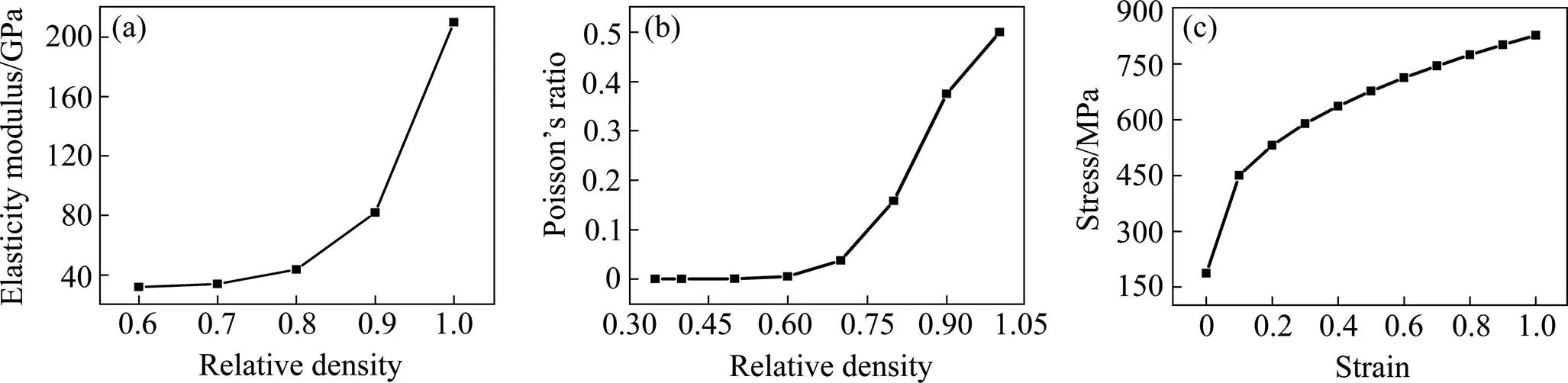
图4 材料参数的关系曲线
(a) Relationship between elasticity modulus and relative density; (b) Relationship between Poisson’s ratio and relative density; (c) Flow Stress
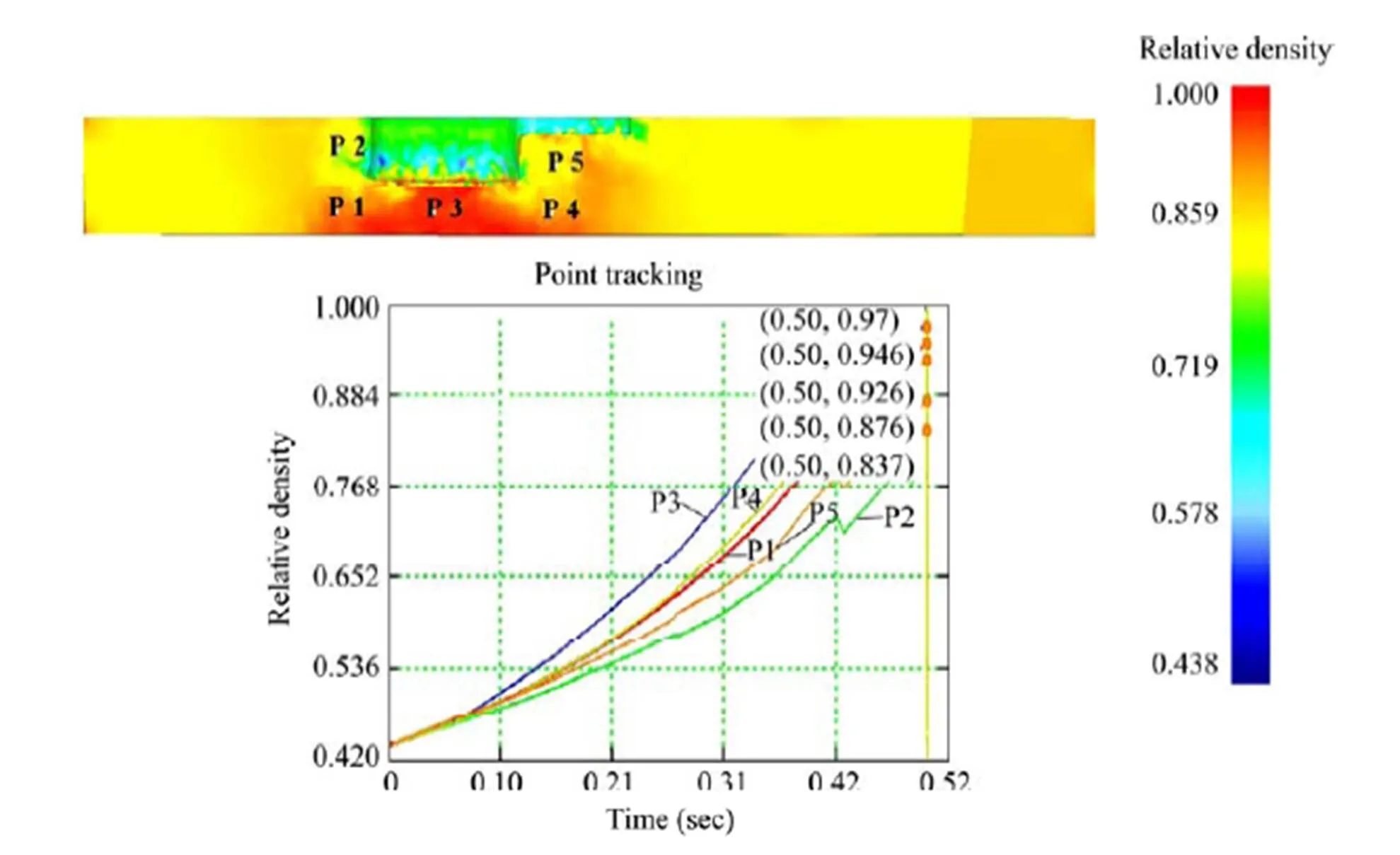
图5 压坯密度分布
2.2 上一下二的模具结构,锁孔处单独分冲
基于方案一锁孔处产生过压现象为锁孔处不能自由充填造成,对模具结构进行改进,采用方案二(上一下二的模具结构,锁孔处单独分冲)。图6为方案二得到的压坯密度分布图,图6显示,P3处密度得到极大改善,相对密度值为0.93(密度为7.2 g/cm3),这是由于将下模冲分冲,锁孔处单独成冲[12],可以调整其充填量,因而P3处密度可以调整,不会产生过压现象。但采用该方案存在一个问题:由于锁孔处的模冲存在一个段差(锁头与锁尾段差为3 mm),从图6可知,P3与P5处的密度差值较大,相对密度差值达到0.2(密度差值为1.5g/cm3)。所以存在一个矛盾,当P3处达到合适密度值,P5处不能成形,当P5处达到合适密度值时,P3处会出现过压现象。同时考虑后续存在锁孔高频热处理工艺,由于相邻区域存在较大的密度差,会导致工件变形过大或工件开裂问题,因而方案二存在很大的局限性。
2.3 上一下一的模具结构,在锁孔对应位置处上模冲设计漏粉穴,并优化漏粉穴的尺寸
通过对方案一及方案二进行分析,为解决锁孔处的密度分布不均问题,从而考虑在压制过程中增加锁孔处的排粉量,避免出现过压现象,以此提高零件的整体密度,改善密度分布的均匀性。在此,采用上模冲开凿漏粉穴的设计方案,并且对比在不同尺寸的漏粉穴下采用有限元模拟分析得到压坯相对密度的分布情况,从而达到优化压坯密度的效果。结合实际经验,对于上模冲开凿漏粉穴时,为便于产品脱模,漏粉穴需要设计脱模斜度,一般为20°~45°。在本方案中脱模斜度设计为30°,另外漏粉穴的斜面与凸台平面设计圆角过渡为R2。
图7所示为设计不同尺寸(占压坯锁孔体积的比例)的漏粉穴得到的生坯相对密度分布图。从图中可知,随漏粉穴尺寸增大,锁孔区域处的密度均有所降低,这是由于在压制过程中锁孔处的粉末移向漏粉穴的粉末增多[15],排粉量加大,充填系数降低。基于设计目的,主要对高密度区P3处的数据进行研究,发现随漏粉穴尺寸增大,P3处的相对密度值减少,当漏粉穴的尺寸由1/3增加到1时,P3处的相对密度值由0.929降低至0.861。由于漏粉穴尺寸的增大,压制过程中有限的粉末(充填量一定)需成形更大的空间,因此P3处的密度减小。此处,漏粉穴P6处的密度也随着漏粉穴尺寸的增大而降低,相对密度值由0.924降至0.772。从压坯密度分布图中可知,P2及P5处密度相对于其他区域较低,这是由于上模冲的漏粉穴径向尺寸与锁孔的径向尺寸一致,在压制时,锁孔处由于带有漏粉穴与其他区域存在压制速度不一致,即粉末受压时P2及P5处先受压,该处粉末产生横向流动和纵向移动进入到漏粉穴空间中。当漏粉穴处粉末成形时,P2及P5处已先成形具有一定密度的坯料,粉末不能从P3处流回到P2和P5处。
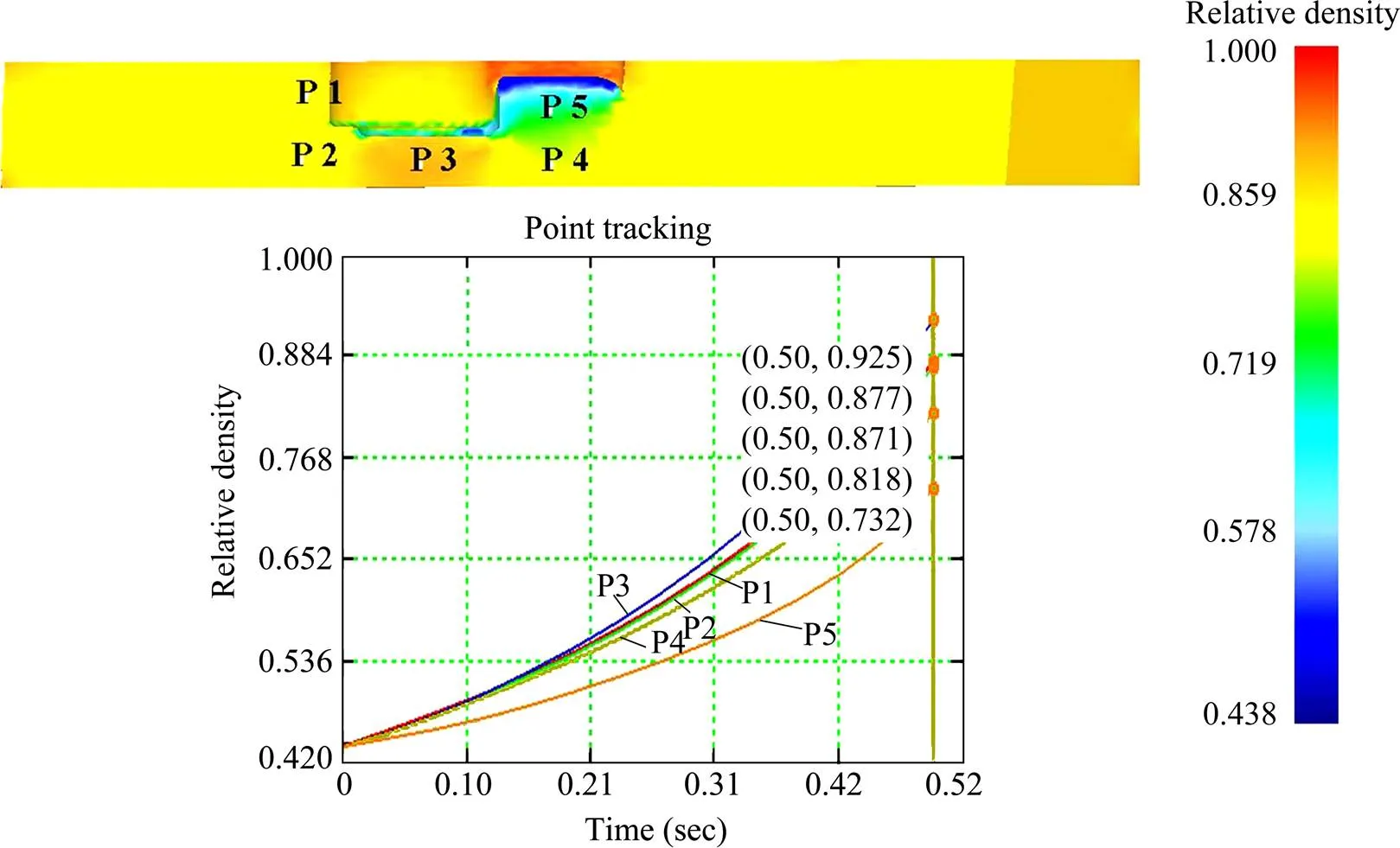
图6 压坯密度分布图
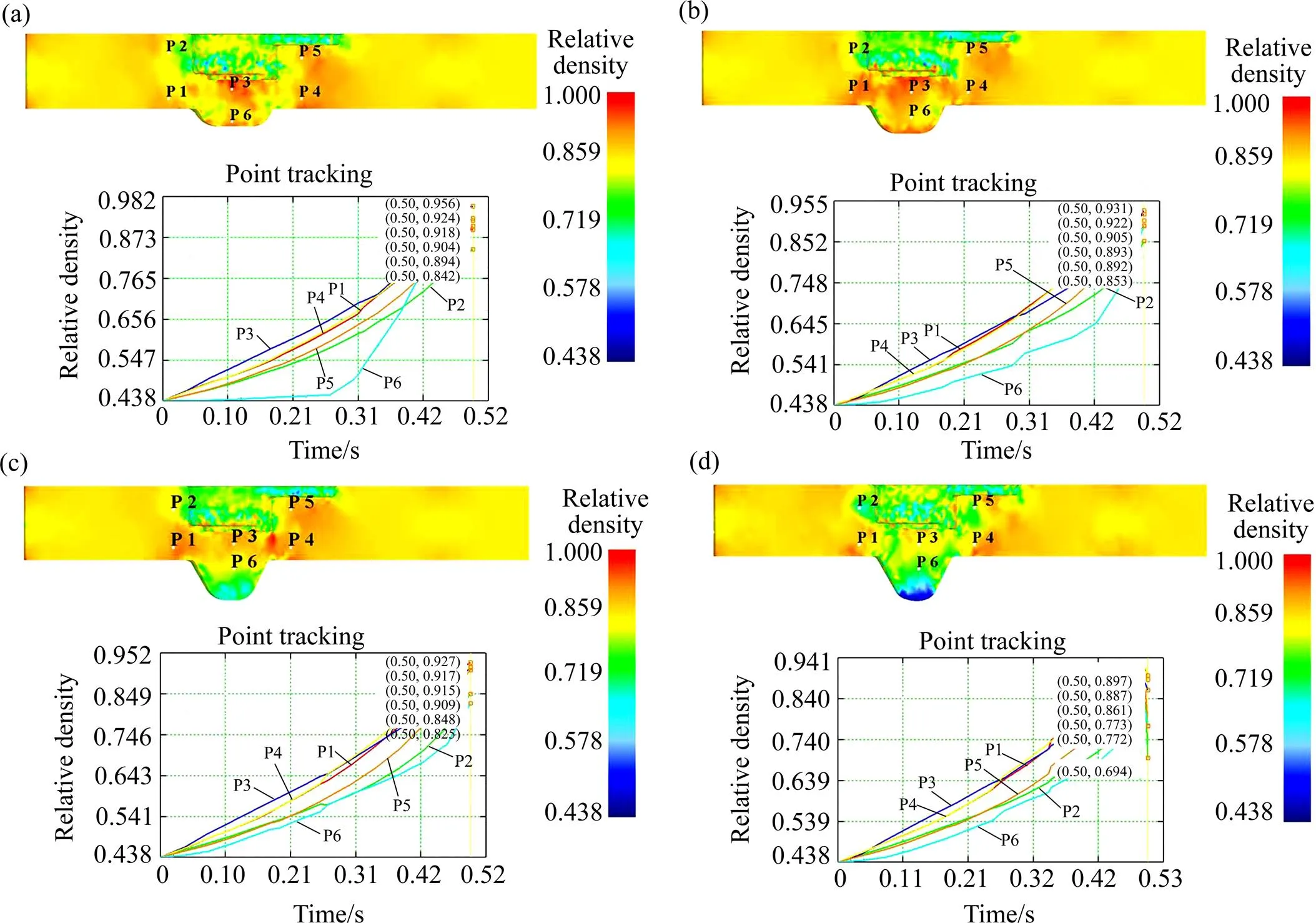
图7 基于不同尺寸漏粉穴(占压坯锁孔体积的比例)的压坯相对密度分布
(a) 1/3; (b) 1/2; (c) 2/3; (d) 1
为分析漏粉穴尺寸对其压坯总体密度分布均匀性的影响,在图7有限元模拟中的4个点的相对密度中,引入一目标函数=max−min,即以相对密度极差表示压坯密度分布的均匀性。数值化的获得了最佳宽度尺寸的漏粉穴设计方案。
由表1可知,随漏粉穴尺寸(占压坯锁孔体积的比例)增大,相对密度极差的数值先减小后增大,当上模冲的漏粉穴设计成一定尺寸时,压坯具有较均匀的密度。压坯相对密度极差与漏粉穴尺寸并不呈线性关系,当开凿漏粉穴的体积较小时,受压处(P3)过多的粉末不能完全逃逸,在压制过程中该处依然存在受压现象。当开凿漏粉穴的体积较大时,受压处(P3区)及锁孔周围处(P1,P2,P4和P5)粉末逃逸过多,造成锁孔周围处密度较低,甚至不能成形。漏粉穴的尺寸变化对压坯的相对密度极差影响显著,漏粉穴尺寸由1/3增至1/2,值变化极大,由0.114降为0.078。随着开凿的漏粉穴的尺寸持续增大,其影响效果渐弱甚至无效,漏粉穴尺寸由1/2增至2/3,值基本处于同一水平线上,变化不大,由0.078变为0.079。这是由于锁孔受压处(P3)粉末相对处于过饱和状态,在压制过程时,锁孔及其周围粉末可以通过横向和纵向流动的方式来调整装粉系数,从而使该区域密度均匀,所以设计在该范围内的漏粉穴可保证压坯具有极好的密度分布。当漏粉穴尺寸继续增大时,漏粉穴的空间足以保证过压的粉末完全溢出,并需要锁孔周围处的粉末来弥补,降低了该区域的粉末充填量,进而影响压坯的密度分布均匀性。所以当漏粉穴尺寸由2/3变为1时,值变化极大,由0.079增至0.203。结合分析优化漏粉穴的尺寸范围为1/2到2/3。

表1 漏粉穴尺寸与相对密度极差的关系

表2 密度测量数据
2.4 优化模具结果
通过上述分析可知,采用上一下一的模具结构,在锁孔对应位置处上模冲设计漏粉穴,上模冲漏粉穴体积设计为锁孔体积的2/3,漏粉穴的拔模斜度设计为30°,过渡圆角为R2,漏粉穴的径向尺寸比锁孔的径向尺寸单边小0.5 mm,采用改进后模具得到的粉坯密度分布如图8所示。
图9为在优化模具结构设计方案后得到的实体压坯图,采用阿基米德比重法测量压坯的锁孔及面部密度,测量结果如表2所示。通过数据分析,锁孔处的平均密度为6.90 g/cm3,面部的平均密度为7.06 g/cm3,锁孔处密度低于面部密度。在图7(c)中的密度分布图中,齿部密度可由P3和P6的平均值表示,而面部密度可由P1和P4的平均值表示。通过对比数据(P3+ P6)/2<(P1+P4)/2,发现压坯的实测数据与有限元分析数据是相吻合的。

图8 基于改进模具下的压坯密度分布

图9 优化模具结构后得到的压坯
3 结论
1) 基于上一下一的模具结构,上模冲不加逃粉穴设计方案:方案模具结构简单,产品后续加工量少(不需要车凸台),但由于不能自由调整锁孔处的装粉量,在锁孔处易出现过压现象,导致压坯密度不均而产生裂纹。
2) 基于上一下二的模具结构,锁孔处单独分冲设计方案:方案增加一个下模冲,在充填时能调整锁孔处的粉末充填量,可有效控制密度,避免过压。但由于模冲存在一个段差(锁头与锁尾段差为3 mm),因而不能兼顾该模冲各部位的适宜充填量,导致该区域密度分布不均,会影响后续的高频热处理工艺,导致变形量大甚至裂纹产生。
3) 基于上一下一的模具结构,在锁孔对应位置处上模冲设计漏粉穴方案:方案使得锁孔处处于过饱和的粉末移动,防止产生过压现象。当漏粉穴尺寸较小时,过压现象得不到缓解;当漏粉穴尺寸较大时,锁孔周边粉末流失,形成低密度区,导致整体密度分布不均,将漏粉穴的体积设计为锁孔体积的2/3时,可获得密度分布均匀的压坯。
[1] BRAIN DERBY. Structure properties of porous materials and powders used in different fields of science and technology[J]. Engineering Materials and Process, 2014, 4(2): 76−81.
[2] 黄春曼. 数值模拟在粉末冶金零件压制中的应用[J]. 现代制造工程, 2009, 1(5): 9−11. HUANG Chunman. Numerical simulation in suppression of powder metallurgy parts[J]. Modern Manufacturing Engineering, 2009, 1(5): 9−11.
[3] 李元元, 肖志俞, 陈维平, 等. 粉末冶金高致密化成形技术的新进展[J]. 粉末冶金材料科学与工程, 2005, 10(1): 1−9. LI Yuanyuan, XIAO Zhiyu, CHEN Weiping, et al. New progress of powder metallurgy high density forming technology[J]. Material Science and Engineering of Powder Metallurgy, 2005, 10(1): 1−9.
[4] 周作平, 申小平. 粉末冶金机械零件使用技术[M]. 北京: 化学工业出版社, 2005: 45−53. ZHOU Zuoping, Shen Xiaoping. Powder Metallurgy Machinery Parts and Practical Technology[M]. Beijing: Chemical Industry Press, 2005: 45−53.
[5] 周照耀, 李元元. 金属粉末成形力学建模与计算机模拟[M]. 广州: 华南理工大学出版社, 2011: 96−99. ZHOU Zhaoyao, LI Yuanyuan. Mechanical Modeling and Computer Simulation of Metal Powder Forming[M]. Guangzhou: South China University of Technology Press, 2011: 96−99.
[6] CEDERGREN J, SORENSEN N J, BERGMARK A. Three- dimensional analysis of compaction of metal powder[J]. Mechanics of Materials, 2002, 34(2): 43−59.
[7] 张莉, 李升军. DEFORM在金属塑性成形中应用[M]. 北京: 机械工业出版社, 2009: 35−39. ZHANG Li, LI Shengjun. DEFORM Application in Metal Forming[M]. Beijing: Machinery Industry Press, 2009: 35−39.
[8] 胡建军, 李小平. DEFORM-3D塑性成形CAE应用教程[M]. 北京: 北京大学出版社, 2011: 62−65. HU Jianjun, LI Xiaoping. DEFORM-3D Plastic Molding CAE Application Tutorial[M]. Beijing: Peking University Press, 2011: 62−65.
[9] 方伟, 何新波, 张瑞杰,等. 粉末注射成形充填过程中粉体分布的数值模拟[J]. 粉末冶金材料科学与工程, 2013, 18(2): 149−154. FANG Wei, HE Xinbo, ZHANG Ruijie,et al. Numerical simulation of powder volume fraction variation during powder injection molding filling flow process[J]. Material Science and Engineering of Powder Metallurgy, 2013, 18(2): 149−154.
[10] HOSSEIN K Z. Improvement in robustness and computational efficiency of material models for finite element analysis of metal powder compaction and experiment validation[J]. International Journal Advanced Manufacturing Technology, 2013, 68: 1785− 1795.
[11] 王德广, 吴玉程, 焦明华, 等. 不同压制工艺对粉末冶金制品性能影响的有限元模拟[J]. 机械工程学报, 2008, 44(1): 205− 211. WANG Deguang, WU Yucheng, JIAO Minghua, et al. Finite element simulation of different processes affecting pressing powder metallurgy products performance[J]. Journal of Mechanical Engineering, 2008, 44(1): 205−211.
[12] 申小平, 黄永强, 徐旭东,等. 柴油机油量控制套筒的模具优化设计[J]. 粉末冶金材料科学与工程, 2016, 21(4): 618−625. SHEN Xiaoping, HUANG Yongqiang, XU Xudong, et al. Optimization design of the mould for oil-quantity-controlling[J]. Material Science and Engineering of Powder Metallurgy, 2016, 21(4): 205−211.
[13] 高锦张. 塑性成形工艺与模具设计[M]. 北京: 机械工业出版社, 2001: 74−78. GAO Jinzhang. Plastic Forming Process and Die Design[M]. Beijing: Machinery Industry Press, 2001: 74−78.
[14] MEFTAH H, HEDI C. Modeling the powder compaction process using the finite element method and inverse optimization[J]. International Journal Advanced Manufacturing Technology, 2011, 56: 631−647.
[15] 尹键, 张红波, 熊翔, 等. 多孔体密度对C/C-Cu复合材料压缩性能的影响[J]. 粉末冶金材料科学与工程, 2014, 19(6): 989−993. YIN Jian, ZHANG Hongbo, XIONG Xiang, et al. Effect of porous C/C substrate density on compressive property of C/C-Cu composites[J]. Material Science and Engineering of Powder Metallurgy, 2014, 19(6): 989−993.
Optimization design of the VVT-Cam sprocket
SHEN Xiaoping, HUANG Yongqiang
(School of Material Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
VVT-Cam sprocket is a key part of automobile engine, which consequently require a relatively high matching precision as an automobile transmission mechanism. In this paper, based on the continuum powder material model, a simulation analysis of the density distribution of the green compact under three schematic designs was carried out using the finite element software- DEFORM. The structural and dimensional optimization of the mold and the improvement of the uniformity of density distribution were realized through the numerical simulation analysis. The results prove that the optimal design can satisfy the accuracy, density and performance requirements for the sprocket manufactured by the advanced net forming method of powder metallurgy. Aupper and a bottom die structure with a powder leaking hole at the corresponding position of the keyhole is designed, so that the supersaturated powder at the keyhole can be moved and the phenomenon of overpressure can be prevented. When the size of leaking hole is small, the overpressure phenomenon can not be alleviated. When the size of leaking hole is large, the powder around the keyhole loses, forming a low density area, resulting in uneven overall density distribution. When the volume of the powder leakage hole is designed as 2/3 of the keyhole volume, the blank with the most uniform density distribution can be obtained.
powder compaction; finite element simulation; relative density; VVT sprocket
TG38
A
1673-0224(2018)06-600-07
2018−05−23;
2018−06−12
申小平,高级工程师。电话:025-84315396;E-mail: xpshen171@163.com
(编辑 高海燕)

