基于子模型法的高堆石坝坝基廊道抗震安全性研究
曹学兴,何蕴龙,迟福东,张 丹,熊 ,余记远
(1.华能澜沧江水电股份有限公司, 云南 昆明 650214;2.武汉大学 水资源与水电工程科学国家重点实验室, 湖北 武汉 430072;3.中国电建集团 成都勘测设计研究院有限公司, 四川 成都 610072;4.长江勘测规划设计研究有限公司, 湖北 武汉 430010)
深厚覆盖层上的高心墙堆石坝,坝基与坝体结合部位的防渗,是大坝防渗的关键[1],结合部位发生破坏,最终可能会导致大坝的破坏,对下游基础设施及大众安全、社会稳定产生严重威胁,后果不堪设想[2]。坝基深厚覆盖层一般采用混凝土防渗墙防渗,防渗墙高出坝基面插入心墙或在其坝基面处设置灌浆廊道与心墙连接。国内一些深厚覆盖层上高土石坝工程,为做好防渗,帷幕灌浆量较大,如大渡河瀑布沟、宝兴河跷碛等,为避免帷幕灌浆施工占用直线工期,加快施工进度,在坝基防渗墙与心墙结合部位均采用灌浆廊道连接,廊道内也便于布置安全监测仪器,加强对大坝的安全监测,在运行出现异常情况时为采取更多有效的措施提供了可能性。
大渡河长河坝砾石土心墙堆石坝坝高240 m,建于覆盖层最大厚度79.3 m的地基上,处于高地震烈度区,100年超越概率2%基岩水平峰值加速度为0.359g。该工程采用两道全封闭混凝土防渗墙,在主防渗墙顶设置了城门洞型式的廊道与心墙连接,如图1(a)、图1(b)所示,廊道内部尺寸3 m×4 m,侧墙厚2 m,底板厚3 m。该廊道在河床段沿纵向不设结构缝,原设计在基岩覆盖层分界线处分缝与两岸灌浆平洞连接,但采用类似结构的跷碛及瀑布沟等工程均出现了廊道开裂及止水破坏的现象[3-4]。经深入研究后,坝基廊道改为深入基岩1 m与两岸灌浆平洞有缝连接[5],如图1(c)所示。
目前已有的研究成果对深厚覆盖层上坝基廊道的应力变形规律认识尚不成熟,长河坝大坝坝高和地震烈度远超过已建类似工程,坝基廊道安全性问题更为突出,开展坝基廊道的应力变形规律研究对保障坝基廊道的安全性有重要意义。本文采用基于子模型法[6-9]的三维非线性有限元对深厚覆盖层中的坝基廊道进行了精细模拟,先后对大坝-坝基整体及坝基廊道进行了地震时程动力计算,分析坝基廊道的静动力特性,评价其抗震安全性。
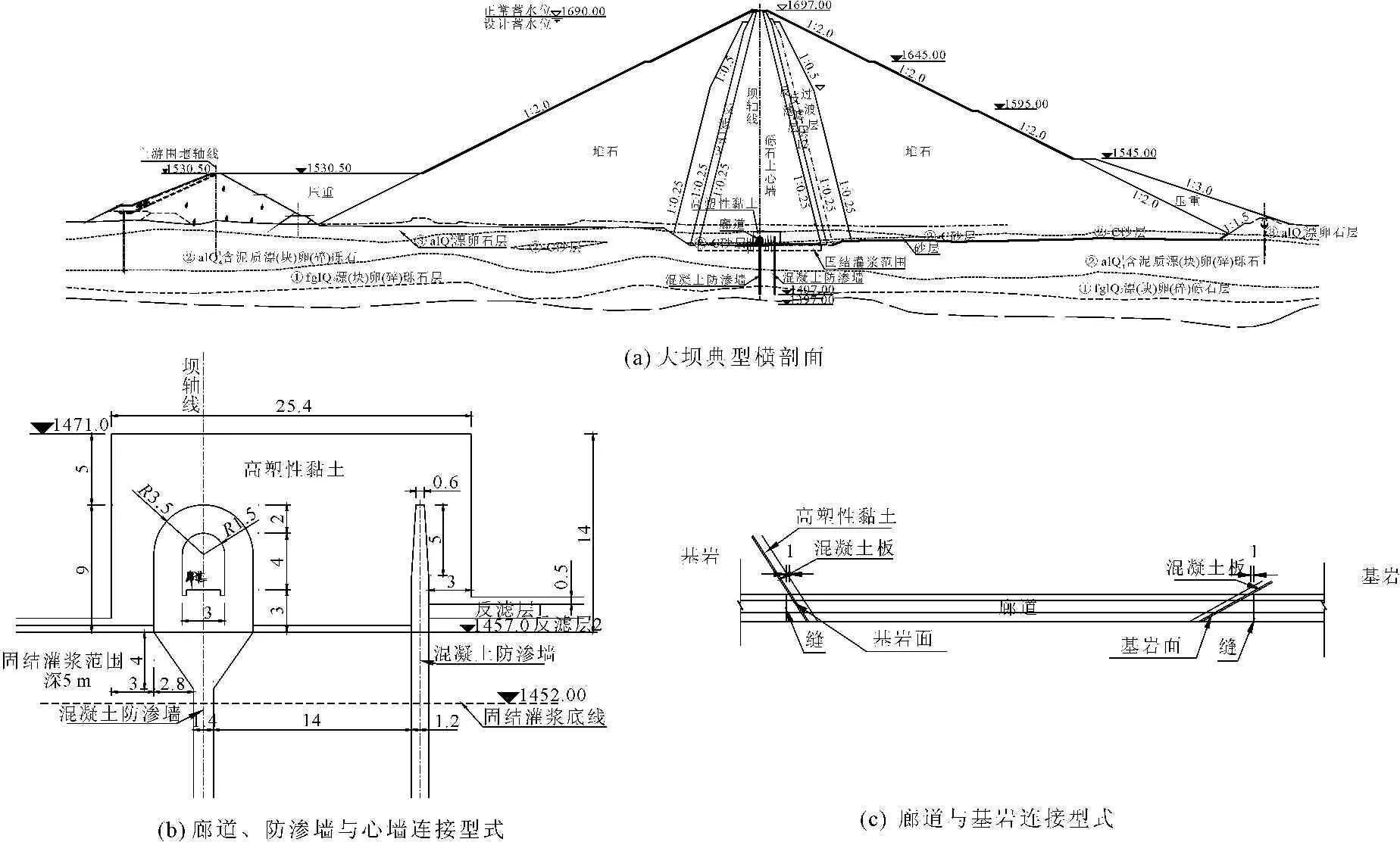
图1大坝结构型式图
1 考虑围压效应的土石材料动本构模型
静力计算模拟了坝体分层填筑与蓄水过程,在静力计算基础上进行动力计算。动力计算对传统的Hardin-Drnevich模型进行了改进,以反映围压对材料动力特性影响[10-12],模型基本表达式如下:
G/Gmax=1/(1+(γd/γr)m)
(1)
λ=a3+a4(1-G/Gmax)a5
(2)
式中:G为等效剪切模量;Gmax为最大剪切模量;γd为动剪应变幅值;γr为参考剪应变幅值;m为曲线形状系数;λ为等效阻尼比;a3为基本阻尼比;a4、a5为形状系数。
通过图2可以看出,改进的Hardin-Drnevich模型可较好反映长河坝大坝心墙料和堆石料在动力条件下的材料特性。
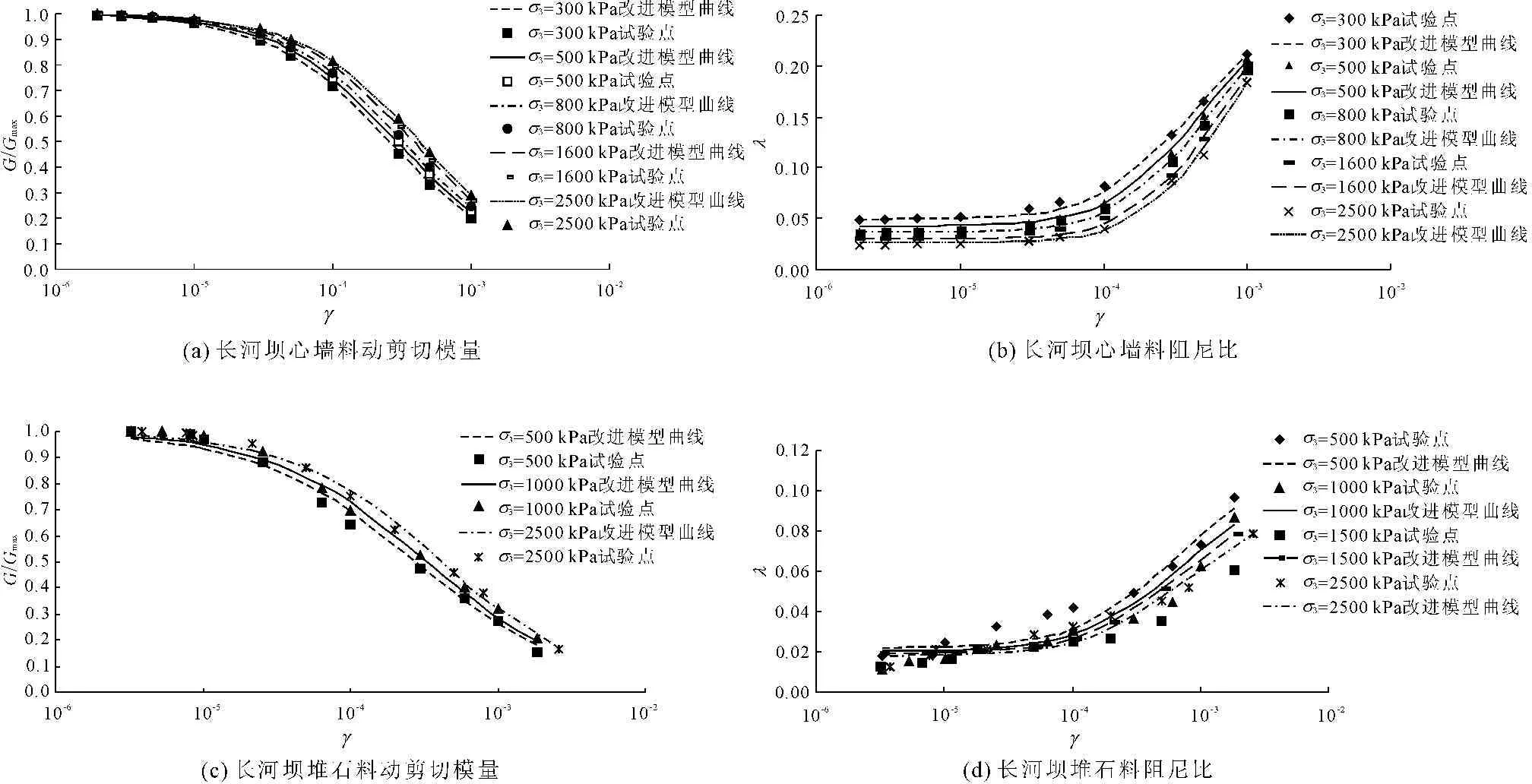
图2大坝材料动力特性参数曲线与试验点对比
2 计算模型和材料参数
2.1 有限元计算模型
真实模拟了工程地形条件,建立了整体有限元整体模型和局部子模型,如图3所示,整体模型有21 586个单元,子模型有13 176个单元。采用有厚度薄层单元模拟防渗墙与上下游侧覆盖层、防渗墙与周边基岩以及廊道与两岸平洞接缝等接触[14-15]。子模型模拟的坝基防渗体系的细部构造如图4所示。


图3 有限元模型
图4子模型细部
2.2 材料参数与计算荷载
土石料与接触面力学参数见文献[10],廊道、防渗墙和基岩均采用线弹性模型,动力采用无质量基岩模型计算,弹性模量在静力的基础上提高30%。地震波通过SHAKE91程序反演后进行输入,地震计算时长30 s,水平向峰值为0.29g,竖直向峰值为0.193g。地震波时程曲线如图5所示。

图5加速度时程曲线
3 静力条件下坝基廊道应力变形分析
在上覆坝体压力及廊道自身重力作用下,廊道出现竖直向下的挠曲变形,在防渗墙的带动下发生向下游挠曲变形。两种变形组合后在廊道轴线方向产生较大的拉压应力,廊道两端上游受拉,下游受压,河床中部上游面受压、下游面受拉。因坝基岩体的约束,基岩面处出现了明显的应力集中现象,左右岸1/4跨位置上游面压应力较大,下游面拉应力较大。表1列出了静力条件下廊道沿各方向的变形和正应力极值。

表1 坝基廊道应力变形最值
4 地震条件下廊道应力变形分析
4.1 整体应力变形状态
(1) 加速度和动位移反应。由于坝基廊道埋藏于坝体与基础内部,其加速度和动位移等动力反应不大,顺河向较其他两个方向反应较大,图 6给出了廊道顶部沿坝轴线三个方向加速度和动位移的分布曲线。顺河向加速度在河床中部反应较大,最大值为6.0 m/s2,横河向和竖直向加速度沿廊道长度方向分布比较均匀;廊道顺河向动位移也是在河床中部明显较大,极值为2.7 cm,横河向和竖直向动位移沿廊道长度方向变化不大。
图6廊道顶部动力反应
(2) 动应力反应。图7给出了廊道横河向最大动应力,图8为动静叠加后廊道横河向正应力分布图。地震作用下,廊道在两岸基岩面处有明显的动应力集中,横河向应力值较大,在右岸基岩面处廊道上游面底部出现最大动拉应力值2.14 MPa,右岸基岩面处廊道下游面底部出现最大动压应力值为2.23 MPa;两岸1/4跨位置横河向动应力值也较大,动应力都达到了1 MPa以上。
由于动应力数值比静应力小很多,地震作用下廊道的应力分布规律和静力条件下基本一致。动力条件下最大拉应力值为28.6 MPa,出现在右岸基岩面处廊道上游侧底部,比静应力提高了8%;最大压应力值为-39.2 MPa,发生在右岸基岩面处廊道下游侧底部,比静应力提高了6%。
4.2 典型部位应力状态
为找出廊道内部的动应力反应规律,根据廊道结构受力特点,在左岸选取了三个典型剖面(见图9(a))进行分析,动静叠加后应力分布情况如图9所示。

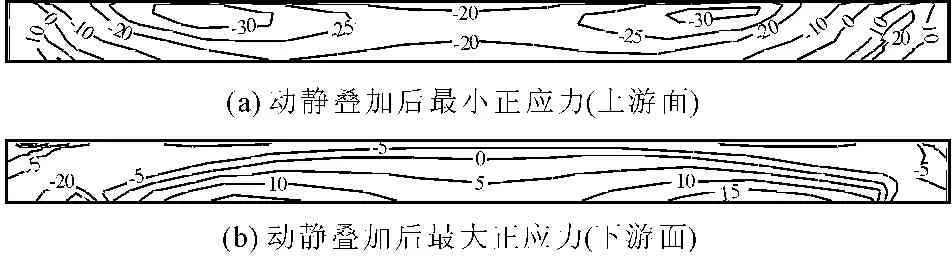
图7 横河向最大动拉应力(单位:kPa)
图8横河向正应力(单位:MPa)
地震作用下河床中央剖面,在横河向,廊道的外侧比内部动应力大,动静叠加后,拉应力极值为7.9 MPa,出现在下游面边墙外侧底部,比静力提高了14.4%,压应力极值为-22.1 MPa,出现在上游外侧边墙顶部,比静应力增大了4.2%,廊道右下侧为受拉区,左上游侧为受压区。廊道上游边墙底部及底板存在顺河向方向的拉应力,底板中央有最大拉应力5.1 MPa,比静应力增大了13.3%。廊道竖直向没有出现拉应力,在下游内侧边墙中部有最大压应力-15.8 MPa,比静应力增大了8.2%。
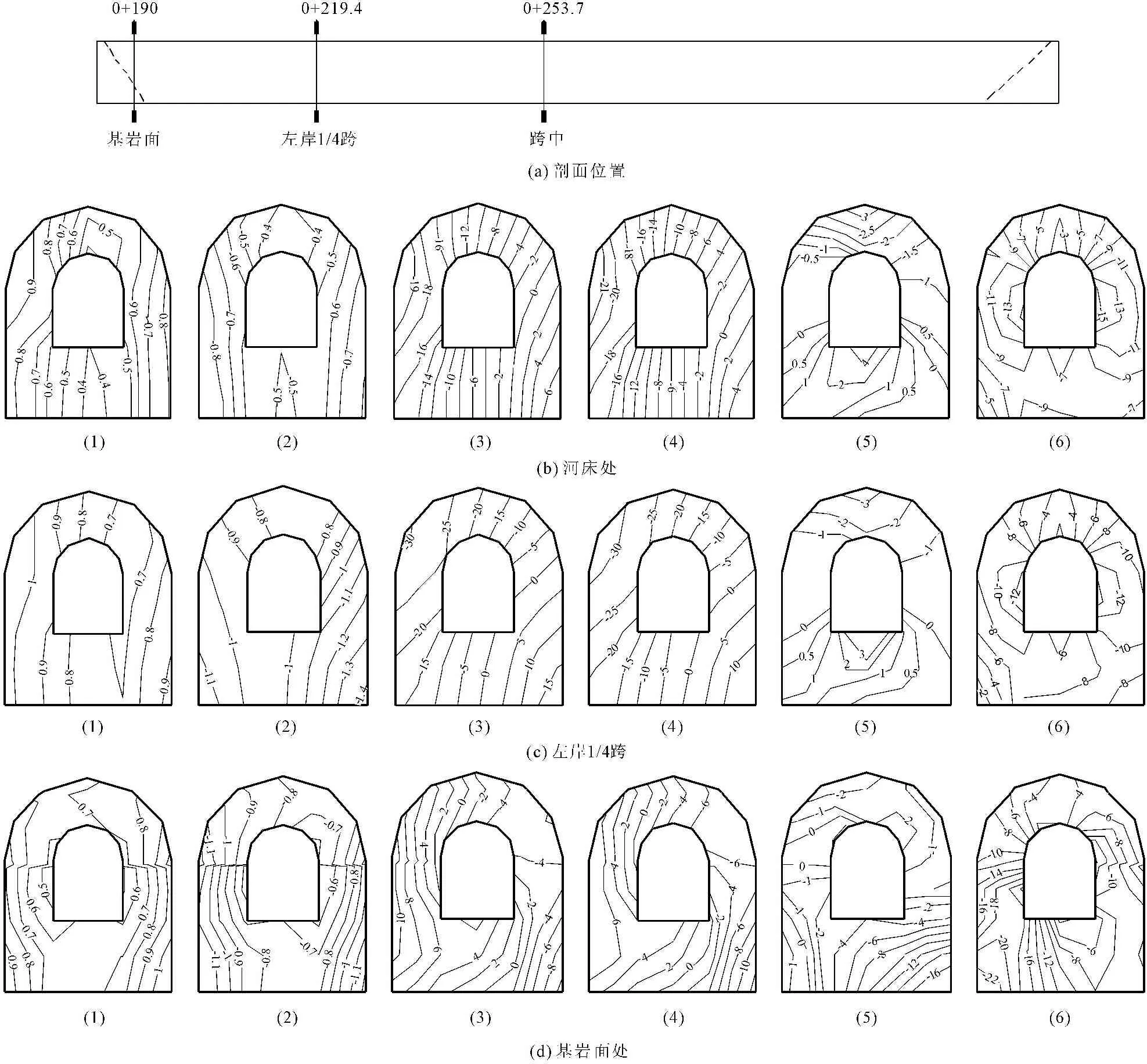
注:(1) 为横河向的动拉应力包络图;(2) 为横河向的动压应力包络图;(3) 动静叠加后横河向最大正应力包络图;(4) 为动静叠加后横河向最小正应力包络图;(5) 为动静叠加后顺河向最大正应力包络图;(6) 动静叠加后竖直向最小正应力包络图
图9廊道内部应力状态分布(单位:MPa)
左岸1/4跨剖面应力分布规律与河床中央剖面类似,横河向在下游外侧边墙底部有最大拉应力18.3 MPa,比静应力增大了6.4%,上游外侧边墙顶部有最大压应力-32.8 MPa,比静应力增大了4.4%,廊道在该位置最大动应力及动静叠加后应力均大于河床中央位置。
左岸基岩面处,在横河向,廊道拉压应力均较大,竖直向与顺河向,廊道压应力较大。
5 坝基廊道抗震安全分析
5.1 易开裂区
易开裂区为计算拉应力超过材料抗拉强度的区域,表明易开裂区如图10所示,内部易开裂区如图11所示。由于动力条件下廊道应力值较静力条件下增大在15%以内,而混凝土动强度比静强度有所提高,所以地震工况下廊道易开裂区没有显著增大。在进行廊道材料和结构设计时,只要满足其静力工况下的材料强度要求,就能保证满足设计地震工况下材料强度要求。
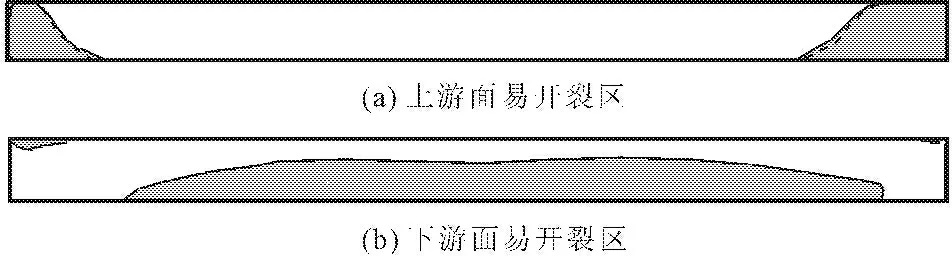
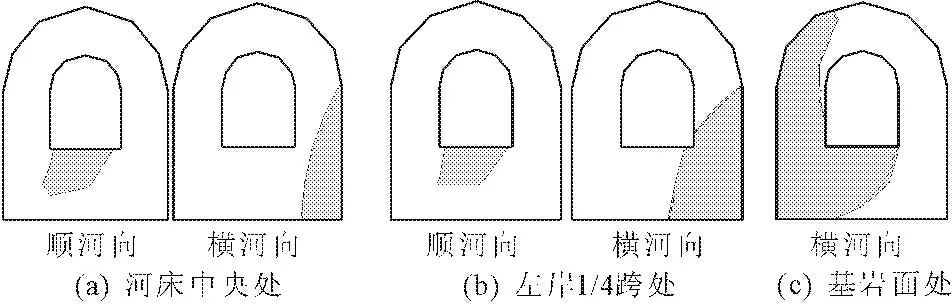
图10 横河向应力超过混凝土抗拉强度的区域(虚线为静力工况)
图11廊道内部应力超过混凝土抗拉强度的区域(虚线为静力工况)
5.2 与岸坡平硐接缝变形
瀑布沟和跷碛等已建工程,均在基覆分界位置设置了岸坡平硐与廊道的接缝,由于岸坡平硐自身变形很小,而廊道约束较弱,因此接缝处发生了较大的变形(见表2)。长河坝工程创造性地将廊道深入两岸基岩1 m,廊道与岸坡平硐的接缝变形相对已建类似工程得到有效减小,利于接缝止水的设计。动力条件下,左岸接缝最大张开比静力提高了11.4%,为4.0 cm。
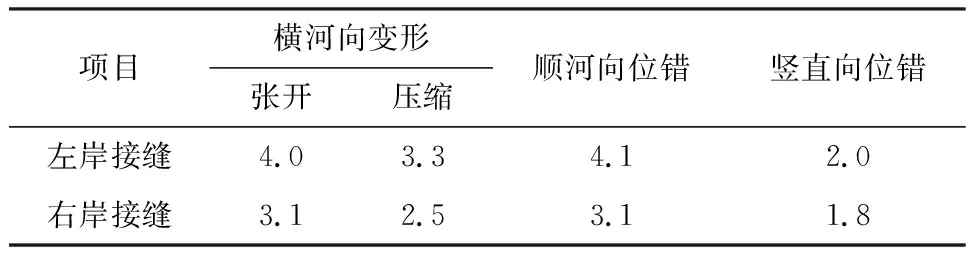
表2 廊道与岸坡平硐接缝变形单位:cm
5.3 廊道周边高塑性黏土永久变形
结合部位高塑性黏土的永久变形示意图见图12,其竖直向和顺河向的永久变形如图13所示。由于材料变形参数较低,地震后高塑性黏土主要表现为向中部的压缩变形以及向下游的变形,高塑性黏土与廊道上游面处于压紧的状态,与下游面有脱开变形趋势;与副防渗墙下游面处于压紧的状态,与上游面有脱开变形趋势。在廊道顶部靠心墙部位,高塑性黏土最大沉降变形26 cm,向上变形最大为6 cm,顺河向最大变形为15 cm左右。


图12 高塑性黏土区放大10倍的永久变形图
图13高塑性黏土区永久变形(单位:cm)
6 结 论
(1) 坝基廊道埋藏于坝体与基础内部,地震作用下动力反应较小,应力分布规律和静力工况下基本一致。高土石坝由于承受水头高,坝体变形大,廊道应力状况更为复杂。
(2) 长河坝工程动静叠加后廊道横河向最大拉应力为28.6 MPa,较静力条件下提高了8%,在廊道上游面两端,下游面河床中部有横河向较大易开裂区域。创造性地将廊道深入两岸基岩1 m,廊道与岸坡平硐的接缝变形相对已建类似工程得到有效减小,左岸接缝最大张开4.0 cm,较静力工况增大11.4%。地震后,高塑性黏土最大沉降变形值为26 cm。
(3) 地震条件下廊道的应力状况仍由静力工况控制,可借鉴深厚覆盖层地基上的马尼克3号坝经验,设置向上游拱起的廊道的轴线型式,使上游面预拉,下游面预压,从而降低横河向拉应力;由于两岸基岩面处约束较强,可将该部位廊道用钢板进行包裹。廊道与岸坡平硐接缝,建议采用伸缩节为双“U”形结构的止水并预留二期混凝土。
(4) 本文计算中将混凝土视为线弹性进行分析,计算所得基岩面处廊道上游侧底部的最大拉应力为28.6 MPa,有相当区域已远远超过混凝土的抗拉强度,因此下一步拟采用非线性模型模拟混凝土开裂破坏行为,以更加真实地反映深厚覆盖层高土石坝坝基廊道的实际工作性态。

