一种裂隙-连续介质的耦合渗流计算方法

罗璨璨，宋 俊，尚高增，杨 锦，张建海

(1.四川大学 水力学与山区河流开发保护国家重点实验室， 四川 成都 610065; 2.四川大学 水利水电学院， 四川 成都 610065)

E-mail：lccaakk@163.com

岩体中裂隙分布复杂，目前在数学上处理裂隙岩体渗流主要有：等效连续介质模型、离散裂隙网络模型和双重介质渗流模型。

等效连续介质模型是由Snow[1]提出的，Long等[2]、Oda[3]、张有天[4]、田开铭等[5-6]都对等效连续介质模型进行过研究。该模型对于解决裂隙密度较大的大尺度研究域问题有较好的效果，简单实用，能满足大多数工程的需要。

离散裂隙网络模型认为基岩为不透水介质，水流只在裂隙网络中运动，基于裂隙网络几何模型，以单裂隙立方定律为基础，各裂隙交叉点单位时间内流量平衡为准则建立方程组求解，从而确定裂隙网络中流体的真实流动状态。该模型近十几年来发展迅速，其主要研究有：Wittke[7]首先提出网络线素法，之后Wilson和Witherspoon等[8]分别采用三角形单元和线单元对二维裂隙网络进行模拟，提出了两种有限元技术；对于三维问题，Long[9]提出了三维圆盘裂隙网络模型；万力等[10]将有限元方法引入到裂隙网络渗流计算中，进一步提出了三维裂隙网络的多边形单元渗流模型。

双重介质渗流模型由前苏联学者Barenblatt G I首先提出，Warren J E等对其进一步发展。该模型可以分为两种：一是拟稳态流模型，研究代表人物有Barenblatt G I和Rott等；二是非稳态流模型，研究代表人物有Zimmerman[11]。双重介质模型有许多优点，如：在一定程度上描述了优先流现象；考虑了裂隙系统和基岩系统的水流交换，符合实际。但是该模型也有不可忽视的缺点，如：基岩被裂隙分割成具有相同的大小和形状的岩块，过于简化；物质交换系数难以确定，在应用时也需要对其有效性进行判定[12-14]。

随着对裂隙介质的深入研究，王月英等[15]提出了在研究区域上同时应用多种流动模型的耦合渗流计算方法的构想。比如ECM-DFN横向耦合模型，即某区域采用等效连续介质渗流模型，相邻区域采用离散裂隙网络模型。但文献[15]仅提出了该模型的设想，并未深入研究。张奇华等[16]深入研究了双重介质渗流模型，提出整体求解法和流量交换法两种求解方法。胡井友等[17]验证了流固耦合数值模拟的有效性。徐建国等[18]探讨了流固耦合效应对围岩稳定性的影响。

由此可知，对于既有孔隙介质，又有裂隙介质的渗流区域，目前缺乏对于相邻区域的耦合进行分析的方法。针对裂隙岩基上修筑土石坝这种特殊渗流区域，本文对岩体裂隙区域和土体孔隙区域两种不同介质分别采用裂隙渗流和连续介质渗透方法进行模拟，进而通过交界区节点水头一致性条件，对两个区域的渗流控制方程进行耦合，形成整体渗透矩阵方程，建立了裂隙-连续介质耦合渗流计算方法，并编制了裂隙-连续介质耦合渗流分析程序，开展了算例分析，印证了本文方法的正确性。

1 裂隙-连续介质耦合渗流理论及程序

1.1 裂隙渗流理论

在裂隙网络中，线单元及其两端节点为基本单元，如果节点i为线单元j的一个端点，则称j单元衔接于i节点，节点i的度数为与其相衔接的线单元的个数。构成闭合路径的裂隙段集合称为该裂隙网络的回路，其中所含裂隙段数目为回路的维数。

离散裂隙网络渗流模型认为岩块的渗透性远远小于裂隙的渗透性，可以忽略不计。水只在裂隙网络中流动。假定选取裂隙研究域ABCD如图1所示，其中有裂隙交叉点i，以i点为中心，作一通过各衔接线元中点的闭合曲线形成表征单元域。

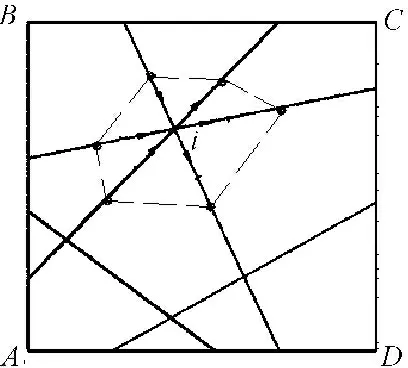
图1岩体裂隙网络示意图

根据质量守恒原理，对于稳定渗流，表征单元域内水流运动方程为：

(1)

式中：qj(j=1,2,…N′)为j线元流进或流出节点i的流量；N′为点i的度数，即交于i点的线元的总数；Qi为点i处的源汇项。

若裂隙研究区域内有N个节点(裂隙交叉点)，M个线单元(交叉点之间的裂隙段)，则可以组成N个形式为(1)的方程，写成矩阵形式为：

Aq+Q=0

(2)

式中：Q=(Q1，Q2，…，QN)T；q=(q1，q2，…，qN)T；A={aij}N×M。

A为裂隙网络中反映线元与节点衔接关系的N×M阶衔接矩阵[19]，矩阵中元素aij可表述为：

根据本文对裂隙回路的定义可知，已知裂隙研究区域内有N个节点，M个线单元，则裂隙网络中的回路个数至少为M-N+1，回路的个数与裂隙切割并围绕的岩块的个数相等。定义裂隙网络中回路矩阵C为：

C={ckj}L×M

(3)

式中：L为回路总数；ckj为矩阵C中的元素，可表述为：

回路矩阵C的方向可以提前约定，其反映了裂隙段之间的关系，有以下性质：每一行中非零元素的个数等于该行代表的回路的维数。

由衔接矩阵A与回路矩阵C的性质可证，衔接矩阵与回路矩阵正交，故有：

ACT=0或CAT=0

(4)

由上式可以得到：

ΔH=ATH

(5)

式中：H为N×1阶节点水头向量；ΔH为线元两端的水头差。

根据单裂隙内水流运动方程[11，20]，可推导单裂隙的单宽流量公式为：

(6)

流经该裂隙的水流平均速度为：

(7)

式中：Vx，Vy为流体运动速度矢量；μ为流体的动力黏滞系数；q为单宽流量；Jf为裂隙水流的水力梯度；γ为地下水的比重；b为裂隙宽度；Kf为裂隙的渗透系数。

由单裂隙渗流式(6)和式(7)可知，第j线元的流量为：

(8)

式中：bj,lj分别为线元的宽度和长度；Kf为裂隙的渗透系数；ΔHj为j线元两端的水头差。

式中裂隙段j的水力传导系数：

(9)

写成矩阵形式为：

q=Tl·ΔH

(10)

式中：

q=(q1，q2，…,qM)T； ΔH=(ΔH1，ΔH2，…,ΔHM)T；Tl=diag(Tl1，Tl2，…，TlM)

式(2)可以写成

(ATlAT)H=Q

(11)

1.2 连续介质渗流理论及程序

本文主要研究二维渗流问题，根据文献[16]，二维稳定渗流达西定律可以表达为：

(12)

式中：h=h(x,y,t)为水头函数；kx、ky为x、y方向的渗透系数。

对于未知水头值的边界Γ1，如果已知该边界上单位面积流入或流出的流量，则有流量边界条件：

(13)

式中：n为Γ1的外法线方向；q(x,y)为Γ1上的已知流量。若边界不透水，则q=0。

基于变分原理，式(12)可以等价为下列泛函取极小值：

(14)

式中：μs=ρg(α+nβ)；ρ为渗透水的密度；α为土体压缩系数；n为土体的孔隙率；β为水的压缩系数。

将渗流区域Ω离散化，剖分为m个互不相交的单元体e，单元含有M个节点，取插值函数为Ni，则单元体内任一点的水头表达式为：

(15)

依次对式(14)中各项求导并求最小值，再令所有单元的泛函的微分为0，最终将求解方程组变为：

[K]{h}={F}

(16)

式中：{F}为已知常数项；[K]表示形式如下：

(17)

整体渗透矩阵中元素和单元渗透矩阵中元素的对应关系如下：

(18)

式中：mi是共用节点i,j的单元的个数，由于每个节点的相关节点不多，因此，整体渗透矩阵是一个具有对称性的高度稀疏矩阵。

式(16)中等号右端的向量同样由单元右端向量叠加得到，单元右端向量中各元素计算公式为：

(19)

式中：w为入渗或蒸发水量；q为边界单位面积上流入的流量。

1.3 裂隙-连续介质耦合方法及程序

1.3.1 耦合原理

为了解决连续介质和裂隙介质相邻存在的区域的二维稳定渗流问题，本文建立了裂隙-连续介质渗流法，其核心为：首先分别对整个渗流分析区域内的裂隙介质系统和连续介质系统建立相应的整体渗透矩阵，然后基于两类介质共有节点的水头相等以及流量平衡原则，形成整个渗流区域的整体渗透矩阵，进行有限元分析，实际上是一种整体求解法。

由1.1节中基于图论表示的裂隙网络渗流理论可知，二维裂隙网络稳定渗流方程可写为：

[A][Tl][A]T{h}={Q}

(20)

式中：[A]为衔接矩阵；[Tl]为裂隙段水力传导系数矩阵；{h}为节点水头；{Q}为源汇项。

基于里兹有限单元法分析裂隙渗流，过程同1.2节中连续介质渗流理论，将每一条裂隙段看作一个线单元对渗流区域进行离散化，若j单元两端分别为i节点和i+1节点，则有单元渗透矩阵为：

(21)

(22)

对于j单元则有方程组为：

(23)

式中：Q和Qi+1分别为i节点和i+1节点的已知流量。

由所有的单元渗透矩阵叠加得到整体渗透矩阵为[K]，最终得到有限元方程组为：

[K]{h}={Q}

(24)

并且有：

[K]=[A][Tl][A]T

(25)

因此，在研究裂隙系统和连续介质系统横向耦合时，可以用线单元(裂隙网络中两个裂隙交叉点之间裂隙段)对裂隙介质进行离散化，用平面四边形单元对连续介质进行离散化，对所有节点进行统一编号，求得各个单元的渗透矩阵，按照节点连接关系组装在一起形成总体渗透矩阵，进行整体求解。

1.3.2 程序编制

由渗透矩阵叠加原则可以看出，整体渗透矩阵中的元素kij仅仅与i节点和j节点在含有该节点单元的局部位置有关系，与叠加时选择单元的先后顺序没有关系。因此，本文在编制程序时，首先分别对裂隙系统和孔隙系统进行整体渗透矩阵的组装，最终对所有节点进行统一编号，组装成整个渗流系统的整体渗透矩阵。

2 程序应用

2.1 工程概况

某土质心墙堆石坝，建基面高程为2 930.00 m，坝高150 m，顶宽14 m，坝体内设置黏土心墙防渗体，坡度均1∶0.25，顶宽6 m。大坝上下游坡面均在3 040.00 m高程处设4 m宽马道，上游马道以上坡比为1∶2.5，以下为1∶2.25，下游坡比均为1∶2.0。坝基以下为深度为500 m左右的深厚覆盖层，大致分为4层，在心墙底部设1.3 m厚、150 m深的混凝土防渗墙作为坝基防渗措施，插入心墙深度15 m，另在上游坝脚设置1.3 m厚、50 m深的副防渗墙，上游坝基面设水平防渗层。上游正常蓄水位3 070.00 m，对应的尾水位为2 940.00 m。

2.2 模型参数

表1中给出了该土质心墙堆石坝各个分区材料的渗透系数，本次计算采用已知水头边界，上游坝坡面按正常蓄水位施加，下游坝坡面按相应的尾水位施加。

假设坝基为裂隙岩体，其中分布着大量裂隙，采用裂隙连通路径程序进行通路搜索后，得到裂隙连通网络(见图3)。

表1 材料渗透系数

图3裂隙连通网络模型概化图

2.3 计算方案

本次计算采用表2中的6种方案，垂直防渗墙深度由150 m减小到110 m。主要计算内容有通过坝体和坝基的单宽总渗流量和主防渗墙的最大渗透比降。

表2 计算方案

2.4 结果分析

图4显示，主防渗墙深度在150 m到120 m之间变化时，流经土石坝坝基和坝体的单宽总渗流量几乎保持不变，而当主防渗墙深度减小至110 m时，单宽总渗流量从223 m3/年增长至230 m3/年，增长率为3.14%。其原因是，主防渗墙深度在120 m到150 m的这段位于岩块内部，根据图10可知，缩短过程并没有对裂隙网络造成影响；而当从120 m缩减到110 m时，本来由防渗墙阻断的两条裂隙，重新形成通路，连接到裂隙网络中，形成了新的渗流路径，导致渗流量的突然增加。由图5可见，在主防渗墙深度的减小的同时，主防渗墙的最大渗透比降基本没有变化。

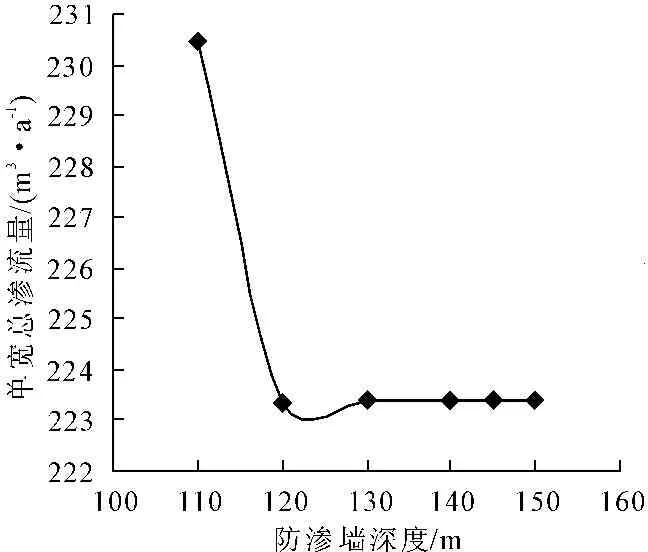
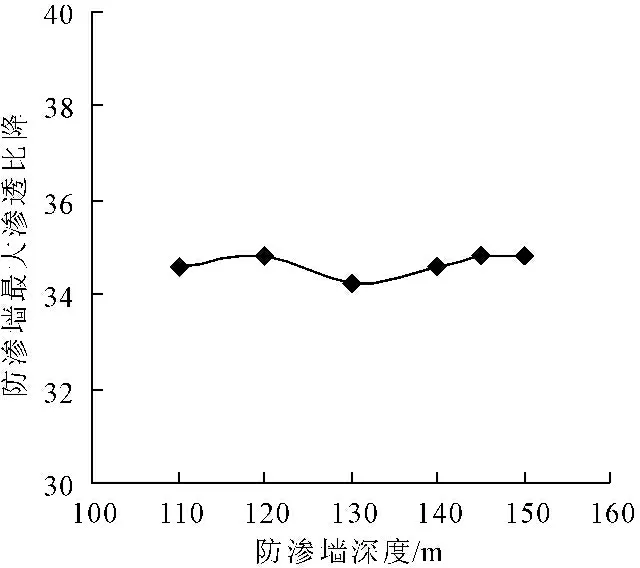
图4 单宽总渗流量随防渗墙深度的变化

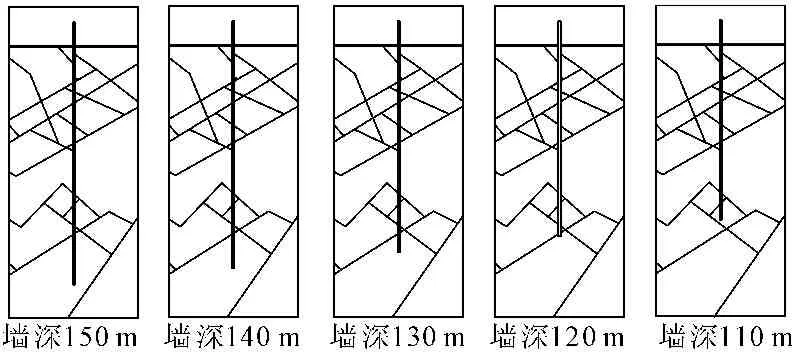
图5 防渗墙最大渗透比降随其深度变化

图6防渗墙深度从150 m到110 m变化图

3 结 论

本文针对裂隙岩基上修筑土石坝这种特殊渗流区域，根据裂隙系统与连续介质系统交界处节点水头一致的原则，将裂隙系统和连续介质系统的单元传导系数矩阵组集在一起，形成裂隙-连续介质整体耦合渗流刚度矩阵，然后对整体方程求解渗流场。编制了裂隙-连续介质耦合渗流分析程序，算例验证了程序的可靠性。

研究表明，程序可以有效描述裂隙岩体渗流特征和连续介质渗流规律，显示出良好的工程应用前景，为裂隙与连续介质的耦合渗流计算提供了新的方法。