坦克火炮身管模态分析及振动特性研究

谢 欢, 王红岩, 郝丙飞, 李善乐, 芮 强

(陆军装甲兵学院 车辆工程系，北京 100072)

坦克炮在射击时，受到外界激励的作用，火炮身管将发生弯曲变形，而炮口的振动变形将对坦克炮的射击精度产生很大影响[1].模态分析是一种研究物体固有属性的方法，通过模态分析可以得到物体的模态参数，为进一步研究火炮身管的振动特性提供基础.

针对坦克火炮身管的振动特性，李猛等[2]研究了火炮身管振动性能与射击频率的匹配关系，通过对身管模型进行模态分析，得到其固有频率和固有振型，并对模型进行谐响应分析.徐亚栋等[3]研究了复合材料火炮身管的动力学性能，在模态分析的基础上，对火炮身管进行强迫响应分析，并与金属材料的火炮身管动力学性能进行了比较.郝雷[4]对某火炮身管进行了有限元模态分析和试验模态分析，提出通过改变身管相应部位的刚度来减小其振动情况.刘雷等[5]为考虑身管的弹性变形，采用有限质量段的方法，将火炮身管离散成若干段刚体，研究了弹丸与身管的振动耦合问题.

文中针对火炮身管的振动变形特点，对坦克火炮身管进行有限元约束模态分析，并基于模态试验测试系统对其进行试验验证；根据分析结果，为提高动力学分析的计算效率，建立了火炮身管的有限段振动简化模型.

1 火炮身管有限元模态分析

坦克在越野路面上行驶时，受到复杂的外部激扰作用，底盘将产生剧烈振动，并通过悬挂装置、车体、炮塔等部件对火炮身管的振动产生影响[6].

火炮身管、炮尾和摇架连接成一体，通过炮塔上的耳轴旋转付和液压驱动机构安装在炮塔上，当坦克高速行驶时，底盘产生大幅的俯仰运动，当火炮相对坦克底盘的摆动超过最大俯仰角范围(-6°～14°),此时炮控系统液压缸闭锁，耳轴处等效为一固定端，火炮身管与底盘联结为一体.因此可将火炮身管近似简化为一悬臂梁结构，简化示意图如图1所示.

图1 火炮身管简化示意图

图1中，y为绝对坐标下火炮的振动位移;x为测量点到炮尾末端的距离;t为响应时间;xt为耳轴点到炮尾末端的距离;yt为耳轴处垂向振动位移;θ为火炮绕耳轴点的俯仰角位移.

考虑身管的弹性变形，火炮炮口的振动情况表达如下：

(1)

火炮身管是一连续弹性，理论上具有无数个自由度，具有无数阶模态，在进行模态分析时，需要考虑提取多少阶模态是足够的，针对这一问题，引入模态有效质量，用以判断系统模态的重要程度.火炮身管的振动是微幅振动，近似属于时不变定常系统，因此，根据经典模态理论，可设系统的微分方程[6]为

(2)

式中：[M1]、[C1]、[K1]分别为系统质量矩阵、阻尼矩阵、刚度矩阵；{θ1}为火炮身管的位移；{F}为激振力矩阵.

对上式进行特征值求解即可求得系统的固有频率和固有振型φ.系统广义质量矩阵定义如下:

(3)

(4)

对于第i阶模态，其模态有效质量meff,i定义如下：

(5)

所有模态有效质量之和等于结构的总质量，通过模态有效质量可以判断各阶模态的重要性.

针对图1中的悬臂梁模型，设其长度为L,单位长度上的质量为ρ，弹性模量为E,横截面积为A.则可求出前四阶模态频率和模态有效质量如表1所示.

表1 悬臂梁模态参数

从表1中可以看出，研究悬臂梁模型的振动问题，提取前五阶模态即可，并且模态阶数越低，模态有效质量越大，前两阶模态的模态有效质量占80.14%，说明这两阶模态对悬臂梁的弯曲振动贡献量最大.

查阅相关资料，火炮身管模型的几何参数、质量属性、材料属性主要参数如表2所示.

表2 身管模型结构尺寸和材料参数

根据火炮身管的主要参数，并对身管连接处的倒角、螺纹等细节特征进行简化处理，建立火炮身管的有限元模型如图2所示.根据火炮身管的约束情况，在炮尾末端和耳轴处添加固定副约束，建立约束状态下的火炮身管计算模型.

图2 身管有限元网络划分模型

火炮身管，属于基本对称结构，振动主要沿着火炮轴向的纵向振动和垂直纵向轴线的横向振动.由于火炮在射击时，炮口的振动主要集中在高低平面内，因此文中考虑的主要是火炮横向振动中的高低向振动，而不考虑水平向的振动[7].

求解得到各阶模态的频率如下表3所示，前5阶振型如图3所示.

图3 身管前五阶模态振型图

为进一步分析各阶模态的重要性，对火炮身管进行频响分析.在模型上选取典型节点位置，沿高低向施加200 N的扫频集中力，选取频带0～1 000 Hz,求解炮口振动的频率响应[7]，结果如图4所示.

表3 火炮身管前5阶固有频率和振动周期

图4 炮口振动频率响应分析

由图4分析可得，各阶模态的模态参与因子沿固有频率方向依次减小.经相关计算可知，1阶和2阶模态对炮口振动响应的贡献达85%，因此，在误差允许的范围内，3阶以上的模态振动贡献量可以忽略不计[7].

2 火炮身管模态试验验证

为了验证有限元模态分析的结果，对火炮身管进行模态试验测试.试验方法为锤击法，试验装置如图5所示，包括LMS测试系统、加速度传感器、力锤、笔记本电脑、电源等.

图5 试验装置及传感器布置

试验工况：身管热护套和排气装置拆除，炮口系统闭锁，身管轴线仰角设置在很小角度，此时身管与坦克底盘固结在一起，处于完全约束状态.

试验假设：仅考虑火炮身管的横向振动特征[8]，身管简化为悬臂梁，假设梁各截面的中心主惯性矩在同一XOY平面内，外载荷也作用在同一平面.在低频振动时，忽略剪切变形以及截面绕中心轴转动惯量的影响.

试验步骤：

(1)选取合适的测量点，对火炮身管进行取点编号；

(2)合理设置测试系统量程，调试测试仪器；

(3)由于传感器数量和仪器通道数目的限制，不能一次测得所有点的响应信号，故采用分组多次测量的方式.

(4)试验过程中，为保证测得的频响函数真实可信，应实时监测响应信号和激励信号之间的相干函数，对相干函数值低于0.9的测点需要剔除，重新进行试验.

测得典型测量点54号点的振动频响函数如图6所示.

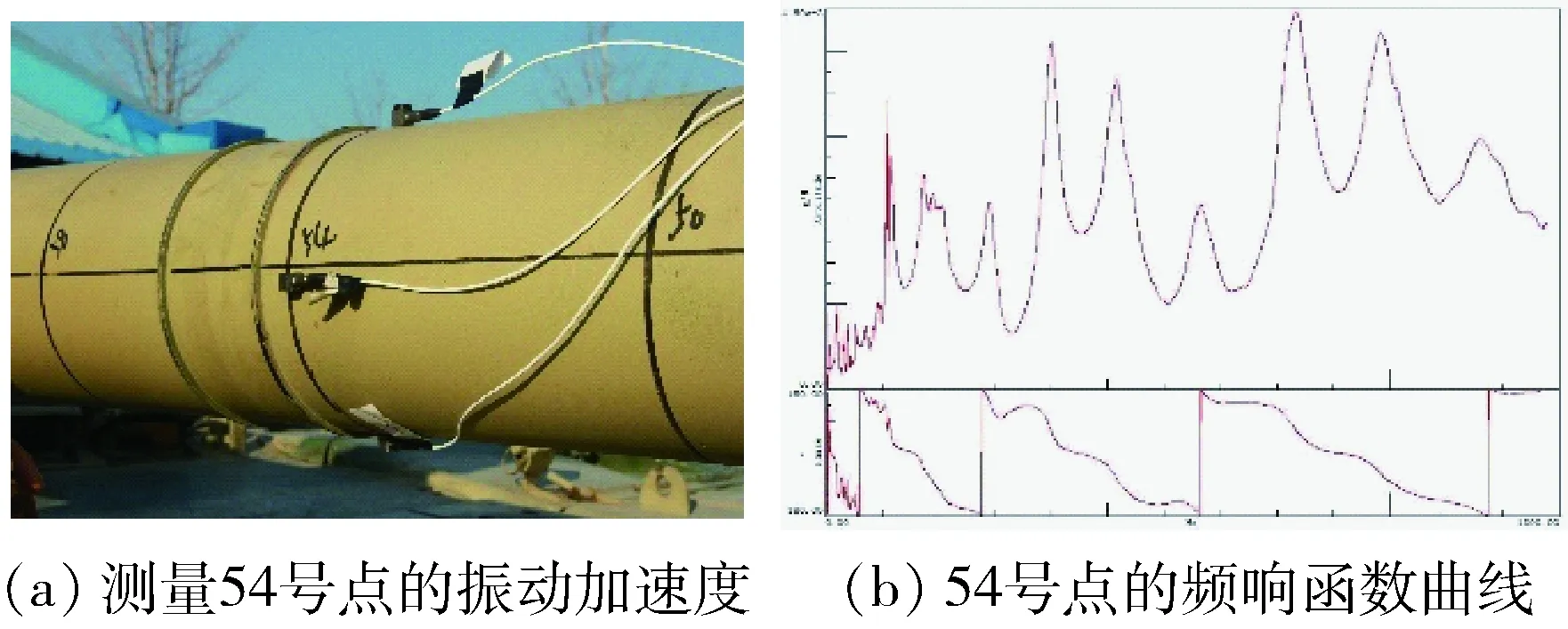
图6 54号测量点高低向振动频响函数

图7为试验模态稳定图，试验采用PolyMAX法对模态参数进行识别.PolyMAX是基于系统模态稳定图从计算得到的一组模态结果中提取所要关注的模态.

计算得到身管约束状态的前5阶固有频率和阻尼比如表4所示，前四阶振型如图8所示.

图7 试验模态稳定图

表4 身管前5阶模态频率和阻尼比

阶次模态频率(Hz)阻尼比(%)备注110.9142.73横向振动252.2304.08横向振动3144.7352.33横向振动4210.2622.97径向振动5223.5560.3横向振动

图8 前四阶模态振型图

为验证系统模态参数识别的效果，利用模态置信判据MAC矩阵进行各阶模态的相关性分析.前5阶模态的MAC矩阵如图9所示，从图中可知对角线值都接近100，非对角线值接近0，说明各阶模态振型是相互独立的.

图9 前5阶模态MAC矩阵分析图

通过模态试验得到火炮身管约束状态下的固有频率和主振型，取前3阶有限元模态频率与试验结果对比如下表5所示.

表5 模态频率计算结果对比

通过表5分析可得，有限元模态分析结果和试验模态分析结果基本吻合，误差均在10%以内，验证了所建火炮身管有限元模型的准确性.

3 建立火炮身管有限段振动模型

为了更加精确地描述火炮炮口的振动响应，刚性多体系统动力学建模理论过于简单，仅将火炮整体视为刚性体不能很好的表达炮口的振动特征，而将火炮身管考虑成柔性体，进行动力学分析时又会带来计算效率低，求解难度大的问题.因此，为解决以上问题，采用有限质量段的方法对火炮身管模型进行简化.

有限段方法是基于多刚体动力学理论发展起来的柔性体动力学研究方法，其主要思想是将连续柔性体结构件离散成有限质量段的刚体，各质量段之间通过弹簧阻尼相连，连续体的柔性特征通过等效弹簧阻尼来表征[9-10].

根据火炮身管模态分析结果，在误差允许的范围内，忽略高阶模态影响，用分段函数拟合身管归一化的2阶振型，建立火炮身管约束状态下的2阶线性振动系统模型[11].在实际工作过程中，坦克火炮身管一端悬臂，另一端和炮控系统的摇架和炮尾相连，近似为一个支撑悬臂梁结构.建立分段函数：

(6)

利用MATLAB工具箱中的Curve Fitting函数拟合归一化的阶振型如图10所示.

图10 分段函数拟合归一化的2阶振型

分段函数表达式为

(7)

通过截点位置计算火炮三段有限段模型参数包括质量、惯量、质心位置、等效弹簧阻尼特性参数.图11为火炮有限段分段结果示意图，模型分段计算结果如表6所示.

图11 火炮有限段分段结果示意图

图11中，L1为炮尾段火炮身管的长度；L2为中间段火炮身管的长度；L3为炮口段火炮身管的长度；η1为炮尾段质心到耳轴点的距离；η2为中间段质心到界面1的距离；η3为炮口段质心到界面2的距离；k12、c12分别为炮尾段与中间段之间的连接刚度和阻尼；k23、c12分别为炮口段与中间段之间的连接刚度和阻尼；m1,m2,m3分别为3个质量段的质量；J1,J2,J3分别为3个质量段绕火炮身管轴线的转动惯量.

结合所拟合的分段函数和模态振型，假设炮尾端质量段固定不动，根据所建立的三质量段火炮身管模型，对模型进行动力学分析，建立微分方程[6]：

(8)

连接处的阻尼矩阵根据经验公式计算：

[C]=β[K]，β=0.000 1. (9)

由式8计算可得，前两阶固有频率分别为10.88 Hz和52.77 Hz，与有限元前两阶固有频率比较如表7.

表7 有限元模态频率与有限段模态频率对比

从表中可知，利用有限段方法对火炮身管进行简化，建立的三质量段模型的固有特性计算结果与有限元模型差别不大，说明有限段方法应用于火炮身管是有效的，所建立的三质量段火炮身管模型为其动力学分析提供了基础.

4 结 论

文中从火炮身管的固有特性出发，将其简化为一悬臂梁模型，建立了其有限元模型，分别进行了有限元模态分析和试验模态分析，并基于模态分析结果，建立了火炮身管有限段2阶质量模型.具体结论如下：

1)根据火炮身管的实际约束状态，可将其简化为一悬臂梁模型，模态分析中前五阶模态的贡献量最大；

2)火炮身管有限元模态分析结果和试验模态分析结果相近，说明了所建立的火炮身管有限元模型的准确性；

3)火炮身管的低阶模态振动主要是横向振动，以前两阶的模态贡献率最大，根据有限段方法建立的火炮身管2阶质量模型能够较好地表征火炮身管的振动特性，为下一步仿真计算提供简化模型基础.